
Cover illustration or frontispiece: A Philosopher Lecturing on the Orrery (1766) by Joseph Wright at the Derby Museums.
This document is an HTML5 file with CANVAS tags for the diagrams. JavaScript is used for the diagrams, tables of contents, cross references, and index. If the Chrome browser fails to render a diagram, display and hide the JavaScript Console and the diagram will appear. If Firefox says “Unresponsive script”, press the Continue button.
Each diagram is
pixels wide.
Each Celx code sample is at most 80 characters wide,
with eight-character tabs.
One excerpt from
celestia.cfg in
opengl
is 94 characters wide;
a line in
Celestia:newposition
is 84 characters wide.
The above Wright painting is a 800 × 600 jpg.
The Celestia screenshot in
screenShot
is a 1024 × 790 png.
© 2013 Mark Meretzky.
All rights reserved.
Links to the Lua documentation go to
Lua version 5.2,
even though the current Celestia uses Lua 5.1.
Links to the Celx source code are provided by the gateway at
http://markmeretzky.com/cgi-bin/celx.cgi.
Links to astronomical and mathematical topics go to Wikipedia.
The HTML5 has been validated by
http://validator.w3.org/
and (with the CANVAS tags stripped out)
by
tidy.
Celestia Celestia is a computer application that displays a real-time, three-dimensional simulation of the Universe with photorealistic OpenGL graphics. When a full moon hangs over Manhattan, Celestia will render the Sun, the Moon, and New York in their actual positions and orientations. The universe can be displayed at any time and at any speed, forward, backward, or frozen. The user’s viewpoint can be fixed on the surface of a planet, mounted on a spacecraft, or piloted through the empty reaches of space. The viewpoint’s motion can be linear or curved, accelerated or constant, and accompanied by yaw, pitch, and roll.
Celestia thus combines the functionality of a camera, telescope, compass, GPS, orrery, planetarium, and starship, not to mention one of those little plastic disks with a grommet that shows you tonight’s constellations. The historically minded user can also simulate a sundial, sextant, astrolabe, armillary sphere, or a plain old noon mark.
Most people explore the Celestia universe by clicking and dragging a mouse, or, nowadays, by tapping and swiping a finger. It’s easy to go close enough to Jupiter to see the satellites, or to Saturn to see the rings. But for precise, reproducible results, far beyond those accessible to the casual user, Celestia can also be driven by a program or script.
A script can move the viewpoint to an exact position in space and time, with a precise velocity, acceleration, and orientation. We can go to Mongolia to watch a solar eclipse, or hire a jet to follow the path of totality. We can fly to the Moon with Ranger 7Ranger 7 (spacecraft)—or with George MélièsMéliès, George—and up from the Moon with Stanley KubrickKubrick, Stanley. We can observe the phases of Venus as seen from the Earth, or the phases of the Earth as seen from Mars. We can cruise alongside the Earth, keeping it stationary while the planets loop around it, or cruise alongside the CassiniCassini (spacecraft) spacecraft as HuygensHuygens (spacecraft) separates from it. And we can hold the camera steady enough to see the parallax of the star 61 Cygni.
A script can calculate an exact point in space—or in time. When is the sunset at a given date, at a given latitude and longitude on Earth? Or on the Moon, or on Mars? When are Easter and Passover, Eid al-Adha and Chinese New Year? When will Saturn’s rings be edge-on as seen from Earth? Or the orbital plane of Charon around Pluto? When will Mercury be at its next greatest elongation, and where will it appear against the background of the constellations? What will be its right ascension and declination, altitude and azimuth, and distance from the Earth? And does its perihelion really precess around the Sun as EinsteinEinstein, Albert predicted?
A script can overlay the Celestia window with OpenGL graphics. We can draw the lines on the face of a sundial, plot the equation of time, or construct the figure eight of the analemma—for any planet. We can draw on the surface of the celestial sphere, tracing the retrograde motion of Mars or the epicycles of the Ptolemaic solar system. We can draw on the surface of a planet, marking the path of an eclipse or an occultation. We can draw on the surface of the window, showing the orbital resonances of Jupiter’s moons with a corkscrew diagram. And we can draw in three-dimensional space, highlighting the Lagrangian points and equipotentials of a two-body system or building a wireframe model of Kepler’s Law of Equal Areas.
A script can search Celestia’s databases of stars and galaxies. We can plot the stars along the Main Sequence of the Hertzsprung-Russell diagram. We can see if the globular clusters are symmetrically distributed around the center of the Milky Way. We can check if the galaxies are really thicker along the supergalactic plane or thinner along the Zone of Avoidance. And we can list all the stars whose names contain the Arabic word for “tail”.
But all of these wonders are going to require programming. Celestia understands two programming languages, Cel Cel (programming language) and CelxCelx (programming language). The former is hardly a language at all, having no variables or control structure—loops, “if” statements, and functions. Celx, on the other hand, inherits these useful features from the language LuaLua (programming language), of which it is a superset. (Incidentally, the name Lua means “Moon” in Portuguese.) Celx also has classes of objects specifically for mathematics and astronomy, allowing us to harness the full power of Celestia’s simulation of the Universe with only a modest amount of coding.
The present book is a tutorial, cookbook, and reference for writing programs in the language Celx to drive Celestia. It covers the five groups of tasks that a program can do.
First, we can harvest information in numerical or graphical form from Celestia’s simulation of the universe. For example, we can ask when and where an eclipse will be total, how fast a planet will orbit the Sun, or from what angle a meteoroid stream will approach the Earth. Second, we can use this information to place the viewpoint into the simulation at a precisely computed time, place, velocity, and orientation. We can go to that eclipse and travel with it as it sweeps across the face of the Earth, or aim the camera at the radiant point of the meteor shower. Third, we can change the way the simulation is presented to the user. The window can be one large view or a splitscreen; the view can be telescopic or wide field; and the timescale can be fast forward or slow motion. The program can also overlay the window with graphics keyed to the simulated universe in the window. Fourth, we can interact with the real world. The program can read and write files, and react to keystrokes, mouse moves, or to the mere passage of real time. Finally, we can attach a Celx program to a spacecraft or planet in the simulation to pilot it on a new course. The resulting trajectory is called a “scripted orbit” or “scripted rotation”.
This book places Celx scripting squarely in the Unix tradition of making a program coöperate with its neighbors. A script is first of all a text file that can be generated by another program. The script can be launched from a command line in a shellscript or other script. It can communicate with other programs via pipes or other standard i/o, and can return an exit status to its parent. Our intent is to help users make Celx and Celestia part of a larger system involving, for example, Google Maps, a GPS or a telescope mounting, or a self-updating planetarium show. We also introduce a Standard Library for CelxCelx Standard Library, to take the rough edges off of Celx programming.
This book is addressed to the following people.
How much math do you need for this book? If you remember your high school trigonometry—sine and cosine, arcsine and arccosine—you can read more than 90% of it. See trigonometryFun for the tutorial. How much programming? If you know about variables and assignment statements, loops and “if” statements, you can read more than 90% of it. See idiosyncrasies for the tutorial. How much astronomy and navigation? If you know the difference between latitude and longitude, horizon and zenith, you can read 100% of it. See sphericalAstronomy for the tutorial.
Reasoning in three dimensions takes practice. A desktop celestial sphere will aid the reader in visualizing the equinoxes, solstices, and the other cardinal directions in the many frames of reference offered by Celestia. If no sphere is available, get an orange and draw on it with a magic marker or stick pins into it. A conventional globe of the Earth will be helpful in seeing where the axes and other vectors pierce the terrestrial surface. The author always carries in his pocket a cheap little painted tin globe with a pencil sharpener in its base.
Celestia is free and runs on Macintosh macOS, Microsoft Windows, and Linux. It is open source and can be ported to any platform that has the languages C and C++ and the graphics library OpenGL. An enthusiastic user community has extended Celestia with additional planets and spacecraft (real and imagined), and surface imagery with new layers of information. But libraries of Celx functions and programs are coming more slowly, which is one of the reasons for this book.
The Celx viewpoint or camera is called the observerobserver (viewpoint), and is referred to herein as “he” only for convenience. I am grateful to the creators of Lua and Celestia, to Harald Schmidt Schmidt, Harald (documenter) for his pioneering Celx documentation, and to Marc Taylor Taylor, Marc (planetarium operator) for introducing me to the Celestia universe.
Mark Meretzkymark.meretzky@nyu.edu
http://markmeretzky.com/
This section lists the rules we obey, voluntarily or otherwise, when writing programs in Celx. You can skip it on first reading.
This book describes version 1.6.1 of Celestia, which implements a Celx language that is a superset of version 5.1.4 of LuaLua (programming language). Since the current version of Lua is already 5.2.2, we will be forced to write obsolete or deprecated code in a few places. See lua52 for the list of things to be changed in our Celx code when Celestia is upgraded to Lua 5.2.
For your version numbers of Lua, Celestia, and the Celx Standard Library,
see the Lua variable
_VERSION
and the standard library variables
std.celestiaVersion
and
std.libraryVersion.
The
Celestia:geturlCelestia:geturl
method of
Celestia version 1.6.1 returns a
cel:cel: URL
URLURL (Uniform Resource Locator)
containing a version number of 3.
All earlier versions of Celestia generated a URL with no version number at all.
We will occasionally glance at the source code of Celestia and Lua.
The Celestia source resides in a tree of directories whose root is named
version.
We will cite the files starting at this root.
The Lua source is rooted at
luaversion.
The data files read by Celestia at runtime are in the
Celx directory
(celxDirectory)
and its subdirectories:
data,
extras-standard,
fonts,
and
textures.
The Celestia source code is mostly in the language
C++C++ (programming language).
The
.m
files are in
Objective-CObjective-C (programming language)
for Macintosh,
and the
.mm
files are a mixture of Objective-C and C++.
The Lua source code is in the language
CC (programming language).
Our convention in this book is to give lowercase names
to Celx variables and functions.
This includes variables that hold a constant value,
in agreement with the Lua constant
math.pi.
A name can be formed by concatenating two or more words. Celx already has three conflicting conventions for pasting them together.
tostring
and
tonumber,
the Celx methods
Celestia:getobserver
and
Celestia:newposition,
and the field
renderoverlay
in the Lua hook table in
luaHookFunctions.
(A “method” is a certain type of function; see
objectsAndClasses.)
KM_PER_MICROLY
(lightyear)
and the Celx functions
celestia_cleanup_callback
and
celestia_keyboard_callback
(callback).
atmosphereHeight
in the Celx info table
(infoTable)
and the field
initialOrientation
in the
Observer:goto
table.
Our convention in this book is to use concatenation in all lowercase for the names of methods; see objectsAndClasses. This agrees with the existing Celx convention for methods. We use concatenation with embedded capitals for the names of other functions and variables.
We place “longitude” before “latitude”
in the names we invent,
to agree with the Celx function
Observer:gotolonglat.
Examples include
Celestia:newpositionlonglat
and
Vector:getlonglat.
What is the opposite of “end”?
Celx uses both
“start”
and “begin”.
For example, the
Observer:goto
table contains the fields
startInterpolation
and
endInterpolation
(animateRotation),
while the table returned by a scripted orbit function contains the fields
beginDate
and
endDate
(Geostationary).
Our convention is to use
“start”
because it has fewer syllables.
Some Celx methods return a Lua table,
such as
Celestia:tdbtoutc
and
Celestia:fromjulianday.
Others return a list of values,
such as
Celestia:getscreendimension
and
Phase:timespan.
Most of the methods we invent return tables;
examples include
Position:getlonglat,
Vector:getlonglat,
etc.
Exceptions are
Position:getxyz
and
Vector:getxyz,
whose purpose is to return an argument list for the Lua function
string.format,
and
std.tourl,
which return the argument list for the method
Celestia:newposition.
Another exception is
Object:family,
which is required to return a list by the semantics of the Lua
generic
for
statement.
Finally,
Rotation:getforwardup
proved easier to use when it returned a list.
Every complete Celx program is printed in a solid box, adorned with a link to the source code online. A Celx code fragment is printed in a dashed box. Output is in a double box.
Note that “complete” is a relative term.
If the program has the following
require
statement,
--This is a Celx code fragment.
require("std")
the program will need the file
std.luastd.lua (file)
in order to run.
This file contains the
Celx Standard Library
(standard)
and is printed in full in
stdCelx.
Some programs will also need a
Lua hook
file
(luaHookFunctions)
or files containing
scripted orbitsscripted orbit
and/or
rotationsscripted rotation
(scriptedOrbit).
Our Celx code is written in the plain vanilla ASCII character set, with a maximum line length of 80 characters and 8-character tab stops. But these restrictions are not required by Celestia. We obey them only to make the code readable on every platform.
Despite being written in ASCII, many of our programs output non-ASCII characters. Examples include the symbols for degree, minute, and second (1° 2′ 3″). These “special” characters are encoded in the UTF-8UTF-8 (character encoding) format.
Let’s play with Celestia interactively before we start writing programs.
Download Celestia from
http://www.shatters.net/celestia/
The Macintosh macOS and Microsoft Windows versions install unproblematically. During the Windows installation, under “Select Additional Tasks”, check the checkbox for “Associate .cel and .celx scripts”. On Linux, download the Celestia package for your distribution. Do not download the “Linux (x86) Version 1.4.1” from the downloads page on the Celestia website—this version cannot run Celx programs.
At a much later stage, you might want to compile your own Celestia from its source code. See compileMacintosh for Macintosh macOS, compileWindows for Microsoft Windows, compileLinux for a Linux version of Unix, and solaris for the Solaris version.
On startup,
Celestia automatically runs an eight-second program named
start.celstart.cel (Cel program).
It whisks us safely away from the Sun and
leaves us above the sunlit side of the Earth
with the message “Welcome to Celestia!”.
To immerse yourself in the Celestia universe,
you can then maximize the Celestia window.
Another program is
demo.celdemo.cel (Cel program),
a four-minute tour of the Celestia universe.
Pull down the
Celestia
menu on Mac,
or the
Help
menu on Microsoft Windows,
and select
Run Demo.
When done,
it leaves us back at the Earth with the message
“Demo completed.”
These programs are not hardwired into Celestia.
They are specified in the configuration file
celestia.cfgcelestia.cfg (configuration file):
To find the “Celx directory”Celx directory that holds the configuration file and the programs, see celxDirectory.
This section demonstrates some of Celestia’s
interactive commandskeystroke commands.
It previews the features
that will be invoked non-interactively by the Celx programs later in the book.
For the complete list of interactive commands,
pull down Celestia’s
Help
menu and select
Celestia Help
on Mac,
Controls
on Microsoft Windows.
start.cel
places him six Earth radii from the center of the Earth,
facing the sunlit side of the planet.
To rotate him around the Earth,
you can then drag the mouse across the planet.
On Mac, you right-drag or option-drag;
on Microsoft Windows, you right-drag.
You can also rotate him
by holding down the shift key and pressing the four arrow keys.
To roll the observer,
press the left and right arrows without shifting.
Visit Europe, Australia, and the North and South Poles.
return
on Mac,
Enter
on Microsoft Windows,
to get the prompt
Target name:.
Then type
Earth
and press
return
or
Enter.
The Earth is now selected.
Press c to center the selected object in your field of view,
and g to go there.
Press
HomeHome key
and
EndEnd key
to go towards and away from the selected object.
If your keyboard has no
Home
and
End,
you can drag up and down to get the same effect:
command drag on Mac,
left drag on Microsoft Windows.
End
and
Home
to withdraw from the Earth until it just barely covers the Sun.
We have just traveled to the vertex (tip) of the Earth’s
umbraumbra (of Earth).
We can withdraw further to make an
annular
eclipseannular eclipse.End
to get farther from the Earth so it blocks less of the sky.
Sol/slash (in name of celestial object)Earth
with a diagonal slash.
Or simply press
h
h (home command)
(home) to select the Sun,
and g to go to it.
~~ (toggle console comand)
(tilde).
Scroll it up and down with the arrow keys.
How many stars are in the binary database?
On startup, the observer is
deposited by
start.cel
at a position
six Earth radii from the center of the Earth,
or five radii from the surface.
The
trig
trigonometry
function
sinesine (trig function),
as we all remember,
is “opposite over hypotenuse”.
Conversely,
arcsinarcsine (trig function)
1
6
is the angle whose sine is 1/6.
This is the angle subtended (spanned)
by half of the Earth from the observer’s point of view.
The whole Earth subtends an angle twice as wide:
2 arcsin
1
6
The angle returned by the Lua arcsine function is in
radiansradian.
To convert it to degrees,
we multiply by
180/π.
The Earth therefore subtends an angle of
180
π
2 arcsin
1
6
degrees from the observer’s point of view,
approximately
19.1881364537209°.
(We write our numbers with 15 significant digits; see
doubleArithmetic.)
Each degree consists of 60 minutes of arc,
and each minute consists of 60 seconds.
We can therefore write the angle as
19° 11′ 17.2912333953224″
Does this agree with the Earth’s
“Apparent diameter”
apparent diameter
in the upper left corner of the window?
Given this apparent diameter of 19.1881364537209° ≈ 19° 11′ 17.2912333953224″ we can reconstruct the observer’s distance in Earth radii from the center of the Earth. Half of the apparent diameter is 19.1881364537209 2 degrees. The sine of this angle is “opposite over hypotenuse”, i.e., the Earth’s radius over the observer’s distance from the center of the Earth. The argument of the Lua sine function is in radians, so we convert the angle to radians by multiplying by π/180. The sine is sin ( π 180 19.1881364537209 2) ≈ .166666666666667 ≈ 1 6 Therefore the observer is 6 radii from the center, or 5 radii from the surface. Does the latter figure agree with the Earth’s distance and radius in the upper left corner of the window?
The Earth’s limblimb is the apparent edge of the Earth as seen by an observer. It is the circle where the surface of the Earth meets the background of space. (If we were much closer to the Earth, we would call it the horizonhorizon.) The observer is 6 Earth radii from the center of the Earth. How far is he from any point on the Earth’s limb? The middle diagram above suggest that the distance should be slightly less than 6 radii.
This is a job for the trig function tangenttangent (trig function), also known as “opposite over adjacent”.
tan ( π 180 19.1881364537209 2 ) ≈ 0.169030850945703 ≈ 1 5.91607978309962The observer is therefore approximately 5.9 Earth radii from the limb.
The field of view field of view is the angle subtended by the height of picture in the Celestia window. It does not include the title bar and the horizontal scroll bar. The angle is displayed in degrees as the “FOV” in the lower right corner.
Look at the Earth and select it to display its apparent diameter. Then drag on the lower right corner of the window and shorten it until it is just barely tall enough to contain the Earth. Has the field of view become equal to the Earth’s apparent diameter?
Select the Moon and press
g
to go there.
You are now five Moon radii from the center of the Moon,
a distance set by the function
getPreferredDistance
in the file
version/src/celengine/observer.cpp.
At this distance,
the Moon should subtend an angle of
180
π
2 arcsin
1
5
degrees, approximately
23° 4′ 26.1050362715114″.
Does it?
Let’s write a “Hello, World!” program“Hello, World!” program in Celx, save it on the disk, and run it.
Before we write the program,
we have to decide what directory to put it in.
We will choose the directory that makes it easiest
to run the program by typing an operating system command line.
This directory is called the
Celx directory
and it already holds the configuration file
celestia.cfgcelestia.cfg (configuration file)
and the programs
start.cel
and
demo.cel
that we ran in
play.
It will also hold the Celx Standard Library file
std.luastd.lua (file)
(standard),
the Lua hook file
luahook.celx
(luaHookFunctions),
and the files for scripted orbits and rotations
(scriptedOrbit).
Although the Celx directory is in a different location on each platform,
we can always find it by searching for the file
start.cel.
To get to the Celx directory on a Mac,
start with the application
Celestia.app.
A Mac application is actually a
“package”package (Macintosh)
of directories and files.
(“Directory” and “folder” are synonymous on Mac.)
The root directory of this package is named
Celestia.app.
The Celx directory is a
sub-sub-sub directory named
CelestiaResourcesCelestiaResources (Macintosh directory).
To get there,
Celestia
volume you downloaded.Celestia.app
and select
Show Package Contents.Contents
and
Resources
to
CelestiaResources.
When you get to the Celx directory,
you should see the files
celestia.cfg,
start.cel,
and
demo.cel.
To go to the Celx directory in the
Terminal
application,
give the following commands.
The entire
Celestia
volume is read-only.
To store a program in the Celx directory,
you must give yourself read and write privileges for that volume.
Control-click on the icon for the
Celestia
volume, select
Get Info,
and open
Sharing & Permissions.
If you have no permission to change the permissions,
a workaround is to create a read/write copy of
Celestia.app.
Double-click on the
Celestia
volume,
control-click on
Celestia.app,
and select
Copy "Celestia.app".
Then control-click on a new location (your desktop,
or the
Applications
folder in the
Macintosh
HD)
and select
Paste Item
to create a new
Celestia.app.
From now on, our Celx directory will be the
CelestiaResources
sub-sub-sub directory of the new
Celestia.app.
For example, if we pasted the new
Celestia.app
onto our desktop,
we can get to the Celx directory with the following Terminal command.
cd /Users/Yourname/Desktop/Celestia.app/Contents/Resources/CelestiaResources
The Celestia Setup Wizard tells us the name of the Celx directory
during installation.
It defaults to a directory such as one of the following.
C:\Users\Myname\AppData\Local\Celestia
Go to the directory and look for the files
C:\Program Files (x86)\Celestia
C:\Program Files\Celestiacelestia.cfg,
start.cel,
and
demo.cel.
If you don’t see the filename extensions
(.cfg
and
.cel)
in the directory,
go to
Start →
Control Panel →
Appearance and Personalization →
Folder Options →
View →
Advanced settings
and uncheck
“Hide extensions for known file types”.
Press Apply and OK.
Another way to get to the Celx directory is
to open the Command Prompt window by running
cmd.exe.
Then give the following commands.
cd C:\Users\Myname\AppData\Local\Celestia (or whichever directory it is)
dir celestia.cfg start.cel demo.cel
The Celx directory defaults to
/usr/local/share/celestia.
A different default can be set by passing the command line options
--prefix=PREFIX
and
--datarootdir=DIR
to the
configureconfigure (shellscript)
shellscript that is run before Celestia is compiled.
For help with these options,
download the Celestia source code and say
cd version
./configure --help | more
If you don’t know where the Celx directory is,
find it by searching for the file
start.cel
with the following command.
Discard any error messages by directing them into the garbage pail
/dev/null.
There is no space between the
2
and the
>.
find / -type f -name start.cel -print 2> /dev/null
Now that you know where your Celx directory is,
go there and read
start.cel
and
demo.cel.
start.cel,
select
Open With,
and choose an editor such as
TextEdit.appTextEdit.app (Macintosh text editor).
start.cel,
select
Open With…,
and choose an editor such as
WordPadWordPad (Windows text editor)
or
NotepadNotepad (Windows text editor).
Terminal,
open
start.cel
with a text editor such as
vivi (Unix text editor),
vimvim (Unix text editor),
emacsemacs (Unix text editor),
or
picopico (unix text editor).
I use
vi;
my children use
pico.
Observe that CelCel (programming language) is an impoverished language. It has no variables or objects, only literal numbers and strings. It also has no control structure—no loops, “if” statements, or functions. That’s why we’re going to program in Celx.
“What?” exclaimed the general and the major, a bit taken aback by this idea.
“Absolutely,” replied BarbicaneBarbicane, Impey with self-assurance. “Absolutely. Otherwise our experiment would produce no result.”Our first Celx program will have to perform some kind of output, to prove to us that it actually ran. Otherwise our experiment would produce no result.
Go to the Celx directory
(celxDirectory)
and launch any text editor capable of creating a plain text file.
It can be the text editor with which you examined
start.cel
in the above exercise.
Write your program in a text file named
hello.celx
(or
hello.clx,
if you find it important to have a filename extension of
exactly three characters).
We will draw a solid box around each program.
Commentscomment
start with a double dash,
implying that Celx does not have the decrement operator
“--”
used in the language C.
A double-dash comment extends to the end of the line.
A double-dash comment with double square brackets
can extend onto additional lines.
Don’t forget the closing brackets.
Do not confuse the lowercase letter
o
with the digit
0,
or the lowercase letter
l
with the digit
1.
For example, the filename extension
.celx
has a lowercase
l.
Do not confuse the dash
-
with the underscore
_,
or the
(parentheses)
with the
[square brackets]
and
{curly braces}.
--[[
This file is named hello.celx.
Keep the Sun reassuringly in view,
but position the observer away from its glare.
]]
observer = celestia:getobserver()
position = celestia:newposition(0, 0, 1) --x, y, z coordinates
observer:setposition(position)
celestia:print("Hello, world!", 10) --for 10 seconds
wait() --Give Celestia a chance to update the window.
--[[
Celestia keeps running after the Celx program has finished.
The variables observer and position, and the objects to which they refer,
continue to exist and can be mentioned by subsequent Celx programs.
The text "Hello, world!" remains in the window even after the program
has finished.
]]
Save the file as plain text,
since rich text would make Celestia complain
about an invisible “curly brace in line 1”.
In Mac
TextEditTextEdit.app (Macintosh text editor),
pull down the Format menu
and select
Make Plain Text.
In Microsoft
WordPadWordPad (Windows text editor),
select
Save as → Plain text document
Save as type: TextDocument
When the program is run in
launch,
the output of
Celestia:print
(celestiaPrint)
will be white on black.
But we will just give it a double border to save ink.
Hello, world!
Let’s examine the objects and methods of the program in programItself. An objectobject (in programming language) is something that does useful jobs for us. There are many classes of objectsclass (of object), including the twelve classes that Celx has added to Lua (listed in additions). The name of each of these classes starts with an uppercase letter.
One class of object is named
CelestiaCelestia (class).
This class is unusual in that there is always exactly one object of this class
(at least until we get to
luaHookFunctions).
We don’t have to create or destroy this object:
it always exists.
The object of class
Celestia
is named
celestiacelestia (object),
with a lowercase c.
The other two objects,
observer
and
position,
are created by the program.
They belong to classes
ObserverObserver (class)
and
PositionPosition (class)
respectively.
But the name of an object does not necessarily have to be
the name of its class in lowercase.
Just choose a name that reminds you of what the object does.
The jobs that an object can do are called the
methodsmethod
of the object.
An object of class
Celestia
has methods named
getobserver,
newposition,
and
print.
The methods of the objects of each class are listed in
additions.
To tell an object to
call
(perform) one of its methods,
we write the name of the object on the left
and the name of its method on the right,
joined by a colon.
We also write a pair of parentheses after the name of the method.
Thus,
A method can access whatever data might be in the object to which it belongs.
For example, the
getobserver
method of the
celestia
object can access the data in the
celestia
object.
In addition,
some methods must be fed additional data
such as the three numbers we passed to
newposition.
These values are called the
argumentsargument (of method)
of the method
and are written inside the parentheses.
Even if there are no arguments,
the parentheses are still required.
Multiple arguments are separated by commas.
A method can produce an object or other value
as the result of its work.
This value is called the
return valuereturn value (of method)
of the method.
For example,
the
getobserver
method of the object of class
Celestia
(known henceforth as
Celestia:getobserver)
gets an object of class
Observer
and returns it to us.
An
Observer
object represents a point of view in the simulated universe.
It has a position, orientation, and velocity.
The observer’s initial position is at the
barycenterbarycenter (of Solar System)
of the
Solar System,
always in or near the
Sun.
We also receive a return value from
Celestia:newposition,
in this case an object of class
Position.
The new position was chosen
to keep the Sun reassuringly in view—at a respectful distance.
The three coördinates of this position are explained in
universalFrame.
Some methods produce no return value.
Observer:setposition
moves the observer to a new position,
but returns no value.
Celestia:print
displays text in the window,
but returns no value.
See
celestiaPrint
for the arguments of
Celestia:print.
When Celestia is launched without specifying any Celx program,
the program
start.celstart.cel (Cel program)
(programs)
automatically whisks the observer to a safe distance from the barycenter.
But when we launch Celestia by launching a Celx program,
start.cel
is not executed
and the Celx program must get the observer away from the barycenter.
This is an important responsibility.
If we remain too close to the Sun, the
glare
will be blinding.
Even worse,
if we are inside the Sun,
the Sun will be invisible and the user will be disoriented.
A method that does not belong to any object is called a
functionfunction.
For example, the function
waitwait
gives Celestia an opportunity to update its window.
See
wait.
We can launch our program
hello.celx
in three ways.
The third way must be used if the Celx program produces
“standard output”
(standardOutput).
start.cel.
Then pull down Celestia’s
File
menu,
select
Run Script…,
and choose
hello.celx.
This will execute
hello.celx
without executing
start.cel
a second time.
hello.celx.
This will launch Celestia without executing
start.cel.
Celestia will then execute
hello.celx.
start.cel.
Celestia will then execute
hello.celx.
Details about launching on the three major platforms are in the following subsections.
There is no way to pass command line arguments to a Celx program.
A Celx program inherits many values from the previous Celx program(s)
run by the same instance of Celestia.
These values include the observer object,
the renderflags
(renderFlags),
the nonlocal variables
referring to objects and functions
(functions),
the permissions to access the local file system and operating system
via the Lua variables
io
and
os
(osExit),
and even the six-digit
screenshotCount
(screenShot).
The simplest way to discard this baggage and guarantee a clean start
is to quit Celestia and launch it again.
For now, don’t worry about it.
A running Celx program can be pausedpause and unpaused with the space bar, and cancelledcancel (terminated) with the escape key. But the escape key does not cancel an event handler function (eventHandler) or a Lua hook function (luaHookFunctions).
The program we’re about to launch
contains Celx code that will execute once and then come to an end.
Later, we will see other ways of submitting Celx code to Celestia:
as a Lua hook
(opengl),
a scripted orbit or rotation
(scriptedOrbit),
or a file that is
required
(standard)
by any of the above.
A Celx program can also run a Celx program in another file by calling
the method
Celestia:runscript,
or a Celx program in a string by calling the Lua function
loadstring.
One piece of trivia.
On each platform, the name of the Celx program must be
specified with at least one
slashslash (in filename)
if the program calls the methods
Celestia:loadtexture
or
Celestia:runscript.
For example, the name would have to be specified as
./hello.celx
or
/pathname/of/hello.celx
instead of
hello.celx.
1.
Launch Celestia, pull down the File menu,
and select
Run Script….
Observe that the resulting menu does not let us drill down
into
Celestia.app,
making it impossible to reach the Celx directory
CelestiaResources
and run
hello.celx.
The solution is to move
hello.celx
into the
scripts
subdirectory of the Celx directory.
We can then get to it by selecting
File → Scripts.
2.
We can also run
hello.celx
by double-clicking on the its icon in the Macintosh Finder.
If the double click does not launch Celestia,
make sure you have chosen Celestia as the application for opening
.celx
files.
Control-click on
hello.celx,
select
Open With,
choose
Celestia,
and check
“Always Open With”.
3.
We can also run
hello.celx
by typing a command line in the Terminal application.
The command line will launch
the executable file
Celestia,
which will then execute
hello.celx.
To make it easy to launch the executable
Celestia,
take the name of the directory that holds
Celestia
and append it to the
PATH
environment variable.
You can accomplish this automatically every time you open a Terminal window
by putting the following command
into the
.bash_profile.bash_profile (shellscript)
file in your home directory.
~ (home directory)/.bash_profile file.
#Assumes you have copied your Celestia.app onto your Desktop.
export PATH=$PATH:~/Desktop/Celestia.app/Contents/MacOS
Now close and reopen the Terminal window and type the following commands into it.
echo $PATH which Celestia /Users/myname/Desktop/Celestia.app/Contents/MacOS/Celestia
If no directory name is specified for
hello.celx,
Celestia will look for it in the Celx directory.
In the jargon of operating systems,
a pathname passed to Celestia
is “relative to” the Celx directory.
The Celx program can be run again by typing
command-r
into Celestia.
There is no need to make the Celx program “executable” with
chmod,
but see
pound,
which offers an easier way to run the program.
1.
Launch Celestia and pull down the File menu.
Select
Open Script…
and choose your program
hello.celx.
2.
We can also run
hello.celx
by double-clicking on its operating system icon.
If the double click does not launch Celestia,
make sure you have chosen Celestia as the application for opening
.celx
files.
Right-click on
hello.celx,
select
Open With →
Choose Program…,
choose
Celestia,
and check
“Always use the selected program to open this kind of file”.
3.
We can also run
hello.celx
by opening the Command Prompt window
and type one of the following commands.
(Launch
cmd.exe to open the window.)
If no directory name is specified for
hello.celx,
Celestia will look for it in the Celx directory.
In the jargon of operating systems,
a pathname passed to Celestia
is “relative to” the Celx directory.
The above commands should launch Celestia because we said
“Associate .cel and .celx scripts”
when we installed Celestia.
If Celestia doesn’t launch,
we will have to tell the computer that
a
.celx
program should be executed by Celestia.
On Windows 7,
Start →
Control Panel →
Programs →
Default Programs →
Associate a file type or protocol with a program
The extension
.celx
should be listed.
If it isn’t,
make it open with
Celestia.
On Windows XP,
Start →
My Computer →
Tools →
Folder Options… →
File Types
If
CELX
is not listed under
Extensions,
right-click on
hello.celx and
select
Open.
Press “Select the program from a list”,
press OK,
and browse to Celestia.
Check “Always use the selected program
to open this kind of file”.
On Windows Vista,
Start →
Control Panel →
Programs →
Default Programs →
Make a file type always open in a specific program
The extension
.celx
should be listed.
If it isn’t,
make it open with
Celestia.
Do not install the outmoded Linux version 1.4.1 in the Celestia
download page:
it rejects a
.celx
file as an
“Invalid filetype”.
To run Celx on Linux,
get a fresh Celestia from your Linux distribution
or go to
compileLinux
and compile Celestia from the source code.
If no directory name is specified for
hello.celx,
Celestia will look for it in the Celx directory.
In the jargon of operating systems,
we say that a pathname passed to Celestia
is “relative to” the Celx directory.
The
-f
in front of
hello.celx
is necessary only if Celestia was compiled with the
--with-glutGLUT (OpenGL Utility Toolkit)
option of the
configureconfigure (shellscript)
shellscript.
It is not necessary if Celestia was compiled with the
--with-gnome,
--with-gtk,
or
--with-kde
options.
One exception:
if Celestia was compiled
--with-kdeKDE (K Desktop Environment),
the pathname of the
Celx program is relative to the user’s
current
directory,
not the Celx directory.
The location of the Celx program affects the arguments of the Celx methods
Celestia:loadtexture
and
Celestia:runscript.
To launch Celestia or any Celx program on my
Solaris Unix server,
I first have to connect to the server
by launching an
X WindowX Window
server on a Mac or Microsoft Windows.
On a Mac,
I launch
X11.app
and log into the Unix server with
sshssh -Y.
On Microsoft Windows,
I launch
XmingXming
and log into the Unix server with
PuTTYPuTTY
set to
“Enable X11 Forwarding”.
Look under
PuTTY Configuration →
Category →
Connection →
SSH →
X11 or Tunnels.
See
pound
to make the
.celx
file executable.
Every language has its own features. Some of the distinguishing marks of Celx were inherited from Lua; others were introduced by Celestia.
Since the
celestia
object is heavily used in Celx,
we could have given it a shorter name.
The following code is a Celx fragment,
not a complete program,
so we’ll put a dashed box around it.
c = celestia
observer = c:getobserver()
observer = c:newposition(0, 0, 1)
The
object of class
Celestia
is unaware that it now has an extra name.
In fact, it never knew that it had the name
celestia.
c
and
celestia
are actually the names of little containers called
variablesvariable,
completely external to the object.
Each variable contains the memory address of an object,
by means of which the computer can find its way to the object.
The memory address is therefore called a
referencereference to object
to the object,
and a variable that contains a reference is said to
refer
to the object.
In our example,
the variables
c
and
celestia
refer to the same object.
For convenience,
we will continue to speak of
“the celestia object”,
but what we really mean is
“the object referred to by the variable named
celestia”.
A variable is not an object
and does not contain an object.
Our assignment statement
c = celestia
copies the content of the variable
celestia
into the variable named
observer.
But this content is merely a reference to an object.
The statement does
not
copy the object itself.
Remember, there is only one object of type
Celestia.
Our second assignment statement
observer = c:getobserver()
copies the return value of
getobserver
into the variable named
observer.
Again, this return value is merely a reference to an object of type
Observer.
The object itself is not copied:
there is only one observer object in this program.
A group of Celx statements may be packaged as a
functionfunction,
shown below.
The statements are called the
body
of the function,
and are surrounded by the keywords
function
and
end.
To make the keywords more conspicuous,
the body of the function indented.
Our convention is to name the first function
mainmain (function),
but this is not required by the language.
In fact, the function is not actually named
main,
just as the
celestia
object is not actually named
celestia.
main
is merely a variable that refers to the function,
just as
celestia
is a variable that refers to the object.
See the comment alongside the word
main.
Packaging the program as a set of functions will let us control
how long our variables and objects stay alive.
Recall that our original program left behind the variables
observer
and
position
and the objects to which they refer.
This is wasteful—and a potential breach of security
because a subsequent program could manipulate those objects.
To ensure that each variable, object, and function
is destroyed as soon as possible,
we will mark every variable with the keyword
locallocal variable.
A local variable created inside the body of a function
will exist only as long as the function is being executed;
an example is the following variable
observer.
A local variable created outside the body of a function
will exist only as long as the program is being executed;
an example is the following variable
main.
As soon as an object or function has no more variables referring to it,
the object or function is no longer accessible to any program
and can be automatically incinerated by the
Lua
garbage
collector.
--[[
Create and call a function named main.
]]
local function main() --this line can also be written local main = function()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:getobserver()
local position = celestia:newposition(0, 0, 1)
observer:setposition(position)
celestia:print("Hello, world!", 10)
wait()
--[[
The variables observer and position will be destroyed when we reach the
following word "end". Since there are no other variables that refer to
the Observer and Position objects, these objects may now be destroyed at
any time by the Lua garbage collector.
]]
end
--[[
The following statement calls (i.e., executes) the main function.
This will execute the five statements that constitute the body of the function.
]]
main()
--[[
The variable main will be destroyed when we reach the end of the program. Since
there are no other variables referring to the function, the function may now be
destroyed by the garbage collector. As usual, Celestia keeps running after the
Celx program is over.
]]
We prefer to create each variable inside of a function. But there are two occasions when we cannot do this. First, each time a local statement is executed, it creates a new variable. If the statement is in a function that is called many times, it will therefore create many variables. If we want a single variable, the variable will have to be created outside of every function. The most common example will be a variable used by each call to a tick handler function (tickHandler).
Second,
a variable created in a function can be mentioned only within that function.
If the variable needs to be mentioned outside of a function,
or in more than one function,
the variable will have to be created outside of every function.
The most common example will be the variable
main,
which we will always mention on the last line of a program,
outside of every function.
Celx requires two special groups of functions to be nonlocal: the callback functions in callback and the scripted orbits and rotations in scriptedOrbit. All of our other functions will be local.
Celx
functionsfunction
fall into two groups,
the methods and the non-methods.
A
methodmethod
belongs to an object and can read and write the data in the object.
For example,
the following call to
setposition
sets the position of the
observer
object to which the method belongs.
The object and its method are joined with a colon.
observer:setposition(position)
A note on nomenclature.
To call this method in a Celx program,
we write the name of a
variable
in front of the colon.
But to talk about the method itself,
quite apart from any particular object of class
Observer,
we write the name of a
class
in front of the colon.
The name of a Celx class starts with an uppercase letter.
Thus we have just called the
Observer:setposition
method of the object to which the variable
observer
refers.
A
non-method
function is called with a dot
and cannot read or write the object in front of it.
For example,
the following functions
random
and
sqrt
get no data from the object
math.
This object is just a convenient last name or family name
for grouping these functions together.
We will see in
arrayOfStrings
and
standard
that
math
and
std
are actually “tables”.
local x = math.random()
local y = math.sqrt(x)
local c = std.utf8(0x0041) --the string "A"
os.exit(0) --Terminate the Celx program and then terminate Celestia.
Some non-method functions are orphans, belonging to no object at all. They are written without any dot or colon. local s = tostring(10) local t = type(s) print("to the standard output") wait() --a non-method function that Celestia added to Lua main() --a non-method function that we created ourselves For the three non-method functions that Celx added to Lua, see additions.
We often call a method of an object returned by a previous method call. For example, local observer = celestia:getobserver() observer:setposition(position) These two statements could be telescoped into one statement. celestia:getobserver():setposition(position)
A longer sequence such as
local earth = celestia:find("Sol/Earth")
local position = earth:getposition()
local x = position:getx() --position contains x, y, z coordinates.
can be telescoped to
local x = celestia:find("Sol/Earth"):getposition():getx()
By the way,
this
x
is our first variable
that does not contain a reference to an object or to a function.
It contains a plain old number.
Telescope the following chain into a single statement
that creates the same variable
length.
Do not bother to create the variables
observer,
orientation,
or
axis.
local observer = celestia:getobserver() --observer is an Observer.
local orientation = observer:getorientation() --Which way is he facing?
local axis = orientation:imag() --axis is a Vector.
local length = axis:length() --length is a number.
Many methods return an object.
Some methods return a function.
See the eye-popping method
Object:phases
in
phases.
By default, a program executes its statements one at a time from top to bottom. The control structure of a program causes it to execute its statements in a different order. Celx inherits its plain vanilla control structure statements from the language Lua. For examples, see the following sections and their exercises.
| functions | function/end |
create a user-defined function |
| callback | return |
return a value from a user-defined function |
| tickHandler | return |
return without a value from a user-defined function |
|
||
| osExit | if/then/end |
|
| callback | if/then/else/end |
|
| callback | if/then/elseif/end |
|
|
||
| callback | while/do/end |
test at top of loop |
| wait | for/do/end |
test at top of loop (numeric for loop) |
| arrayOfStrings | for/do/end |
test at top of loop (generic for loop, with an iterator) |
| stefanBoltzamnn | repeat/until |
test at bottom of loop |
| inputFile | break |
break out of loop |
| Recursion | recursion |
For a loop that counts by twos,
see the oblate spheroid example in
kilometer.
For a loop that counts backwards,
see the definition of the method
Object:family
in the file
std.lua
in
stdCelx.
For an
infinite loop, see the
while
true do
in
parallax.
Celx has no
switch
or
continue
statements.
To terminate the Celx program without terminating Celestia, call
the Lua functions
error
or
assert
(assert).
To terminate the Celx program and terminate Celestia, call
os.exitos.exit
(osExit).
wait
Function
The Celx function
wait
gives Celestia a chance to update the picture in the window.
Until we call
wait,
the picture will not change
and the text will not be printed.
Even the simulation time
will remain frozen
(settime).
During the call to
wait,
the picture can move and
the simulation time can advance.
In fact,
it is only during a
wait
that these things can happen.
Another thing that can happen only during a
wait
is a call to the
input function
celestia_keyboard_callback
(callback);
see the
while
loop in
callback.
As soon as a Celx program is over,
Celestia automatically regains control and does any overdue rendering.
Thus the
wait
we saw in
programItself
and
functions
was unnecessary
since those programs took only a fraction of a second to run.
But we will write the
wait
anyway,
because it might become necessary if the code were modified.
In a long program,
for example,
wait
must be called at least once every five seconds of real time.
A program that tries to run too long without calling
wait
will be terminated with the message
Error: Timeout: script hasn't returned control to celestia
(forgot to call wait()?)
(Even if the program ends in this ignominious manner,
the function
celestia_cleanup_callback
will still be called
[callback]).
The five-second limit could easily be reached by a program looping through
Celestia’s database of a hundred thousand stars.
For this reason,
the limit can be temporarily extended by
Celestia:settimeslice.
wait
takes an optional argument giving the number of real-time seconds it will take
to return.
This can be used to give a long-running special effect such as
Observer:goto
time to complete its execution,
or to give the user time to read a message.
Warning.
The Celx function
wait
is implemented as a call to the Lua function
coroutinecoroutine.yield.
A call to
wait
will therefore never return
if it is inside a callback function
(callback),
an event handler
(eventHandler),
a Lua hook
(luaHookFunctions),
the
position
method of a scripted orbit
(scriptedOrbit),
the
orientation
method of scripted rotation
(scriptedRotation),
or a Lua
“coroutine”.
Insert the following empty
for
loop into
hello.celx
in
functions
immediately before the
wait.
The
10^
means
109 = 1,000,000,000.
^ (exponentiation operator)9
Does the program crash after 5 seconds?
Now insert the following statement immediately before the
for
loop.
Does the program still crash?
os.exitCelestia normally continues to run after a Celx program has finished. But the program can also terminate Celestia; see standardOutput for an example involving “standard output”.
The Lua function
os.exit
terminates the Celx program and then terminates Celestia.
The function
celestia_cleanup_callback
in
callback
will not be called.
The argument of
os.exit
is the
exit status
number that Celestia will return to the operating system.
In most operating systems,
zero means success and any nonzero number means failure.
To
get permissionaccess policy
to mention the variable
osos
(and the variable
ioio
in
standardOutput
and
outputFile)
we must edit the configuration file
celestia.cfgcelestia.cfg (configuration file)
and change the parameter
ScriptSystemAccessPolicyScriptSystemAccessPolicy (parameter in celestia.cfg)
to
"allow"
or
"ask",
and relaunch Celestia.
The program must also call the method
Celestia:requestsystemaccess,
even if the access policy is
"allow".
And if the access policy is
"ask",
the program must also call
wait.
No argument is necessary for the
wait.
--[[
Demonstrate os.exit, if possible.
]]
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:getobserver()
local position = celestia:newposition(0, 0, 1)
observer:setposition(position)
--Get permission to mention os. Will ask a question if
--ScriptSystemAccessPolicy is "ask" in celestia.cfg.
celestia:requestsystemaccess()
wait()
local duration = 5
if os ~=~= (not equals operator) nil then --The operator ~= means "is not equal to".
--Arrive here if the access policy was "allow",
--or if the access policy was "ask" and the answer was "yes".
celestia:print("The Celx program will cause Celestia to exit.",
duration)
wait(duration)
os.exit(0) --0 for success
end
--Arrive here if the access policy was "deny",
--or if the access policy was "ask" and the answer was "no".
celestia:print("The Celx program can't cause Celestia to exit.",
duration)
wait(duration)
end
main()
If the access policy is
"ask",
Celestia:requestsystemaccess
will ask the following question.
WARNING:
This script requests permission to read/write files
and execute external programs. Allowing this can be dangerous.
Do you trust the script and want to allow this?
y = yes, ESC = cancel script, any other key = no
Say yes.
If you don’t,
the Celx program will end but Celestia will keep running.
To see the exit status returned by Celestia to a Unix operating system,
open a shell window.
For example, on a Mac, open the Terminal window.
In this window,
launch Celestia and the Celx program with the following command.
Follow it with an
echo
to display the exit status.
Celestia hello.celx
echo $? (most Unix shells, including Mac Terminal and Linux)
echo $status (Unix C shell)
To see the exit status in
on Microsoft Windows,
launch
cmd.exe
to open the Command Prompt window.
In this window,
launch the Celx program with the following command
start /wait
command.
Follow it with an
echo
to display the exit status.
help start
start /wait hello.celx
echo %errorlevel%
If the program has a nonlocal function with the special name
celestia_keyboard_callbackcelestia_keyboard_callback (function),
it will be called automatically whenever a character key is pressed.
“Characters”
include letters, digits, punctuation marks,
the blank and tab,
delete (backspace), and return.
Characters do not include the control, option, and command combinations,
the Home and End keys,
the four arrow keys,
and Escape.
For these special keys, write the
keydown
Lua hook in
luaHookFunctions.
The characters must be typed into the Celestia window,
not the command window from which Celestia was launched.
celestia_keyboard_callback
must be enabled by the method
Celestia:requestkeyboard.
Once enabled,
celestia_keyboard_callback
will be called even if the program is in the middle of a
wait
(wait).
In fact,
that’s the only time it can be called.
See the following
while
loop.
The argument received by
celestia_keyboard_callback
is the key that was pressed.
The following assertions
(assert)
are primarily for documentation:
I don’t expect them to fail.
The callback returns
true
to indicate that the character has been completely handled by the callback
and that no further processing is necessary.
This means that the character will not be executed
as a Celestia keyboard command
(play).
For example,
d
will not run the demo
and
;
(semicolon)
will not toggle the equatorial grid.
Returning
false
will allow the character to be executed as a keyboard command.
A missing return statement is equivalent to returning
true.
The following program accepts one line of keyboard input
spelling out a decimal number,
possibly including a negative sign, decimal point, and exponent.
For example,
the line
-123.456e-2
represents the number
–123.456 × 10–2
=
–1.23456.
The
main
function and the callback function communicate via the variable
n.
They display the input line,
the cursor character,
and the error message (if any)
as the input line is being accumulated.
celestia_keyboard_callback
should concentrate on accumulating the characters of input
and recognizing special characters such as backspace and return.
The time-consuming astronomical calculations should be triggered by a flag
and performed
outside
the callback function.
There should be no need for the callback function to call
wait.
In fact, a
wait
in a callback function will never return.
The operator
==== (equals operator)
performs comparison for equality
(no space between the equal signs).
The operator
.... (concatenation operator)
performs string
concatenation
(no space between the dots).
The characters
\r\r (carriage return character)
and
\n\n (newline character)
are the
carriage returncarriage return (character)
and
newlinenewline (character).
Multiple lines have to be printed as a single string,
by means of a single call to
Celestia:print,
because each call to
this method erases the previous text.
--[[ Let the user input a number from the keyboard. Store it in n and print it. ]] --variables used by celestia_keyboard_callback: local n = nil --Remains nil until we receive valid number and return key. local line = "" --Accumulate the line of input that the user types. local errorMessage = "" function celestia_keyboard_callback(c) --can't be local assert(type(c) == "string") if c == "\r" then --return key on Mac, Enter key on Microsoft Windows n = tonumber(line) --Try to convert string to number. if n == nil then errorMessage = "\nThat wasn't a number. Try again." end else errorMessage = "" --Give user the benefit of the doubt. if c ~= "\b" then --backspace (Mac delete, Windows Backspace) line = line .. c --Append the char to the line. elseif line:lenstring.len() > 0 then --If the line has a last char, line = line:substring.sub(1, -2) --remove the last char. end end return true --Do nothing else with this character. end local function main() --Keep the Sun in view, but get away from its glare. local observer = celestia:getobserver() local position = celestia:newposition(0, 0, 1) observer:setposition(position) local cursor = "_" celestia:requestkeyboard(true) --Enable celestia_keyboard_callback. while n == nil do celestia:print("Type a number and press Return.\n" .. line .. cursor .. errorMessage) wait() --Let Celestia call celestia_keyboard_callback. end --Arrive here after user has typed a valid number and pressed return. assert(type(n) == "number") celestia:requestkeyboard(false) --Disable celestia_keyboard_callback. local duration = 5 celestia:print("The number was\n" .. n, duration) wait(duration) end main()
A number can hold up to 15 significant digits
(doubleArithmetic),
but only at most 14 of them will print in the default format
(numericFormatting).
To get all 15, see the
string.format
in
stringFormat.
Add a nonlocal function named
celestia_cleanup_callbackcelestia_cleanup_callback (function)
to your program.
Verify that it is called automatically after the program ends,
even if the ending is ignominious:
a call to
error,
an assertion failure
(assert),
or death by not calling
wait
(wait).
Verify that the cleanup callback will not be called
if the user terminates the program with the escape key,
or if the program calls
os.exit.
It will also not be called as long as there is an event handler
(eventHandler).
function celestia_cleanup_callback()
celestia:print("Goodbye.", 5)
--Do not call wait in a callback function.
--If you want to prevent the next Celx program
--from inheriting this callback function,
celestia_cleanup_callback = nil
end
A Celx program can detect four types of
eventsevent,
represented by the strings
"key",
"mousedown",
"mouseup",
and
"tick".
Four functions, called
event handlers,
can be called automatically when the events occur.
The handlers are enabled by the method
Celestia:registereventhandler.
An event handler will go on being called
after the last line in the program has executed.
The handler will be called
even if the user has cancelled the program with the escape key,
or if the program has died by not calling
wait
(wait).
To disable a handler,
see the exercise in
tickHandler.
The error messages from a handler are
displayed in the console
(console).
The simplest event is a
tick
of the Celestia simulation.
The simulation “ticks”
about 60 times per second of real time
when the
main event loop
of the graphics package is idle.
The tick consists of a call to the C++ member function
CelestiaCore::tick
in
version/src/celestia/celestiacore.cpp.
The handler for this event receives one argument,
which is a table containing a field named
dt
giving the number of real-time seconds since the last tick.
dt
will be about 1/60,
except for the first time this function is called.
See
arrayOfStrings
for tables
and
tableOfFields
for fields.
The assertion
(assert)
in the handler is primarily for documentation.
The handler prints the current simulation time in
UTC,
marching in sync with the time display in the upper right corner of the window.
See
time
for UTC vs. TDB.
The number of percent signs in the first argument of
string.format
must be equal to the number of subsequent arguments.
(The first argument is composed of two concatenated strings
and contains a total of seven percent signs.)
The format
format%d
prints a number as a decimal integer.
The format
%02d
prints it as a decimal integer with at least two digits.
If the number has only one digit,
a leading zero will be supplied.
The last four arguments of
Celestia:print
put the string up in the upper right corner of the window;
see
celestiaPrint.
The most common use of a tick handler is to update the display text, or the observer’s position or orientation. A handler may also be used to print OpenGL graphics (opengl) or to trigger an action when a certain time has been reached. For an example in real time, see the exercise below; for simulation time, see settime. The tick handler in radiantPoint measures the speed of a celestial object by recording the object’s position at two consecutive ticks, and dividing by the interval of simulation time between the ticks.
--[[
Call the tickHandler function every time the Celestia clock ticks.
]]
local function tickHandler(t)
--t.dt is the number of real-time seconds since the previous tick.
assert(type(t) == "table" and type(t.dt) == "number")
--Get the current simulation time (not the current real time).
local utc = celestia:tdbtoutc(celestia:gettime())
local s = string.format(
"%d/%d/%d %02d:%02d:%02d UTC\n"
.. "seconds since last tick: %.15g",
utc.month, utc.day, utc.year,
utc.hour, utc.minute, math.floor(utc.seconds),
t.dt)
--Don't risk division by zero.
if t.dt ~= 0 then
--Append another line to s.
s = s .. string.format("\nTicks per second: %.15g", 1 / t.dt)
end
celestia:print(s, 1, 1, 1, -28, -3)
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:getobserver()
local position = celestia:newposition(0, 0, 1)
observer:setposition(position)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
12/31/2013 08:12:08 UTC
Seconds since last tick: 0.016762971878052
Ticks per second: 59.655293063477
Stop calling the
tickHandler
after the program has been running for 10 seconds.
Insert the following
code after the
assert.
Pulse the constellation stick figures in red every two seconds.
seconds
is the number of real-time seconds since the start of the program.
cycles
is the number of two-second cycles.
x
starts at 0 and increases by
2π
during each cycle.
The sine starts at 0 and goes up, down, and back to 0 during each cycle,
contributing to the amount of red in the color.
A handler can also be registered for the
"key"
event.
It is similar to the
celestia_keyboard_callback
in
callback,
but can be called when the program is not executing a
wait.
It can even be called even after the Celx program has terminated.
Unlike
celestia_keyboard_callback,
the handler will be called for both control and non-control keys.
A control key will be received as a three-character string.
For example, the Macintosh delete key is received as
"C-h"
because the ASCII code of a backspace is 8,
and h is the eighth letter of the alphabet.
Similarly, a return is received as
"C-m"
because the ASCII code of a carriage return is (decimal) 13.
The four arrow keys are not received by this handler;
see
luaHookFunctions
to catch them.
The keystrokes must be typed into the Celestia window,
not the command window from which Celestia was launched.
As in
celestia_keyboard_callback,
a return value of
true
prevents the character received by the handler
from being executed as a Celestia keystroke command.
A missing
return
statement in a key handler
is equivalent to returning
false.
Let’s write a handler to intercept a typical Celestia keystroke command. The argument of the handler, and the renderflags, are tables of fields. For fields in general, see tableOfFields. For the renderflags table in particular, see renderFlags.
--[[
Intercept the user's semicolon keystrokes which toggle the equatorial grid.
]]
local function keyHandler(t)
assert(type(t) == "table" and type(t.char) == "string")
if t.char == ";" then
local flags = celestia:getrenderflags()
if flags.grid then
--Grid is on,
--and will be turned off after the keyHandler returns.
celestia:print("Equatorial grid off.")
else
--Grid is off,
--and will be turned on after the keyHandler returns.
celestia:print("Equatorial grid on.")
end
end
return false --Let the keystroke be executed as a command.
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:getobserver()
local position = celestia:newposition(0, 0, 1)
observer:setposition(position)
celestia:registereventhandler("key", keyHandler)
celestia:print("Press semicolon to toggle the equatorial grid.", 10)
wait()
end
main()
Handlers can be registered for the
"mousedown"
and
"mouseup"
events.
For
"mousemove",
see
luaHookFunctions.
The
x, y
coördinates are nonnegative integers measured in pixels
from an origin in the upper left corner of the Celestia window.
Returning
true
from the handler will prevent Celestia from selecting
the object that was clicked on.
A missing
return
statement in a mouse handler
is equivalent to returning
false.
local function mousedownHandler(t)
assert(type(t) == "table" and type(t.button) == "number"
and type(t.x) == "number" and type(t.y) == "number")
celestia:print("mouse button number = " .. t.button
.. " at pixel (" .. t.x .. ", " .. t.y .. ")", 5)
return false --Let the click select an object.
end
Functions can be called automatically on nine more occasions,
represented by the following strings.
"charentered"
These functions, called
Lua hooks,
must be written in a separate file.
Our convention is to name the file
"keydown"
"mousebuttondown"
"mousebuttonmove"
"mousebuttonup"
"mousemove"
"renderoverlay"
"resize"
"tick"luahook.celx
and place it in the Celx directory
(celxDirectory).
The filename is specified by placing the following parameter
within the
{curly braces}
of the
Configuration
section of
celestia.cfgcelestia.cfg (configuration file).
(The parameter will have to be rewritten with a slash
if a Lua hook calls the methods
Celestia:loadtexture
or
Celestia:runscript.)
#excerpt from celestia.cfg
LuaHook "luahook.celx"
luahook.celx
is executed once, when Celestia is launched.
It creates a table containing the hooks and passes it to the method
Celestia:setluahook.
The hooks will be called automatically at the appropriate times.
When a hook is called,
the table is passed to the hook as the
self
argument of the hook.
Using this argument,
the hook can access all of the table’s fields.
The table acts like an
objectobject (in programming language)
in an object-oriented language:
the hooks are the object’s methods
and the other fields of the table are the object’s instance variables.
See
Geostationary
for a similar “object” implementing a scripted orbit.
On all platforms, the
charenteredcharentered (Lua hook)
hook receives all normal characters.
On Macintosh, it also receives command characters but not control characters.
On Windows, it receives control characters.
A Mac command character or a Windows control character is received by
charentered
as a three-character string such as the
"C-h"
we saw with the
"key"
event handler in
keyHandler.
The keystrokes must be typed into the Celestia window,
not the command window from which Celestia was launched.
The
keydownkeydown (Lua hook)
hook is called for special keys:
the four arrows,
Home and End,
the numeric keypad,
some of the function keys,
and the letters a and z.
See
orbitObserver
for an example with the arrow keys.
The arguments of
mousebuttondownmousebuttondown (Lua hook),
mousebuttonupmousebuttonup (Lua hook),
and
mousemovemousemove (Lua hook)
are the x, y coördinates
of the mouse.
They are nonnegative integers measured
from an origin at the upper left corner of the window.
On most platforms,
the arguments of
mousebuttonmove
are the change in the coördinates
since the last call to
mousebuttonmove.
These numbers will be negative for a move to the upper left,
but will always be close to zero.
We will use these numbers in
opengl
to drag a graphic across the window.
mousebuttonmove
makes little sense in Microsoft Windows.
It is called for every mouse move, even when the mouse button is not pressed.
Before the first press,
its arguments give the offset from the origin in the upper left corner.
After the mouse button is pressed and released at the same position,
the arguments give the offset (positive or negative) from that position.
While the mouse is being dragged,
the arguments are zero and zero.
After a drag,
the arguments are the offset of the mouse
from the center of the Celestia Window.
The
renderoverlayrenderoverlay (Lua hook)
hook is called each time the transparent overlay on the Celestia window
is rendered.
This happens many times per second,
approximately with each tick of the simulation.
The overlay contains text such as
the name of the selected object in the upper left corner,
the current time in the upper right,
and the output of
Celestia:print.
All OpenGL graphics must be drawn in
renderoverlay
or in a tick handler
(tickHandler).
See the examples in
opengl
Analemma,
Sundial,
and
project.
The
resizeresize (Lua hook)
hook is called when the Celestia window is resized,
including the initial sizing when the window is created.
The width and height are nonnegative integers measured in pixels.
Most hooks return the value
false
by default.
This causes the keystroke or mousemove that triggered the hook
to have its normal effect after the hook has finished.
For example,
a keystroke will be executed as one of the keystroke
commands in
keystroke.
A return value of
true
allows nothing else to happen.
It indicates that the keystroke or mouse move
has been completely serviced by the hook,
and that no further action is necessary.
--[[
This file is luahook.celx.
Create a table named luaHook containing 18 fields.
The values of the first 9 fields are strings.
The values of the last 9 fields are methods.
]]
local luaHook = {
charenteredString = "",
keydownString = "",
mousebuttondownString = "",
mousebuttonmoveString = "",
mousebuttonupString = "",
mousemoveString = "",
renderoverlayString = "",
resizeString = "",
tickString = "",
charentered = function(self, char)
assert(type(self) == "table" and type(char) == "string")
self.charenteredString = "charentered(\"" .. char .. "\")"
--The default; let a character or a control character
--be executed as a keystroke command.
return false
end,
keydown = function(self, key, modifiers)
assert(type(key) == "number" and type(modifiers) == "number")
self.keydownString = "keydown(" .. key .. ", " .. modifiers
.. ")"
if key ~= 0 then
self.keydownString = self.keydownString
.. " \"" .. string.char(key) .. "\""
end
--The default; let a function key or numeric keypad digit (try
--"4" and "6") be executed as a keystroke command.
return false
end,
mousebuttondown = function(self, x, y, button)
assert(type(button) == "number")
self.mousebuttondownString = "mousebuttondown(" .. x .. ", "
.. y .. ", " .. button .. ")"
return false --the default; let user drag border of splitview
end,
mousebuttonmove = function(self, dx, dy, modifiers)
assert(type(modifiers) == "number")
self.mousebuttonmoveString = "mousebuttonmove(" .. dx .. ", "
.. dy .. ", " .. modifiers .. ")"
return false --the default; let user drag on sky
end,
mousebuttonup = function(self, x, y, button)
assert(type(button) == "number")
self.mousebuttonupString = "mousebuttonup(" .. x .. ", " .. y
.. ", " .. button .. ")"
return false --the default; let user select the object
end,
mousemove = function(self, x, y)
self.mousemoveString = "mousemove(" .. x .. ", " .. y .. ")"
return false --the default; let user drag on sky
end,
renderoverlay = function(self)
self.renderoverlayString = "renderoverlay()"
--When printing in upper left corner of window, 6th argument
--must be <= -1 to avoid chopping off top line of text.
celestia:print(
self.charenteredString .. "\n"
.. self.keydownString .. "\n"
.. self.mousebuttondownString .. "\n"
.. self.mousebuttonmoveString .. "\n"
.. self.mousebuttonupString .. "\n"
.. self.mousemoveString .. "\n"
.. self.renderoverlayString .. "\n"
.. self.resizeString .. "\n"
.. self.tickString,
1, -1, 1, 1, -1)
--Return value is ignored.
end,
resize = function(self, width, height)
self.resizeString = "resize(" .. width .. ", " .. height .. ")"
--Return value is ignored.
end,
tick = function(self, dt) --dt is seconds since last tick
self.tickString = "tick(" .. dt .. ")"
if dt ~= 0 then
self.tickString = self.tickString
.. " ticks per second = " .. 1 / dt
end
--Return value is ignored.
end
}
celestia:setluahook(luaHook)
--Don't call the wait function in this file.
Launch Celestia, either with or without a Celx program. Press the keys, move the mouse, and resize the window.
charentered(";") keydown(59, 0) ";" mousebuttondown(576, 216, 1) mousebuttonmove(0, -1, 1) mousebuttonup(576, 216, 1) mousemove(576, 216) renderoverlay() resize(683, 465) tick(0.016816139221191) ticks per second = 59.466681789826
Warning 1.
Always check the Celestia console
(console)
when using Lua hooks,
because that’s the destination for error messages produced by the
assert
and
error
(assert)
functions in
luahook.celx.
Be careful of uppercase vs. lowercase mistakes.
As usual,
nonexistent variables and functions are given the value
nil,
which will probably trigger additional errors—sixty times per second.
Warning 2.
There is no direct way for the regular Celx program
(e.g., hello.celx)
to communicate or synchronize its actions
with the hooks in
luahook.celx.
A trick you could try is the
Celestia:settimescale
workaround in
traceRetrograde.
It may be possible to make part or all of the problem disappear
by writing code in a tick handler
(tickHandler)
rather than in the "tick" Lua hook.
Warning 3.
Celestia creates the table of Lua hooks
very early in the startup process,
before the solar system catalog
(.ssc)
files are read.
Therefore
Celestia:find
cannot be called when the hooks are being created.
find
can be called later,
however,
when the hooks are called.
A similar technique must be employed to “require”
the Celx standard library in
luahook.celx.
See
standard.
How many times per second is the
renderoverlay
hook called?
Call the method
Celestia:getscripttime
which,
in
luahook.celx,
returns the number of seconds since
luahook.celx
was first read.
Verify that the
celestia
object in
luahook.celx
is a different object than the
celestia
object in the main Celx program.
Thus there are actually two object of class
Celestia,
contradicting what we said in
objectsAndClasses.
Unfortunately,
this eliminates one possible means of communication
between the regular Celx program and the Lua hooks.
tostring (Lua function) function that renders a celestia
object as the uninformative string "[Celestia]".
With that function out of the way, we automatically uncover a better
"tostring" function that displays the ID number of the celestia object.
]]
local metatablemetatable (Lua) = getmetatablegetmetatable (Lua function)(celestia)
local save = metatable.__tostring --two underscores
metatable.__tostring = nil
--Call the better "tostring" function.
local s = "This celestia object is " .. tostring(celestia)
--Restore the boring "tostring" function.
metatable.__tostring = save
This celestia object is userdata: 0x8e453b4
Verify that
luahook.celx
and the main Celx program are executed by two different Lua
threadsthread.
In Lua 5.1,
the function
coroutinecoroutine.running
returns only one value.
When a key is pressed, up to four Celx functions can be called automatically. In addition, the key can also be executed as a Celestia keystroke command. These functions are called in the following order.
celestia_keyboard_callback in
callback"key" event handler in
keyHandlercharentered
Lua hook in
luaHookFunctionskeydown
Lua hook in
luaHookFunctions
Each of the first four functions can return
true
to prevent the subsequent steps from happening.
This value means that the keystroke that triggered the function call
has been completely serviced by the function,
and no further action is necessary.
One exception:
the
keydown
hook, if present,
is always called.
LuaState::init
in
version/src/celestia/celx.cpp
This book presents a
Standard Library
of classes, functions, and objects
to provide the values and services most commonly needed in Celx programming.
For example,
the standard position at the start of many programs,
celestia:newposition(0, 0, 1),
has been created once and for all in the library as the object
std.position.
The prefix
“std.”
means that the position belongs to a table named
std.
See
tableOfFields
for tables.
The features offered by the library fall into three groups.
std.position
and the vector
std.xaxis,
convenient arrays such as
std.monthName
and
std.zodiac,
and physical constants such as
std.pixelsPerIn
and
std.tilt
(the tilt of the Earth’s axis in radians,
approximately 23°).
Position
(position)
and
Vector
(vectors),
that contain the same Cartesian coördinates
but have to be handled differently.
For example, the method
Frame:from
accepts a
Position
but not a
Vector,
while
Rotation:transform
accepts a
Vector
but not a
Position.
The library makes
Position
and
Vector
more interchangeable.
RotatedFrame.
The source code of the library is the file in
stdCelx.
To install it,
store it in a plain text file named
std.luastd.lua (file)
in the Celx directory
(celxDirectory).
After creating or modifying this file,
Celestia must be relaunched.
To access the library,
the following program calls the Lua function
requirerequire (Lua function).
The
parentheses( ) (omitted for string argument)
are not needed when the function argument
is a
double-quotedquotes around string
string,
so we could have omitted them.
But the Celx programmer probably has to switch back and forth
on an hourly basis
to languages where the parentheses are required,
so we leave them in.
To verify that the library has been loaded,
we check that there is a field for it in the
package.loadedpackage.loaded
table.
The method
saneCelestia:sane
is added to class
Celestia
when we
require
the standard library.
It was inspired by the Unix command
stty sane
and resets the Celestia options to sane values.
It displays the planets but not their orbits,
the moons but not the asteroids,
and the equatorial grid but not the ecliptic grid.
For convenience,
it returns the observer object.
--[[
Demonstrate that a .celx program can use the Celx Standard Library std
in the file std.lua.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
if package.loaded.std == nil then
--require was unable to load the standard library.
--We can't mention anything that starts with std.
local observer = celestia:getobserver()
observer:setposition(celestia:newposition(0, 0, 1))
else
--The standard library loaded successfully.
--It's safe to use all the things that start with std.
local observer = celestia:sane()
observer:setposition(std.position)
local s = "Celx Standard Library version " .. std.libraryVersion
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner
end
wait()
end
main()
Celx Standard Library version 1.1
A C programmer has a rage to cram everything into a single expression.
Since the
observer
is mentioned only once,
we can telescope the first two statements in the
else
to the following.
Does this make the program harder to understand? If so, the C programmer would smile.
As the standard library is created, it calls
Celestia:getobserver.
But the
luahook.celx
file
(luaHookFunctions)
is executed before any observers are created.
This means that
luahook.celx
must not
require("std")
when Celestia starts up.
The library can, however, be
required
later, when the hooks are called.
To ensure that it is
required
only once,
use the following
if.
More examples are in
Analemma,
Sundial,
project,
and
scriptedOrbit.
--[[
This file is luahook.celx.
Can't require("std") up here at the top of the file.
]]
local luaHook = {
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
--But we can require("std") down here.
require("std")
end
--Demonstrate that renderoverlay can use std.
celestia:print("std.libraryVersion = " .. std.libraryVersion, 1)
end
}
celestia:setluahook(luaHook)
std.libraryVersion = 1.1
Normally we would have named the library file
std.celx
since it contains Celx code.
But the
require
function looks for a file whose extension is
.lua.
The
require
gets this extension from the Lua string
package.path,
which by default contains the following pattern.
./?.lua
The first
dot. (current directory)
stands for the current directory (the Celx directory).
The
slashslash (in filename)
(or
backslashbackslash (in filename)
on Microsoft Windows)
separates the directory name from the filename.
The
question mark? (wildcard in package.path)
is a
wildcardwildcard (in package.path)
that will match the string
"std"
passed to
require.
The second dot is part of the
.lua
filename extension.
If we wanted to name the standard library file
std.celx,
we could override the default the contents of
package.path
by creating an operating system
“environment variable”environment variable
named
LUA_PATHLUA_PATH (environment variable)
(uppercase with underscore)
containing the string
./?.celx
(On Microsoft Windows, it would have a backslash.)
But we’re not creating the environment variable,
and I want to explain why.
It is true that the environment variable
would override the default contents of the
package.path
used by the
require
in a regular Celx program.
But the environment variable would not override the default contents of the
package.path
used by a
require
in a
luahook.celx
file
(luaHookFunctions)
or in a scripted orbit or rotation file
(scriptedOrbit).
So we’re going to let the name of the library file remain
std.lua.
--[[
Display the environment variable LUA_PATH and the Lua string package.path.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:requestsystemaccess() --Get permission to mention os.
wait()
local s = nil
local LUA_PATH = os.getenv("LUA_PATH")
if LUA_PATH == nil then
s = "LUA_PATH does not exist."
else
--Put double quotes around it,
--and a backslash in front of each double quote inside it.
s = string.format("LUA_PATH = %q", LUA_PATH)
end
--Change each semicolon to a newline
--to display each pattern in package.path on a separate line.
s = s .. "\n\n" .. package.path:gsubstring.gsub(";", "\n")
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner of window
wait()
end
main()
The following are the outputs on Macintosh and Microsoft Windows.
LUA_PATH does not exist. ./?.lua /usr/local/share/lua/5.1/?.lua /usr/local/share/lua/5.1/?/init.lua /usr/local/lib/lua/5.1/?.lua /usr/local/lib/lua/5.1/?/init.lua LUA_PATH does not exist. .\?.lua C:\Users\Myname\AppData\Local\Celestia\lua\?.lua C:\Users\Myname\AppData\Local\Celestia\lua\?\init.lua C:\Users\Myname\AppData\Local\Celestia\?.lua C:\Users\Myname\AppData\Local\Celestia\?\init.luaWe covered keyboard input and mouse input in callback, eventHandler, and luaHookFunctions because we classified them as language idiosyncrasies. This section covers the more conventional types of i/o.
Celestia:print
on the Celestia Window
The method
Celestia:print
prints on the transparent overlay on the Celestia window.
The color defaults to white and can be overridden by
Celestia:settextcolor.
The same color should be returned by
Celestia:gettextcolor,
but it rounds each rgb component to the nearest 255th.
For example,
the
.5
in the following program
is rounded to
127/255 ≈ 0.498039.
The alpha level is hardwired to 1 (totally opaque).
The
font
and size are specified by the
TitleFontTitleFont
(parameter in celestia.cfg)
parameter in
celestia.cfg:
#Excerpt from celestia.cfg.
#The file sansbold20.txf is in the fonts subdirectory of the Celx directory.
#Don't forget the .txf extension ("texture font") and the double quotes.
TitleFont "sansbold20.txf"
The
TitleFont
defaults to the font specified by the another parameter,
FontFont
(parameter in celestia.cfg),
which defaults to the font
default.txfdefault.txf (font)
in the
fonts
subdirectory of the Celx directory
(celxDirectory).
The font cannot be changed while the Celx program is running.
To see all the
glyphs
in the font,
see
inputFile.
For other uses of fonts,
see the Celestia console in
console,
the OpenGL graphics in
opengl,
and the labels set by
Object:mark.
The following program prints the basic statistics about the color,
font, and size of
Celestia:print.
The
%8g
format prints at least eight characters.
For example, the number 1 will have seven blanks in front of it.
--[[
Print the color and the dimensions of an "em" in the font used by
Celestia:print.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:settextcolor(.5, 1, 1) --red, green, blue; alpha is 1
local red, green, blue = celestia:gettextcolor()
local name = celestia:getparamstring("TitleFont") --case sensitive
assert(type(name) == "string")
if name == "" then --not found
name = celestia:getparamstring("Font")
end
if name == "" then
name = "default.txf"
end
local font = celestia:loadfont("fonts/" .. name)
--another way to get the same font:
--local font = celestia:gettitlefont()
assert(type(font) == "userdata" and tostring(font) == "[Font]")
local mWidth = font:getwidth("M") --Argument can be > 1 character.
local mHeight = font:getheight()
assert(mHeight > 0 and mWidth > 0) --Prevent division by zero.
local windowWidth, windowHeight = celestia:getscreendimension()
local s = string.format(
"red = %8g = %3d/255\n"
.. "green = %8g = %3d/255\n"
.. "blue = %8g = %3d/255\n"
.. "%s: one em is %d x %d pixels.\n"
.. "Window is %d x %d pixels.\n"
.. "Window therefore has room for %d lines of %d ems.",
red, 255 * red,
green, 255 * green,
blue, 255 * blue,
name, mWidth, mHeight,
windowWidth, windowHeight,
math.floor(windowHeight / mHeight),
math.floor(windowWidth / mWidth))
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner of window
wait()
end
main()
red = 0.498039 = 127/255
green = 1 = 255/255
blue = 1 = 255/255
sansbold20.txf: one em is 16 x 24 pixels.
Window is 640 x 480 pixels.
Window therefore has room for 20 lines of 40 ems.
The first argument of
Celestia:print
is the string to be printed,
at most
210 − 1
= 1023
characters.
A longer string will not be printed.
There is no need for the string to end with the newline character
"\n".
For special characters,
see
specialCharacters.
The second argument is the number of real-time seconds
during which the text remains in the window.
It defaults to 1.5,
including a half-second fadeout whose duration
is hardwired into the member function
CelestiaCore::renderOverlay
in
version/src/celestia/celestiacore.cpp.
To prevent the program from advancing to the next statement
while the text is visible,
follow the
print
with a
wait
of the same duration.
local duration = 5
celestia:print("Your message here.", duration)
wait(duration) --until the print fades away
--Or you could use std.duration, which is also 5.
To keep the text visible forever,
or until overwritten by another call to
Celestia:print,
use a duration of
math.huge.
The remaining arguments of
Celestia:print
are optional pairs of integers specifying a location in the window.
The first pair represents the origin for the text.
Each integer should be 0 or
±1.
-1, 1 |
upper left | 0, 1 |
top | 1, 1 |
upper right |
-1, 0 |
left | 0, 0 |
center | 1, 0 |
right |
-1, -1 |
lower left | 0, -1 |
bottom | 1, -1 |
lower right |
The next pair of integers
is the horizontal and vertical offsets from the text origin,
measured in
ems.
Fractions will be ignored.
The two pairs default to
-1, -1, 0, 5,
representing a point
five lines above the lower left corner of the window.
Celestia:flash
prints at the same place.
Warning: with an origin at the top of the window, the vertical offset from the origin must be less than or equal to –1 to prevent the top line of text from being cut off. In other words, if the fourth argument is 1, the sixth argument must be less than or equal to –1.
Use the OpenGL functions in
opengl
for control over the alpha level
and for pixel-level control over the location of the text.
OpenGL also permits tilted and superimposed strings,
multiple fonts and colors at the same time,
and strings longer than 1023 characters.
To print on a window divided into multiple views,
see the
splitview
example in
Iapetus.
The center of the window is the direction of the observer’s view.
Let’s mark this point with a pair of characters.
The exact center will be between the characters, at their
baseline.
The first character has to be an uppercase M
because the fifth argument of
Celestia:print
is in ems.
If you can’t see the characters,
drag the Sun away from the center of the window.
To mark the center of the window with crosshairs, see opengl.
Celestia:log
to the Celestia Console
The Celestia debugging
console
displays the
standard
error output
produced by Celestia itself.
The console also displays the text written by a Celx program with the method
Celestia:log.
The method
accepts one string argument,
to which a newline will be automatically appended.
Unlike
Celestia:print,
a call to
Celestia:log
does not overwrite the previous call’s text.
The console has room for only 200 lines of text,
a default overridden by the
LogSizeLogSize (parameter in celestia.cfg)
parameter in
celestia.cfg.
(Actually, one less: 199.)
A line longer than 120 characters will be split,
counting as two separate lines for the 200-line limit.
The color (white) and alpha level (1)
are hardwired into the member function
CelestiaCore::draw
in
version/src/celestia/celestiacore.cpp.
The font is specified by the
FontFont
(parameter in celestia.cfg)
parameter in
celestia.cfg:
#Excerpt from celestia.cfg.
Font "sans12.txf"
It defaults to
default.txf.
Let’s list the image files that are loaded when we go to the Earth:
--[[
Go to the Earth, causing its texture (image) files to be loaded.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:log("About to go to Earth. The console font is "
.. celestia:getparamstring("Font") .. ".")
local earth = celestia:find("Sol/Earth")
observer:goto(earth, std.duration) --std.duration is 5 seconds.
wait(std.duration) --Wait until goto is finished.
celestia:log("We have gone to Earth.")
wait()
end
main()
Press
~ (tilde)
to toggle the console,
the up and arrow arrows to scroll it,
and
Page Up
and
Page Down
to scroll ten lines at a time.
The text written by
Celestia:print
and
Celestia:log
can easily be read by a human being.
But it would be hard for another program to read this text,
since it is written in pixels in a window.
Data intended for consumption by another program,
or for storage in a file,
should be written to Celestia’s
standard
output
and
standard
error outputstandard error output.
Standard output is for successful output;
standard error is for error messages.
Standard output is produced by the Lua function
printprint (Lua function),
not to be confused with the Celx method
Celestia:print.
The Lua
print
concatenates its arguments and follows them with a newline.
To avoid the tabs and newline,
call the
writewrite
(method of file)
method of the object
io.stdoutio.stdout
(outputFile).
Standard output can also be produced by the method
Object:setatmosphere,
and by the keystroke commands @ and !
in Celestia’s
“super-secret edit mode”.
Standard error output is producted by the
write
method of
io.stderrio.stderr.
Upon success,
write
returns
true
in Lua 5.1,
and returns the
io.stdout
or
io.stderr
object in Lua 5.2.
For access to the variables
io
and
os,
see
osExit.
Sometimes a Celx program is run only for the purpose of producing standard
output.
This is often the case when the program is launched from a Unix shellscript,
or when its standard output is directed into an output file or
pipepipe (Unix).
In this situation,
we usually want the program to quit Celestia with the function
os.exitos.exit
(osExit)
when the output is finished.
The standard output written by
print
might not go to the outside world immediately.
It could be held in an area of memory inside Celestia called a
bufferbuffered i/o.
Successive calls to
print
will fill up more and more of the buffer.
When the buffer is full, all of its data is
flushed
to the outside world in one big convoy.
The buffer is also flushed automatically by
os.exit
when the program ends.
The standard error output is unbuffered and requires no flush.
A Celestia that is launched from the command line
and that produces buffered output such as standard output
must be allowed to die a natural death,
either by selecting Quit or Exit from Celestia’s File menu
or by calling
os.exit.
If Celestia is launched from the command line and then assassinated with a
control-ccontrol-c (keystroke),
the last buffer of standard output might be trapped inside the dying Celestia
and might never emerge.
--[[
Demonstrate standard output (for good news)
and standard error output (for bad news).
]]
local function main()
--Get permission to mention io and os.
celestia:requestsystemaccess()
wait()
if io == nil or os == nil then
celestia:print("Cannot demonstrate standard i/o or os.exit.",
10)
wait()
else
--No newline is appended implicitly.
local r = io.stdout:write("This is standard output ")
assert(r) --r is boolean in Lua 5.1
--Newline is appended implicitly.
print("and more standard output on the same line.")
--No newline is appended implicitly.
r = io.stderr:write("This is standard error output.\n")
assert(r)
--Before the Celestia window disappears,
--give the user time to see that it has no text.
wait(5)
os.exit(0) --flushes the output buffer
end
end
main()
This is standard output
and more standard output on the same line.
Most forms of output are directed
to a destination specified (at least implicitly) in the program itself:
Celestia:print
outputs to the window and
Celestia:log
to the console.
But the standard output and standard error output are sent to destinations
specified in the command line that launched the program.
Let’s take the Macintosh Terminal
as an example;
the other command lines follow the same rules.
--with-glutGLUT (OpenGL Utility Toolkit)
also requires a
-f
argument before the program name.)
Celestia progname.celx
This is standard output and more standard output on the same line.
This is standard error output.
>> (i/o redirection) out.txt
This is standard error output.
2
and the
>.
Celestia progname.celx 2>2> (i/o redirection) err.txt
This is standard output and more standard output on the same line.
2>&12>&1 (i/o redirection)
On Microsoft Windows,
the standard output and standard error output of Celestia
vanish into thin air.
This is because Celestia never creates a Microsoft
“console”console (Microsoft Windows)
by calling the
AllocConsole
function.
The workaround is to write the data to an output file
(outputFile).
Verify that
print
prints only 14 of a number’s
significant digits.
See
doubleArithmetic
and
defaultFormat.
To get all 15 of them,
we must format the number with the Lua function
string.format.
See
floatFormat.
For Unix programmers, we present a filterfilter, Unix that copies its standard input to its standard output. As the standard input flows through the program, it is also copied to the Celestia window.
By default, the standard input comes from the keyboard.
In this case, the keystrokes must be typed into the shell window,
not the Celestia window,
and we must press return at the end of each line.
The standard input can also come from a pipe.
To make the pipe work without human intervention,
set the
ScriptAccessPolicy
in
celestia.cfg
to
"allow"
and relaunch Celestia.
Both
waitwaits
around the following call to
readread (method of file)
are necessary to keep the string
s
up to date.
If either one is missing,
the string lags behind the characters as they are typed.
If both are missing, the tick handler is never called.
On Microsoft Windows,
the
read
method always returns
nil.
The standard output is broken too;
see
standardOutput.
--[[
Copy the standard input to the standard output. Along the way, carbon copy it
into the Celestia window, like the Unix utility teetee (Unix utility).
]]
require("std")
--variable used by tickHandler:
local s = ""
local function tickHandler()
celestia:print(s, 1, -1, 1, 1, -1) --upper left, in case s is multi-line
end
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
celestia:requestsystemaccess() --get permission to mention io and os
wait()
celestia:registereventhandler("tick", tickHandler)
while true do
wait()
local c = io.stdinio.stdin:read(1) --one character
wait()
if c == nil then --end of file
break
end
--Write the standard output in uppercase, so we can tell it
--apart from the standard input in the shell window.
io.stdout:write(c:upper())
s = s .. c
end
--Arrive here on end of file.
celestia:registereventhandler("tick", nil)
local duration = 5
celestia:print(s .. "\nEOF", duration, -1, 1, 1, -1)
wait(duration)
os.exit(0)
end
main()
Standard input comes from a source specified on the command line that launched the program:
--with-glut
also requires a
-f
argument before the program name.)
Celestia progname.celx
For output to a file whose name is specified in the program itself,
we have the conventional trio of
openio.open,
writewrite
(method of file),
and
closeclose (method of file).
The first argument of
io.open
is the name of the output file to be created,
by default in the Celx directory.
The second argument is
"w"
for write.
See
osExit
for access to the variables
io
and
os,
and
standardOutput
for a warning about buffered output.
--[[
Create and open an output file, write to it, and close it.
Check for every checkable error.
]]
local function main()
--Get permission to mention io and os.
celestia:requestsystemaccess()
wait()
if io == nil or os == nil then
celestia:print("Cannot demonstrate file output or os.exit.", 10)
wait()
return --Don't execute any more of the main function.
end
--Open the file.
local name = "outfile.txt"
local handle, message, code = io.open(name, "w") --create or overwrite
if handle == nil then
local s = "couldn't open file " .. name .. "\n"
.. message .. ", code " .. code .. "\n"
io.stderr:write(s)
wait()
os.exit(1) --1 indicates failure on my operating system
end
assert(type(handle) == "userdata" and io.type(handle) == "file")
--Write to the file.
local success, message, code =
handle:write("This output goes to a file on the disk.\n")
if success == nil then
local s = "couldn't write to file " .. name .. "\n"
.. message .. ", code " .. code .. "\n"
io.stderr:write(s)
wait()
os.exit(1)
end
--Close the file.
local success, message, code = handle:close()
if success == nil then
local s = "couldn't close file " .. name .. "\n"
.. message .. ", code " .. code .. "\n"
io.stderr:write(s)
wait()
os.exit(1)
end
assert(type(handle) == "userdata" and io.type(handle) == "closed file")
--os.executeos.execute("chmod 444 " .. name) --change mode: only on Unix systems
wait()
os.exit(0) --0 indicates success on my operating system
end
main()
The program creates the file
output.txt,
containing the following.
Let’s read from one of Celestia’s own data files.
We’ll pick a
.txftxf file (Texture Font)
file (an OpenGL txf font)
to demonstrate textual input
(the first four bytes of the file)
and binary input
(the rest of the file).
The binary numbers are read in 16- and 32-bit sizes,
and in
big-endianendian (byte order)
or little-endian byte order.
To assemble the binary numbers,
we
shift
shift the individual bytes into position by multiplying them
by a power of 2.
For example, multiplying a byte by
28 = 256
shifts it 8 bits to the left.
Lua 5.2 will let us shift the bytes with
bit32.lshift.
This program also demonstrates
random access i/o
with
file:seekseek (method of file).
With the argument
"cur",
this method skips the designated number of bytes
starting from the current position in the file.
The first character in the file is the byte of “all ones”.
Lua 5.2 will let us write this character as
"\xFF",
but Lua 5.1 makes us write it as
"\255".
The
std.utf8
function
(specialCharacters)
converts a Unicode code number into the string of
UTF-8
bytes representing that character.
--[[
Display all the glyphs (characters) that belong to the TitleFont in
celestia.cfg, 16 per line, with the four-hex-digit Unicode number of each glyph.
]]
require("std")
--Read an n-byte integer in binary: 2 or 4 bytes
local reverse = nil --true if bytes need to be reversed
local function read(handle, n)
assert(type(handle) == "userdata" and io.type(handle) == "file"
and (n == 2 or n == 4))
local s = handle:read(n)
assert(type(s) == "string" and s:lenstring.len() == n)
if reverse then
s = s:reversestring.reverse()
end
local b = {s:bytestring.byte(1, n)} --b is an array of n numbers.
assert(type(b) == "table" and #b == n)
local i = 0
for j = 1, n do
i = 2^8 * i + b[j]
end
return i
end
local function main()
local observer = celestia:sane()
local position = celestia:newposition(1, 0, 0) --Sun not in window.
observer:setposition(position)
--Get permission to mention io.
celestia:requestsystemaccess()
wait()
if io == nil then
celestia:print("Cannot demonstrate file input.", 10)
wait()
return
end
local name = "fonts/" .. celestia:getparamstring("TitleFont")
local handle, message, code = io.open(name, "r") --r for "read"
if handle == nil then
local s = "couldn't open file " .. name .. "\n"
.. message .. ", code " .. code
celestia:print(s, 60)
return
end
if handle:read(4) ~= "\255txf" then --a byte of "all ones"
celestia:print("couldn't read four-byte header in " .. name, 60)
return
end
--Do we have to reverse the bytes of the integers read from the file?
local b = {handle:read(4):byte(1, 4)} --b is an array of four numbers.
if b[1] == 0x78 and b[2] == 0x56 and b[3] == 0x34 and b[4] == 0x12 then
reverse = true
elseif b[4] == 0x78 and b[3] == 0x56 and b[2] == 0x34 and b[1] == 0x12
then
reverse = false
else
local s = string.format(
"unfamiliar byte order %02X %02X %02X %02X in %s",
b[1], b[2], b[3], b[4], name)
celestia:print(s, 60)
return
end
handle:seek("cur", 3 * 4) --Skip the next 3 four-byte integers.
local maxAscent = read(handle, 4)
local maxDescent = read(handle, 4)
local n = read(handle, 4) --number of glyphs in font
local s = string.format(
"%s reverse: %s\n"
.. "Max ascent: %u Max descent: %u Number of glyphs: %u\n",
name, tostring(reverse),
maxAscent, maxDescent, n)
for i = 1, n do
local unicode = read(handle, 2) --unicode character number
s = s .. string.format("%04X %s ", unicode, std.utf8(unicode))
--Display 16 glyphs of the font per line.
if i % 16 == 0 then --if i is divisible by 16
s = s .. "\n"
end
--Skip 6 one-byte integers and 2 two-byte integers.
handle:seek("cur", 6 * 1 + 2 * 2)
end
celestia:print(s, math.huge, -1, 1, 1, -1) --upper left corner
handle:close()
wait()
end
main()
On Macintosh and Microsoft Windows, the bytes are reversed.
On Microsoft,
the second argument of
io.open
must be
"rb"
because
the input file is
binarybinary input file.
Do Celestia’s other fonts have other characters?
The
Object:nameObject:name
method of a star returns only the star’s most common name:
Write a program that prints all the names of a star.
The names are listed in the text file
data/starnames.dat,
one star per line.
For example,
The fields are separated by colons.
The first field is the
HipparcosHipparcos catalog
catalog number of the star.
The remaining fields are the names,
often with alternative spellings.
"ALF Ori"
(α
Orionis)
is the
Bayer
designationBayer designation (of star);
"58 Ori"
is the
Flamsteed
designationFlamsteed designation (of star).
The string
line
holds each line of the file,
one by one.
The
patternpattern (Lua)
"[^:]+"
fetches the first field on the line.
The
[[ ] (wildcard in pattern)^^ (in wildcard in pattern):]
is a
wildcardwildcard (in pattern)
that looks for any character that is not a colon.
The
[^:]++ (in pattern)
looks for one or more consecutive characters that are not colons.
Since the pattern tries to be as greedy as possible,
this will grab the entire first field.
The pattern in the
string.gsub
grabs the first field on the line,
plus the colon that separates the first field from the second field,
and removes them.
The remaining fields are names,
processed one by one by the inner loop.
string.gsub("[^:]+:", "", 1) --remove first field
--Loop through the remaining fields.
for name in line:gmatch("[^:]+") do
assert(type(name) == "string")
s = s .. name .. "\n"
end
local duration = 60
celestia:print(s, duration, -1, 1, 1, -1) --upper left
wait(duration)
break --exit from the for loop
end
end
Hipparcos 27989:
Betelgeuse
Betelgeuze
ALF Ori
58 Ori
We will package this code as an “iterator”iterator in createIterator.
The Lua function
errorerror (Lua function)
displays an error message and terminates the Celx program,
but it lets Celestia keep running.
The function accepts one string argument,
to which a newline is appended.
--[[
Call the Lua error function if anything goes wrong.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
--Get permission to mention io.
celestia:requestsystemaccess()
wait()
if io == nil then
error("Cannot demonstrate file input.")
--Don't call wait here, because we never return from error.
end
local handle, message, code = io.open("fonts/default.txf", "r")
if handle == nil then
error("couldn't open file " .. name .. "\n"
.. message .. ", code " .. code)
end
local success, message, code = handle:close()
if success == nil then
error("couldn't close file " .. name .. "\n"
.. message .. ", code " .. code)
end
wait()
end
main()
The Lua
assertassert (Lua function)
function provides
a more compact notation for the
if/then/error/end.
Its second argument defaults to the string
"assertion failed!".
Unfortunately, the second argument of
assert
is evaluated even if the first one is false.
The second argument might be an expensive call to
string.format.
The Standard Library in
stdCelx
therefore calls
error
instead of
assert.
In this book we will often write an
assert
just as concise documentation when introducing a new function,
not because we think there is a realistic chance of failure.
Plentiful examples were in the Lua hooks in
luaHookFunctions.
Where do the
assert
and
error
messages go,
and the similar messages from syntax errors and undefined variables?
On Macintosh,
the messages are written to Celestia’s standard output,
followed by a dramatic
“finis”finis
on the standard error output.
The messages therefore appear only if Celestia is launched from a command line
in the
Terminal
application.
On Microsoft Windows, the error messages appear in a modal dialog box entitled
“Fatal Error”.
On Linux, a Celestia launched from the comand line
will write its error messages to the standard output.
A Celestia compiled
--with-kdeKDE (K Desktop Environment)
will also put up a dialog box with a Details button to display the message.
This civilized behavior is the result of the call to
CelestiaCore::setAlerter
in the constructor for
KdeApp
in
version/src/celestia/kde/kdeapp.cpp.
A Celestia compiled with
--with-glut,
--with-gnome,
or
--with-gtk
will not put up a dialog box.
Instead, it will die with a
SIGSEGVSIGSEGV (signal)
signal
(“Segmentation Faultsegmentation fault (core
dumpedcore dump)”)
because
CelestiaCore::setAlerter
is never called.
Errors and assertions are handled differently
in a callback
(callback),
event handler
(eventHandler),
Lua hook
(luaHookFunctions),
or scripted orbit or rotation
(scriptedOrbit).
In this case the error message is written to the Celestia console
(console),
not to the standard output.
The function that called
error
or
assert
is terminated,
but the rest of the Celx program keeps running.
(A message from a scripted orbit or rotation may disappear into thin air.)
Celestia is implemented with the OpenGL graphics library, a set of functions for drawing 2D and 3D graphics. Some of them can be called directly by a Celx program. We will use them to plot the stars in the Hertzsprung-Russel diagram (loopDatabase), to draw an analemma (Analemma), to lay out the lines on a sundial (Sundial), and to trace the path of a celestial object (project).
Most of the Celx graphics functions are 2D.
In this section,
we will just draw a pair crosshairs on the Celestia window.
For the third dimension,
see the functions
gl.Frustum,
gl.Ortho,
and
glu.LookAt
in
additions.
The OpenGL functions draw on the transparent
overlay
that covers the Celestia window.
To keep the graphics continuously visible,
we will have to redraw them every time the overlay is rendered.
The drawing will therefore have to take place in a tick handler
(tickHandler)
or in the
tick
or
renderoverlay
Lua hooks
(luaHookFunctions).
In this book, we’ll use the
renderoverlay
hook.
To erase the graphics,
the hook can simply return without drawing anything.
The graphics will then disappear in the next sixtieth of a second.
A matrixmatrix (OpenGL) is a rectangle of numbers arranged in rows and columns. OpenGL maintains two stacksstack (OpenGL) of matrices. The matrix at the top of the projection stackprojection stack (OpenGL) controls how the graphics are mapped onto the overlay. We’ll push a plain vanilla identity matrixidentity matrix (OpenGL) onto this stack because we’re doing 2D graphics with no perspective or foreshortening. The matrix at the top of the modelview stackmodelview stack (OpenGL) controls how the graphics are positioned in space. We’ll push another identity matrix to keep the graphics lying flat in the plane of the overlay.
Each push is performed in three steps.
First,
the function
gl.MatrixModegl.MatrixMode
designates the stack onto which the matrix will be pushed.
Then
gl.PushMatrixgl.PushMatrix
pushes a copy of the top matrix onto the stack.
The two top matrices are now identical.
Finally,
gl.LoadIdentitygl.LoadIdentity
changes the top matrix into an identity matrix.
Don’t forget that
the pushed matrix must eventually be popped off the stack.
OpenGL uses its own system of
x,
y
coördinates for the pixels.
The call to
glu.Ortho2Dglu.Ortho2D
sets the
x
coördinates of the overlay’s leftmost and rightmost columns of pixels
to 0 and
width − 1
respectively,
and the
y
coördinates of the bottom and top rows of pixels to 0 and
height − 1.
This means that the origin
(0, 0)
is at the lower left corner of the overlay,
with
x
increasing to the right and
y
increasing upwards.
glu.Ortho2D
modifies the identity matrix we pushed onto the projection stack,
so it must be called while that stack is still the current one.
We don’t have to keep the origin in the lower left corner.
The call to
gl.Translate
moves the origin to the center of the overlay
to make it easier to draw the crosshairs.
The arguments of
gl.Colorgl.Color
specify an rgb color and an alpha level.
With our alpha of .25,
the crosshairs will contribute only .25 of the color of the pixels they occupy,
while the objects covered by the crosshairs will contribute the remaining
1 − .25 = .75
of the color.
These fractions are represented by the constants
gl.SRC_ALPHAgl.SRC_ALPHA
and
gl.ONE_MINUS_SRC_ALPHAgl.ONE_MINUS_SRC_ALPHA.
gl.POINTSgl.POINTS
draws a series of separate points
(loopDatabase),
gl.LINESgl.LINES
a series of separate line segments
(Sundial),
gl.LINE_STRIPgl.LINE_STRIP
a series of connected line segments
(Analemma
and
project),
and
gl.LINE_LOOPgl.LINE_LOOP
a series of connected line segments that returns to its starting point
(loopDatabase).
The following
gl.LINES
must be followed by an even number of vertices.
The
x
and
y
coördinates of the vertices are listed between the
gl.Begin
and
gl.End.
--[[
This file is luahook.celx.
Demonstrate OpenGL graphics by drawing vertical and horizontal crosshairs.
]]
local luaHook = {
renderoverlay = function(self)
--If it is now more than 60 seconds after Celestia started
--running, stop calling this method.
if celestia:getscripttime() > 60 then
self.renderoverlay = nil
return
end
if package.loaded.std == nil then --standard lib not loaded yet
require("std") --not needed yet, but will be later
end
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
--dimensions of the Celestia window, in pixels
local width, height = celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height) --left, right, bottom, top
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
--The default origin (0, 0) is at the lower left corner of the
--window. Move the origin to the center.
gl.Translate(width / 2, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING) --Make text and graphics self-luminous.
gl.Disable(gl.TEXTURE_2D) --disabled for graphics
gl.Color(0, 1, 1, .25) --red, green, blue, alpha
gl.LineWidth(1) --In pixels. Defaults to 1; can have fraction.
gl.Begin(gl.LINES)
--Horizontal crosshair goes
gl.Vertex(-width / 2, 0) --from middle of left edge
gl.Vertex( width / 2, 0) --to middle of right edge.
--Vertical crosshair goes
gl.Vertex(0, -height / 2) --from middle of bottom edge
gl.Vertex(0, height / 2) --to middle of top edge.
gl.End()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
end
}
celestia:setluahook(luaHook)
--[[
Provide an unobtrusive background for the OpenGL graphics.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
wait()
end
main()
In project we will establish a connection between the two-dimensional overlay and the three-dimensional simulated universe beyond it. Until then, the graphics will not be aware of the celestial objects in the universe.
Resize the window by dragging on its lower right corner. Observe that the crosshairs remain centered.
Draw one red pixel at the origin.
Insert the following code immediately after the above
gl.End.
The
gl.POINTS
can be followed by any number of vertices,
but we will follow it with just one.
Draw a green triangle.
Insert the following code immediately after the
gl.End
of the red pixel.
Other simple shapes (square, diamond, triangle)
can be found in the member function
MarkerRepresentation::render
in
version/src/celengine/marker.cpp.
Draw a series of quadrilaterals.
Insert the following code immediately after the
gl.End
of the green triangle.
Let the user drag the triangle with the mouse,
at least if we’re not using Microsoft Windows.
Add the following
x and y fields
(tableOfFields)
to the
luaHook
table:
Add the following
mousebuttonmove
method to the
luaHook
table.
The subtraction is necessary because
the mouse origin is the upper left corner of the overlay
with the Y axis pointing down,
while the
glu.Ortho2D
origin is the lower left corner with the Y axis pointing up.
mousebuttonmove
does not detect a drag in progress on Microsoft Windows;
see
luaHookFunctions.
The vertices of the triangle will now be
gl.Vertex(self.x + 0, self.y + 0) gl.Vertex(self.x + 100, self.y + 0) gl.Vertex(self.x + 100, self.y + 100)Make a circle out of a connected series of lines. The coördinates of each point on the circle will be (rcos θ, rsin θ) for some angle θ.
Insert the following code immediately after the
gl.End
of the green triangle.
The line width of 1.5 comes from the
enableSmoothLines
function in
version/src/celengine/render.cpp.
The value
gl.LINE_LOOP
draws a series of connect line segments returning to the starting point.
Recall that
Celestia:print
(celestiaPrint)
lets us position a string in terms of a whole number of
ems.
The
gl.Translate
function lets us position a string at any pixel in the overlay.
For example,
the first string below has its lower left corner
at the origin in the center of the overlay.
The second string has its center at pixel
(100, 100).
First give the table a field named
font.
local luaHook = {
x = 0, --location of lower left corner of triangle in the window
y = 0,
font = nil,
renderoverlay = function(self)
--etc.
Then initialize the field immediately after
requiring the standard library:
Finally,
insert the following code immediately after the
gl.End
of the circle.
When we print a string,
the first and third arguments of
glu.Ortho2D
must be zero,
and the horizontal and vertical translation in effect
must be numbers that are
1/8
greater than an integer.
The offset of
1/8
ensures that each
texeltexel (texture element)
of a glyph will be
sampled at its middle, not at its edge.
If these rules are violated,
the left and bottom edged of the characters may be sliced off.
The standard library function
gl.TexelRoundgl.TexelRound
rounds its argument to the closest number that is
1/8
greater than an integer.
A tie is rounded up.
See the sundial in
Sundial
for an example.
To measure the translations from the origin,
not from the end of the previous string,
each
gl.Translate
is surrounded by a
gl.PushMatrix
and a
gl.PopMatrix.
The push provides a clean slate for each translation;
the pop discards the slate.
One caveat.
Strings have to be printed one line at a time:
the
newline characternewline (character)
"\n"\n (newline character)
isn’t recognized by OpenGL.
Neither is the
tab charactertab (character)
"\t"\t (tab character)
or the
backspace characterbackspace (character)
"\b"\b (backspace character)
To print the text at an angle, see
glu.LookAtglu.LookAt.
Display an image file,
e.g., the file
textures/logo.pnglogo.png (file)
that comes with Celestia.
In the OpenGL world an image file is called a
texturetexture (OpenGL),
so give the table a field with that name.
Then initialize the field after requiring the standard library:
if package.loaded.std == nil then --standard lib not loaded yet require("std") --initialize self.font here --The filename of the Lua hook file must contain a "/". assert(celestia:getscriptpath():findstring.find("/"))
self.texture = celestia:loadtexture("textures/logo.png")
assert(type(self.texture) == "userdata"
and tostring(self.texture) == "[Texture]")
end
Finally, insert the following code immediately after the last
gl.PopMatrix
of the previous exercise.
The
gl.LINEAR
filter does a better job than the
gl.NEAREST
filter at mapping the pixels of the texture onto the pixels of the overlay.
The method
Celestia:loadtexture
calls the
C++ function
celestia_loadtexture
in
version/src/celestia/celx.cpp,
which looks for a
slashslash (in filename)
in the name of the file containing the Celx code that called
Celestia:loadtexture.
One way to provide the slash is to write the full pathname of the
luahook.celx
file in
celestia.cfg.
A Microsoft Windows pathname has
backslashesbackslash (path component separator),
not slashes,
causing
loadtexture
to print an error message in the Celestia console
(console).
Windows people will therefore have to modify
celestia_loadtexture
and recompile Celestia.
How can we format the digits of an astronomical number? Even more importantly, how many digits are there to format? We raise this issue to forestall any hopeless quest for a level of precision that just isn’t present in the number.
A Celx number is implemented as a C language
“double precision floating point number”,
known familiarly as a
double.
This policy is set by the
LUA_NUMBERLUA_NUMBER (macro)
macros in the
luaconf.hluaconf.h (header file)
header files in the directories
luaversion/src,
version/macosx,
and
version/windows/inc/lua-5.1.
The first macro is the most important.
On my machine, and probably also on yours, a nonzero double holds a value in one of two possible formats. The normalizednormalized (double) format is presented here; the denormalized in denormalized.
A normalized nonzero double holds a value of the form
±
numerator
253
·
2exponent
Let’s look at each piece separately.
The fraction
numerator
253
is called the
mantissamantissa (of double)
of the number.
On my machine, and probably also on yours,
the numerator of the mantissa is an integer in the range
252
= 4,503,599,627,370,496
to
253 − 1 = 9,007,199,254,740,991
inclusive.
These limits make more sense in binary.
252
=
10000000000000000000000000000000000000000000000000000
253 − 1
=
11111111111111111111111111111111111111111111111111111
We can now see that
a numerator is a 53-bit number whose most significant bit is 1.
There are
252
possible values for the numerator,
and the largest one is practically twice as big as the smallest.
The denominator is fixed at 253 = 9,007,199,254,740,992 so the value of the mantissa is in the range 4,503,599,627,370,496 9,007,199,254,740,992 ≤ mantissa ≤ 9,007,199,254,740,991 9,007,199,254,740,992 which we can simplify to .5 ≤ mantissa < 1
The
exponentexponent (of double)
of a double is an integer in the range
–1021
to
1024
inclusive,
with a base of 2.
The values of the numerator, denominator, and exponent of a nonzero double
can be isolated with the Lua function
math.frexpmath.frexp
and the standard library function
std.fractionstd.fraction.
The limits are available as macros
in the C Standard Library header file
float.hfloat.h (header file).
The largest possible normalized double has the largest mantissa and the largest exponent:
253 − 1 253 · 21024 = (253 − 1) · 2971 ≈ 1.79769313486231 · 10308And the smallest positive normalized double has the smallest mantissa and the smallest exponent:
252 253 · 2–1021 = 2–1022 ≈ 2.22507385850720 · 10–308Of greater practical concern is the number of significant decimal digitssignificant digits a double can hold. These are the digits from the leftmost to the rightmost nonzero digits of the double, inclusive. Here is a number with 15 significant digits:
1234567890.12345
A double can always hold at least 15 significant digits,
and sometimes more.
Let’s demonstrate this with the fraction
⅓,
always the acid test of precision.
The double value
closest to
⅓
does indeed have at least 15 threes before it breaks up into garbage.
In fact, it has 16 of them.
6,004,799,503,160,661
253
· 2–1
=
6,004,799,503,160,661
9,007,199,254,740,992
· 2–1
=
6,004,799,503,160,661
18,014,398,509,481,984
= 0.333333333333333314829616256247390992939472198486328125
--[[
Demonstrate that a double can hold at least the first 15 threes of 1/3.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local x = 1/3
local mantissa, exponent = math.frexp(x)
local denominator = 2 ^ std.mantissa
local numerator = math.abs(mantissa) * denominator
local signBit = 0
if x < 0 then
signBit = 1
end
--The numerator and denominator cannot be formatted with %d, even though
--they are integers, because they are greater than or equal to 2^31.
local s = string.format(
"x = %.54f\n"
.. "sign bit = %d\n"
.. "mantissa = %.54f\n"
.. "exponent = %d\n"
.. "numerator of mantissa = %.0f\n"
.. "denominator of mantissa = %.0f\n"
.. "A double with a %d-bit mantissa "
.. "can hold up to %d significant decimal digits.",
x,
signBit, mantissa, exponent,
numerator, denominator,
std.mantissa, std.significant)
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner
wait()
end
main()
The Macintosh output was
x = 0.333333333333333314829616256247390992939472198486328125 sign bit = 0 mantissa = 0.666666666666666629659232512494781985878944396972656250 exponent = -1 numerator of mantissa = 6004799503160661 denominator of mantissa = 9007199254740992 A double with a 53-bit mantissa can hold up to 15 significant decimal digits.The Microsoft Windows output was
x == 0.333333333333333310000000000000000000000000000000000000 sign bit == 0 mantissa == 0.666666666666666630000000000000000000000000000000000000 exponent == -1 numerator of mantissa == 6004799503160661 denominator of mantissa == 9007199254740992 A double with a 53-bit mantissa can hold up to 15 significant decimal digits.
On both platforms,
we will therefore format a double with
string.format
using the
%.15g
format in
floatFormat.
How far apart are consecutive double values? It depends on their size: they get farther apart as they get bigger. Consider the number 2013 = 8,853,267,626,852,352 253 · 211 which belongs to the half-open interval 1024 ≤ x < 2048 The standard notation for this interval is [1024, 2048) and we can write it more simply as powers of 2: [210, 211) The length of the interval is 211 − 210 = 210. There are 252 equally spaced double values that lie in the interval, ranging from 252 253 · 211 = 1024 to 253 − 1 253 · 211 = 2048 – 1 253 These values, all with the exponent 11, divide the interval into 252 equal subintervals. The length of each subinterval is therefore 210 252 = 2–42 = .000000000000227373675443232059478759765625 For example, this length is the distance between 2013 and the next larger and next smaller values that can be stored in a double.
The integer 253 + 1 = 9,007,199,254,740,993 cannot be stored in a double, although its neighbors can.
local x = 2^53 --x can hold 2^53 local y = 2^53 + 1 --y cannot hold 2^53 + 1 local z = 2^53 + 2 --z can hold 2^53 + 2 local s = string.format( "x = %.0f\n" .. "y = %.0f\n" .. "z = %.0f", x, y, z) x = 9007199254740992 y = 9007199254740992 z = 9007199254740994Let’s prove that 253 + 1 is the smallest positive integer that cannot be stored in a double. Consider the half-open interval [253, 254) The length of this interval is 253, and it is divided into 252 equal subintervals by the 252 double values whose exponent is 54. The length of each subinterval is therefore 253 252 = 2 This length is the distance between 253 + 1 and the next larger and next smaller values that can be stored in a double. In the same way, we can prove that the double values in the previous interval [252, 253) are only 1 unit apart from each other, quod erat demonstrandum.
How much precision at interstellar distances do we get from a double? Let’s take BetelgeuseBetelgeuse (star), some 498 lightyears from the Solar System Barycenter in the Celestia universe (643 lightyears in the Wikipedia universe). We will measure the distance to Betelgeuse from the Solar System Barycenter, rather than from the Sun, in order to get the same distance each time.
The
1ee (exponent notation)-6
stands for
--[[
Print the distance in lightyears from the Solar System Barycenter
to Betelgeuse.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local barycenter = celestia:find("Solar System Barycenter")
assert(barycenter:type() == "star" --The barycenter isn't really a star.
and barycenter:getinfo().stellarClass == "Bary")
local betelgeuse = celestia:find("Betelgeuse")
assert(betelgeuse:type() == "star")
--vector pointing from barycenter to Betelgeuse
local toBetelgeuse = betelgeuse:getposition() - barycenter:getposition()
local microlightyears = toBetelgeuse:length()
local mantissa, exponent = math.frexp(microlightyears)
local s = string.format(
"distance in microlightyears = %.15g\n"
.. "distance in lightyears = %.15g\n"
.. "exponent = %d",
microlightyears,
microlightyears * 1e-6,
exponent)
celestia:print(s, 60)
wait()
end
main()
distance in microlightyears = 497964882.348847
distance in lightyears = 497.964882348847
exponent = 29
The Celestia unit of interstellar distance is the microlightyear (linearDistance). In these units, the distance falls into the half-open interval [228, 229) = [268435456, 536870912) The length of this interval is 228, and it is divided into 252 equal subintervals by the 252 double values whose exponent is 29. The length of each subinterval in microlightyears is therefore 228 252 = 2–24 = .000000059604644775390625 A microlightyear is equal to 9,460,730.4725808 kilometers (lightyear), so the length of each subinterval in kilometers is 2–24 · 9,460,730.4725808 = 0.563903479133892059326171875 This roundoff error in our distance to Betelgeuse is only about half a kilometer, vastly smaller than the uncertainty of our knowledge of the distance in the real world. Nonetheless, we will usually print out all 15 significant digits of a double result. We do this to let the reader verify that he or she has exactly duplicated our calculations, not because we claim that our answers are accurate to 15 digits.
How much precision do we get for the star DenebDeneb (star) (α Cygni), 1412 lightyears away in the Celestia universe? For an example with nanometer precision, see positionCoordinates.
The following macro in
float.h
claims that a double can always hold at least 15 significant decimal digits.
DBL_DIGDBL_DIG (macro) 15
Let’s prove it. We will have to show that the double values are more finely grained than the values of numbers with 15 significant decimal digits. In other words, the distance between consecutive double values is less than or equal to the distance between consecutive 15-sigdig numbers.
A positive double x lies in the half-open interval [2y, 2y+1) where y = ⌊ loglogarithm2 x ⌋, the greatest integergreatest integer function that is less than or equal to log2 x. For example, we saw that y = 10 when x = 2013. If x = 2y, the length of this interval is exactly x; and if x > 2y, the length of this interval is less than x. The interval is divided into 252 subintervals by the 252 double values whose exponent is y+1. The length of each subinterval is therefore at most x 252
Now let’s talk about significant decimal digits. A nonzero number with up to 15 significant decimal digits has a value of the following form. ± numerator 1015 · 10exponent The numerator is an integer in the range 1014 = 100,000,000,000,000 to 1015 − 1 = 999,999,999,999,999 inclusive. Thus there are 1015 – 1014 = 9 · 1014 possible numerators. The largest numerator is practically 10 times as big as the smallest one. A positive x lies in the half-open interval [10z, 10z+1) where z = ⌊ log10 x ⌋. (For example, z = 3 when x = 2013.) If x = 10z, the length of this interval is 9x; and if x is slightly less than 10z+1, the length of this interval is slightly greater than .9x. The interval is divided into 9 · 1014 subintervals by the 9 · 1014 numbers with 15 significant decimal digits and the exponent z + 1. The length of each subinterval is therefore always greater than .9x 9 · 1014 = x 1015
So the double values are at least as close together as the 15-sigdig values, because x 252 ≤ x 1015 which is true because 1015 = 1,000,000,000,000,000 ≤ 4,503,599,627,370,496 = 252
A mathematician, by the way, would not be content to state that 1015 ≤ 252. He or she would insist on taking the common logarithm of both sides: 15 ≤ log10 252
[Coda.] Prove that there is no guarantee that a double can always hold 16 significant decimal digits. In other words, prove that the distance between consecutive double values is greater than the distance between consecutive 16-sigdig values. Our mathematician friend would explain this by saying log10 252 < 16
For some calculations Celestia uses a
C language
“single precision floating point”single precision floating point
number,
known familiarly as a
float.
Examples include the
atmosphereCloudSpeed,
albedo,
and
radius
fields in the info tables in
infoTable.
On my machine, and probably on yours,
the parameters in
float.h
for this data type are the following.
Prove that a float can hold at least 6 significant decimal digits,
but not always 7.
Confirm this by checking the macro
FLT_DIGFLT_DIG (macro)
in
float.h.
Hint:
6 ≤ log10 223 < 7
We will therefore format a float with
string.format
using the
%g
format (which means %.6g) in
floatFormat.
We saw in doubleArithmetic that the smallest positive normalized doubledouble precision floating point is 252 253 · 2–1021 = 2–1022 ≈ 2.22507385850720 · 10–308 Even smaller positive values can be stored in a denormalized or subnormal doublesubnormal (double). On my machine, and probably also on yours, a denormalized double has the form ± numerator 253 · 2–1021 The numerator of a denormalized double is an integer in the range 1 to 252 − 1 inclusive. The exponent is fixed at –1021. Thus the smallest positive denormalized double value is 1 253 · 2–1021 = 2–1074 ≈ 4.94065645841247 · 10–324 which is 252 ≈ 4.5 · 1015 times smaller than the smallest positive normalized double. These 15 orders of magnitude will postpone the inevitable day when underflow occurs.
--smallest positive numbers local normalized = 2 ^ (-1021 - 1) local denormalized = 2 ^ (-1021 - 53) local s = string.format( "normalized = %.15g\n" .. "denormalized = %.15g\n" .. "denormalized / 2 = %.15g", normalized, denormalized, --smallest positive value denormalized / 2) --underflow, value is zero normalized = 2.2250738585072e-308 denormalized = 4.94065645841247e-324 denormalized / 2 = 0We saw that a normalized double guarantees 15 significant decimal digitssignificant digitsof precision for any number within its range. Let’s prove that a denormalized double offers no such guarantee. As the numbers get smaller, they suffer a gradual loss of precision.
The distance between consecutive denormalized doubles is 2–1074. Given a positive number x, the distance between the consecutive 15-sigdig numbers closest to x is
x 1015
If we choose x so that
x
1015
<
2–1074
the 15-sigdig numbers will be closer together than the denormalized doubles.
For example, if
x
1015
<
2–1074
≤
x
1014
a denormalized double will be able to hold 14 significant digits of x
but not necessarily 15.
Solving the above inequality for x,
we get
1014
·
2–1074
≤
x
<
1015
·
2–1074
And indeed the following
x
is correct to only 14 digits.
The following value for cos θ is correct to 15 significant digits, and we expect no less. But the value for 1 − cos θ is correct to only 6 significant digits. The next 9 digits are garbageprecision, loss of. What happened?
--[[
Catastrophic cancellation:
cos(theta) is close to 1 for a very small angle theta.
]]
require("std")
local function main()
local observer = celstia:sane()
observer:setposition(std.position)
local theta = math.rad(1 / (60 * 60)) --one second of arc
local s = string.format(
"1 = %.15f\n" --15 dig to right of decimal point
.. "cos(theta) = %.15f\n"
.. "1 - cos(theta) = %.25f computed\n"
.. "1 - cos(theta) = %.25f correct value (to 15 sig digits)",
1,
math.cos(theta),
1 - math.cos(theta),
.0000000000117522152695259)
celestia:print(s, 60)
wait()
end
main()
1 = 1.000000000000000
cos(theta) = 0.999999999988248
1 - cos(theta) = 0.0000000000117522658271696 computed
1 - cos(theta) = 0.0000000000117522152695259 correct value (to 15 sig digits)
The problem is that 1 and cos θ are very close together, differing only in their rightmost five digits. Beyond those digits, the difference is mostly garbage.
Is our angle of 1″ too small to bother with realistically? Not at all. Astronomers regularly deal in milliarcseconds when studying the angular diameter and exoplanets of a star. See the parallax example in parallax.
So how could we compute 1 − cos θ? Let’s find another expression that has the same value, but without having to subtract two very close numbers.
1 − cos θ = (1 − cos θ) · (1 + cos θ) 1 + cos θ = 1 – cos2 θ 1 + cos θ = sin2 θ 1 + cos θThis expression comes out correctly to 15 significant digits.
local s = string.format("1 - cos(theta) = %.25f", math.sin(theta)^2 / (1 + math.cos(theta))) 1 - cos(theta) = 0.0000000000117522152695259Here’s another example where we subtract two very close numbers. Let’s solve the following equation for x, assuming a ≠ 0.
ax2 + bx + c = 0The quadratic formulaquadratic formula gives us two roots.
x1 = –b + b2 − 4ac 2a , x2 = –b − b2 − 4ac 2aIf 4ac is close to zero, then b will be close to b2 − 4ac and catastrophic cancellation will result when we compute x1.
local a = 1 local b = 1 local c = .0000001 --or 1e-7 local r = math.sqrt(b * b - 4 * a * c) local x1 = (-b + r) / (2 * a) local x2 = (-b - r) / (2 * a) local s = string.format( "-b = %.15f\n" .. "r = % .15f\n" --space in place of negative sign .. "-b + r = %.21f computed\n" .. "-b + r = %.21f correct value (to 15 significant digits)\n" .. "x1 = %.21f computed\n" .. "x1 = %.21f correct value (to 15 significant digits)\n" .. "x2 = %.15f computed\n" .. "x2 = %.15f correct value (to 15 significant digits)\n", -b, r, -b + r, -.000000200000020000004, x1, -.000000100000010000002, x2, -.999999899999990)Our value for x2 is correct to 15 significant digits, but –b + r and x1 are correct to only 7.
-b = -1.000000000000000 r = 0.999999799999980 -b + r = -0.000000200000019989766 computed -b + r = -0.000000200000020000004 correct value (to 15 significant digits) x1 = -0.000000100000009994883 computed x1 = -0.000000100000010000002 correct value (to 15 significant digits) x2 = -0.999999899999990 computed x2 = -0.999999899999990 correct value (to 15 significant digits)So how could we compute x1? Let’s find another expression that has the same value, but without having to subtract two very close numbers. x1x2 = –b + b2 − 4ac 2a · –b − b2 − 4ac 2a = b2 − (b2 − 4ac) 4a2 = 4ac 4a2 = c a Therefore x1 = c ax2 Will this give us x1 to 15 decimal places?
In one special case,
Celx uses a different numeric format
to deliver a much higher level of precision.
An object of
class
PositionPosition (class)
(position)
holds the
x,
y,
z
coördinates of a position in the Celestia universe.
Each coördinate is stored in the format
n · 2–64
where
n
is an integer ranging from
–2127
=
–170,141,183,460,469,231,731,687,303,715,884,105,728
≈
–1.70141183460469 · 1038
to
2127 − 1
=
170,141,183,460,469,231,731,687,303,715,884,105,727
≈
1.70141183460469 · 1038
inclusive.
Since the exponent is fixed at
–64,
this format is called
fixed point
as opposed to the
floating point in
doubleArithmetic.
The largest fixed point number has the largest
n:
(2127 − 1)
·
2–64
=
263 − 2–64
=
9,223,372,036,854,775,808
–
1
18,446,744,073,709,551,616
=
9,223,372,036,854,775,807.9999999999999999999457898913757247782996273599565029144287109375
The smallest positive fixed point number has the smallest positive
n:
1 · 2–64
=
1
18,446,744,073,709,551,616
=
.0000000000000000000542101086242752217003726400434970855712890625
≈
5.42101086242752 · 10–20
And the closest fixed point number to
⅓
has 19 threes before it breaks up into garbage:
6,148,914,691,236,517,205
· 2–64
=
6,148,914,691,236,517,205
18,446,744,073,709,551,616
= 0.3333333333333333333152632971252415927665424533188343048095703125
That’s three orders of magnitude—a thousand times—more
precise than the double value of
⅓,
which had only 16 threes in
doubleArithmetic.
How much precision do we get from a fixed point number in the Celestia universe? The unit of distance is the microlightyear, equal to 9,460,730.4725808 kilometers (lightyear). The distance in kilometers between positions represented by consecutive fixed point values is therefore 1 · 2–64 · 9,460,730.4725808 = 9,460,730.4725808 18,446,744,073,709,551,616 ≈ 5.12867226583596 · 10–13 That’s 5.12867226583596 · 10–10 meters, or a little more than half a nanometernanometer. (One nanometer equals 10–9 meters.)
How many lightyears does the biggest fixed point number represent? Is it adequate for the radius of the observable universeobservable universe (currently 46 billion lightyears)?
Celestia’s units range from pixels to parsecs. Pixels belong to real space; parsecs to simulation space. There are also units of angular distance, mass, time, temperature, and flux.
The
speed of lightlight, speed of
is 299,792,458 meters per second.
The number of
meters
in a
lightyearlightyear
is therefore
299,792,458 · 60 · 60 · 24 · 365.25
= 9,460,730,472,580,800
which works out to
9,460,730,472,580.8
kilometers
or approximately
.306601393785551
parsecs
(parsec).
When the number of kilometers
is stored as a single precision floating point number
(doubleArithmetic),
it is rounded to
9,460,730,822,656.
An example is the default value of
Object:radius
for a deep sky object.
The position of an observer or a celestial object is measured in
microlightyearsmicrolightyear.
A microlightyear is a millionth of a lightyear, a mere
9,460,730.4725808
kilometers.
This number is stored in the predefined global variable
KM_PER_MICROLYKM_PER_MICROLY (Celx variable),
uppercase with underscores.
Older versions of Celestia thought a lightyear was 9,466,411,842,000 kilometers, a value that still lurks in the source code in more than one place. Verify that it resulted from swapping two adjacent digits in the speed of light in kilometers per second.
The average distance from the
Sun
to the
Earth
is called an
astronomical unit.
Celestia uses the value
149,597,870.7 kilometers in
version/src/celengine/astro.h,
available in the standard library as
std.kmPerAustd.kmPerAu.
It is equivalent to roughly 16 microlightyears
(std.microlyPerAustd.microlyPerAu).
Astronomical units are used in the
.ssc
files for the orbits of planets, asteroids, and comets,
but not for the satellites of the planets.
A
parsec
is the distance from the Sun to an object whose
annual parallaxparallax
is
1″
(one second) of arc.
The angle is exaggerated in the following diagram.
In terms of astronomical units,
1 parsec =
1
sinsine (trig function) 1″
au
≈
206,264.806247905 au
This works out to approximately
3.26156377790433 lightyears
(std.lyPerPcstd.lyPerPc)
or
30,856,775,821,885.3
kilometers
(std.kmPerPcstd.kmPerPc).
To approximate a parsec without computing sine, recall that the graph of sine goes through the origin at a 45° angle.
Thus for a tiny angle of θ radians we have sin θ ≈ θ Our angle of 1″ is equal to 2π 360 · 60 · 60 radians so sin 1″ = sin ( 2π 360 · 60 · 60 radians) ≈ 2π 360 · 60 · 60 Therefore 1 parsec ≈ 360 · 60 · 60 2π au ≈ 206,264.806272689 au which is correct to 10 significant digits.
Ancient versions of Celestia had an origin
one
milliparsec
(about 206 astronomical units)
from the Sun;
see
universalFrame.
The milliparsec still shows up when we press the
Follow Earth button in a Celestia compiled
--with-kdeKDE (K Desktop Environment).
Intraplanetary distances are in kilometers:
local earth = celestia:find("Sol/Earth") local radius = earth:radius() --in kilometers local info = earth:getinfo() --a table of fields radius = info.radius --in kilometers, the same number local atmosphereHeight = info.atmosphereHeight --in kilometers local atmosphereCloudHeight = info.atmosphereCloudHeight --in kilometersThe radius of a spacecraft is in kilometers. Multiply it by 1000 to convert to meters.
local cassini = celestia:find("Sol/Cassini") local s = string.format("Cassini radius = %g meters", 1000 * cassini:radius()) Cassini radius = 11 metersThe radius of a deep sky object (a galaxy, globular cluster, open cluster, or nebula) is available in kilometers or lightyears:
local dso = celestia:find("Milky Way") local kilometers = dso:radius() local lightyears = dso:getinfo().radius --not microlightyearsThe distance between two objects is available in kilometers or microlightyears:
local earth = celestia:find("Sol/Earth") local earthPosition = earth:getposition() --position of center local moon = celestia:find("Sol/Earth/Moon") local moonPosition = moon:getposition() --distance in kilometers local kilometers = earthPosition:distanceto(moonPosition) --a vector pointing from center of Earth to center of Moon local vector = moonPosition - earthPosition --the same distance, but in microlightyears local microlightyears = vector:length()
Kilometers are used for the distance argument of
Observer:gotolonglat
and
Observer:gotodistance.
The kilometer was originally defined as 1/40000 of the polar circumferenceEarth, circumference of the Earth.
local earth = celestia:find("Sol/Earth") local r = earth:radius() --in kilometers local circumference = 2 * math.pi * r local s = string.format("circumference = %.15g km", circumference) circumference = 40075.0363941636 km
Can we make the error smaller?
The Earth is actually shaped like an
oblate
spheroidoblate spheroid (shape of Earth),
bulging at the equator.
In cross section it is an
ellipseellipse, as cross section of oblate spheroid
whose
semi-majorsemi-major axis (of ellipse)
and
semi-minorsemi-minor axis (of ellipse)
axes are the following
a
and
b.
There is—surprisingly—no simple formula
for the
circumference
of an ellipse,
but the following
for
loop gives us a good approximation.
For the remaining sources of error, see Ken AdlerAdler, Ken, The Measure of All ThingsMeasure of All Things, The (Adler): The Seven-Year Odyssey and Hidden Error That Transformed the World. To land a spacecraft on the surface of an oblate spheroid, see geodetic.
Measurements in
pixels
belong to the domain of the real space of the user,
not the simulation space of the observer
(universalFrame).
Celestia assumes that the screen has 96 pixels per inch
(std.pixelsPerInstd.pixelsPerIn).
The dimensions of the window are in pixels;
see
Celestia:getscreendimension
(celestiaPrint
and
windowDimensions)
and the
resize
Lua hook
(luaHookFunctions).
Together with the user’s default distance of 400 millimeters
from the screen,
these dimensions determine the user’s field of view
in real space
(std.getverticalfov
and
std.gethorizontalfov).
With the observer’s level of
magnification,
we can then determine the observer’s
field of view
in simulation space
(Observer:getverticalfov
and
Observer:gethorizontalfov).
One
inch,
by the way, equals 25.4 millimeters
(std.mmPerInstd.mmPerIn).
One
mile
equals 5280 feet
(std.ftPerMilestd.ftPerMile).
Fonts, strings, and marks are measured in pixels, not
pointspoint (font size);
see
Celestia:gettextwidth,
Font:getwidth,
Font:getheight,
and
Object:mark.
One full turn is divided into 360
degreesdegree (of arc)
of arc.
Each degree is divided into 60
minutesminute (of arc),
and each minute into 60
secondssecond (of arc).
Thus,
1° = 60′ = 3600″
A
milliarcsecond
is a thousandth of second.
Celestia uses degrees for the field of view in a
cel:
URL;
see
Celestia:geturl.
The angle through which the Earth rotates during a given period of time
may be described as 0 to 360 degrees, or as
0 to 24
hourshour (of right ascension)
of
right
ascension.
In this system,
24h
=
360°
1h
=
15°
Dividing both sides by 60,
we see that a
minuteminute (of right ascension)
of right ascension is 15 times bigger than a minute of arc:
1m
=
15′
Another division by 60 shows that a
secondsecond (of right ascension)
of right ascension
is 15 times bigger than a second of arc.
1s
=
15″
We also give another interpretation to right ascension, thinking of it as the angle through which the Universe rotates around a stationary Earth. See j2000Equatorial.
An angle can also be measured in radians. One full turn is divided into 2π radians, so 2π radians = 360°
We use 2π because it is the circumference of the unit circle, whose radius is 1. The size in radians of an angle is equal to the length of the portion of the circumference that is subtended by the angle. For example, an angle of 2π radians goes all the way around the circumference.
ππ (mathematical constant)
is approximately
3.14159265358979
and is available as
math.pimath.pi.
local circumference = math.pi * diameter
Here are the conversion factors, to 15 significant digits.
1 radian = 180 π degrees ≈ 57.2957795130823° ≈ 57° 17.7467707849393′ ≈ 57° 17′ 44.8062470963552″Lua provides two conversion functions.
local radians = math.radmath.rad(degrees) --Convert degrees to radians.
local degrees = math.degmath.deg(radians) --Convert radians to degrees.
All Lua trig functions are in radians.
local s = math.sinmath.sin(radians) --Argument of sin is in radians.
local radians = math.asinmath.asin(s) --Return value of arcsin is in radians.
Celx functions and fields are in radians too.
--vertical field of view of window local observer = celestia:getobserver() local radians = observer:getfov() --Return value is in radians. observer:setfov(radians) --Argument is in radians. local object = celestia:find("Sol/Earth") local info = object:getinfo() local radiansPerDay = info.atmosphereCloudSpeedatmosphereCloudSpeed (info table field)
local s = ""
if radiansPerDay ~= nil then
s = string.format("Cloud speed = %g degrees per day.",
math.deg(radiansPerDay))
if radiansPerDay ~= 0 then
s = s .. string.format(
"\nThe clouds take %g day(s) to circle %s.",
2 * math.pi / radiansPerDay, object:name())
end
end
Cloud speed = 65 degrees per day.
The clouds take 5.53846 day(s) to circle Earth.
The Celx Standard Library functions (standard) are in radians.
--[[ latitude is in radians: positive for north, negative for south. lat is a table containing four fields, direction is a table containing two fields. ]] local lat = std.tolat(latitude) local direction = {[1] = "North", [0] = "", [-1] = "South"} local s = string.format( "Latitude %d degrees %d minutes %.15g seconds %s", lat.degrees, lat.minutes, lat.seconds, direction[lat.signum]) --longitude is in radians: positive for east, negative for west. --long is a table containing four fields. local long = std.tolong(longitude) local direction = {[1] = "East", [0] = "", [-1] = "West"} local s = string.format( "Longitude %d degrees %d minutes %.15g seconds %s", long.degrees, long.minutes, long.seconds, direction[long.signum]) --rightAscension is in radians, e.g. pi radians = 12 hours. --ra is a table containing three fields. local ra = std.tora(rightAscension) local s = string.format( "Right Ascension %d hours %d minutes %.15g seconds", ra.hours, ra.minutes, ra.seconds) --declination is in radians, e.g. pi/2 radians = 90 degrees. --dec is a table containing four fields. local dec = std.todec(declination) local s = string.format( "Declination %s%d degrees %d minutes %.15g seconds", std.sign(dec.signum), dec.degrees, dec.minutes, dec.seconds)
See
time
for the difference between simulation time and real time.
Simulation time is measured in Earth days,
starting with the methods
Celestia:gettime
and
Celestia:settime.
This type of day is the
mean
solar daymean solar day
of 24 hours,
not the
sidereal daysidereal day
of 23 hours, 56 minutes, 4 seconds.
Intervals of real time are measured in seconds,
starting with the return value of
Celestia:getscripttime.
A second is
1
60 · 60 · 24
=
1
86,400
of a day.
The method
Celestia:getsystemtime
returns the current real time,
not the length of an interval,
so its return value is in days.
The
dimensionlessdimensionless quantity
ratio between simulation time and real time
is manipulated with
Celestia:gettimescale
and
Celestia:settimescale.
See
settime.
Temperature is measured in degrees KelvinKelvin (unit of temperature). To convert Kelvin to CelsiusCelsius (unit of temperature), subtract 273.15. To convert Celsius to Fahrenheit, multiply by 212 − 32 100 − 0 = 9 5 and add 32.
The temperature of a star can be read from the
temperature
field of the star’s info table.
See
infoTable.
The temperature of a non-luminous body can be displayed when
Celestia is set to
verbose mode.
On Macintosh,
Celestia →
Preferences… →
General →
Info Display
On Microsoft Windows,
Render →
View Options… →
Information Text
Then select the body as in
keystroke.
The
luminosity
field of the info table
(infoTable)
of a star is measured in multiples of the
Sun’s
luminositySun, luminosity of.
This value is
3.8462 · 1026
watts
in
version/src/celengine/astro.cpp.
The
mass
field of the info table
of an
extrasolar
planetextrasolar planet
is measured in multiples of the
mass
of the
EarthEarth, mass of.
This value is
5.976 · 1024
kilograms
in
version/src/celengine/astro.cpp.
JupiterJupiter, mass of,
to which extrasolar planets are often compared,
is approximately 318 times as massive as the Earth.
The
atmosphereCloudSpeed
field of the info table of a planet or moon
is measured in
radians
per day.
(The corresponding field in a
.ssc
file is in degrees per day.)
The argument of
Observer:setspeed
is in microlightyears per second of real time.
The fifth argument of
Celestia:print
is in
emsem (unit of width)
(the width of an uppercase letter M).
Some measurements are
dimensionlessdimensionless quantity
because they are the ratios of two measurements with the same units.
These include the
albedo
and
oblateness
fields of the info table,
the timescale between the simulation time and the real time,
the
Eccentricity
field of an
EllipticalOrbit
in
data/solarsys.ssc,
the magnification passed to
Observer:setmagnification
in
Magnification,
and the
Rayleigh, absorption, and Mie coefficients
passed to
Object:setatmosphere.
A mathematical purist would also say that an angle in
radiansradian
is dimensionless.
Some measurements are downright subjective.
Consider the
importance
field of the info table of a location:
is the second most important world capital really
SeoulSeoul, South Korea?
Formatting a value means rendering it as a humanly-readable string of characters. For example, an integer (whole number) can be formatted in decimal or hexadecimal, and any number can be formatted in scientific notation or in the plain old notation. a string can be left or right justified. A date or time can be formatted as in tdb. For colors, see integerFormatting.
This section assume that we have a normal Celx number.
To print a fixed point number in a
Position
object,
see
bits128.
By default,
a number is converted into a string with 14 significant decimal digits.
The conversion can be performed in two ways:
explicitly,
by the Lua function
tostringtostring (Lua function);
or implicitly,
by
concatenation
to an existing string.
The existing string can even be the
null string
"".
--[[
Demonstrate the default format (14 significant digits)
in which a number is rendered as a string.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local n = 1234567890.12345 --15 significant decimal digits
local explicit = tostring(n) --explicit conversion to string
local implicit = n .. "" --implicit conversion to string
celestia:print(explicit .. "\n" .. implicit, 60)
wait()
end
main()
1234567890.1235
1234567890.1235
These 14 digits are one less than the 15 digits guaranteed by a double in
doubleArithmetic.
The culprit is the
“number format”
macro in the header file
luaversion/src/luaconf.hluaconf.h (header file).
LUA_NUMBER_FMTLUA_NUMBER_FMT (macro) "%.14g"
The Lua function
string.formatstring.format
gives us control over how a number is formatted.
For example, it can wring out all 15 significant digits of a double,
or round the double to fewer decimal places.
The function accepts the same
% formats% format (string.format)
as the C function
printfprintf (C function).
Let’s start with the integers.
The format
%d
prints in decimal.
An optional number before the
%d
specifies the minimum number of characters to be output;
a narrower number will be padded with leading blanks or a zeroes.
The format
%d
prints a negative number with a minus sign,
but a positive number with no plus sign.
To print every value with an explicit sign,
use
%+d.
(Zero will have a plus sign.)
Print an integer
in base 10 with %d,
in base 8 with %o,
and in base 16 with %X or %x
(upper or lowercase).
string.gsub("%d", octalToBinary) --"11011110101011011011111011101111"
The format
%u
stands for
“unsigned”unsigned number.
It prints an integer in base 10,
adding
231 = 2,147,483,648
if necessary to make the integer nonnegative.
See
inputFile.
The
%d
cannot be used for an integer greater than or equal to
231 = 2,147,483,648
or less than
–231
= –2,147,483,648.
An integer in the range
231
to
232 − 1 = 4,294,967,296
inclusive can be formatted with
%u,
%o,
%X,
or
%x.
An integer greater than or equal to
231
can a be formatted as a float
(floatFormat)
with no digits to the right of the decimal point.
Verify that the above example can also be written as follows. The parentheses around the string are required. Which way is easier to understand?
local i = 2^32 local s = ("%.0f"):format(i) --"4294967296"
The format
%f
prints a number with a fraction,
by default with six digits to the right of the decimal point.
A number before the
%f
specifies the minimum number of characters to be output.
The number after the dot specifies
the number of digits to the right of the decimal point.
The format
%e
delivers
scientific notation,
by default with six digits to the right of the decimal point.
The format
%g
behaves like
%e
or
%f,
depending on the magnitude of the value.
The number after the dot specifies the total number of significant digits
to be printed.
To print the entire value,
with no advance knowledge of its magnitude,
your best bet is
%.15g.
Format a string of characters with
%s.
To add
quotesquotes around string
to the string, see the
%q
in
standard.
Astronomical writing is full of special characters,
starting with the symbols for degrees, minutes, and seconds:
1° 2′ 3″.
Although it might be possible to write these characters
in the source code of a Celx program,
such usage is platform dependent.
A portable way to represent a special character is via its
UnicodeUnicode character
number in the
code charts
at
www.unicode.org.
For example, the code number of the degree symbol °
is
176 in decimal
and
00B0 in hexadecimal.
To display the code number of every character in a font,
see
inputFile
A Unicode number is written as a four-digit hexadecimal number,
with a leading
0x
(zero lowercase X)
in Celx to indicate its base.
To print the corresponding character,
the number must be broken down into a series of 8-bit bytes in
UTF-8UTF-8 (character encoding)
format,
and then pasted back together with the Lua function
string.charstring.char.
For example,
the following
0x03B1
(the code number of the lowercase Greek letter
α)
must be broken into
0xCE
and
0xB1
before it can be reconstituted as a one-character string.
An easy way to convert a Unicode number into a one-character string
is with the function
std.utf8std.utf8.
Even easier,
the table
std.charstd.char
contains fields for the most common special characters.
--[[
Print a special character.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
--Three ways to print Greek lowercase alpha (Unicode 03B1).
local s = string.char(0xCE, 0xB1) .. "\n" --hard
.. std.utf8(0x03B1) .. "\n" --easier
.. std.char.alpha .. "\n" --easiest
.. std.char.alpha .. " Orionis (Betelgeuse), Declination "
.. 7 .. std.char.degree .. " "
.. 24 .. std.char.minute .. " "
.. 25 .. std.char.second .. " North"
local duration = 60
celestia:print(s, duration)
wait(duration)
end
main()
α
α
α
α Orionis (Betelgeuse), Declination 7° 24′ 25″ North
The string can also be composed with
string:format
(stringFormat).
A Celx variable can refer to an object,
as we saw in
objectsVsVariables.
These objects fall into two groups.
A
Lua objectLua object
is inherited from the language Lua
and represents a computer science concept
such as a string or an array.
A
Celx objectCelx object
is unique to Celx
and represents a mathematical or astronomical concept
such as a vector or a planet.
To tell them apart,
call the Lua function
typetype (Lua function).
A Celx object belongs to one of the twelve
classesclass of Celx object
in
additions.
Call the Lua function
tostringtostring (Lua function)
to find out which one.
The name of the class begins with an uppercase letter.
We will ignore the
[square brackets].
A Celx object belonging to class
Object
(i.e., class "[Object]")
represents a celestial object such as a planet, spacecraft,
or even a city or crater.
To get a celestial object from one of Celestia’s databases,
call the method
Celestia:findCelestia:find
with an argument such as one of the following.
The argument is case-insensitive,
but any chunk of whitespace in the argument must consist of exactly one space.
"Sol"
"Sol/slash (in name of celestial object)Earth" (a
planet in our solar system)
"Sol/Earth/Moon"
"Sol/Earth/Moon/Mare Tranquillitatis"
"Pollux"
"Pollux/b" (a planet in another solar system)
Celestia:find
returns a Celx object of class
Object.
The method
Object:name
returns the rightmost segment of the object’s name
(e.g., the
"Moon"
of
"/Sol/Earth/Moon"),
excluding the slashes and the characters to the left of any slash.
The method
Object:typeObject:type
returns a string giving the object’s astronomical classification,
such as
"planet",
"star",
or
"comet".
If
Celestia:find
cannot find the celestial object,
its behavior will depend on whether the standard library has been
required.
If the library has been required,
Celestia:find
will call the Lua function
errorerror (Lua function)
with the message
“Celestia:find could not find "<name>"”.
And as we know,
error
never returns.
If the library has not been required,
Celestia:find
will return a dummy object whose
name and type are the strings
"?"
and
"null" respectively.
(If the library has been required,
and a dummy object is desired as the result of an unsuccessful search,
call
Celestia:oldfind.)
Every celestial object has an “info table” of information
(infoTable)
The object’s name and type are also present as fields in the info table.
The dummy object has an info table with no
name
field,
and a
type
field whose value is the string
"null".
By default,
a
goto
takes five seconds of real time,
available as the constant
std.duration.
To ensure that nothing else happens while the
goto
is in progress,
we can
wait
(wait)
for the same number of seconds.
--[[
Find a celestial object in Celestia's database.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local name = "Sol/Mars"
local object = celestia:find(name)
--This is the check that Celestia:find does for us automatically,
--since we required std.
--[[
if type(object) ~= "userdata"
or tostring(object) ~= "[Object]"
or object:type() == "null"
or object:name() == "?" then
error("Celestia:find could not find \"" .. name .. "\"")
end
]]
celestia:select(object) --display distance, radius, etc.
local s = string.format(
"type(object) = %s\n"
.. "tostring(object) = %s\n"
.. "object:name() = %s\n"
.. "object:type() = %s\n",
type(object), tostring(object),
object:name(), object:type())
celestia:print(s, 60, -1, 1, 1, -6) --below selected object info
observer:goto(object) --go to a point 5 radii from the object's center
wait(std.duration) --the number of seconds that the goto takes
end
main()
type(object) = userdata
tostring(object) = [Object]
object:name() = Mars
object:type() = planet
We have just seen two
types:
the Lua function
type
and the
type
method of class
Object.
There is also
a Lua function named
typeio.type
that checks if a file is currently open
(inputFile),
and a field named
type
in a celestial object’s info table
(infoTable)
and in the table passed to the method
Object:addreferencemark.
The prefix
"Sol/"
in the above
"Sol/Mars"
was unnecessary,
since Sol is the star of the solar system closest to the observer.
Verify that the
"Sol/"
becomes necessary if the observer has first gone to Betelgeuse:
--Go to a position 100 Betelgeuse radii from center of Betelgeuse.
local betelgeuse = celestia:find("Betelgeuse")
observer:goto(betelgeuse)
wait(std.duration)
celestia:find("Mars") --Now find calls the error function.
If we go from the standard position to the Sun,
local observer = celestia:sane()
observer:setposition(std.position)
local object = celestia:find("Sol")
observer:goto(object)
wait(std.duration)
the
Observer:goto
makes a terrifying plunge towards the solar surface.
To diagnose this,
we have to know that every type of celestial object has a
preferred distancepreferred distance.
For a planet, the distance is five times the radius.
For a star,
it’s 100 times the radius,
as in the previous exercise.
If we are already closer than the preferred distance,
a
goto
takes us 10 times closer than our current distance.
(Warning.
The preferred distance for a
black hole
is 100 times the radius.)
To go to an explicit distance from the object,
call the method
Observer:gotolonglatObserver:gotolonglat.
Call
math.rad
to convert the longitude and latitude to radians.
Check that all of the following find the same star. Each chunk of whitespace must be exactly one space.
--Arabic name local name = "Betelgeuse" local name = "betelgeuse" --case insensitive local name = "Betelgeuze" --alternative spelling --Bayer designation: name of constellation in Latin genitive case local name = "Alpha Orionis" local name = "Alpha Ori" local name = "ALF Ori" local name = std.char.alpha .. " Orionis" --Flamsteed designation local name = "58 Orionis" local name = "58 Ori" --catalog numbers local name = "HIP 27989" --Hipparcos local name = "HD 39801" --Henry Draper local name = "SAO 113271" --Smithsonian Astrophysical Observatory
The method
Object:nameObject:name
returns only one of the names of a star.
It prefers to return a name in Arabic, Latin, Greek, or even English
(try
"The Garnet Star").
Otherwise it returns the
BayerBayer designation (of star)
or
Flamsteed
designationFlamsteed designation (of star).
As a last resort,
it returns one of the catalog numbers:
HipparcosHipparcos catalog,
Henry
DraperHenry Draper catalog,
or
Smithsonian
Astrophysical ObservatorySmithsonian Astrophysical Observatory catalog.
To get all the names of a star,
see
inputFile.
Lua’s only data structure is the
tabletable (Lua),
an associative array or
hash
of
key/value pairskey/value pair.
We look up a
key
in a table to find the corresponding
value.
The following table is named
zodiac.
Its keys are not explicitly specified,
so they default to increasing consecutive integers starting at 1.
A table with these keys is called an
arrayarray (Lua table)
or a
sequencesequence (Lua table);
see the Lua documentation for the fine points.
The operator
## (highest key operator)
returns the highest key in the array,
which is the number of key/value pairs.
(In Lua 5.2, this operator has replaced the function
table.maxn.)
The value corresponding to each key in the following table is a string.
There are two ways to loop through an array:
with a numeric
for
loopfor loop,
or with a generic
for
loop and the Lua function
ipairsipairs (Lua function).
The generic loop calls
ipairs
once.
The return value is another function, called an
iteratoriterator.
We never see this iterator,
but it is called over and over by the loop.
Each call returns the next key/value pair from the array.
When a call returns
nilnil (Lua value),
the loop terminates.
The first three arguments of
Celestia:setconstellationcolorCelestia:setconstellationcolor
are the red, green, and blue components of the color, in the range 0 to 1.
We’ll use the rgb values in the
Renderer::EclipticColorRenderer::EclipticColor (C++ constant)
in
version/src/celengine/render.cpp.
The optional fourth argument
is an array of constellation names.
--[[
Create and print an array of strings.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local zodiac = { --Curly braces create a table.
"Aries", --Key is 1, value is "Aries".
"Taurus", --Key is 2, value is "Taurus".
"Gemini",
"Cancer",
"Leo",
"Virgo",
"Libra",
"Scorpius",
"Sagittarius",
"Capricornus",
"Aquarius",
"Pisces" --Key is 12, value is "Pisces".
}
assert(type(zodiac) == "table" and #zodiac == 12)
local s = string.format(
"The zodiac has %d constellations, from %s to %s:\n\n",
#zodiac,
zodiac[1][ ] (subscripting operator), --Look up first key & get corresponding value.
zodiac[#zodiac]) --Look up last key & get corresponding value.
--Two ways to do the same loop.
--numeric for loop
for i = 1, #zodiac do
s = s .. i .. " " .. zodiac[i] .. "\n"
end
s = s .. "\n" --Skip a line between the two lists.
--generic for loop
assert(type(ipairs) == "function")
assert(type(ipairs(zodiac)) == "function") --An iterator is a function.
for i, value in ipairs(zodiac) do
s = s .. i .. " " .. value .. "\n"
end
celestia:setconstellationcolor(.5, .1, .1, zodiac) --rgb
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner of window
wait()
end
main()
The zodiac has 12 constellations, from Aries to Pisces:
1 Aries
2 Taurus
3 Gemini
4 Cancer
5 Leo
6 Virgo
7 Libra
8 Scorpius
9 Sagittarius
10 Capricornus
11 Aquarius
12 Pisces
1 Aries
2 Taurus
3 Gemini
4 Cancer
5 Leo
6 Virgo
7 Libra
8 Scorpius
9 Sagittarius
10 Capricornus
11 Aquarius
12 Pisces
Number the constellations from 0 to 11.
Since
ipairs
always starts at 1,
we will have to do the counting with a numeric
for
loop.
A
two-dimensional arrayarray, two-dimensional
is implemented as an “array of arrays”,
created with nested curly braces.
Each column can be a different data type.
The fourth argument of
Celestia:setconstellationcolor
must be an array of strings.
In this case it is a very short array,
consisting of only one string.
local zodiac = {
--name r g b
{"Aries", 255, 0, 0}, --red
{"Taurus", 255, 127, 0}, --orange
{"Gemini", 255, 255, 0}, --yellow
{"Cancer", 0, 255, 0}, --green
{"Leo", 0, 0, 255}, --blue
{"Virgo", 75, 0, 130}, --indigo
{"Libra", 127, 0, 255}, --violet
--etc.
}
assert(type(zodiac) == "table" and #zodiac == 12)
local s = string.format(
"The zodiac has %d constellations, from %s to %s.\n"
.. "The amount of red in the first constellation is %d.",
#zodiac,
zodiac[1][1], --Can apply 2 subscripts to a 2-dimensional array.
zodiac[#zodiac][1],
zodiac[1][2])
for i, value in ipairs(zodiac) do
assert(type(value) == "table" and #value == 4)
celestia:setconstellationcolor(
value[2] / 255,
value[3] / 255,
value[4] / 255,
{value[1]}) --Curly braces create a table.
end
A
moving
groupmoving group (of stars)
is a group of stars that move together.
Let’s mark the core stars of the
Ursa Major
Moving GroupUrsa Major Moving Group.
The third argument of
Object:mark
is the size in pixels of the marker symbol.
The fourth argument is the alpha level.
--An array that contains strings:
--the names of the core stars of the Ursa Major Moving Group.
local group = {
"Alcor", --bound to Mizar
"Alioth", --Epsilon Ursae Majoris
"Merak", --Beta Ursae Majoris, one of the Pointers
"Megrez", --Delta Ursae Majoris, joins bowl to handle
"Mizar A", --Zeta Ursae Majoris
"Mizar B",
"Phecda", --Gamma Ursae Majoris
"78 UMa",
"37 UMa",
"HIP 64532", --Hipparcos catalog number
"HIP 61100",
"HIP 61946",
"HIP 61481" --in Canes Venatici
}
--[[
Face Megrez in the Big Dipper. Orient the observer so that Megrez is in
the center of the window, and the line from Megrez to the north pole of
the ecliptic in Draco points straight up towards the top of the window.
]]
local megrez = celestia:find("Megrez")
local position = megrez:getposition()
observer:lookatObserver:lookat(position, std.yaxis)
for i, name in ipairs(group) do
local star = celestia:find(name)
star:mark("green", "diamond", 10, .9, star:name())
end
Let the size of the marker show the distance to the star. local position1 = observer:getposition() local position2 = star:getposition() local distance = position1:distanceto(position2) --in kilometers star:mark("green", "diamond", distance / 7e13, .9, star:name()) Are all the stars at approximately the same distance from us? What about the seven stars that form the Big DipperBig Dipper?
The Virgo ClusterVirgo Cluster (of galaxies) is the cluster of galaxiesgalaxy cluster at the heart of the Virgo SuperclusterVirgo Supercluster. Look at its most prominent member, the giant galaxy M87M87 (galaxy) in VirgoVirgo. Then mark the 16 Messier objectsMessier object that belong to the cluster.
--Zoom in to prevent the labels from stepping on each other. observer:setfov(math.rad(16)) --[[ The keys in this array are numbers. The values are numbers too. The values are the numbers of the Messier objects in the Virgo Cluster. ]] local messier = { 49, --M49, elliptical. 58, --spiral 59, --elliptical 60, --elliptical 61, --spiral 84, --lenticular 85, --lenticular 86, --lenticular 87, --giant elliptical 88, --spiral 89, --elliptical 90, --spiral 91, --barred spiral 98, --spiral 99, --spiral 100 --spiral } for i, m in ipairs(messier) do --one space after the uppercase M local name = string.format("M %d", m) --etc. endThe keys in the next array are still integers, but now the values are celestial objects.
Human beings like to see their numbers right justified
and their strings left justified.
A positive width such as
%2d
will right justify,
and a negative width such as
%-9s
will left justify.
Of course, the columns will line up only if the font is monospace.
--[[
Print a table of celestial objects: the moons of NeptuneNeptuneNeptune
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local neptune = celestia:find("Sol/Neptune")
local children = neptune:getchildren() --an array of celestial objects
assert(type(children) == "table")
local s = ""
for i, child in ipairs(children) do
assert(type(child) == "userdata"
and tostring(child) == "[Object]")
s = s .. string.format("%2d %-9s %6.1f (%s)\n",
i, child:name(), child:radius(), child:type())
end
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner of window
wait()
end
main()
GalateaGalatea (moon of Uranus)
is a minor moon even though it’s bigger than
LarissaLarissa.
See the comment at the start of
data/solarsys.sscsolarsys.ssc (file).
A recursive data structure contains subparts with the same structure as the whole. An example is the family tree of the Sun, containing trees within trees within trees. The simplest way to traverse a recursive data structure is with a recursive function, one that calls itself.
Let’s write a recursive function
that will print the entire tree rooted at the Sun,
one object per line.
The planets will be indented by one pair of spaces,
their satellites by two pairs of spaces,
and the satellites of the satellites by three pairs of spaces.
The pair of spaces is written as a
string literalliteral
(a value in double quotes:
" ").
To make the literal count as an object with methods,
we have to enclose it in parentheses.
To create multiple copies of this object,
we call the Lua method
string.repstring.rep
(“replicate”).
Celestia:print
will print no more than
210 − 1
= 1023
characters of a string;
see
celestiaPrint.
The
string:substring.sub
method returns a prefix of this length.
To see the entire string,
we can print it to the standard output
(standardOutput),
to an output file
(outputFile),
or to the Celestia console
(console).
In the latter case,
we must set the
LogSizeLogSize (parameter in celestia.cfg)
in
celestia.cfg
to at least 222.
Another recursive function is the
gcd
(greatest common divisor)
in
windowDimensions.
--[[
This function displays the tree of celestial objects whose root is the first
argument. The root is indented by level pairs of blanks. Its children are
indented by level+1 pairs, its children's children by level+2 pairs, etc.
]]
require("std")
local function tree(root, level)
assert(type(root) == "userdata" and tostring(root) == "[Object]"
and type(level) == "number" and level >= 0
and math.floor(level) == level) --level is an integer
local s = (" "):repstring.rep(level) .. root:name() .. " (" .. root:type() .. ")"
local children = root:getchildren()
if #children == 0 then --The array of children is empty.
s = s .. "\n"
else
s = s .. " has " .. #children .. " satellite"
if #children > 1 then
s = s .. "s" --plural
end
s = s .. ":\n"
for i, child in ipairs(children) do
s = s .. tree(child, level + 1)
end
end
return s
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local sol = celestia:find("Sol")
local s = tree(sol, 0)
celestia:print(s:sub(1, 2^10 - 1), 60, -1, 1, 1, -1) --upper left
wait()
end
main()
The indentation shows who belongs to whom:
Sol (star) has 42 satellites: Mercury (planet) Venus (planet) Earth (planet) has 4 satellites: Moon (moon) Hubble (spacecraft) ISS (spacecraft) Mir (spacecraft) Mars (planet) has 2 satellites: Phobos (moon) Deimos (moon) etc.
A simpler way to perform the same traversal is with standard library method
Object:familyObject:family.
It returns an
iterator
which can be called over and over by a generic
for
loop,
with each call returning a different celestial object.
When the iterator returns
nilnil (Lua value),
the loop terminates.
The
level
tells how far the object is located down the tree;
the root is at level 0.
The output is the same as in the previous example.
--[[
Traverse (in "preorder") the tree of celestial objects whose root is Sol.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local s = ""
for level, object in celestia:find("Sol"):family() do
s = s .. (" "):rep(level) .. object:name()
.. " (" .. object:type() .. ")"
local n = #object:getchildren()
if n > 0 then
s = s .. " has " .. n .. " satellite"
if n > 1 then
s = s .. "s" --plural
end
s = s .. ":"
end
s = s .. "\n"
end
celestia:print(s:sub(1, 2^10 - 1), 60, -1, 1, 1, -1) --upper left
wait()
end
main()
Write a recursive function named
numberOfAncestors
that returns an object’s number of ancestors.
For example,
the Moon has three ancestors:
the Earth, Sun,
and Solar System Barycenter.
The function should begin by
asserting
that its argument is a
"userdata"
and an
[Object].
Then it should get the parent of the object,
using the “info table” in
infoTable.
local info = object:getinfo()
local parent = info.parent
If the parent is
nil,
the object has no ancestors and we can return zero.
If the parent is not
nil,
the object’s number of ancestors is the parent’s
number of ancestors, plus 1.
[For
Space CadetsSpace Cadet
only.]
Read the method
Object:pathname
in the standard library in
stdCelx.
Then let
numberOfAncestors
be a method of class
Object.
Add
numberOfAncestors
to the
metatablemetatable (Lua)
that is shared by every celestial object of class
Object.
The keys of a table do not have to be integral, positive, or even numeric.
For example,
the keys of the following table are the strings
"Aries",
"Taurus",
"Gemini",
etc.
A
key/value pair
whose key is a string is called a
fieldfield (of table).
The first three fields are created without writing anything around the key.
We can do this only if the key is a string that is a valid Lua variable name.
The last three fields have keys that are not valid names.
They are disqualified by the embedded blank in
"Ursa Major",
the leading digit in
"4nax",
and the special character
ö
in
"Boötes".
(The
diaeresis
may not be portable,
and I don’t want to risk it.
See
specialCharacters
for special characters.)
If the key is not a valid name,
it must be surrounded with
[square brackets].
If the key is a string, it must also be surrounded with
"double quotes".
A value can be accessed with a
dot. (field operator)
if its key is a valid Lua variable name;
see
epithet.Aries.
The value must be accessed with square brackets if the key is not a valid
name; see
epithet["Ursa Major"].
We can loop through the fields of a table with the Lua function
pairspairs (Lua function).
Warning:
the loop is guaranteed to visit every field in the table,
but the order in which they will be visited is impossible to predict.
--[[
Loop through a table of fields (i.e., a table that is not an array)
with the function pairs.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local epithet = {
Aries = "Ram", --"Aries" is the key, "Ram" is the value
Taurus = "Bull",
Gemini = "Twins",
["Ursa Major"] = "Great Bear", --"Ursa Major" is the key
["4nax"] = "Furnace",
["Bo" .. std.char.ouml .. "tes"] = "Herdsman"
}
local s = "Aries is the " .. epithet.Aries .. ".\n"
.. "Ursa Major is the " .. epithet["Ursa Major"] .. ".\n\n"
for key, value in pairs(epithet) do
s = s .. key .. " the " .. value .. "\n"
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
Aries is the Ram.
Ursa Major is the Great Bear.
Taurus the Bull
Ursa Major the Great Bear
Aries the Ram
4nax the Furnace
Boötes the Herdsman
Gemini the Twins
Each celestial object has a read-only table of fields called the
info table.
The table’s set of keys depends on the type of the object:
a planet has an
albedo,
a star has a
stellarClass,
and a galaxy has a
hubbleType.
The corresponding values come from the database and catalogs files
listed in the configuration file
celestia.cfgcelestia.cfg (configuration file).
The values are of many data types:
name
is a
string,
hasRings
is a
boolean,
and
parent
is a celestial object or
nil.
A value that is neither a string nor a number must be explicitly converted
tostring
before it can be
concatenatedconcatenation
to another string with the
.... (concatenation operator)
operator.
Just to be safe, we will convert all of them to strings.
The
name,
type,
and
radius
fields of the info table
have the same values as the
name,
type,
and
radius
methods of class
Object.
(With one caveat.
The
radius
method is always in kilometers.
The
radius
field is in lightyears for
deep sky objectsdeep sky object,
and in kilometers for everything else.)
The
radius
field of a planet is the equatorial radius, not the polar radius.
The height fields of the info table are in kilometers.
The periods are in Earth days, even for comets.
The
atmosphereCloudSpeed
is in radians per day,
even though the
CloudSpeed
in
data/solarsys.ssc
is in degrees per day.
Temperatures are in Kelvin
(temperatureDistance),
masses are in multiples of the Earth’s mass
(miscDistance),
and the lifespan endpoints are in TDB time
(tdb).
The
infinitiesinfinity
are formatted differently on each platform
(inf
on Mac and Linux,
1.#INF
on Microsoft Windows)
and are not to be taken as an endorsement of the
Steady State
theorySteady State theory (cosmology).
--[[
Display an object's info table.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local object = celestia:find("Sol/Earth")
local info = object:getinfo()
assert(type(info) == "table")
local s = ""
for key, value in pairs(info) do
s = s .. key .. " "
if type(value) == "userdata" and tostring(value) == "[Object]"
then
s = s .. value:name()
else
s = s .. tostring(value)
end
s = s .. "\n"
end
celestia:print(s, 60, -1, 1, 1, -1) --upper left corner of window
wait()
end
main()
atmosphereCloudSpeed 1.1344640254974
type planet
albedo 0.30000001192093
lifespanEnd inf
parent Sol
hasRings false
atmosphereCloudHeight 7
atmosphereHeight 60
orbitPeriod 365.25
mass 0
name Earth
lifespanStart -inf
infoURL
oblateness 0
rotationPeriod 0.99726955833333
radius 6378.1401367188
The info table uses double variables
(doubleArithmetic)
for four of the fields:
lifespanStart
and
lifespanEnd,
orbitPeriod
and
rotationPeriod.
Print them in their full 15-digit glory.
The other numeric fields are merely float variables
and should be printed with only 6 significant digits.
Print the fields in
alphabetical ordersorting
of their keys.
I wish we could pass the table to the Lua function
table.sorttable.sort,
but this function accepts only an array,
not an arbitrary table of fields.
The workaround is to copy the keys into an array,
and then sort the array.
table.insert(keys, key)
end
table.sort(keys)
We can now loop through the keys in alphabetical order.
for i, key in ipairsipairs (Lua function)(keys) do
value = info[key]
s = s .. key .. " "
if type(value) == "userdata" and tostring(value) == "[Object]"
then --etc.
albedo 0.3
atmosphereCloudHeight 7
atmosphereCloudSpeed 1.13446
atmosphereHeight 60
hasRings false
etc.
Display the info table for the star
"Betelgeuse"Betelgeuse (star),
the globular cluster
"M 13"M13 (globular cluster)
in
HerculesHercules
(one space after the M),
the
Andromeda
GalaxyAndromeda Galaxy (M31)
"M 31"M31 (Andromeda Galaxy),
and the city
"Washington D.C."Washington, DC
(no comma, one space, two periods).
Lua, Celx, and the Celx Standard Library have many tables of fields. Print some of them.
local t = celestia:getrenderflags() --values are booleans local t = celestia:getlabelflags() local t = celestia:getorbitflags() local t = celestia:getoverlayelements() local t = celestia:getobserver():getlocationflags() local t = celestia:tdbtoutc(celestia:gettime()) --values are numbers local t = celestia:fromjulianday(celestia:gettime()) local t = os.date("*t") --must first call celestia:requestsystemaccess() local t = _G --values are all the global variables local t = getmetatable(celestia) --values are methods local t = package.loaded --values are tables local t = std.dayName --values are strings local t = std.monthName local t = std.zodiac local t = std.char --values are special characters local t = std.constellations --values are arrays of strings
One inconsistency.
The info table of
"Sol/Earth/Washington D.C."
lists the Earth as its parent,
but the Earth’s
getchildren
method
(tableOfObjects)
does not list Washington.
To get the cities and other surface features of a celestial object,
use the
iterator
returned by
Object:locationsObject:locations.
The nomenclature is surprisingly Latinate: the Earth’s continents are terræ and its oceans are maria. We’re lucky that Washington isn’t an urbis.
NORTH AMERICA (terra) 5000 km NORTH ATLANTIC OCEAN (mare) 6400 km Washington D.C. (city) 1 km etc.
This section illustrates a few applications of the info table.
We will read the
albedo
and
parent
fields of a planet,
and the
bolometricMagnitude
and
temperature
fields of a star.
The
Stefan–Boltzmann
Law
says that when a body’s temperature is doubled,
the outflow of energy through its surface is multiplied by a factor of 16.
The exact statement of the law is
S = σT4
where
T
is the temperature in Kelvin,
S
is the outward
flux
in
wattswatt
per
square meter,
and
σσ (Stefan-Boltzmann constant)
is the
Stefan–Boltzmann
constantStefan-Boltzmann constant
with a value of
5.670372 · 10–8
Wm–2
K–4.
For big objects,
we will work with square kilometers instead of square meters.
The
σ,
by the way,
is the Greek lowercase letter sigma.
It’s in the Celx standard library as
std.char.sigma.
The temperature of a star can be read by a Celx program from the
temperature
field of the star’s info table
(infoTable).
The temperature of a non-luminous body—a planet,
moon, asteroid, comet, spacecraft, or exoplanet—is not available
to the program,
but is displayed on the screen when Celestia is in
verbose mode.
On Mac,
Celestia →
Preferences →
General →
Info Display: Verbose
On Windows,
Render →
View Options… →
Information Text: Verbose
Then select the body as in
keystroke.
The non-luminous temperature is an estimate derived from the following calculation, which we will reproduce in Celx. Temperatures are in Kelvin; distances are in kilometers; areas are in square kilometers.
Let R be the radius of the Sun (or nearest star). Then the surface area of the Sun is 4πR2 Let T be the surface temperature of the Sun. Then the total outward flux coming through the surface is (4πR2)(σT4) Let d be the distance from the Sun to the planet (or other non-luminous body). Picture the planet on the surface of a sphere centered at the Sun. The radius of this sphere is d and its area is 4πd2 The flux per square kilometer through the surface of the sphere is therefore (4πR2)(σT4) 4πd2 = R2σT4 d2 Let r be the radius of the planet. The area of the disk that the planet presents to the Sun is πr2 The total flux received by the planet is therefore R2σT4 d2 πr2 But a certain fraction of this flux is reflected back into space. This fraction is called the albedo and denoted by a. The fraction absorbed by the planet is 1 − a, so the total flux absorbed is only R2σT4 d2 πr2(1 − a) Meanwhile, the planet is also radiating energy. The surface area of the planet is 4πr2 Let t be the temperature of the planet. The outgoing total flux through the surface of the planet is (4πr2)(σt4) If the temperature of the planet is constant, the incoming and outgoing flux must be equal: R2σT4 d2 πr2(1 − a) = (4πr2)(σt4) We can solve this equation for t4, t4 = R2T4(1 − a) 4d2 and then for t. t = T(1 − a).25(R/2d).5
--the non-luminous celestial object whose temperature is sought local object = celestia:find("Sol/Mars") celestia:select(object) --display temperature in verbose mode --Find the object's star. assert(object:type() ~= "star") local star = object repeat star = star:getinfo().parent assert(star ~= nil) until star:type() == "star" local distance = star:getposition():distanceto(object:getposition()) assert(distance > 0) --Don't divide by zero. local temperature = star:getinfo().temperature * (1 - object:getinfo().albedo)^.25 * (star:radius() / (2 * distance))^.5 local s = string.format("%.15g K", temperature) 226.707505428186 KDoes the above code agree with Celestia’s estimates? Get the real temperatures of the planets from Wikipedia and observe that Celestia’s estimates are correct for MarsMars, temperature of and PlutoPluto, temperature of. But why are they too low for the EarthEarth, temperature of and way too low for VenusVenus, temperature of?
Celestia tries to get the
radiusradius of star
of a star from the file
data/charm2.stccharm2.stc (data file).
If the star is not found,
it estimates the radius from the star’s
luminosityluminosity of star
and temperature.
We will reproduce the estimate in Celx.
As above,
temperatures are in Kelvin,
distances are in kilometers,
and areas are in square kilometers.
For reference purposes, we begin by computing the luminosity of the Sun. Let R be the radius of the Sun. Then its surface area is 4πR2 Let T be the surface temperature of the Sun. Then the total outward flux coming through the surface is (4πR2)(σT4)
This total flux is called the Sun’s bolometric magnitudebolometric magnitude. Unlike plain old magnitude, itmagnitude, bolometric includes the Sun’s power output in ultraviolet, visible, infrared, radio, and all other wavelengths.
The value of the bolometric magnitude gets smaller as the star’s power output increases. For example, a star with 100 times the output of the Sun would have a bolometric magnitude that is 5 less than the Sun’s. Let’s break it down into smaller intervals. A star with 1001/5 ≈ 2.51188643150958 times the output of the Sun has a bolometric magnitude that is 1 less than the Sun’s. And a star with 1002/5 ≈ 6.30957344480193 times the output of the Sun has a bolometric magnitude that is 2 less than the Sun’s. See loopDatabase for the convention of “five magnitudes span a factor of 100.” With the star’s bolometric magnitude, we can compute how many times brighter it is than the Sun. Let’s call this factor f. The total output of the star is therefore (4πR2)(σT4)f Let r be the radius of the star. Then its surface area is 4πr2 Let t be the surface temperature of the star. Then its total output is (4πr2)(σt4) But we determined that this quantity is equal to f times the Sun’s output: (4πr2)(σt4) = (4πR2)(σT4)f Solving for r yields the radius of the star. r = T2 t2 R f
Let’s pick a star that is not in
data/charm2.stc,
such as
ThubanThuban (star)
or
Castor.
Celestia displays Thuban’s radius as 4,110,000 kilometers, because it rounds it to three significant digits.
Radius = 4105400.09838207 kilometers
A note for readers of the C++ member function
Star::getRadius
in
version/src/celengine/star.cpp.
The cryptic
LN_MAGLN_MAG (macro)
is
The above calculation gives us the following radius for
"Sirius A"Sirius (star),
in good agreement with the
radius
field of that star’s info table.
Radius = 1337211.70699272 kilometers
Butbug in Celestia
the radius of Sirius A is supposed to be
1,180,000
kilometers because of the following entry in
data/charm2.stc.
What went wrong? Hint:
--[[ "Sirius" is the barycenter of the Sirius system; "Sirius A" and "Sirius B" are the stars. The radius of a stellar barycenter is supposed to be .001 kilometers. ]] local barycenter = celestia:find("Sirius") local info = barycenter:getinfo() local s = string.format( "name %s\n" .. "catalogNumber %u\n" .. "stellarClass %s\n" .. "radius %.15g kilometers", info.name, info.catalogNumber, info.stellarClass, info.radius) name Sirius catalogNumber 32349 stellarClass Bary radius 1180000 kilometers
The renderflags are a table of read/write
boolean
values that
determine what features of the Universe are rendered.
These include celestial objects such as planets and galaxies,
reference lines such as grids and orbits,
and rendering styles such as
smoothlines
and
automag.
See
Object:setorbitvisibilityObject:setorbitvisibility
for the
complicated interactionorbit visibility
between the renderflags and the
orbitflags.
Let’s turn the flags off,
sit in the dark for a few seconds,
and restore them on exit with
celestia_cleanup_callbackcelestia_cleanup_callback (function)
(callback).
See
hertzsprungrussell
for an example where we actually do turn off all the renderflags.
The callback function uses the local variable
save,
so it would make no sense for the function to outlive this variable.
But a callback has to be nonlocal.
--[[
Set the renderflags to sane values and print them.
Then turn them all off, wait in the dark for a few seconds,
and restore them to their sane values.
]]
require("std")
--Variables used by more than one function.
local save = {} --Create an empty table.
local duration = 10 --seconds of real time
local function printFlags()
local s = ""
for key, value in pairs(celestia:getrenderflags()) do
s = s .. key .. " " .. tostring(value) .. "\n"
end
return s
end
function celestia_cleanup_callback() --can't be local
--Restore the original flags.
celestia:setrenderflags(save)
celestia:print("Back to sane renderflags:\n" .. printFlags(),
duration, -1, 1, 1, -1)
wait(duration)
celestia_cleanup_callback = nil --Destroy this function.
end
local function main()
local observer = celestia:sane() --Changes the renderflags.
observer:setposition(std.position)
--Save the flags.
local flags = celestia:getrenderflags()
for key, value in pairs(flags) do
save[key] = value
end
celestia:print("Renderflags set by Celestia:sane:\n" .. printFlags(),
duration, -1, 1, 1, -1)
wait(duration)
--Turn off all the flags. Sit in darkness for duration seconds.
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setrenderflags(flags)
celestia:print("Renderflags off:\n" .. printFlags(),
duration, -1, 1, 1, -1)
wait(duration)
end
main()
Here are the values set by
Celestia:saneCelestia:sane,
alphabetized for your convenience.
Save and restore the
label flags
too,
with
Celestia:getlabelflagsCelestia:getlabelflags
and
Celestia:setlabelflagsCelestia:setlabelflags.
Save and restore the
orbitflags
with
Celestia:getorbitflagsCelestia:getorbitflags
and
Celestia:setorbitflagsCelestia:setorbitflags.
What about numeric values
such as the ambient light level or the galaxy light gain?
See the method
Celestia:sane
in
stdCelx
for the complete list of savable properties.
Here are two ways to do the same thing. Which is easier?
--Turn on ecliptic and eclipticgrid, --turn off cloudmaps and cloudshadows. local flags = celestia:getrenderflags() flags.ecliptic = true flags.eclipticgrid = true flags.cloudmaps = false flags.cloudshadows = false celestia:setrenderflags(flags) --Turn on ecliptic and eclipticgrid, --turn off cloudmaps and cloudshadows. celestia:showCelestia:show("ecliptic", "eclipticgrid")
celestia:hideCelestia:hide("cloudmaps", "cloudshadows")
The special value
nilnil (Lua value)
can never be the value—or the key—of any field in a table.
To test if a key exists,
it therefore suffices to check if the corresponding value is
nil.
The following example loops through all the ancestors of a celestial object.
The loop will keep going as long as there is a key named
parent
in the info table of the current object.
See
Object:pathname.
--[[
Loop through all the ancestors of an object. Print them one per line.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local object = celestia:find("Sol/Earth/Moon/Tycho")
local s = object:name() .. " and its ancestors are\n"
local i = 0
repeat
i = i + 1
local info = object:getinfo()
local type = object:type()
if type == "location" then
type = type .. ", " .. info.featureType
elseif type == "star" then
type = type .. ", " .. info.stellarClass
end
s = s .. string.format("%d %s (%s)\n", i, info.name, type)
object = info.parent
until object == nil
local duration = 60
celestia:print(s, duration, -1, 0, 1, 0)
wait(duration)
end
main()
Tycho and its ancestors are
1 Tycho (location, crater)
2 Moon (moon)
3 Earth (planet)
4 Sol (star, G2V)
5 Solar System Barycenter (star, Bary)
Celestia comes with a database of a hundred thousand stars,
including miscellaneous objects such as
neutron stars
and the
barycenters
of stellar systems.
We can loop through the database with the
iterator
returned by
Celestia:starsCelestia:stars.
The
ArabicArabic language
word for “head” is
رأس
(ra’s).
Let’s find every star that’s a head.
The following
[Rr]
is a
wildcardwildcard (in pattern)
that looks for an upper or lowercase letter R.
A wildcard is a simple example of a
patternpattern (Lua).
--[[
List the stars that are heads ("ras" in Arabic).
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
wait() --Render a view for the user to watch during the long loop.
local s = ""
--The method Celestia:stars returns an iterator.
assert(type(celestia.stars) == "function"
and type(celestia:stars()) == "function")
for star in celestia:stars() do
assert(type(star) == "userdata"
and tostring(star) == "[Object]"
and star:type() == "star")
--If it's really a star,
--and not the barycenter of a stellar system,
if star:getinfo().stellarClass ~= "Bary" then
local name = star:name()
if name:findstring.find("[Rr]as") then --"head (of)" in Arabic
s = s .. name .. "\n"
end
end
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
Comments are in parentheses.
Rasalgethi (α Herculis, Head of the Kneeler) Rastaban (β Draconis, Head of the Serpent [cf. Thuban]) Ras Elased Australis (ε Leonis, Head of the Lion, south) Rasalas (μ Leonis, Head of the Lion) Rasalhague (α Ophiuchi, Head of the Serpent)
The Arabic word for “tail” is
ذنب
(danb).
Let’s find the tails.
The wildcard
%a%a (in pattern)
looks for any letter,
upper or lowercase.
The expression
%a** (in pattern)
looks for any string of zero or more consecutive letters.
This ensures that the D, N, and B will belong to the same word,
with no whitespace between them.
We missed
Deneb KaitosDeneb Kaitos (star)
(β Ceti,
the tail of
CetusCetus)
because its
name
method returns
"Diphda"Diphda (star).
To examine all the names of a star,
see
inputFile.
Find the stars whose names contain “of the”. if name:find(" [AaEe]l") then --"of the" in Arabic We required a space before the letters to avoid finding words such as Camelopardalis or Velorum. But the space caused us to miss many celebrated stars: ZubenelgenubiZubenelgenubi (star) (α Libræ, the Southern Claw), FomalhautFomalhaut (star) (α Piscis Austrini, the Mouth of the Whale), and BetelgeuseBetelgeuse (star) (α Orionis, the Hand of Orion).
Na'ir al Saif (ι Orionis, Bright One of the Sword) Minhar al Shuja (σ Hydræ, Nose of the Hydra) Ras Elased Australis (ε Leonis, Head of the Lion, south) Al Dhanab al Dulfim (ε Delphini, the Tail of the Dolphin) Deneb el Okab (ζ Aquilæ, Tail of the Falcon) Deneb Algedi (δ Capricorni, the Head of the Goat) Zuben Elakribi (δ Libræ, the Claw of the Scorpion) Zuben Elakrab (γ Libræ, the Claw of the Scorpion) Fum al Samakah (β Piscium, the Mouth of the Fish)
We can get the planets of a star by calling its
getchildrenObject:getchildren
method
(tableOfObjects).
Let’s go prospecting for
exoplanetsexoplanet
with liquid
waterwater, liquid.
See
temperatureDistance
for the temperature calculation.
Why didn’t it find the Earth?
BD+20 2457/b 39.249° C BD+20 2457/c 3.072° C TYC 3304-101-1/b 35.913° C etc.
To find the
neutron starsneutron star,
look for the stars whose
stellarClass
starts with
Q.
^ (anchor in pattern)) means "starts with".
if star:getinfo().stellarClass:findstring.find("^Q") then
Are there any
black holesblack hole
(stellar class "X")?
If not,
create the following “star catalog” file named
imaginary.stcstc file, create your own
in the
data
subdirectory of the Celx directory
(celxDirectory).
Then add the filename
"data/imaginary.stc"
to the list of
StarCatalogsStarCatalogs (in celestia.cfg)
in the configuration file
celestia.cfg
and restart Celestia.
Does the black hole bathe the Earth in a rosy light?
Select
MyBlackHole and go there with the
g
keystroke
(keystroke).
Is the surface of the black hole sharp or fuzzy?
(On Mac, the console says we load an image from the file
textures/lores/astar.jpg
and I get a white, sharp hole.
On Microsoft Windows,
I sometimes get a black, fuzzy hole.)
Go in for a closer look.
List the stars within 8.75 lightyears of the Solar System Barycenter, with the distance in lightyears of each star. Do not list Sol or any barycenter.
std.position0
is a
position
object
(position)
representing the position of the Solar System Barycenter.
The difference of two positions is a
vector
object
(vectors),
an arrow from one position to the other.
The
lengthVector:length
of a vector is measured in
microlightyears
(linearDistance),
so we divide it by one million to convert it to lightyears.
Celestia knows most stellar distances to only at most 10 significant digits
(see
version/data/stars.txt),
so we format them with
%.10g.
Rigel Kentaurus (The Foot of the Centaur) is the fabled Alpha Centauri.
8.5829180150 Sirius A 4.3652143469 Rigel Kentaurus A 4.3647411792 Rigel Kentaurus B 8.2900000352 Gliese 411 4.2420000986 Proxima 5.9630000000 Barnard's Star 7.7819998624 CN Leo 8.5831586381 Sirius B 8.7280489403 BL Cet 8.7279503161 UV CetList the 10 stars closest to the Solar System Barycenter, in order of increasing distance. Do not list Sol or any barycenter.
The following
t
will be an array.
Each value in
t
will be a short array
containing the name and distance in microlightyears of a star.
We will
sortsorting
t
with the closest stars first.
In
infoTable
we saw the function
table.sorttable.sort,
which applied the operator
<
to pairs of values in the array
to determine which value of the pair should come first.
This is okay if the values are numbers or strings.
But the values in
t
are arrays,
and
<
cannot be applied to a pair of arrays.
We must therefore give
sort
a two-argument comparison function to use in place of
<.
Better yet, let the comparison function be an anonymous function.
--[[ a and b are arrays, each containing two values. a[1] and b[1] are the names of two stars; a[2] and b[2] are their distances from the Solar System Barycenter. ]] table.sort(t, function(a, b) return a[2] < b[2] end)List the stars with the greatest apparent magnitudeapparent magnitude (brightnessmagnitude, apparent) as seen from Earth. A first magnitude star appears 100 times brighter than a sixth magnitude star, so five units of magnitude span a factor of 100 in brightness.
The info table does not contain a star’s apparent magnitude, but it does contain the absolute magnitudemagnitude, absolute. The absolute magnitudeabsolute magnitude of a star is the apparent magnitude it would have at a distance of 10 parsecs. Given a star’s absolute magnitude M and its distance d in parsecs, we can calculate its apparent magnitude m:
m = M + 5 · (log10 d − 1)Here’s where the logarithm comes from. For a star whose d = 10, the absolute and apparent magnitudes should be equal by definition. And they are equal, because log10 d = 1. For a star 10 times more distant but otherwise identical, the light we receive is 100 times fainter because of the inverse-square law. But this is the same factor of 100 in brightness that was spanned by 5 units of magnitude. Thus the apparent magnitude of the distant star should be 5 greater than that of the original star. And it is 5 greater, because when d gets 10 times bigger, the expression log10 d increases by 1. This causes the expression 5 · (log10 d − 1) to increase by 5.
The absolute magnitudes of most stars are known to Celestia
to only at most three significant digits
(see
version/data/stars.txt),
so we print only a few digits.
Warning:
In Lua 5.2,
the old function
math.log10math.log10.
is no longer present.
We would call
math.logmath.log
instead,
with a second argument of 10.
But the
math.log
in the Lua 5.1 in Celestia 1.6.1
accepts only one argument,
so for the time being we will continue to call the obsolete
math.log10.
Sort the stars in order of apparent magnitude as seen from earth, brightest stars first. Exclude Sol and the barycenters. Then list the first ten. You should see the table that appears in every astronomy textbook:
-1.4299 Sirius A -0.6162 Canopus -0.0474 Arcturus 0.0102 Rigel Kentaurus A 0.0281 Vega 0.0601 Capella A 0.0801 Capella B 0.1829 Rigel 0.3801 Procyon A 0.4501 BetelgeuseList the 10 brightest stars as seen from Alpha Centauri. Exclude Alpha Centauri A and B and the barycenters.
List the 10 stars of the greatest angular diameter as seen from the Solar System Barycenter. Print the name and diameter in milliarcseconds of each star. AntaresAntares (star) and Betelgeuse should be near the top of the list. Be sure to use the same unit of measurement (kilometers or microlightyears) for both the radius and the distance of each star.
Celestia believes that all the stars of a given stellar class share the same temperature. List the name and Kelvin temperature of each stellar type, one per line, in order of decreasing temperature.
--Create a table whose keys are stellar types and whose values are --Kelvin temperatures. local t = {} for star in celestia:stars() do local info = star:getinfo() if info.stellarClass ~= "Bary" then t[info.stellarClass] = info.temperature end end wait() --Copy the table into an array so we can sort it. local array = {} for key, value in pairs(t) do table.insert(array, {key, value}) end wait() --[[ Sort in order of decreasing temperature: Oh Be A Fine Girl/Guy, Kiss Me. If temperatures are equal, sort in alphabetical order. ]] table.sort(array, function(a, b) if a[2] ~= b[2] then --a[2] and b[2] are temperatures. return a[2] > b[2] end return a[1] < b[1] --a[1] and b[1] are names. end) local s = "" for i, value in ipairs(array) do s = s .. string.format("%3d %7.0f %s\n", i, value[2], value[1]) endType Q is a neutron star.
1 5000000 Q 2 60000 WC6 3 50400 DA1 etc. 497 1350 T1V 498 1020 T6V 499 800 T8VThe Gould BeltGould Belt (of stars) is a disk or ring of young, hot stars of spectral types O and B. Since we happen to be near the middle of the disk, it looks like a belt of stars along a great circlegreat circle around the sky. The plane of the belt is tilted 20° from the galactic planegalactic plane, crossing it at galactic longitude ℓ = 102° (in Vela) and ℓ = 282° (in Cephus). The belt is above (i.e., north of) the Milky Way in CentaurusCentaurus, LupusLupus (constellation), and ScorpiusScorpius, and below the Milky Way in PerseusPerseus, OrionOrion, and Canis MajorCanis Major.
Let’s mark the OB stars whose apparent magnitude is brighter than 4.5. Then pan around the sky manually, keeping the galactic plane level in the middle of the window. Compare the number of marked stars above and below the plane at each longitude. Experiment with different thresholds of magnitude.
celestia:hide("ecliptic", "grid") celestia:show("boundaries", "galacticgrid") --Mark the conspicuous stars of the Gould Belt. for star in celestia:stars() do local info = star:getinfo() if info.stellarClass:find("^[BO]") then local vector = star:getposition() - std.position0 local microlightyears = vector:length() local lightyears = microlightyears / 1000000 local parsecs = lightyears / std.lyPerPc local apparentMagnitude = info.absoluteMagnitude + 5 * (math.log10(parsecs) - 1) if apparentMagnitude < 4.5 then star:mark("green", "diamond", 10, .9, info.stellarClass) end end end
Every star and barycenter has an integer ID number in the database.
The numbers start at zero
and go up to one less than the number returned by the method
Celestia:getstarcountCelestia:getstarcount.
The ID number is not the star’s number in any of the three
catalog
(Hipparcos,
Henry
Draper,
or
Smithsonian
Astrophysical Observatory).
Celestia:getstar(id)
assert(type(star) == "userdata"
and tostring(star) == "[Object]"
and star:type() == "star")
if star:getinfo().stellarClass ~= "Bary" then
--etc.
end
Why would we want to loop with
Celestia:getstarcount
and a numeric
for
loop
rather than with
Celestia:stars
and a generic
for
loop?
Celestia comes with a database of deep sky objectsdeep sky object (DSOsDSO (deep sky object)). It contains eleven thousand galaxiesgalaxy, 150 globular clustersglobular cluster belonging to the Milky WayMilky Way, orbited by globulars, no open clustersopen cluster, and no nebulænebula. The database has its own trio of methods:
| stars | DSOs | |
|---|---|---|
| returns an iterator | Celestia:stars |
Celestia:dsos |
| returns a number | Celestia:getstarcount |
Celestia:getdsocount |
| returns an object | Celestia:getstar |
Celestia:getdso |
Let’s print the average radius in lightyears
of the
spiral,
elliptical,
and
irregular
galaxies.
The
hubbleTypehubbleType (of galaxy)
of a galaxy is a string starting with
S,
E,
or
I.
The method
string.substring.sub
returns the first character of the string.
The irregulars are much smaller than the other types.
Type # Radius Elliptical 1725 37523.0 Spiral 8548 41797.4 Irregular 664 18839.0
What percentage of the
spirals
are
barred
(Hubble types
"SBa",
"SBb",
"SBc")?
Are the irregulars closer to their neighbors than the other two types?
Is there a tendency for two neighboring spirals to spin in opposite directions?
The last question will be answered in
galacticCoordinates.
This section uses Celestia’s database of stars to construct the Hertzsprung-Russell diagram, which plots each star as a point in a two-dimensional space. The origin is in the lower right corner. The horizontal axis is the star’s temperature, increasing from right to left. The vertical axis is the star’s luminosity, increasing from bottom to top. The majority of stars lie along a diagonal line, called the main sequencemain sequence (of stars), from the lower right (cool and dim) to the upper left (hot and bright). An arm of giant starsgiant star extends to the upper right (cool and bright, hence very big).
Values in the diagram are plotted logarithmicallylogarithm: when we double the temperature, we always move to the left by the same distance. Thus the horizontal distance from 3,000 to 6,000 Kelvin is equal to the distance from 6,000 to 12,000 Kelvin.
If the star’s temperature is in the range
10self.logMinTemp
= 2,500 Kelvin
to
10self.logMaxTemp
= 50,000 Kelvin
inclusive, then the
log10
of its temperature will be in the range
self.logMinTemp
to
self.logMaxTemp
inclusive.
The size of this range is
self.rangeTemp.
The expression
(math.log10(info.temperature) - self.logMinTemp) / self.rangeTemp
will be a fraction in the range 0 to 1 inclusive.
And the expression
-self.width * (math.log10(info.temperature) - self.logMinTemp)
/ self.rangeTemp
will be a distance in pixels in the range 0
to negative the width of the window,
inclusive.
(We want negative because the origin is in the lower right.
A point to the left of the origin will have a negative
x
coördinate.)
Luminosity is plotted similarly.
Warning:
the function
math.log10
is no longer present in Lua 5.2.
The array
self.a
contains more than one hundred thousand values.
Each value
is an array of two numbers
giving a star’s horizontal and vertical position in pixels
measured from an origin at the lower right corner of the Celestia window.
Depending on the speed of your machine,
it might take several seconds to create
self.a.
This is a problem because a Celx program must call the
waitwait
function
(wait)
at least once every five seconds,
and a call to
wait
inside a Lua hook never returns.
Our solution is to increase the five-second limit by calling
Celestia:settimesliceCelestia:settimeslice.
When the entire database has been read into
self.a,
the
tick
hook wipes itself out by saying
self.tick = nil.
--[[
This file is luahook.celx.
Plot the Hertzsprung-Russell diagram, featuring the main sequence of stars.
]]
celestia:setluahook {
width = nil, --of window, in pixels
height = nil,
a = {}, --array of stars, not including barycenters
--logs of surface temperature in Kelvin
logMinTemp = math.log10(2.5e3), --coolest, right edge of window
logMaxTemp = math.log10(5e4), --hottest, left edge of window
rangeTemp = nil,
--logs of luminosity in multiples of Sol's
logMinLum = math.log10(3e-4), --dimmest, bottom edge of window
logMaxLum = math.log10(2e4), --brightest top edge of window
rangeLum = nil,
--Return the x, y coordinates in pixels of the given point,
--measured from an origin in the lower right corner of the window.
coordinates = function(self, temperature, luminosity)
return -self.width
* (math.log10(temperature) - self.logMinTemp)
/ self.rangeTemp,
self.height
* (math.log10(luminosity) - self.logMinLum)
/ self.rangeLum
end,
tick = function(self)
self.tick = nil --No need to call this hook more than once.
require("std")
self.rangeTemp = self.logMaxTemp - self.logMinTemp
self.rangeLum = self.logMaxLum - self.logMinLum
self.width, self.height = celestia:getscreendimension()
celestia:settimeslice(10) --Ask for even more seconds if needed.
for star in celestia:stars() do
local info = star:getinfo()
if info.stellarClass ~= "Bary" then
table.insert(self.a, {self:coordinates(
info.temperature, info.luminosity)})
end
end
celestia:settimeslice(5) --Restore the default.
end,
renderoverlay = function(self)
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
--dimensions of the Celestia window, in pixels
local width, height = celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height) --left, right, bottom, top
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
--The default origin (0, 0) is at the lower left corner of the
--window. Move the origin to the lower right corner.
gl.Translate(width, 0)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING) --Make text and graphics self-luminous.
gl.Disable(gl.TEXTURE_2D) --disabled for graphics
gl.Color(1, 1, 1, 1) --red, green, blue, alpha
gl.Begin(gl.POINTS) --isolated points
for i, value in ipairs(self.a) do
gl.Vertex(value[1], value[2])
end
gl.End()
--Yellow square around Sol.
gl.Color(1, 1, 0, 1)
local size = 2
local info = celestia:find("Sol"):getinfo()
local solX, solY =
self:coordinates(info.temperature, info.luminosity)
gl.Begin(gl.LINE_LOOP) --connected lines
gl.Vertex(solX + size, solY - size) --lower right corner
gl.Vertex(solX + size, solY + size) --upper right
gl.Vertex(solX - size, solY + size) --upper left
gl.Vertex(solX - size, solY - size) --lower left
gl.End()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
end
}
--[[
Provide a black background for the OpenGL graphics. Turn off all the flags.
]]
require("std")
local function main()
celestia:sane()
local flags = celestia:getrenderflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setrenderflags(flags)
flags = celestia:getlabelflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setlabelflags(flags)
flags = celestia:getoverlayelements()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setoverlayelements(flags)
--No need to face away from the Sun: the Sun is not being rendered.
wait()
end
main()
Is the yellow box around Sol missing one of its corners?
If so,
fix it by rounding
solX
and
solY
to the closest number that is .5 greater than an integer.
Where is the
red giant
BetelgeuseBetelgeuse (star)
in the diagram?
What about the
white dwarf
"Sirius B"Sirius B (star)
(one blank, uppercase B)?
What would happen to the diagonal line of the main sequence if the scales of the axes were changed from logarithmic to linear?
Let the
main
function loop through the three tables of flags with a
for
loop.
We can think of the
celestiacelestia (object)
object as being a table of functions.
Each function receives the
celestia
object as its first or only argument.
The stars are grouped into vertical lines because Celestia assigns the same temperature to every star of a stellar class. For example, every star of the Sun’s class G2VG2V (spectral type) has the Sun’s temperature of 5860 Kelvin. Blur out the lines by adding a small random value (positive or negative) to each star’s temperature.
Colorcolor, of star
the stars by their temperature.
The C++ array
StarColors_Blackbody_2deg_D65
in
version/src/celengine/starcolors.cpp
gives us the rgb color
corresponding to a given Kelvin temperature.
Create a Celx array containing the same information.
The array should be a field of the Lua hook table,
initialized when we
require("std").
Get a star’s temperature in Kelvin from the star’s info table
(infoTable)
and look up the corresponding rgb value in the array.
See the member function
ColorTemperatureTable::lookupColor
in
version/src/celengine/starcolors.h.
We have seen five functions that return an iterator:
ipairs
(arrayOfStrings),
pairs
(tableOfFields),
Object:locations
(infoTable),
Celestia:stars
(loopDatabase),
and
Celestia:dsos
(loopDatabase).
Now let’s write our own function that returns an iterator.
The
signs
in the following program is clearly a function.
What is surprising is that
signs()—the
return value of
signs—is
also a function.
Since the latter function has no name we refer to it as an
anonymous
functionanonymous function.
The anonymous function is called over and over by the
generic
for
loop.
Each call returns the next value in a series of values,
or
nilnil (Lua value)
when the series is exhausted.
The
nil
breaks us out of the loop.
A function used in this way is referred to as an
iterator.
The iterator is created inside the function
signs.
This allows the iterator mention the local variable(s)
of
signs,
in this case
i.
Our simple program calls
signs
only twice:
in the assertion and at the start of the
for
loop.
A more complicated program might call
signs
many times.
Since
signs
creates and returns a new iterator each time it is called,
we say that
signs
is a
factory functionfactory function.
A call to the factory creates more than just another copy of the iterator.
It also creates another copy of the local variable(s),
in this case i,
for use by the iterator.
Since each iterator has its own copy of
i,
we could have more than one iterator traversing the array at the same time.
--[[
Create an iterator for looping through a table.
]]
require("std")
local signsTable = {
"Aries",
"Taurus",
"Gemini",
"Cancer",
"Leo",
"Virgo"
}
local function signs()
local i = 0 --the first key, minus 1
--Create an iterator and return it.
--The iterator is an anonymous function.
return function()
i = i + 1
if i <= #signsTable then
--The iterator returns a pair of values.
return i, signsTable[i]
end
end
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local s = ""
assert(type(signs) == "function" and type(signs()) == "function")
--i and sign are the two values returned by each call to the iterator.
for i, sign in signs() do
s = s .. i .. " " .. sign .. "\n"
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
1 Aries
2 Taurus
3 Gemini
4 Cancer
5 Leo
6 Virgo
Read the two factories in the standard library:
the function
std.xyz
(simple; see observerSetposition)
and the method
Object:family
(complicated; see
Recursion).
Write a factory that returns an iterator that returns all the names of a star or deep-sky object, one by one. See inputFile.
local star = celestia:find("Betelgeuse") local s = "" for name in names(star) do s = s .. name .. "\n" end
For
Space CadetsSpace Cadet
only:
let the factory be a method of class
Object.
Write a factory that returns an iterator that returns all the galaxies
except a given galaxy,
in order of increasing distance from the given galaxy.
You’ll have to wait until we do
Object:getposition
in
objectGetposition.
Write a factory that returns an iterator that returns all the stars,
like
Celestia:stars,
but relieves the user of having to call
wait
every 5 seconds while the loop is in progress.
Use
Celestia:getscripttime.
Simulation timesimulation time
is the time that passes in the Celestia universe.
It can be
“get” and
“set” with
Celestia:gettime
and
settime,
and speeded up, slowed down, halted, or reversed with
Celestia:settimescale.
Simulation time is measured in Earth days.
Examples include the time fields of a celestial object’s info table
(infoTable):
rotationPeriod,
orbitPeriod,
lifespanStart,
and
lifespanEnd.
The
atmosphereCloudSpeed
is in radians per day.
Real timereal time
is the time that passes in the universe
of the user sitting in front of the Celestia application.
It cannot be set or accelerated—we just have to wait for it to pass.
The current real time is returned by
Celestia:getsystemtime
and the Lua functions
os.date
and
os.time.
Intervals of real time are measured in seconds.
For example,
Celestia:getscripttime
returns the number of seconds of real time since the
Celx script started running,
and the argument of
wait
specifies how many seconds until the script runs again.
The standard library constants
std.logo
and
std.duration
are in seconds of real time.
So are the time arguments and return value of the following functions.
wait
and
Celestia:settimesliceCelestia:print,
flash,
mmprint
Observer:goto,
gotodistance,
gotolocation,
gotolonglat,
gotosurface,
center,
centerorbit
Observer:setspeed
and
getspeed,
in microlightyears per second of real time
tick
Lua hook
(luaHookFunctions).
The current real time is returned by the method
Celestia:getsystemtimeCelestia:getsystemtime
in
UTCUTC (Coördinated Universal Time),
i.e., Greenwich Mean Time.
The return value is updated only once per second.
(The fractional part of the current second is chopped off by the
C language castcast (C language)
(int)
in the member function
astro::Date::systemDate
in
version/src/celengine/astro.cpp.)
The return value is one big number called a
Julian dateJulian date,
giving the number of days that have elapsed since noon
on Monday, January 1, 4713 B.C.
The Julian date is currently up in the two millions and climbing,
and can include a fraction.
The method
Celestia:tdbtoutcCelestia:tdbtoutc
breaks out a Julian date into a table
with six humanly readable fields:
year,
month,
day,
hour,
minute,
seconds.
The first five fields are integers.
The last field can have a fraction,
which we can chop off with
math.floor
or round with
std.round.
The month numbers range from 1 to 12 inclusive,
the hours from 0 to 23 inclusive.
The following program formats the hours, minutes, and seconds
as two-digit numbers,
with a leading zero if necessary.
The Lua function
os.dateos.date
can return the current real time in UTC or the local time zone.
It accepts the same
% formats% format (os.date)
as the C function
strftimestrftime (C function).
For example,
%z
is our zone’s number of hours and minutes ahead of UTC.
The return vaue is a humanly-readable string.
Three warnings.
(1)
The table returned by
Celestia:tdbtoutc
does not have the same field names as the tables passed to
os.timeos.time
and returned by
os.date.
(2)
The table returned by
Celestia:tdbtoutc
is in UTC,
while the table passed to
os.time
is in local time.
(3)
If your times are about 66 seconds ahead of where they should be,
you have probably called
Celestia:fromjulianday
instead of
Celestia:tdbtoutc.
See
stepThrough.
--[[
Display the current real time in UTC and the local time zone,
updated every second. Microsoft Windows doesn't have the %z format.
]]
require("std")
local function tickHandler()
local tdb = celestia:getsystemtime() --tdb is the current Julian date.
assert(type(tdb) == "number")
local utc = celestia:tdbtoutc(tdb)
assert(type(utc) == "table")
local s = string.format(
"Real Time:\n"
.. "%.15g\n"
.. "%d %.3s %d %02d:%02d:%02d UTC\n" --only first 3 characters
.. "%s\n"
.. "%s",
tdb,
utc.year, std.monthName[utc.month], utc.day,
utc.hour, utc.minute, std.round(utc.seconds),
os.date("!%Y %b %d %H:%M:%S %Z"), --exclamation point for UTC
os.date( "%Y %b %d %H:%M:%S %Z (%z)")) --no ! for local time
celestia:print(s, 1, 1, 1, -22, -2) --upper right, below simulation time
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:requestsystemaccess() --Get permission to mention os.
wait()
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Real Time:
2456316.40773362
2013 Jan 23 21:46:02 UTC
2013 Jan 23 21:46:02 UTC
2013 Jan 23 16:46:02 EST (-0500)
Verify that the simulation time runs in sync with the real time by default. Then speed up the simulation time by pressing three lowercase Ls. Observe that this has no effect on the speed of the real time.
The above program displayed the time as a string.
Let’s get one of the fields as a numeric value,
e.g., the current hour of the day.
A string returned by
os.date
can be converted to a number with the Lua function
tonumbertonumber (Lua function).
Create an array of
localizedlocalization
month names by calling
the Lua functions
os.time
and
os.date.
os.setlocale("fr_CA")
local monthName = {} --Create an empty table.
for m = 1, 12 do
local t = {year = 2000, month = m, day = 1}
table.insert(monthName, os.date("%B", os.time(t)))
end
On Macintosh and other Unixes,
we can change the environment variable
LC_ALLLC_ALL (environment variable)
directly instead of calling
os.setlocale.
Or we can change the environment variable only for Celestia:
LC_ALL=fr_CA Celestia myprog.celxThe French “February” is février on Mac, frier on Microsoft Windows. Vive la différence.
1 janvier 2 février 3 mars etc.Simulation time can be expressed in UTC or TDB. UTCUTC (Coördinated Universal Time) is the Coördinated Universal Time kept by clocks on Earth. TDBTDB (Barycentric Dynamical Time) is the Barycentric Dynamical TimeBarycentric Dynamical Time that would be kept by a clock at the barycenterbarycenter (of Solar System) (center of mass) of the Solar System. TDB is untroubled by the difference in gravitation between mountaintop and ocean floor. It is not dilated by the acceleration of the Earth in its elliptical orbit. And it certainly doesn’t care that the Earth’s rotation is slowing down. Celestia uses TDB for all its internal needs, and UTC (or the local equivalent) only for the display in the upper right corner of the window.
Let’s display the current simulation time in TDB and UTC,
updated wth every tick of the simulation
The method
Celestia:gettimeCelestia:gettime
returns the simulation time as a
Julian dateJulian date
measured in TDB.
We can convert it to UTC with
Celestia:tdbtoutcCelestia:tdbtoutc.
--[[
Display the current simulation time in UTC and TDB, updated every tick.
]]
require("std")
local function tickHandler()
local tdb = celestia:gettime() --Get the Julian date in TDB.
assert(type(tdb) == "number")
local utc = celestia:tdbtoutc(tdb)
assert(type(utc) == "table")
local s = string.format(
"Simulation time:\n"
.. "%.15g\n"
.. "%d %.3s %d %02d:%02d:%02d UTC",
tdb,
utc.year, std.monthName[utc.month], utc.day,
utc.hour, utc.minute, math.floor(utc.seconds))
celestia:print(s, 1, 1, 1, -17, -2) --upper right, below time
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Simulation time:
2456316.51097139
2013 Jan 24 00:14:41 UTC
The inverse of
Celestia:tdbtoutc
is
Celestia:utctotdbCelestia:utctotdb.
It takes six arguments
(year, month, day, hour, minute, seconds)
and boils them back down into a Julian date.
The hour, minute, and seconds default to 0,
the month and day default to 1,
and the year defaults to 0.
The fractional part of each argument except the last is ignored.
Celestia:utctotdb
provides a user-friendly way to compose the argument of
Celestia:settime;
see
settime.
Let’s watch the shadow of the Moon travel across Europe during the total solar eclipseeclipse, solar of August 11, 1999. We will go to the start of the eclipse, fast forward through it at 600 times the normal speed, and revert to the original speed when it is over.
It’s easy to go to the start of the eclipse
with
Celestia:settimeCelestia:settime,
and
speed up the time with
Celestia:settimescaleCelestia:settimescale.
But it’s harder to go back to the original
time scale
at the end of the eclipse.
We’ll use a tick handler
(tickHandler)
to detect when the current time has reached the end of the eclipse.
The tick handler will tell Celestia to stop calling the tick handler,
and will set the time scale back to 1.
To avoid unnecessary work,
we create the variable
t1
once and for all as a global
rather than re-creating it every time the
tickHandler
is called.
Our vantage point will be four Earth radii above the subsolar pointsubsolar point—the point on the Earth where the Sun is directly overhead. A full explanation of how we keep the observer suspended there is in lockFrame. For now, we will create a moving “frame of reference” whose X axis always points from the Earth to the Sun. We keep the observer positioned on this axis, looking at the Earth, and oriented so that the universal Y axis (universalFrame) is pointing upwards.
In totality we will draw a line on the surface of the Earth along the path of totality.
--[[
Fast forward through a total solar eclipse at 600 times faster than normal
speed, then revert to the original speed.
Face the Earth from a point on the Earth-Sun line, with the north pole of the
ecliptic towards the top of the window.
]]
require("std")
--variable used by tickHandler:
local t1 = celestia:utctotdb(1999, 8, 11, 13, 50, 0.0) --end of eclipse
local function tickHandler()
if celestia:gettime() >= t1 then
--Stop calling the tickHandler.
celestia:registereventhandler("tick", nil)
--Go back to the normal speed.
celestia:settimescale(1)
end
end
local function main()
local observer = celestia:sane()
celestia:hidelabel("planets") --We know that the Earth is the Earth.
--The International Space Station is a distracting dot.
local iss = celestia:find("ISS")
iss:setvisible(false)
--Field of view of 30 degrees is wide enough to see the whole Earth.
observer:setfov(math.rad(30))
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local lockFrame = celestia:newframe("lock", earth, sol)
observer:setframe(lockFrame) --Adhere the observer to the frame.
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
observer:lookat(earth:getposition(), std.yaxis)
--a few minutes before total solar eclipse begins
local t0 = celestia:utctotdb(1999, 8, 11, 8, 10, 0.0)
celestia:settime(t0)
--Start the fast-forward as soon as the "CELESTIA" logo disappears.
wait(std.logo)
--Fast forward one hour of simulation time per 6 seconds of real time.
celestia:settimescale(60 * 60 / 6)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Instead of hardcoding the angle of the field of view into the above program, derive it from the observer’s distance from the Earth. See trigonometryFun.
--observer's distance from center of Earth, in Earth radii local distance = 5 local angularRadius = math.asinmath.asin(1 / distance) --of Earth, in radians
local margin = 1 --in degrees. Two margins, at top and bottom.
observer:setfov(2 * (angularRadius + math.rad(margin)))
The fast-forward interval has an abrupt start and end. After you have read gradualStart, come back to the above program and have the Earth pick up speed gradually.
Demonstrate that the simulation time does not advance until we call
waitwait
(wait).
--[[
Demonstrate that the simulation time does not advance until we call wait.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local s0 = celestia:getscripttime() --real time in seconds
local t0 = celestia:gettime() --simulation time in days
--Noticeable delay, but not long enough to require a call to wait.
for i = 1, 2^27 do --134,217,728
end
local s = string.format(
"The loop took\n"
.. "%.15g seconds of real time\n"
.. "%.15g seconds of simulation time",
celestia:getscripttime() - s0,
(celestia:gettime() - t0) * 24 * 60 * 60)
celestia:print(s, 60)
wait()
end
main()
The loop took
1.13859009742737 seconds of real time
0 seconds of simulation time
Also demonstrate that the simulation time in Celestia is clamped to the range
two billion BC to two billion AD
(at noon on January 1 of each year),
even though the
UniverseUniverse, age of
is almost
14 billion
years
old.
Be sure to call
wait
after calling
Celestia:settime;
what happens if you don’t?
Warning: an integer greater than or equal to
231 = 2,147,483,648
must be formatted with
"%.0f";
see
integerFormatting.
The methods
Celestia:tdbtoutcCelestia:tdbtoutc
and
Celestia:utctotdbCelestia:utctotdb
know that UTC speeds up and slows down relative to TDB.
UTC passes slowly when the Earth is moving quickly
(in early January, at
perihelionperihelion (of Earth)—the
Earth’s closest approach to the Sun).
A January UTC day is therefore longer than a TDB day.
UTC passes quickly when the Earth is moving slowly
(in early July, at
aphelionaphelion (of Earth)—the
Earth’s farthest retreat
from the Sun).
A July UTC day is shorter than a TDB day.
The plus sign in the format
%+.15g
prints a leading plus or minus.
--[[
Print the average length in TDB days of a UTC day at various times of the year.
We'll print the average of the first n UTC days of each month.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
local n = 10 --average the first n days of each month
local s = ""
for month = 1, #std.monthName do
--average length of a UTC day, measured in TDB days.
local d = (celestia:utctotdb(year, month, n + 1)
- celestia:utctotdb(year, month, 1)) / n
s = s .. string.format(
"%.2s: 1 UTC day = %17.15f TDB days = 1 day",
std.monthName[month], d)
if d ~= 1 then
s = s .. string.format(" %+.15g seconds",
(d - 1) * 24 * 60 * 60)
end
s = s .. "\n"
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
The
2.81631869825105e-05
in the first line of output stands for
2.81631869825105 · 10–5
= .0000281631869825105
Thus a UTC day can be more than 10–5 seconds longer than a TDB day. And it adds up. A hundred UTC days can be 10–3 seconds longer than a hundred TDB days.
We have seen that
Celestia:tdbtoutcCelestia:tdbtoutc
and
Celestia:utctotdbCelestia:utctotdb
know that UTC is slowed down and speeded up by the Earth’s orbit.
They also know that UTC is
occasionally delayed by a
leap second.
For example,
they know that the interval between the following times is two seconds.
11:59:59 p.m. December 31, 2008 UTC
12:00:00 a.m. January 1, 2009 UTC
A parallel pair of methods,
Celestia:fromjuliandayCelestia:fromjulianday
and
Celestia:tojuliandayCelestia:tojulianday,
takes a less sophisticated view of time.
They remain rigid in their belief that every minute has 60 seconds.
They refuse to acknowledge that the Earth’s rotation is slowing down.
They reject Einsteinian time dilation.
A sure-fire way to
get the 66-second error in
tdb
is to pass the return value of
Celestia:tojulianday
to
Celestia:settime,
or the return value of
Celestia:gettime
to
Celestia:fromjulianday.
| know about time dilation and leap seconds |
don’t know about time dilation and leap seconds |
|
|---|---|---|
| convert number to table | Celestia:utctotdb |
Celestia:fromjulianday |
| convert table to number | Celestia:tdbtoutc |
Celestia:tojulianday |
The following subtractions give us the interval in days
between the times shown above.
We multiply the intervals by
60 · 60 · 24
to convert them to seconds.
The
%.4f
rounds the answer to the nearest ten-thousandth.
--[[
Demonstrate that Celestia:utctotdb knows about leap seconds, and that
Celestia::tojulianday doesn't, by printing the distance in seconds between
23:59:59 December 31, 2008
00:00:00 January 1, 2009
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local tdb0 = celestia:utctotdb(2008, 12, 31, 23, 59, 59)
local tdb1 = celestia:utctotdb(2009, 1, 1, 0, 0, 0)
local utc0 = celestia:tojulianday(2008, 12, 31, 23, 59, 59)
local utc1 = celestia:tojulianday(2009, 1, 1, 0, 0, 0)
local s = string.format(
"Distance according to utctotdb: %.4g second(s)\n"
.. "Distance according to tojulianday: %.4g second(s)",
(tdb1 - tdb0) * 60 * 60 * 24,
(utc1 - utc0) * 60 * 60 * 24)
celestia:print(s, 10)
wait()
end
main()
Distance according to utctotdb: 2 second(s)
Distance according to tojulianday: 1 second(s)
brady. In fact, he determined that the Lord began the Creation on the 23rd of October in the year 4,004 b.c. at—uh, at 9 a.m.!
drummond. That Eastern Standard Time? (Laughter) Or Rocky Mountain Time? (More laughter) It wasn’t daylight-saving time, was it? Because the Lord didn’t make the sun until the fourth day!
The simpleminded pair
Celestia:fromjuliandayCelestia:fromjulianday
and
Celestia:tojuliandayCelestia:tojulianday
still have a modest but essential rôle to play.
Precisely because of their belief in the 60-second minute,
they provide a uniform way to step through the calendar.
Celestia:tojulianday
follows two cast-iron rules,
reminiscent of the
Peano axiomsPeano axioms (of arithmetic):
Celestia:tojulianday
has to be
–4712.)
Let’s find the day of the week of the current simulation time,
even though we could easily get it from
os.timeos.time
and
os.dateos.date.
Since the first Julian day started at noon,
we pass noon of the current day to
Celestia:tojulianday.
The variable
std.dayNamestd.dayName
is an array of seven strings,
starting with
"Monday"
because the first Julian date, January 1, 4713 B.C., would have been a Monday
if our calendar went back that far.
The expression
#std.dayName
has the value 7.
The operator
%% (remainder operator)
divides
d
by 7 and gives us a
remainder
in the range 0 to 6 inclusive.
Adding 1 gives us a sum in the range 1 to 7 inclusive,
which is used as the array subscript.
--[[
Print the day of the week of the current simulation time.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
--Get permission to mention os.
celestia:requestsystemaccess()
wait()
local tdb = celestia:gettime()
local utc = celestia:tdbtoutc(tdb)
local d = celestia:tojulianday(utc.year, utc.month, utc.day, 12)
local tab = {year = utc.year, month = utc.month, day = utc.day}
local s = string.format(
"Julian date %d\n"
.. "%s %d/%d/%d\n"
.. "%s",
d, std.dayName[d % #std.dayName + 1],
utc.month, utc.day, utc.year,
os.date("%A %m/%d/%Y", os.time(tab)))
celestia:print(s, 60)
wait()
end
main()
Julian date 2456318
Friday 1/25/2013
Friday 01/25/2013
Get the
localizedlocalization
names of the weekdays from
os.time
and
os.date
as in
realTime.
Let’s step through the calendar
and find the days that had a
leap second.
We will call
Celestia:tojulianday
to combine the current year, month, and day to a single number.
This will be the initial value of the
induction
variableinduction variable (of loop)
of the loop—the variable that the loop counts with.
During each iteration,
Celestia:fromjulianday
breaks the number back down into separate values for
year, month, and day.
The distance from midnight UTC to the next midnight UTC,
tdb1 – tdb0,
is usually one day.
If the number of days is closer to
1 +
1
60 · 60 · 24
there must have been a leap second.
--[[
List the days that had a leap second.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
--The year of the current simulation time
local year = celestia:tdbtoutc(celestia:gettime()).year
local first = celestia:tojulianday(1972, 1, 1, 12)
local last = celestia:tojulianday(year, 12, 31, 12)
local s = ""
for day = first, last do
local utc0 = celestia:fromjulianday(day)
local utc1 = celestia:fromjulianday(day + 1)
local tdb0 = celestia:utctotdb(utc0.year, utc0.month, utc0.day)
local tdb1 = celestia:utctotdb(utc1.year, utc1.month, utc1.day)
if tdb1 - tdb0 > 1 + .5 / (60 * 60 * 24) then
s = s .. string.format("%d/%d/%d\n",
utc0.month, utc0.day, utc0.year)
end
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
The last leap second Celestia currently knows about was in 2008.
6/30/1972 12/31/1972 12/31/1973 etc. 12/31/1998 12/31/2005 12/31/2008
The return value of
Celestia:fromjulianday
is ahead of the return value of
Celestia:tdbtoutc
because the former
does not know that the Earth’s rotation is slowing down.
Let’s find out how far ahead it is.
Put the following code into a
tickHandler.
The 66.1846742033958 seconds is the sum of three terms:
version/src/celengine/astro.cpp
ends in 2009.dTA
in
astro.cpp.
The reasons for this offset go back to the work of
Simon Newcomb
in the Nineteenth Century.
What is the value of the difference when the Earth is at perihelionperihelion (of Earth) in January and and aphelionaphelion (of Earth) in July? What about in April and October? Was the difference any smaller 10 years ago?
4713 B.C. was chosen as the start of the JulianJulian date numbering system because it was the most recent year that was simultaneously the first year of the solar, Metonic, and indiction cycles.
The monk Dionysius ExiguusDionysius Exiguus said that JesusJesus, birth of was born in a year that was ninth in the solar cycle, first in the Metonic cycle, and third in the indiction cycle. Since he was the inventor of the Anno DominiAnno Domini numbering system, we’ll take his word for it. A thousand years later another scholar, Joseph Justus ScaligerScalinger, Joseph Justus, counted backwards from the birth of Jesus until he found a year that was first in all three cycles. He designated that year as the start of the Julian Period.
--[[
Count backwards from the birth of Jesus to the most recent year that was first
in all three cycles: solar, Metonic, and indiction. That year is where the
Julian dates begin.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
--Dionysius Exiguus said Jesus was born in a year that was 9 in the
--solar cycle, 1 in the Metonic cycle, and 3 in the indiction cycle.
local solar = 9 --28-year solar cycle
local metonic = 1 --19-year Metonic cycle (golden numbers)
local indiction = 3 --15-year induction cycle
local year = 0
while solar ~= 1 or metonic ~= 1 or indiction ~= 1 do
year = year - 1 --Go back one year.
if solar == 1 then
solar = 28
else
solar = solar - 1
end
if metonic == 1 then
metonic = 19
else
metonic = metonic - 1
end
if indiction == 1 then
indiction = 15
else
indiction = indiction - 1
end
end
--Arrive here when solar, metonic, and indiction are all 1.
local utc = celestia:fromjulianday(0)
local s = string.format(
"Year %d was the first year of all three cycles.\n"
.. "Julian date 0 is %s %d, %d %02d:%02d:%02d UTC.",
year,
std.monthName[utc.month], utc.day, utc.year,
utc.hour, utc.minute, utc.seconds)
celestia:print(s, 60)
wait()
end
main()
Year -4712 was the first year of all three cycles.
Julian date 0 is January 1, -4712 12:00:00 UTC.
An average
rotationEarth, rotation of
rotation of the Earth with respect to the Sun—i.e., an
average day and night—is called a
mean solar daymean solar day
and takes 24 hours.
But a rotation of the Earth with respect to the
UniverseUniverse and sidereal time—i.e.,
with respect to the “universal frame” in
universalFrame—is called a
sidereal daysidereal day
and takes
approximately 23 hours and 56 minutes.
The exact value is stored in the Earth’s info table as a
rotationPeriodrotationPeriod (field of info table)
of 0.997269558333333 mean solar days.
How could we have calculated that the mean solar day
is four minutes longer than the sidereal day?
The angular distance in radians through which the Earth rotates
with respect to the universal frame in
t
days is
f(t)
=
2π
t
rotationPeriod
For example,
in one
rotationPeriod
the Earth makes one full rotation of
2π
radians because
f(rotationPeriod)
= 2π
Similarly,
the angular distance in radians through which the Earth revolves around the Sun
in
t
days is
g(t)
=
2π
t
orbitPeriod
where the
orbitPeriodorbitPeriod (field of info table)
of 365.25 mean solar days also comes from the Earth’s info table.
For example, in one
orbitPeriod
the Earth revolves a full
2π
radians because
orbitPeriod)
= 2π
In the following diagram,
the little person on the bottom Earth is experiencing noon
because the Sun is directly above his or her head.
Let’s say this happens at time
t = 0.
If the Earth remained in the same place with respect to the Sun,
the next noon at the point where he or she is standing would come when
f(t) = 2π
i.e., when the point has rotated all the way around the Earth.
Solving the above equation for t
yields
t = rotationPeriod
and the Earth is portrayed at this time in the middle picture.
But because of the Earth’s revolution around the Sun,
the next noon actually comes a bit later.
It happens when
f(t) = 2π + g(t)
where
g(t)
is the angle through which the Earth has revolved around the Sun
since the starting time.
Solving the above equation for
t
yields a value slightly longer than the
rotationPeriod:
t =
rotationPeriod
·
orbitPeriod
orbitPeriod - rotationPeriod
and the Earth is portrayed at this time in the top diagram.
The value of
t
is the length of the mean solar day.
We can solve for
t
only if the
rotationPeriod
and the
orbitPeriod
are unequal.
Were they equal,
the Earth would always keep the same side facing the Sun,
as the Moon always keeps the same side facing the Earth.
The next noon would never come and the program would
divide by zerodivision by zero.
Let’s find the
meanSolarDay:
--[[
Print the length of Earth's mean solar day.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local info = celestia:find("Sol/Earth"):getinfo()
local rotation = info.rotationPeriod
local orbit = info.orbitPeriod
assert(orbit > rotation)
--Measured in mean solar days, so tab[3][2] should be 1.
local tab = {
{"sidereal year", orbit},
{"sidereal day", rotation},
{"mean solar day", rotation * orbit / (orbit - rotation)}
}
local s = ""
for i, value in ipairs(tab) do
--Convert days to days, hours, minutes, seconds.
local dhms = std.todhms(value[2])
s = s .. string.format(
"%-14s = %17.15g days = %3dd %2dh %2dm %.15gs\n",
value[1], value[2],
dhms.days, dhms.hours, dhms.minutes, dhms.seconds)
end
celestia:print(s, 60)
wait()
end
main()
sidereal year = 365.25 days = 365d 6h 0m 0ss
sidereal day = 0.997269558333333 days = 0d 23h 56m 4.08984000000402s
mean solar day = 0.999999933396747 days = 0d 23h 59m 59.9942454789675s
Verify that a mean solar day on MercuryMercury, mean solar day of is approximately 176 Earth mean solar days.
It takes the MoonMoon, synodic period of approximately 27 days to orbit the Earth (a sidereal monthsidereal month), measured with respect to the universal frame. Use the same formula to predict how many days it will take the Moon to cycle through its phasesphases, of Moon as seen from the Earth (a synodic monthsynodic month):
local earth = celestia:find("Sol/Earth"):getinfo().orbitPeriod local moon = celestia:find("Sol/Earth/Moon"):getinfo().orbitPeriod assert(earth > moon) local synodicMonth = earth * moon / (earth - moon) sidereal year = 365.25 days = 365d 6h 0m 0s sidereal month = 27.321661 days = 27d 7h 43m 11.5103999999019s synodic month = 29.530629806842 days = 29d 12h 44m 6.41531114669988sUse the same formula to predict how long it will take VenusVenus, synodic period of to cycle through its phasesphases, of Venus as seen from the Earth (a synodic periodsynodic period):
local earth = celestia:find("Sol/Earth"):getinfo().orbitPeriod local venus = celestia:find("Sol/Venus"):getinfo().orbitPeriod assert(earth > venus) local synodicPeriod = earth * venus / (earth - venus) Seen from the Earth, it takes 583.94438669439 Earth days for Venus to go through its phases.MarsMars, synodic period of is at oppositionopposition when the Sun and Mars are in opposite directions as seen from the Earth. At this time, the Earth is directly between them. How far apart in Earth days are two successive oppositions of Mars? In other words, how long does it take Mars to cycle through its phasesphases, of Mars as seen from the Earth? Hint: the Earth is Mars’s Venus.
Why do the
tidestides
circle the Earth every 24 hours and 50 minutes?
(They actually circle twice during this period, but let’s ignore that.)
Hint: get the Earth’s
rotationPeriod
and the Moon’s
orbitPeriod.
At midnight, the hour and minute hands of a clockclock, hands of point in the same direction. The next time this will happen is a little after 1:05 a.m. Find the exact time.
How long is a mean solar day on VenusVenus, mean solar day of? Since its rotation is retrograde, you will have to invent a new formula.
A solar system object can go through one or more
phases,
each with its own shape and appearance.
For example,
a spacecraft can shed a module,
emit an exhaust,
develop a bow shock,
and pop out a parachute.
Let’s take the phases of the
HuygensHuygens (spacecraft)
spacecraft,
listed in the file
version/extras-standard/cassini/cassini.ssccassini.ssc (file).
During phase 1 it was attached to its mother ship
CassiniCassini (spacecraft).
During phase 2 it was flying free towards
SaturnSaturn, as primary of Titan’s
moon
TitanTitan (moon of Saturn).
We will begin at a point in time just before the end of phase 1.
The method
Object:phasesObject:phases
is a
factory function
that returns an
iterator
that returns an object of class
PhasePhase (class).
Since we are interested in only the first phase,
we will call the iterator only once.
t0
and
t1
are the times of the start and the end of the phase.
I wanted to name them
start
and
end,
but
“end”end (Lua keyword)
was a Lua
keywordkeyword (Lua).
See bodyfixedFrame for the fine points of the “bodyfixed” axesbodyfixed frame of reference. Our present concern is with time, not geometry. Let’s just say that Huygens departs from Cassini along the negative X axis of Cassini’s bodyfixed frame. We assume the Celestia window is landscape, so we oriented the observer to make this axis horizontal to keep Huygens in view as long as possible.
Cassini is shaped roughly like a cylinder, and the axis of this cylinder is Cassini’s Y axis. Our direction of view is perpendicular to this axis to give us a broadside view of Cassini’s body.
Thus Cassini’s X and Y axes lie in the plane of the Celestia window. These conditions make it ideal for the observer to be on Cassini’s Z axis. We place him on the negative Z axis to get slightly better lighting (the phase anglephase angle is less than 90°). To sum up, Cassini’s bodyfixed X axis points left, its Y axis points up, and its Z axis points away from the user into the window. Huygens moves off horizontally to the right.
--[[
Watch Huygens separating from Cassini at the end of the first phase
of Huygen's life.
]]
require("std")
local function main()
local observer = celestia:sane()
--Make it look realistic.
celestia:hide("constellations", "grid")
celestia:hidelabel("constellations", "globulars", "stars")
local huygens = celestia:find("Sol/Cassini/Huygens")
local iterator = huygens:phases()
assert(type(iterator) == "function")
local phase = iterator() --First call to iterator returns first phase.
assert(type(phase) == "userdata" and tostring(phase) == "[Phase]")
local t0, t1 = phase:timespan()
assert(type(t0) == "number" and type(t1) == "number")
--Huygens will separate 3 seconds after the CELESTIA logo disappears.
local seconds = std.logo + 3
local days = seconds / (24 * 60 * 60)
celestia:settime(t1 - days)
local cassini = celestia:find("Sol/Cassini")
celestia:select(cassini)
local bodyfixedFrame = celestia:newframe("bodyfixed", cassini)
observer:setframe(bodyfixedFrame)
local microlightyears = 2 * cassini:radius() / KM_PER_MICROLY
local position = celestia:newposition(0, 0, -microlightyears)
observer:setposition(bodyfixedFrame:from(position))
--Cassini Y axis points towards top of window.
observer:lookat(cassini:getposition(), bodyfixedFrame:from(std.yaxis))
wait()
end
main()
In its free-flying phase,
Huygens
should
rotaterotation (in .ssc file)
at the “7.5 revolutions per minute”
advertised in the comment in
cassini.ssc.
The
PeriodPeriod (of UniformRotation)
of the
UniformRotationUniformRotation (in .ssc file)
in that file
is measured in rotations per hour,
so change it from
0.125
to .00222222222222222
= 1 / (7.5 · 60)
and restart Celestia.
The three red marks on
Huygens
are
120°
apart.
A
C programmerC (programming language)
has a rage to do everything in a single expression.
If you share this passion,
telescope the creation of
t1
to the following.
Want to see Saturn too? The X axis of the “lock frame” (lockFrame) points from Cassini to Saturn. The Z axis points upwards, perpendicular to the plane of Cassini’s motion with respect to Saturn. Press lowercase L several times to speed up the simulation time.
celestia:hide("ecliptic", "moons") celestia:hidelabel("planets", "moons") local saturn = celestia:find("Sol/Saturn") local lockFrame = celestia:newframe("lock", cassini, saturn) observer:setframe(lockFrame) local microlightyears = 2 * cassini:radius() / KM_PER_MICROLY local position = celestia:newposition(-microlightyears, 0, microlightyears / 5) observer:setposition(lockFrame:from(position)) observer:lookat(cassini:getposition(), lockFrame:from(std.zaxis))This section is a tutorial on spherical astronomy, not on Celx programming. To help the reader visualize the Universe in several frames of reference, we take the liberty of using various features of Celx without explanation. If the code and exercises are somewhat mysterious, don’t worry: we can come back to them later. Just run the programs, look at the window, and drag on the sky when applicable.
The Sun and planets, stars and galaxies are located at wildly different distances from an observer on the Earth. But our perception of depth does not extend out to these astronomical ranges. The objects in the sky appear to lie at the same distance from us, forming the surface of a dome or hemispherecelestial hemisphere.
To point out a star or planet in the sky, it is useful to give the dome a grid of latitude and longitude. There are several systems of coördinates we can use. The simplest one takes the zenithzenith (the highest point in the sky) as its North Pole. The latitude in this system is called altitudealtitude (vs. azimuth) and is measured up from the horizon. The longitude is called azimuthazimuth and is measured clockwise (i.e., to the right) from the point on the horizon due north of the observer. The Sun rising in the east, for example, would be at altitude 0° and azimuth 90°. The zenith itself is at altitude 90° and an irrelevant azimuth. The nadirnadir (the point directly below us) is at altitude –90°, except that we’d need a transparent Earth to see it.
Our definition of azimuth is not quite complete yet. At the Earth’s North Pole, there is no point on the horizon due north of the observer. Even worse, at the South Pole every point on the horizon is north of the observer. We therefore stipulate that azimuth at the North Pole shall be measured clockwise from the meridian of 180° East, and azimuth at the South Pole measured clockwise from the Prime Meridian. This ensures that a person walking up or down the Prime Meridian will experience no sudden change in the azimuth of a celestial object when he or she arrives at a pole.
The following program displays an altazimuth coördinate grid, and the altitude and azimuth of the point towards which the observer is facing. He is positioned at the top of the atmosphereatmosphere, position observer at top of to keep the Universe visible even during the day. He initially faces the north point on the horizon with the zenith overhead. For an explanation of the altazimuth machinery, see altazimuthCoordinates. We choose a date and time that puts a familiar constellation right above the north point. We also activate altazimuth mode, in which the down and up arrow keys pitch the view vertically, and the left and right arrows yaw the view horizontally.
--[[
Display the altitude and azimuth of the direction in which the observer is
looking. To change his direction, press the arrows or drag on the sky.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
--New York City
local latitude = math.rad( 40 + (39 + 51 / 60) / 60 ) --north is positive
local longitude = math.rad(-(73 + (56 + 19 / 60) / 60)) --west is negative
--[[
The origin of the altazFrame is the center of the Earth,
just like the origin of the Earth's bodyfixed frame.
The XZ plane of the altazFrame is parallel to the plane of the horizon at NYC.
The X axis is parallel to the vector pointing east from NYC.
The Z axis is parallel to the vector pointing south from NYC.
The Y axis points from the origin through NYC.
]]
local rotation = celestia:newrotationaltaz(longitude, latitude)
local altazFrame = celestia:newframe("bodyfixed", earth, rotation)
local function tickHandler()
--Get the observer's forward vector in universal frame coordinates.
--It points in the direction in which he is looking.
local orientation = observer:getorientation()
local forward = orientation:transform(std.forward)
--Rewrite the vector in altazimuth coordinates.
forward = altazFrame:to(forward)
--Convert cartesian altazimuth coordinates to spherical.
local altaz = forward:getaltaz()
local s = string.format(
"Altitude %6.2f%s\n" .. --2 digits to right of decimal point
"Azimuth %6.2f%s",
math.deg(altaz.altitude), std.char.degree,
math.deg(altaz.azimuth), std.char.degree)
celestia:mmprint(s) --Mark the center of the window with "MM".
end
local function main()
celestia:hide("grid") --Hide the right ascension and declination.
celestia:show("horizontalgrid"horizontalgrid (renderflag)) --altazimuth grid
celestia:setaltazimuthmode(true)
celestia:select(earth)
--Ripe, low-slung Big Dipper above daylit northern horizon.
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
celestia:settime(celestia:utctotdb(year, 1, 29, 20, 23, 0.0))
observer:setframe(altazFrame)
--Top of the atmosphere, so we don't have to worry about day and night.
local kilometers = earth:radius() + earth:getinfo().atmosphereHeight
local microlightyears = kilometers / KM_PER_MICROLY
local position = celestia:newposition(0, microlightyears, 0)
observer:setposition(altazFrame:from(position))
--Look straight north along the horizon, zenith overhead.
local forward = celestia:newvectoraltaz(math.rad(0), math.rad(0))
local up = celestia:newvectoraltaz(math.rad(90), math.rad(0))
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(altazFrame:from(orientation))
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
MM
Altitude -0.00°
Azimuth 0.00°
Verify that the observer is above New York City.
Press the up arrow to face straight down to the nadir
(altitude
–90°).
Then press
EndEnd key
to move far enough away from the Earth to see the Atlantic seaboard.
Come back to Earth with
HomeHome key.
Verify that the altitude of the North StarNorth Star, altitude of in the sky is equal to the latitude of the observer on the Earth. Since he is above New York City at approximately 40° North, you can press the down arrow to pitch his view up to altitude 40°. Then press three lowercase Ls to speed up time, and three lowercase Ks to slow it back down.
Try another city, or another latitude and longitude.
Is the horizontal grid rendered correctly when the observer is
directly above a pole?
See the member function
Renderer::renderSkyGrids
in
version/src/celengine/render.cpp.
What is the azimuth of the rising sun on the first day of spring at sea level in New York City? Sunrise on that date is approximately 6:00 UTC at Greenwich, and 1/360 of a day later for each degree of longitude west of there. In New York, for example, the sun rises 74/360 of a day later. celestia:settime(celestia:utctotdb(year, 3, 21, 6) + 74/360) The surface of the Earth jittersjitter (of planetary surface) annoyingly at sea level, so position the observer a few meters higher: local kilometers = earth:radius() + .01 --10 meters above sea level Look East by facing towards azimuth 90°. local forward = celestia:newvectoraltaz(math.rad(0), math.rad(90)) Press lowercase L to fast-forward to the exact moment of sunrise, the freeze the simulation time with the spacebar. In altazCelobject, we’ll get the altitude and azimuth of a celestial object without the need for trial and error. In whenSunset, we’ll get the exact time of sunrise.
Seen from the center of StonehengeStonehenge, the HeelstoneHeelstone (Stonehenge) is at azimuth (360/7)°. Does the rising Sun line up with the stone on the first day of summer? Check out the other henges: ManhattanhengeManhattanhenge, MITHengeMITHenge, etc.
Does your initial azimuth
jitterjitter (of numeric value)
between
0.00
and
360.00?
It’s because a number in the range
359.995
to 360 inclusive
is formatted by
"%6.2f"
as the string
"360.00".
Intercept any number in this range and change it to zero:
local azimuth = math.deg(altaz.azimuth)
if azimuth >= 359.995 then
azimuth = 0
end
--Now format the azimuth with "%6.2f".
Does your initial altitude jitter between
0.00
and
-0.00?
It’s because a negative number greater than
–.005
is formatted by
"%6.2f"
as the string
" -0.00".
Intercept any number in this range and change it to zero:
local altitude = math.deg(altaz.altitude)
if altitude > -.005 and altitude < 0 then
altitude = 0
end
--Now format the altitude with "%6.2f".
The above program positions the observer
well above the visible
atmosphereatmosphere, scattering of light by,
even though it takes the
atmosphereHeight
from the Earth’s info table
(infoTable).
In fact,
Celestia renders an atmosphere only as high as the altitude where the scattering
of light is only
5%
of the surface value.
See
Object:setatmosphereObject:setatmosphere
and change the observer’s altitude to the following.
Print the observer’s azimuth as a cardinal direction as well as an angle. Create the following table of 16 strings at the top of the program, outside of any function. (It’s not an array because the keys do not begin with 1.)
--variables used by tickHandler: local direction = { [0] = "north", --first key is 0 "north by northeast", "northeast", "east by northeast", "east", "east by southeast", "southeast", "south by southeast", "south", "south by southwest", "southwest", "west by southwest", "west", "west by northwest", "northwest", "north by northwest" --last key is 15 } local n = #direction + 1 --the number of strings (16)
Insert the following code immediately before printing the string
s
in the tick handler.
The
altaz.azimuth
is the range 0 to almost 2π.
We can reduce it to the range 0 to almost 1 by dividing it by 2π.
Then we blow it back up to the range 0 to almost
n
by multiplying it by
n.
Roundedstd.round
to the closest whole number,
it can be used as a key in the table.
If the Earth became transparent,
or if we pressed
control-w
for the OpenGL
wireframe modewireframe mode (OpenGL),
we would see the entire
celestial
sphere
that
Olaf StapledonStapledon, Olaf
envisioned.
Our tiny Earth is located at the center of the sphere.
From the Earth, we look outwards towards the inner surface of the sphere.
The 88 constellationsconstellations cover the surface of the sphere as the oceans and continents cover the surface of the Earth. Each constellation is a convenient name for a direction, or a bundle of directions, in which we can look from the Earth. The constellation of Ursa MinorUrsa Minor, for example, includes the direction from the center of the Earth towards the Earth’s North Pole. SagittariusSagittarius includes the direction from the Earth towards the center of our galaxy. The borderlandTaurus/Gemini of GeminiGemini and TaurusTaurus includes the direction from the Earth towards the Sun on the first day of each year’s summer in the Earth’s northern hemisphere.
Let’s look past the Earth
towards the inner surface of the celestial sphere.
We will pick a vantage point above the
subsolar meridiansubsolar meridian,
the line of longitude that goes through the
subsolar point
on the surface of the Earth.
See
lockFrame
for the lock frame
and
erect
for the
Vector:erect.
We will fast-forward through one
rotation of the EarthEarth, rotation of
with an abrupt start and end.
See
gradualStart
to make the Earth pick up speed gradually.
--[[
Watch one rotation of the Earth at high speed. The tickHandler holds the
observer above the point where the subsolar meridian crosses the equator.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
--simulation time of end of fast-forward: 1 day after logo disappears
local t1 = celestia:gettime() + std.logo / (60 * 60 * 24) + 1
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
local lockFrame = celestia:newframe("lock", earth, sol)
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local function tickHandler()
--Go back to the normal time scale after one day of simulation time.
if celestia:gettime() >= t1 then
celestia:settimescale(1)
end
--toNorthPole is a unit vector in universal coordinates
--from center of Earth towards North Pole of Earth.
local toNorthPole = bodyfixedFrame:from(std.yaxis)
--toSol is a unit vector in universal coordinates
--from center of Earth towards center of Sun.
local toSol = lockFrame:from(std.xaxis)
--v is a unit vector in universal coordinates in plane of toNorthPole
--and toSol, and perpendicular to toNorthPole.
local v = toNorthPole:erect(toSol)
local position = earth:getposition()
observer:setposition(position + microlightyears * v)
observer:lookat(position, toNorthPole)
end
local function main()
--clouds distracting, ecliptic irrelevant
celestia:hide("cloudmaps", "cloudshadows", "ecliptic")
celestia:show("boundaries") --of constellations
celestia:hidelabel("planets") --We know the Earth is the Earth.
--Pass a table to a method. Don't need parentheses around the table.
earth:addreferencemark({type = "body axes"})
earth:addreferencemark({type = "planetographic grid"})
--earth:addreferencemark({type = "sun direction"})
observer:setframe(lockFrame)
celestia:registereventhandler("tick", tickHandler)
--Wait till the "CELESTIA" logo disappears before starting fast-forward.
wait(std.logo)
--one hour of simulation time per second of real time
celestia:settimescale(60 * 60)
wait()
end
main()
Equivalently, we can think of the Earth as remaining motionless at the center of the celestial sphere. The sphere would then rotate around the Earth once per day, as the world spins around a person standing on a Lazy Susan. Let’s fast-forward through one rotation, hovering in geostationary orbitgeostationary orbit over the point at latitude 0° longitude 0° off the west coast of Africa.
--[[
Watch one rotation of the Earth while hovering over the South Atlantic.
]]
require("std")
--variable used by tickHandler:
local t1 = celestia:gettime() + std.logo / (60 * 60 * 24) + 1
local function tickHandler()
--Go back to the normal time scale after one day of simulation time.
if celestia:gettime() >= t1 then
celestia:registereventhandler("tick", nil)
celestia:settimescale(1)
end
end
local function main()
local observer = celestia:sane()
--clouds distracting, ecliptic irrelevant
celestia:hide("cloudmaps", "cloudshadows", "ecliptic")
celestia:hidelabel("planets") --We know the Earth is the Earth.
local earth = celestia:find("Sol/Earth")
earth:addreferencemark({type = "spin vector"}) --Earth's axis
earth:addreferencemark({type = "sun direction"}) --Dress up subsolar pt.
--Show the terminator (border of day and night) as a yellow line.
earth:addreferencemark({
type = "visible region",
target = celestia:find("Sol")
})
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
local position = celestia:newpositionlonglat(
math.rad(0), --longitude: on the prime meridian
math.rad(0), --latitude: on the equator
6 * earth:radius() / KM_PER_MICROLY)
observer:setposition(bodyfixedFrame:from(position))
--Face the center of the Earth, with Earth's North Pole at the top.
observer:lookat(earth:getposition(), bodyfixedFrame:from(std.yaxis))
wait(std.logo) --until "CELESTIA" logo disappears
celestia:registereventhandler("tick", tickHandler)
--one hour of simulation time per second of real time
celestia:settimescale(60 * 60)
wait()
end
main()
Is
PolarisPolaris (star)
really the
North Star?
Let the observer hover over Antarctica by changing his latitude to
math.rad(-90).
To reduce the area of the sky blocked by the Earth,
increase the distance to 12 or more times the Earth’s radius.
You could also toggle the OpenGL wireframe mode with
control-w
to let
Polaris
shine through the Earth.
Set the above program to 2788 B.C., when the pole star was ThubanThuban (star) (α Draconis). Since there was no year 0 A.D., the argument –2787 takes us to 2788 B.C.
--North Pole closest to Thuban on August 24 2788 B.C., 1:00 a.m. UTC celestia:settime(celestia:utctotdb(-2787, 8, 24, 1)) celestia:select(celestia:find("Thuban"))The North Star of the Earth is Polaris. Verify that the South Star of SaturnSaturn, South Star of is δ Octantisδ Octantis (star).
We just saw the celestial sphere rotating around a stationary Earth. Like any rotating sphere, it has a north polenorth celestial pole, south pole, and equatorcelestial equator. An observer standing at the North Pole of the Earth would see the north pole of the celestial sphere directly overhead. An observer on the Earth’s equator would see a point on the celestial sphere’s equator overhead.
Given the north pole and equator of the celestial sphere, we can mark out another system of latitude and longitude on it. The latitude is called declination and is measured north and south from the celestial equator. The longitude is called right ascension and is measured counterclockwise from a meridian on the celestial sphere that goes through a point in the constellation PiscesPisces. This point is the vernal equinoxvernal equinox, the direction from the Earth to the Sun on the first day of spring in the Earth’s northern hemisphere. In the same way, east longitude on Earth is measured counterclockwise from a meridian on the terrestrial sphere that goes through a point in Greenwich, EnglandGreenwich, England. Right ascension goes from 0 to almost 360°. Celx expresses this range as 0 to almost 2π radians (radians). Human beings express it as 0 to almost 24 hours (hours), abbreviated with a superscript “h”.
For example, Pisces itself is at Right Ascension 0h and Declination 0°. (It’s like the famous point off the west coast of Africa at longitude 0° East and latitude 0° North). The constellation group Taurus/GeminiTaurus/Gemini, 90° counterclockwise from Pisces, is at Right Ascension 6h and Declination 23° North. (It’s like Bangladesh at longitude 90° East and latitude 23° North). The North StarNorth Star in Ursa MinorUrsa Minor is at an almost irrelevant right ascension and a declination of almost 90° North. (It’s like the Earth’s North Pole at an irrelevant longitude and latitude 90° North.)
The right ascension and declination coördinates are known as the J2000 equatorial coördinates. Do not confuse them with the “equatorial frames” in equatorialFrame. One complication: the Earth’s axis points in different directionsprecession of Earth’s axis at different times, moving the north celestial pole along the surface of the celestial sphere. The J2000 means that the equatorial coördinates were defined using the Earth’s axis as it was on January 1, 2000 at noon UTC. (The J stands for Julian, not January.)
The geographical convention is to cite the latitude followed by the longitude
(despite the Celx method
Observer:gotolonglat).
The astronomical convention
is to cite the right ascension followed by the declination.
Thus
BetelgeuseBetelgeuse (star)
is at
RA 5h 55m
Dec
+7°
24′.
The following program displays the right ascension and declination of the direction in which the observer is facing. The right ascension is displayed in hours, minutes and seconds (hours); the declination in degrees, minutes, and seconds (degrees). For the frames of reference, see rotatedRadec.
--[[
Display the right ascension and declination of the direction in which the
observer is facing. To change his direction, press the arrows or drag on the
sky.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local radecFrame = celestia:newframe("universal", std.radecRotation)
local function tickHandler()
--Get the observer's forward vector in universal frame coordinates:
--X axis points towards Pisces, Y axis towards Draco.
local forward = observer:getorientation():transform(std.forward)
--Rewrite the vector in radecFrame coordinates:
--X axis points towards Pisces, Y axis towards Polaris.
forward = radecFrame:to(forward)
--Convert Cartesian coordinates to spherical.
local longlat = forward:getlonglat()
--Break down radians into conventional units.
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
local s = string.format(
"RA %dh %dm %.2fs\n"
.. "Dec %s%d%s %d%s %.2f%s",
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
celestia:mmprint(s)
end
local function main()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
--Look towards RA 6h Dec +23 degrees in Gemini/Taurus,
--with north pole of the ecliptic in Draco directly overhead.
local forward =
celestia:newvectorradec(math.rad(360 * 6 / 24), std.tilt)
local up = celestia:newvectorradec(math.rad(360 * 18 / 24),
math.rad(90) - std.tilt)
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(orientation)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
MM
RA 6h 0m 0.00s
Dec +23° 26′ 21.45″
The unit vector pointing forward to Taurus/Gemini may be written in any of the following ways. Which is simplest?
celestia:newvectorradec(math.rad(360 * 6 / 24), std.tilt) celestia:newvector(0, 0, -1) -std.zaxis std.forwardThe unit vector pointing straight up to DracoDraco may be written in any of the following ways. Which is simplest?
celestia:newvectorradec(math.rad(360 * 18 / 24), math.rad(90) - std.tilt) celestia:newvector(0, 1, 0) std.yaxis std.upThe initial right ascension in the above program is 6h 0m 0.00s. When you press the down arrow and pitch upwards, do you ever get an annoying right ascension of 5h 59m 60.00s? If so, intercept the 60.00s before it is printed. See the jitter examples in celestialDome. if ra.seconds > 59.995 then ra.seconds = 0 ra.minutes = ra.minutes + 1 if ra.minutes == 60 then ra.minutes = 0 ra.hours = ra.hours + 1 if ra.hours == 24 then ra.hours = 0 end end end And similarly for declination: if dec.seconds > 59.995 then dec.seconds = 0 dec.minutes = dec.minutes + 1 if dec.minutes == 60 then dec.minutes = 0 dec.degrees = dec.degrees + 1 assert(dec.degrees <= 90) end end
The J2000 equatorial coördinate system can be provided with the following Cartesian axes. The XZ plane is the plane of the celestial equator. The X axis points towards the vernal equinox at RA 0h in Pisces. This is the direction from the Earth towards the Sun on the first day of spring in the Earth’s northern hemisphere. The Z axis points towards RA 18h in the constellation OphiuchusOphiuchus. The Y axis points towards the north celestial pole near Polaris.
The following diagram looks down from Polaris onto the XZ plane. The Y axis points straight up towards us and is invisible.
It takes a full year for the Earth to revolveEarth, orbit of around the Sun. Let’s fast-forward through the current hour of the current year.
The following program positions the observer slightly beyond the orbit of the Earth, shown as a horizontal red line. The Earth will travel from left to right along the orbit as we look inwards towards the Sun. Satisfy yourself that the Earth circles the Sun counterclockwise when viewed from above the Earth’s north pole, looking down at the Earth. We can uncomment the planetographic grid to spruce up the dark side of the Earth.
--[[
Watch the Earth revolve around the Sun for one hour of simulation time.
Keep the Earth's orbit horizontal.
]]
require("std")
--variables used by tickHandler:
local minutes = 60 --fast forward through this number of minutes
local days = minutes / (24 * 60) --fast forward through this number of days
--times of start and end of fast-forward
local t0 = celestia:gettime() + std.logo / (60 * 60 * 24) - days / 2
local t1 = t0 + days
local function tickHandler()
if celestia:gettime() >= t1 then
celestia:registereventhandler("tick", nil)
celestia:settimescale(1)
end
end
local function main()
local observer = celestia:sane()
--When the Earth is selected, make its orbit visible.
--Show no other lines.
celestia:hide("grid", "ecliptic")
celestia:show("orbits")
celestia:hidelabel("planets") --We know that the Earth is the Earth.
--No other orbit should be visible.
celestia:setorbitflagsCelestia:setorbitflags({Planet = false, Moon = false})
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
celestia:select(earth) --Make Earth's orbit red.
--earth:addreferencemark({type = "planetographic grid"})
--Observer looks sunwards from a point 12 radii beyond Earth's orbit.
local lockFrame = celestia:newframe("lock", earth, sol)
local microlightyears = 12 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
--Orient the observer so that the axis of the Earth's orbit points up.
observer:lookat(sol:getposition(), std.yaxis)
celestia:settime(t0)
wait(std.logo) --until "CELESTIA" logo disappears
celestia:registereventhandler("tick", tickHandler)
--3 minutes of simulation time per second of real time
celestia:settimescale(60 * 3)
wait()
end
main()
Don’t hardwire the number of microlightyears into the above program.
Let it program compute how far out from the Earth’s orbit
the observer would have to be
to make the Earth go across the window during one hour of simulation time.
local daysInYear = earth:getinfo().orbitPeriod
local minutesInYear = daysInYear * 24 * 60
--circumference in astronomical unitsastronomical unit of Earth's orbit
local circumference = 2 * math.pi
--length in astronomical units of arc traveled in minutes/2 minutes.
local arc = circumference * (minutes / 2) / minutesInYear
--Assume the arc is practically a straight line.
local tangent = math.tanmath.tan(observer:gethorizontalfov() / 2)
assert(tangent > 0)
local farOut = arc / tangent --in astronomical units
--Convert astronomical units to microlightyears.
local microlightyears = farOut * std.microlyPerAu
Could we get greater accuracy by using the Earth’s current distance from the Sun? Or by acknowledging that the arc is curved?
Consider a point on the Earth’s equator. What makes a bigger contribution to its speed with respect to the Sun: the Earth’s rotation around its axis, or the Earth’s revolution around the Sun?
The previous program showed the Earth revolving around a stationary Sun. In another frame of reference, the Sun would revolve around a stationary Earth. The Earth would still rotate around its axis, but the center of the Earth would remain motionless.
From the point of view of this Earth,
the Sun would make an annual counterclockwise circle,
called the
ecliptic,
along the surface of the celestial sphere.
The ecliptic is a
great circlegreat circle,
the same size as the celestial equator
but tilted about
23°
therefrom.
(The exact angle in radians is
std.tiltstd.tilt.)
The
north pole of the eclipticnorth pole of ecliptic
is in the constellation
DracoDraco,
23°
from the
north
celestial polenorth celestial pole
near
PolarisPolaris (star).
The
south pole of the eclipticsouth pole of ecliptic
is in the constellation
DoradoDorado,
23°
from the
south
celestial polesouth celestial pole
in
OctansOctans.
Let’s watch the Sun travel along the
ecliptic
as we fast-forward through 48 days.
The ecliptic appears as a straight line
because the celestial sphere is projected
onto the window with a
gnomonic
projectiongnomonic projection,
in which all great circles appear as straight lines.
The constellations through which the ecliptic passes are called the
zodiaczodiac;
their names are listed in
std.zodiacstd.zodiac.
We’ll give them the same red color as the ecliptic,
the
Renderer::EclipticColorRenderer::EclipticColor (C++ constant)
in
version/src/celengine/render.cpp.
--[[
Watch the Sun travel along the ecliptic for 48 days of simulation time.
Keep Polaris overhead.
]]
require("std")
--variables used by tickHandler:
local days = 48 --fast forward through this number of days
--times of start and end of fast-forward
local t0 = celestia:gettime() + std.logo / (60 * 60 * 24) - days / 2
local t1 = t0 + days
local function tickHandler()
if celestia:gettime() >= t1 then
celestia:registereventhandler("tick", nil)
celestia:settimescale(1)
end
end
local function main()
local observer = celestia:sane()
celestia:hide("grid") --right ascension and declination
celestia:show("eclipticgrid") --ecliptic latitude and longitude
celestia:hidelabel("planets") --We know that the Earth is the Earth.
--Make the zodiac the same color as the ecliptic.
celestia:setconstellationcolor(.5, .1, .1, std.zodiac)
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local eclipticFrame = celestia:newframe("ecliptic", earth)
observer:setframe(eclipticFrame)
local lockFrame = celestia:newframe("lock", earth, sol)
local microlightyears = 12 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
--Orient the observer so that the Earth's axis points up.
local equatorialFrame = celestia:newframe("equatorial", earth)
observer:lookat(sol:getposition(), equatorialFrame:from(std.yaxis))
celestia:settime(t0)
wait(std.logo) --until "CELESTIA" logo disappears
celestia:registereventhandler("tick", tickHandler)
--one day of simulation time per 2 seconds of real time
celestia:settimescale(60 * 60 * 24 / 2)
wait()
end
main()
The above program shows the Sun moving along the ecliptic
on the current date.
Watch it on the first day of spring in the northern hemisphere of Earth.
Insert the following statements immediately before creating
t0.
In the spring,
the Sun moves along the part of the ecliptic
that crosses the celestial equator in
Pisces,
going uphill at an angle of
23°.
To see the angle,
do not
hide
the
"grid"
and do not
show
the
"eclipticgrid".
The exact point at which the ecliptic crosses the equator
is hidden by the Earth in this program.
It is called the
vernal
equinoxvernal equinox
and is located in the constellation
PiscesPisces.
This crossing marks the start of spring.
Watch the Sun on the first day of summer, fall, and winter, too. See the diagram of the plane of the ecliptic in universalFrame, also known as “the XZ plane of the universal frame”.
The above exercise showed that the Sun crosses the celestial equator twice a year.
The great circle formed by the meridians of 0h and 12h on the celestial sphere is called the equinoctial colureequinoctial colure. Perpendicular to it, the great circle formed by the meridians of 6h and 18h is called the solstitial coluresolstitial colure. The colures are perpendicular to the celestial equator and intersect at the north celestial polenorth celestial pole near PolarisPolaris (star).
The solstitial colure will be of greater importance to us because by defaultorientation, default the observer faces towards a point on it. This colure goes through the following four points. They will be our landmarkslandmarks (on celestial sphere). Memorize them.
|
|
| DracoDraco (north pole of eclipticecliptic), at RA 18h Dec +67° By default, this is the observer’s zenithzenith. ↑ 23° ↓ Polaris (north pole of celestial equatorcelestial equator), at RA <irrelevant> Dec +90° ↑ | | 67° | | ↓ Taurus/GeminiTaurus/Gemini (the summer solsticesummer solstice), on the ecliptic at RA 6h Dec +23° By default, the observer faces towards this point. ↑ 23° ↓ OrionOrion, on the celestial equator at RA 6h Dec 0° | | |
The following program displays
the part of the solstitial colure that contains the four points.
The colure is the vertical line down the middle of the window.
When the observer faces a landmark,
we will highlight it by doubling the
Renderer::ConstellationColorRenderer::ConstellationColor (C++ constant)
in
version/src/celengine/render.cpp.
--[[
Visit and highlight our four landmarks along the solstitial colure.
Press the up and down arrows or drag on the sky.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local radecFrame = celestia:newframe("universal", std.radecRotation)
local constellationError = math.rad(5)
local printError = math.rad(2)
local landmarks = {
{0, {"Orion"}, "celestial equator"},
{std.tilt, {"Gemini", "Taurus"}, "summer solstice"},
{math.pi / 2, {"Ursa Minor"}, "north celestial pole"},
{math.pi / 2 + std.tilt, {"Draco"}, "north pole of ecliptic"}
}
local function tickHandler()
--Unit vector in universal coordinates
--along which the observer is looking.
local forward = observer:getorientation():transform(std.forward)
--[[
Let the observer pitch up and down the solstitial colure, but don't let
him yaw left and right. If he tries to yaw, make his forward vector
point at the closest point on the colure. If there is no closest point,
point towards Taurus/Gemini.
]]
if (forward ^ std.xaxis):length() == 0 then
forward = -std.zaxis --Taurus/Gemini
else
forward = std.xaxis:erect(forward)
end
--Point the observer along the new forward vector,
--with the X axis of the universal frame pointing to his right.
observer:lookat(observer:getposition() + forward, std.xaxis ^ forward)
--Get the RA, Dec coordinates of the observer's forward vector.
local longlat = radecFrame:to(forward):getlonglat()
--Break down radians into conventional units.
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
local s = string.format(
"RA %dh %dm %.2fs\n"
.. "Dec %s%d%s %d%s %.2f%s",
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
--how far north of Orion
local theta = math.atan2(forward:gety(), -forward:getz()) + std.tilt
for i, landmark in ipairs(landmarks) do
if math.abs(theta - landmark[1]) < constellationError then
--Highlight the set of constellations.
celestia:setconstellationcolor(2 * 0, 2 * .24, 2 * .36,
landmark[2])
else
--Go back to original color.
celestia:setconstellationcolor(0, .24, .36, landmark[2])
end
if math.abs(theta - landmark[1]) < printError then
s = s .. "\n" .. landmark[3]
end
end
celestia:print(s, 60, 0, 0, 0, 0) --center of window
end
local function main()
--Put the Sun behind us,
--so it doesn't block our view of the summer solstice.
observer:setposition(celestia:newposition(0, 0, -1))
celestia:print("Press the up and down arrows.", std.logo, 0, 0, 0, 0)
wait(std.logo)
celestia:registereventhandler("tick", tickHandler)
end
main()
RA 6h 0m 0.00s
Dec 23° 26′ 21.45″
summer solstice
We now have three systems of coördinates we can impose on the celestial sphere.
The planes of the equators of the equatorial and ecliptic systems
are separated by an angle of
23°
(std.tilt).
The same angle separates the north pole of the
celestial equator
near
Polaris
from the north pole of the
ecliptic
in
Draco.
Later we will have additional systems of coördinates, the galactic and supergalactic in galacticCoordinates and supergalacticCoordinates. And we could easily invent more of them. Imagine a system whose north pole is the radiant point of the Perseid meteor showerPerseid meteor shower, or the solar apexsolar apex, or the warmest spot in the cosmic microwave background radiationcosmic microwave background radiation. We will draw their grids in traceRetrograde.
The distinction we made in
time
between simulation time and real time
corresponds to the one we now make between simulation space and real space.
Simulation spacesimulation space
is home to the observer,
who roams across the lightyears of the Celestia universe.
Real spacereal space
is home to his alter ego,
the user, who remains fixed at a point
400 millimeters (about 16 inches)
in front of the Celestia window.
This default is set by the
distanceToScreendistanceToScreen (C++ variable)
in
version/src/celestia/celestiacore.cpp
and the
REF_DISTANCE_TO_SCREENREF_DISTANCE_TO_SCREEN (C++ variable)
in
version/src/celengine/render.cpp.
It can be changed with
Observer:setfovObserver:setfov,
since a wider
field of view
pulls the user closer to the window.
The distance can also be changed in a Celestia compiled
--with-kdeKDE (K Desktop Environment)
by selecting
Settings →
Configure Celestia… →
Viewing Distance.
A third kind of space is the domain of the OpenGL graphics in
opengl.
It remains two-dimensional unless we call
gl.Frustumgl.Frustum
and
glu.LookAtglu.LookAt.
A fourth kind of space is the underworld where Celestia goes
when it
divides by zerodivision by zero.
But the primary space of Celestia is simulation space,
to which the rest of
§11
is devoted.
The position of an observer or a celestial object
is measured with respect to a Celx
frame of referenceframe of reference.
A frame has three perpendicular
axesaxis (of frame of reference)
meeting at an
originorigin (of frame of reference).
The unit of distance along all three axes is the
microlightyear
in
lightyear.
The same unit is used by all frames:
the
Lorentz-FitzGerald
contractionLorentz-FitzGerald contraction
does not occur in Celestia.
The scale remains constant:
a frame does not supply the
comoving
coördinatescomoving coördinates
with which cosmologists describe the
expansion of the UniverseUniverse, expansion of.
And all frames share the same time:
EinsteinEinstein, Albert’s
twin paradoxtwin paradox
does not arise in Celestia.
Note, however, that it is possible for different observers
to inhabit different points in time;
see
Celestia:synchronizetimeCelestia:synchronizetime.
A Celx frame is right-handedright-handed frame, a convention inherited from the OpenGLOpenGL and right-handedness graphics library. This means that when the X axis points to our right and the Y axis points up, the Z axis will point towards us. To illustrate right-handedness, the following diagram looks down on the XY plane of a frame of reference. Since the frame is right-handed, the Z axis is determined by the other two axes. It points straight up towards us and is invisible in the diagram.
The fundamental planefundamental plane (of frame) of a frame of reference is the plane where most of the action is. The XY plane is the fundamental plane for two sets of frames: the chase frames in chaseFrame and the lock frames in lockFrame. But all of the other frames prefer the XZ plane, shown in the following diagram. Since the frame is right-handed, the Y axis points straight up towards us and is invisible.
Given a point with Cartesian coördinates (x, y, z), we may need to find its spherical coördinates. But first we have to decide on names for them. Since there are so many conventions (latitude vs. colatitude, right ascension vs. azimuth, θ vs. φ), we will fall back on the standard names latitude, longitude, and distance. The latitude will be an angle in radians measured up or down from the XZ plane. The longitude will be an angle in radians in the XZ plane, measured counterclockwise from the positive X axis. The distance will be in microlightyears from the origin.
The standard library methods
Position:getlonglatPosition:getlonglat
and
Vector:getlonglatVector:getlonglat
convert the Cartesian coördinates of a position or vector to spherical.
The methods
Celestia:newpositionlonglatCelestia:newpositionlonglat
and
Celestia:newvectorlonglatCelestia:newvectorlonglat
convert spherical coördinates back to Cartesian
and deposit them in a new object.
An angle in radians that represents a right ascension or declination
may be broken down into conventional units by
std.torastd.tora
and
std.todecstd.todec.
The resulting numeric values are nonnegative,
with one exception.
The field
dec.signum
is one of the numbers 1, 0, or
–1
to indicate north, equator, or south.
The function
std.signstd.sign
returns one of the strings
"+",
"",
or
"-".
Spatium absolutumabsolute space natura sura absq; relatione ad externum quodvis semper manet similare & immobile;
Absolute Space, in its own nature, without regard to any thing external, remains always similar and immovable.
The simplest Celx frame is the universal frame. Its origin is the barycenterbarycenter (of Solar System) (center of mass) of the Solar SystemSolar System, universal frame and, always in or near the Sun. In the Celestia universe, the universal frame is “at rest”. The Solar System does not orbit the Galactic Center, the Milky WayMilky Way, approach towards Andromeda of is not approaching the Andromeda GalaxyAndromeda Galaxy (M31), and the Local GroupLocal Group (of galaxies) does not recede from the Virgo ClusterVirgo Cluster (of galaxies). If Celestia had the cosmic microwave background radiationcosmic microwave background radiation, it would be isotropic with respect to the universal frame.
Ancient versions of Celestia
had a different origin,
one
milliparsec
from the Sun—about 206
astronomical
units—in the direction of the
autumnal
equinoxautumnal equinox
in
VirgoVirgo.
This distance still shows up when you press the
Follow Earth button in a Celestia compiled
--with-kdeKDE (K Desktop Environment).
The XZ plane of the universal frame is the plane of the eclipticecliptic (theecliptic). This is the plane of the Earth’s orbit around the Sun and the plane of the Sun’s apparent orbit around the Earth. The axes are defined in terms of the locations of the equinoxes and solstices on January 1, 2000 at noon TTTT (Terrestrial Time) (Terrestrial TimeTerrestrial Time, stepThrough).
Looking down at the XZ plane from Draco, the positive Y axis points straight towards us and is invisible. The Sun remains near the origin. On approximately March 21 of each year, the Earth is to the left of the origin and the line from the Earth towards the Sun points towards Pisces. On April 21 the Earth is to the lower left of the origin, and the line from the Earth towards the Sun points towards AriesAries.
The constellations in the diagram have been spaced at equal intervals like the numbers on a clock. In the real sky they are somewhat irregular. For example, the summer solstice is in between Taurus and Gemini.
Position (class)A position object holds the Cartesian x, y, z coördinates of a position in the simulated universe. Each coördinate is stored in 128-bit fixed point format (positionCoordinates) and the unit of distance is the microlightyear (linearDistance). For the time being, the position is measured with respect to the universal frame. This will change in otherFrames when we get to the other frames.
The initial position of the observer is at the origin of the universal frame, in or near the Sun. That’s a dangerous place to be. To get away from the glare, the following program repositions him one microlightyear away from the origin, at a point on the positive Z axis of the universal frame.
In his
initial orientationorientation, initial,
the observer looks along the negative Z axis out towards
z = –∞,
with the north pole of the ecliptic in
DracoDraco
overhead at his
zenithzenith.
As long as he stays in this orientation,
the Sun will remain reassuringly in view
from his new position on the positive Z axis.
The convention of looking along the negative Z axis,
with the positive Y axis pointing up,
is inherited from
OpenGLOpenGL and initial orientation.
When we discuss “vectors” in
vectors,
we will say that his orientation’s
forward vectorforward vector of orientation
is the negative Z axis,
and its
up vectorup vector of orientation
is the positive Y axis.
Unit vectorsunit vector
(of length 1)
in these directions are available as
std.forwardstd.forward
and
std.upstd.up.
Beyond the Sun, we see the summer solsticesummer solstice at RA 6h Dec +23° in Taurus/GeminiTaurus/Gemini. Below them, OrionOrion completes Celestia’s signature triosignature trio of constellations. The X axis points towards PiscesPisces, out of the window to the observer’s right. The Y axis points up towards Draco, out of the window at the observer’s zenith. The Z axis points through the observer towards SagittariusSagittarius, out of the window to the observer’s rear.
The coördinates of the position passed to
Observer:setpositionObserver:setposition
are always measured with respect
to the universal frame,
even if the observer has been
“adhered”
to a different frame with
Observer:setframeObserver:setframe
(eclipticFrame).
The same is true for a position returned by
Observer:getpositionObserver:getposition.
--[[
Position the observer a safe distance from the Sun.
He will still be well within the orbit of Mercury.
]]
require("std")
local function main()
local observer = celestia:sane()
--One microlightyear from Solar System Barycenter
--towards the winter solstice in Sagittarius:
local position = celestia:newposition(0, 0, 1)
assert(type(position) == "userdata" and
tostring(position) == "[Position]")
observer:setposition(position)
wait()
end
main()
Our standard position
(0, 0, 1)
is in the library as
std.positionstd.position.
Use it in the above program place of the local
position.
Locate
std.position
in the above diagram.
At that position,
does the Sun block our view of
Taurus/Gemini?
Verify that
Observer:setposition
worked correctly
with the following call to
Observer:getposition.
An easier way to print a position is with
Position:getxyzPosition:getxyz.
Since it returns
more than one valuereturn values, multiple,
it can only be the
last
argument of
string.formatstring.format.
An individual coördinate of a position can be accessed in three ways.
We will demonstrate with the
x
coördinate;
the others are the same.
The square brackets seem redundant until we see their real purpose: to let us loop through the coördinates with an iterator.
local s = "" for c in std.xyzstd.xyz() do
assert(type(c) == "string")
s = s .. string.format("position.%s = %.15g\n", c, position[c])
end
position.x = 0
position.y = 0
position.z = 1
The observer adheresadherence of observer to frame to a frame. This means that he remains at the same position and orientation with respect to the frame, until disturbed by the user. Let’s verify that the frame to which he initially adheres is the universal frame.
local frame = observer:getframe() assert(type(frame) == "userdata" and tostring(frame) == "[Frame]") local name = frame:getcoordinatesystem() assert(type(name) == "string") local s = "The observer's frame is the " .. name .. " frame." The observer's frame is the universal frame.Verify that the observer remains at the same position and orientation with respect to his frame. Fast forward interactively with the keys lowercase L and K, or with the following statement. --Fast-forward one year of simulation time per second of real time. celestia:settimescale(60 * 60 * 24 * 365.25) Note that the Solar System Barycenter remains anchored in front of the observer, blocking his view of the summer solstice in Taurus/Gemini. Then speed through time fast enough to make the Sun swing around the barycenter like a star with extrasolar planetsextrasolar planet.
Although a 128-bit position coördinate (positionCoordinates) has a higher level of precision than a conventional double (doubleArithmetic), it has a narrower range of values. For example, a double whose absolute value is greater than 253 − 1 253 · 263 = 263 – 210 = 9,223,372,036,854,774,784 results in garbage when copied into a coördinate of a position object. Let’s try that value and the next double value, which is 252 253 · 264 = 263 = 9,223,372,036,854,775,808
local good = celestia:newposition(2^63 - 2^10, 0, 0) local bad = celestia:newposition(2^63, 0, 0) local s = string.format( "good = (%.19g, %.19g, %.19g)\n" .. "bad = (%.19g, %.19g, %.19g)", good:getx(), good:gety(), good:getz(), bad:getxyz())
The field
bad.x
turns into garbage.
There are no error messages or warnings.
Similarly, a double whose absolute value is less than 252 253 · 2–63 = 2–64 = .0000000000000000000542101086242752217003726400434970855712890625 becomes zero when copied into a coördinate of a position object. Let’s try that value and the previous double value, which is
253 − 1 253 · 2–64 = 2–64 – 2–117 local good = celestia:newposition(2^-64, 0, 0) local bad = celestia:newposition(2^64 - 2^-117, 0, 0) local s = string.format( "good = (%.45g, %.45g, %.45g)\n" .. "bad = (%.45g, %.45g, %.45g)", good:getx(), good:gety(), good:getz(), bad:getxyz()) good = (5.42101086242752217003726400434970855712890625e-20, 0, 0) bad = (0, 0, 0)
In each case,
the C++ function
celestia_newposition
in
version/src/celestia/celx.cpp
calls the constructor for the C++ class
BigFix
whose argument is a double in
version/src/celutil/bigfix.cpp.
The constructor leaves the position coördinate uninitialized on overflow.
Underflow just goes to zero.
Object:getposition
of a Celestial ObjectWe can get the position of a celestial object at the current simulation time, or at any other time.
--[[
Print the position of the Sun, today and tomorrow.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local sol = celestia:find("Sol")
local today = sol:getposition() --at current simulation time
assert(type(today) == "userdata" and tostring(today) == "[Position]")
local s = string.format("today = (%.15g, %.15g, %.15g)\n",
today:getxyz())
local t = celestia:gettime() + 1
local tomorrow = sol:getposition(t) --at simulation time t
assert(type(tomorrow) == "userdata"
and tostring(tomorrow) == "[Position]")
s = s .. string.format("tomorrow = (%.15g, %.15g, %.15g)",
tomorrow:getxyz())
celestia:print(s, 60)
wait()
end
main()
today = (-0.0175211821017193, -0.000726568584015948, 0.0393328537482719)
tomorrow = (-0.0174232553486754, -0.000728713770735825, 0.0393491020003413)
How many kilometers will the Sun move in the next 24 hours with respect to the universal frame?
local kilometers = today:distanceto(tomorrow) --not microlightyears kilometers = 939.344131605354How many kilometers will MercuryMercury, orbital speed of and VenusVenus, orbital speed of Venus move? What about Halley’s CometHalley’s Comet, orbital speed of at its perihelion on February 9, 1986?
Does JupiterJupiter, effect on Sun of bear the lion’s share of the responsibility for displacing the Sun from the Solar System Barycenter? Find the direction from the barycenter to the Sun, expressed in degrees counterclockwise in the XZ plane from the positive X axis.
local sol = celestia:find("Sol") local position = sol:getposition() local longlat = position:getlonglatPosition:getlonglat()
local s = string.format("%-7s %.15g%s",
sol:name(), math.deg(longlat.longitude), std.char.degree)
Similarly, find the direction from the barycenter to Jupiter. Are the directions approximately 180° apart? Does SaturnSaturn, effect on Sun of make a contribution?
Sol 219.097719310638° Jupiter 56.0906261072159°A body of negligible size responding to the forces of Newtonian physics is called a particleparticle (in Newtonian physics). A particle falling near the surface of the Earth picks up 9.80665 meters per second of velocity during each second that it falls. This gravitational accelerationgravitational acceleration (g) is written with a lowercase gg (gravitational acceleration), and the s2 in the denominator means “per second per second”. g = 9.80665m s2 Therefore after t seconds, the particle is falling at a velocity of V(t) = gt meters per second. Integrating V(t) with respect to t, we find that the distance in meters fallen during the first t seconds is d(t) = 1 2 gt2 For example, the particle covers approximately 4.9 meters during the first second and 19.6 meters during the first two seconds. Another example of finding distance by integration is in Exponential.
Let’s see how well this simple expression d(t) approximates the true distance fallen by the particle. To postpone the moment when the particle hits the ground, we will assume that the mass of the Earth has been crushed into a point at its center. The particle is now free to move from the original surface of the Earth to the center of the Earth along an infinitely narrow, degeneratedegenerate ellipse ellipticalellipse, degenerate orbit—just a straight line.
To create a celestial object named Particle that moves along this orbit,
create a file named
imaginary.ssc
containing the following.
Place it in the
data
subdirectory of the Celx directory
(celxDirectory).
#This file is data/imaginary.ssc.
"Particle" "Sol/Earth"
{
Radius 0
EllipticalOrbit {
Epoch 0 #January 1, 4713 B.C.
Period .0206929593174828 #in Earth days (30 min.)
SemiMajorAxis 3183.725 #in kilometers
Eccentricity .999999999999999 #wish it could be 1
MeanAnomaly 180 #at apogee at time t = 0
}
}
Insert the new filename
"data/imaginary.ssc"
after the existing
"data/solarsys.ssc"
in the list of
SolarSystemCatalogsSolarSystemCatalogs (parameter in celestia.cfg)
in the configuration file
celestia.cfgcelestia.cfg (configuration file),
and restart Celestia.
Where did the above numbers come from?
I wanted the eccentricity to be exactly 1
for a totally degenerate ellipse that is just a straight line.
But this would cause the C++ member function
EllipticalOrbit::positionAtE
in
version/src/celengine/orbit.cpp
to return a position of
(0, 0, 0)
at all times,
so we had to settle for an
almost
degenerate ellipse.
The major axis of the particle’s elliptical orbit
is the radius of the Earth;
the
semi-major axis
is half the radius.
Our value for the
radiusEarth, radius of
was the average of the equatorial and polar radii from the
Earth article
in Wikipedia
(6378.1 and 6356.8 km).
The orbital period
P
in seconds is determined by
Kepler’s
Third
LawKepler’s third law,
where
a
is the semi-major axis in meters,
M
is the
mass of the EarthEarth, mass ofin kilograms
(approximately
5.9736 · 1024,
from the same
Wikipedia article),
and
GG (gravitational constant)
is the
gravitational
constantgravitational constant (G)
(approximately
6.672 · 10–11
m3
kg–1
s–2,
from
version/src/celengine/astro.cpp).
Given these values,
the particle’s orbital period
P
in seconds
works out to approximately 30 minutes.
The standard value of the gravitational acceleration g, 9.80665 meters per second per second, is the sum of a positive term resulting from the force of gravity and a negative term from the Earth’s rotation. The following program ignores the Earth’s rotation, so it removes the negative term from the acceleration. We multiply by 1000 to convert kilometers to meters, and divide by 60 · 60 · 24 to convert seconds to days.
--[[
How many meters does a falling particle travel each second?
]]
require("std")
--variables used by both functions
local earth = celestia:find("Sol/Earth")
local particle = celestia:find("Sol/Earth/Particle")
--Return the distance in kilometers from the center of the Earth
--to the center of the Particle at time t.
local function distance(t)
return earth:getposition(t):distanceto(particle:getposition(t))
end
local function main()
--Keep the Sun in view, but get away from the glare.
local observer = celestia:sane()
observer:setposition(std.position)
local earthRadius = (6378.1 + 6356.8) / 2 --in km, from Wikipedia
local semiMajorAxis = earthRadius / 2
local negativeTerm = -1000 * earthRadius
* (2 * math.pi / (60 * 60 * 24))^2 / math.sqrt(2)
local acceleration = 9.80665 - negativeTerm --in m per s^2
local t0 = 0 --time when particle is at apogee
local s = " t distance .5gt^2 error\n"
for i = 0, 10 do --second by second
local t = t0 + i / (60 * 60 * 24) --i seconds after t0
--distances in meters:
local ellipse = 1000 * math.abs(distance(t) - distance(t0))
local parabola = .5 * acceleration * i^2
s = s .. string.format("%2d %10.6f %10.6f %10.6f\n",
i, ellipse, parabola, math.abs(ellipse - parabola))
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
t distance .5gt^2 error
0 0.000000 0.000000 0.000000
1 4.915106 4.915231 0.000124
2 19.660437 19.660923 0.000486
3 44.236026 44.237076 0.001050
4 78.641975 78.643690 0.001716
5 122.878368 122.880766 0.002398
6 176.945346 176.948303 0.002957
7 240.843072 240.846301 0.003230
8 314.571760 314.574761 0.003001
9 398.131627 398.133682 0.002055
10 491.522937 491.523064 0.000127
For many years astronomers have known that the Milky WayMilky Way, location of center of is shaped like a pancake. But no one knew where its center was, since the plane of the galaxy is full of stars, gas, and dust. It was Harlow ShapleyShapley, Harlow who solved this problem by plotting the positions of the globular clustersglobular clusters and Milky Way above and below the galactic plane. He assumed they formed a spherical halo around the Milky Way, and located the center of the galaxy by locating the center of the halo. See the bibliography.
Let’s try this with Celestia. For now, we will merely compute the average position of the clusters. In alternativeBodyfixed, we will actually see them.
--[[
Print the average of the positions of the globular clusters that surround
the Milky Way.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local sum = std.position0 --(0, 0, 0)
local i = 0
--Assume all globulars belong to the Milky Way.
for dso in celestia:dsos() do
if dso:type() == "globular" then
i = i + 1
sum = sum + dso:getposition()
end
end
if i == 0 then
celestia:print("No globular clusters found.", 10)
wait()
return
end
local average = sum / i
local milkyWay = celestia:find("Milky Way")
local center = milkyWay:getposition()
local kilometersError = center:distanceto(average)
local kilometersRadius = milkyWay:radius()
local s = string.format(
"Actual center = (%.15g, %.15g, %.15g)\n"
.. "Computed center = (%.15g, %.15g, %.15g)\n"
.. "Error = %.15g kiloparsecs = %.15g lightyears\n"
.. "Radius of Milky Way = %.15g kiloparsecs = %.15g lightyears",
center:getx(), center:gety(), center:getz(),
average:getx(), average:gety(), average:getz(),
kilometersError / (1e3 * std.kmPerPc),
kilometersError / (1e6 * KM_PER_MICROLY),
kilometersRadius / (1e3 * std.kmPerPc),
kilometersRadius / (1e6 * KM_PER_MICROLY))
celestia:print(s, 60)
wait()
end
main()
The computed center is only 2 or 3 kiloparsecs from the true center. Not bad, considering that the Milky Way is 30 kiloparsecs in diameter.
Actual center = (-1521500000, -2674310546.875, 27548710937.5) Computed center = (-5755394086.71061, -3381279543.22815, 20043705537.0077) Error = 2.65083051399512 kiloparsecs = 8645.85278389049 lightyears Radius of Milky Way = 15.3300699302482 kiloparsecs = 50000.000786137 lightyears
The position objects share a table of methods called the Lua
metatablemetatable (Lua)
for class
PositionPosition, metatable of.
The division operator in the above expression
sum / i
calls the
__div__div (in metatable)
method (two underscores) in the metatable,
which calls the
__mul__mul (in metatable)
function in the metatable.
These functions were created by the Celx Standard Library
to make it possible to apply the operators
** (position multiplication operator)
and
// (position division operator)
to a position object.
Read the functions in
std.lua
(stdCelx).
Position encoded as string
the 128 Bits of a CoördinateA position contains three coördinates, each in the 128-bit format we saw in positionCoordinates. These 128 bits consist of 16 bytes of 8 bits each. The bytes are numbered from 0 to 15 (least to most significant). The bits within each byte are numbered from 0 to 7 (least to most significant).
The value of the coördinate is a binary number with 64 bits to the left of the binary point and 64 bits to the right. Bytes 8 through 15 are the integer, bytes 0 though 7 are the fraction, and the binary point is fixed in the middle.
Unfortunately,
these 128-bit values are far too wide to fit into the arguments of
Celestia:newposition
or the return values of
Position:getx,
gety,
and
getz.
A Celx number can hold only 64 bits;
see
doubleArithmetic.
But a Celx program can read and write the 128-bit values indirectly.
Instead of passing three numbers to
Celestia:newpositioncelestia:newposition,
we can pass it three strings.
Each character in the strings represents six bits,
and the entire string represents 128 bits.
The following characters are used.
"A" represents 000000 (0)
"B" represents 000001 (1)
"Z" represents 011001 (25)"a" represents 011010 (26)
"b" represents 011011 (27)
"z" represents 110011 (51)"0" represents 110100 (52)
"1" represents 110101 (53)
"9" represents 111101 (61)"+" represents 111110 (62)
"/" represents 111111 (63)
Each string passed to
Celestia:newposition
starts with the least significant byte and ends with the most significant.
Within each byte,
we start with the most significant bit
and end with the least significant.
Thus a string begins with the most significant bit
of the least significant byte.
The empty string represents zero.
Blanks are ignored and can be used for legibility.
The three strings in the following program represent the coördinates
(–1, 0, 1).
In the string representing 1,
the first ten
A’s
represent 60 of the 64 bits of the fraction:
bytes 0 through 6 inclusive,
and the four most significant bits of byte 7.
The eleventh
A
straddles the four least significant bits of byte 7
and the two most significant bits of byte 8.
The
B,
representing
000001,
is the six least significant bits of byte 8.
The remaining 56 bits default to zeroes.
The value
–1
is represented by
a fraction of 64 zeroes in bytes 0 through 7,
and an integer of 64 ones in bytes 8 through 15.
As before, the ten
A’s
represent bytes 0 through 6 inclusive,
and the four most significant bits of byte 7.
The
D,
representing
000011,
straddles the four least significant bits of byte 7
and the two most significant bits of byte 8.
The ten slashes represent the middle 60 bits of the integer, all ones.
The lowercase
w,
representing
110000,
is the two least significant bits of byte 15,
followed by four unused bits.
--[[
Create a position from three strings.
]]
require("std")
local function main()
--The Sun will be out of the window to the observer's right.
local position = celestia:newposition(
"AAAA AAAA AAD/ //// //// /w", --represents -1
"", --represents 0
"AAAA AAAA AAAB") --represents 1
assert(type(position) == "userdata"
and tostring(position) == "[Position]")
local observer = celestia:sane()
observer:setposition(position)
local s = string.format("(%.15g, %.15g, %.15g)", position:getxyz())
celestia:print(s, std.duration)
wait()
end
main()
(-1, 0, 1)
An easier way to compose the three strings is with the function
std.tourlstd.tourl.
It accepts three string arguments
that look like plain old decimal numbers,
each with an optional minus sign and optional decimal point but no exponent.
It returns three strings that encode the numbers in the format passed to
Celestia:newposition.
Did it work?
The standard library methods
Position:getbinaryPosition:getbinary,
getdecimalPosition:getdecimal,
and
gethexPosition:gethex
return tables of strings spelling out the coördinates in
bases 2, 10, and 16 respectively.
Also,
the method
Position:geturlPosition:geturl
is the converse of
std.tourl.
It returns a table of strings that could be passed to
Celestia:newposition.
This format could also be used in a Celestia
cel:
URL.
--[[
Write and read all 128 bits of the coordinate values of a position.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
local x, y, z = std.tourl(
"1234567890123456789.1234567890123456789",
"1",
"-1")
local s = string.format(
"String encoding:\n"
.. "(\"%s\", \"%s\", \"%s\")\n\n",
x, y, z)
local position = celestia:newposition(x, y, z)
s = s .. string.format(
"64-bit double values:\n"
.. "(%.15g, %.15g, %.15g)\n\n",
position:getxyz())
local hex = position:gethex()
s = s .. string.format(
"128-bit values in hexadecimal:\n"
.. "x = %s\n"
.. "y = %s\n"
.. "z = %s\n\n",
hex.x, hex.y, hex.z)
local decimal = position:getdecimal()
s = s .. string.format(
"128-bit values in decimal:\n"
.. "x = %s\n"
.. "y = %s\n"
.. "z = %s\n\n",
decimal.x, decimal.y, decimal.z)
local url = position:geturl()
s = s .. string.format(
"Back to strings:\n"
.. "(\"%s\", \"%s\", \"%s\")",
url.x, url.y, url.z)
celestia:print(s, math.huge, -1, 1, 1, -1) --upper left
wait()
end
main()
The value 1234567890123456789.1234567890123456789 is a repeating fraction in binary, like ⅓ in decimal. It therefore cannot be stored in a finite number of bits. But the value that we have stored in the x coördinate is as close as we can get to it with the 128 bits at our disposal. Rounded to the nearest 10–19, it would give us the desired value exactly.
String encoding: ("HF/2Rjfdmh8Vgel99BAiEQ", "AAAAAAAAAAAB", "AAAAAAAAAAD//////////w") 64-bit double values: (1.23456789012346e+18, 1, -1) 128-bit values in hexadecimal: x = 112210F47DE981151F9ADD3746F65F1C y = 00000000000000010000000000000000 z = FFFFFFFFFFFFFFFF0000000000000000 128-bit values in decimal: x = 1234567890123456789.12345678901234567888776927357952217789716087281703948974609375 y = 1 z = -1 Back to strings: ("HF/2Rjfdmh8Vgel99BAiEQ", "AAAAAAAAAAAB", "AAAAAAAAAAD//////////w")
Look at the method
Position:getbinary
in
std.lua
(stdCelx)
and see how it reads the 128 bits of a coördinate.
But first,
we must understand how a negative number is stored in the fixed point format.
Most machines would use the
two’s
complement
representationtwo’s complement format,
modeled on an odometer running backwards:
In binary, the moral equivalent of 9999 is 1111:
0011The most significant bit of a coördinate—the one on the far left—is the most significant bit of byte 15. It is 1 for a negative number, 0 for a nonnegative, and is therefore called the sign bitsign bit (two’s complement). We can get the value of the sign bit simply by testing whether the number is negative or nonnegative.
How can we examine the other 127 bits?
We have seen that we can add two positions together
to get a new position
(averagePosition).
In particular,
we can add a position to itself,
thus doubling the value of each coördinate.
Doubling a binary number shifts all of its bits one place to the left,
and repeated doublings cause repeated shifts.
One by one, each of the 128 bits can be shifted into the
position of the sign bit,
where its value can be examined.
For another example of shifting,
see the implementation of the function
std.utf8.
Verify that all but 15 significant decimal digits are
lostprecision, loss of
when multiplying a position by a Celx number.
This is because the
__mul
function in the
Position
metatable is implemented in Celx,
causing its argument to be a 64-bit Celx number.
--Move twice as far away from the Solar System Barycenter.
position = 2 * position
The following code will perform the operation
without any loss of precision.
This is because the
__add__add (in metatable)
function in the
Position
metatable is implemented in C++,
allowing its argument to be a 128-bit fixed point number.
--Move twice as far away from the Solar System Barycenter.
position = position + position
Vector (class)
A
vector
object holds the distance and direction between two positions.
Think of it as an arrow pointing from one position to the other.
Like a position, a vector has
the fields
x,
y,
z
and the methods
getxVector:getx,
getyVector:gety,
getzVector:getz,
and
getxyzVector:getxyz,
but the values are plain, ordinary doubles
(doubleArithmetic).
The unit of distance is the microlightyear
(linearDistance).
The following program shows three ways to create the same vector.
Each one is an arrow pointing from the
source
position (the Sun) to the
destination
position (the Earth).
Since the Sun and Earth are in constant motion,
we must get their positions at the same simulation time.
It’s easy
to accomplish this:
just make no call to
waitwait
between the two calls to
Object:getpositionObject:getposition.
The method
Vector:normalizeVector:normalize
returns a
unit
vectorunit vector—one
whose length is 1—pointing in the same direction as the original vector.
Only a vector of positive length can be
normalizednormalize a vector,
on pain of
division by zero.
But see the fine print in the exercises below.
--[[
Create three vectors, measure their lengths, and normalize them.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local source = sol:getposition()
local destination = earth:getposition()
--Three ways to create the same vector,
--pointing from source to destination.
local v1 = celestia:newvector(
destination:getx() - source:getx(),
destination:gety() - source:gety(),
destination:getz() - source:getz())
local v2 = destination - source
local v3 = source:vectortoPosition:vectorto(destination)
local s = string.format(
"v1 = (%.15g, %.15g, %.15g)\n"
.. "v2 = (%.15g, %.15g, %.15g)\n"
.. "v3 = (%.15g, %.15g, %.15g)\n\n"
.. "v1:length() = %.15g",
v1:getx(), v1:gety(), v1:getz(),
v2:getx(), v2:gety(), v2:getz(),
v3:getx(), v3:gety(), v3:getz(),
v1:lengthVector:length())
if v1:length() > 0 then
local v4 = v1:normalize()
s = s .. string.format(
"\n"
.. "v4 = (%.15g, %.15g, %.15g)\n"
.. "v4:length() = %.15g",
v4:getx(), v4:gety(), v4:getz(),
v4:length())
end
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
v1 = (-11.2082594771348, -0.000301974087853152, -10.8365831649699)
v2 = (-11.2082594771348, -0.000301974087853152, -10.8365831649699)
v3 = (-11.2082594771348, -0.000301974087853152, -10.8365831649699)
v1:length() = 15.5902730986112
v4 = (-0.718926436133647, -1.93693905131175e-05, -0.695086166639072)
v4:length() = 1
The above distances are in microlightyears.
The distance returned by the following method
Position:distancetoPosition:distanceto
is in kilometers.
--[[
Get the distance between the Sun and Earth in microlightyears, kilometers,
and astronomical units.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local sol = celestia:find("Sol"):getposition()
local earth = celestia:find("Sol/Earth"):getposition()
local microlightyears = (sol - earth):length()
local kilometers = sol:distanceto(earth)
local s = string.format(
"Current distance from Sun to Earth:\n"
.. "%.15g microlightyears\n"
.. "%.15g kilometers\n"
.. "%.15g astronomical units",
microlightyears,
kilometers,
microlightyears / std.microlyPerAu)
celestia:print(s, 60)
wait()
end
main()
Current distance from Sun to Earth:
15.5902730986112 microlightyears
147495371.779888 kilometers
0.985945662794036 astronomical units
If we try to normalize a vector of length zero,
Celestia will divide by zero.
The road to ruin starts at the Celx method
Vector:normalize,
which calls the C++ function
vector_normalize
in
version/src/celestia/celx_vector.cpp,
which calls the C++ member function
Vector3<T>::normalize
in
version/src/celmath/vecmath.h,
which performs the fatal division.
The C++ Standard says “the behavior is undefined”
when dividing by zero,
which means anything can happen.
My machine gave me a vector of three
“not a numbers”not a number (nan).
It seems to be taunting me:
What happens on your machine?
Microsoft Windows prints “not a number”
as the indeterminate symbol
-1.#IND.
Even if a vector has one or more nonzero coördinates,
the methods
Vector:length
and
Vector:normalize
might still think its length is zero.
This is because the length of a vector
v
is computed as follows.
Assuming our doubles have the standard 53-bit mantissa, the smallest positive double is the following denormalized value (denormalized).
1 253 · 2–1021 = 2–1074 ≈ 4.94065645841247 · 10–324A small number gets even smaller when squared. The smallest positive double whose square is nonzero is
2 · 2–538 ≈ 6,369,051,672,525,773 253 · 2–537Its square is 2–1075, which is rounded up to 2–1074.
local x = math.sqrt(2) * 2^-538 --its square is smallest positive double local y = x - (1 / 2^53) * 2^-537 --the previous double value --local y = std.prevstd.prev(x) --easier way to get the same value
local s = string.format(
"x = %.17g, x * x = %.15g\n"
.. "y = %.17g, y * y = %.15g",
x, x * x,
y, y * y)
x = 1.5717277847026288e-162, x * x = 4.94065645841247e-324
y = 1.5717277847026285e-162, y * y = 0
So a vector all of whose coördinates have an absolute value less than
2
·
2–538
will have a computed length of zero,
causing
Vector:normalize
to behave unpredictably.
Let’s get an upright view of the constellation CygnusCygnus the Swan, a.k.a. the Northern CrossNorthern Cross (Cygnus). The observer will look towards the star SadrSadr (star) (γ Cygni, the chest of the swan). At the top of the picture will be DenebDeneb (star) (α, the tail); at the bottom, AlbireoAlbireo (β, the head).
The observer will be oriented with
Observer:lookatObserver:lookat.
Its next-to-last argument is the
target position
to look at,
always in universal coördinates.
The vector from the observer’s position
to the target position will be the observer’s
forward vectorforward vector of orientation,
pointing in the direction in which he will look.
The last argument of
Observer:lookat
is the
up vectorup vector of orientation,
also in universal coördinates.
It points towards the observer’s zenith,
the direction he thinks is up.
With our up vector of
deneb:getposition() - albireo:getposition(),
the observer will be oriented so that
Deneb appears directly above Albireo.
The forward and up vectors are supposed to be perpendicular.
If they are not,
the forward vector takes precedence
and the up vector is adjusted to accommodate it.
The new up vector is exactly perpendicular to the forward vector,
and lies in the plane of the forward vector and the original up vector.
It is always less than
90°
from the original up vector.
We say that the up vector has been
erectederect a vector;
see
Vector:erect
in
erect.
Observer:lookat
has an optional third-from-last argument;
see
parallax.
If you prefer the
LatinLatin language
genitive
casegenitive case (Latin)
to the
ArabicArabic language
nominativenominative case (Arabic),
you can specify the stars by their
Bayer
designationsBayer designation (of star):
"Alpha Cygni",
"Alpha Cyg",
or even
std.char.alpha .. " Cyg".
To highlight the constellation,
we double the
Renderer::ConstellationColorRenderer::ConstellationColor (C++ constant)
in
version/src/celengine/render.cpp.
--[[
Look at Cygnus the Swan, positioning Deneb above Albireo.
The Albireo-to-Deneb vector points straight up.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:show("boundaries") --constellation boundaries
observer:setfov(math.rad(46)) --wide enough to see whole constellation
celestia:setconstellationcolor(2 * 0, 2 * .24, 2 * .36, {"Cygnus"})
local deneb = celestia:find("Deneb") --Alpha, tail of swan
local sadr = celestia:find("Sadr") --Gamma, chest
local albireo = celestia:find("Albireo") --Beta, head
local up = deneb:getposition() - albireo:getposition() --up is a vector
observer:lookat(sadr:getposition(), up)
wait()
end
main()
To flip the observer upside down, we could use the opposite up vector. Here are two ways to negate it:
local up = albireo:getposition() - deneb:getposition() observer:lookat(sadr:getposition(), up) local up = deneb:getposition() - albireo:getposition() observer:lookat(sadr:getposition(), -up) --unary minus
For the fun-loving programmer,
Observer:lookat
offers four ways of
dividing by zerodivision by zero.
In each case,
the division is attempted when
the C++ function
observer_lookat
in
version/src/celestia/celx_observer.cpp
calls the C++ member function
Vector3<T>::normalize
in
version/src/celmath/vecmath.h.
On my machine, the Universe went black.
What happens on yours?
A position and a vector contain the same Cartesian coördinates, so the standard library provides conversion functions.
local earth = celestia:find("Sol/Earth") local position = earth:getposition() --Convert the position to a vector pointing --from the origin (the Solar System Barycenter) to the Earth. local vector = position:tovectorPosition:tovector()
--Convert the vector back to the Earth's position.
position = vector:topositionVector:toposition()
Conversion from position to vector will usually
lose precisionprecision, loss of
because a coördinate occupies 128 bits in a position
but only 64 in a vector.
The method
Position:tovector
accepts this loss as a fact of life and does not warn about it.
On the other hand,
the method
Vector:toposition
calls the Lua function
errorerror (Lua function)
if the absolute value of a vector coördinate is greater than or equal to
263.
In this case,
the conversion would have resulted in garbage
(observerSetposition).
If a program does not
require
the Celx Standard Library,
positions and vectors will be handled very differently.
If the program does use the library,
positions and vectors will be more interchangeable
and there will be fewer reasons to call the conversion methods.
The following are the major examples.
Rotation:transformRotation:transform
(transformVector)
will accept a vector argument.
With the library, it will also accept a position.Frame:fromFrame:from
and
Frame:toFrame:to
(eclipticFrame)
will accept a position argument.
With the library, they will also accept a vector.
But even with the library,
there will still be some differences between positions and vectors.
The methods
Observer:lookat
(direction)
and
Position:orientationto
(convertForward)
accept only a position as their first argument,
and only a vector as their second.
The dot product
(dotProduct)
and cross product
(crossProduct)
operations can be performed only on vectors.
The sum of a position and a vector is always a position,
and the difference of two positions or of two vectors is always a vector.
Verify that
Vector:toposition
warns about overflow but not underflow.
Verify that
Position:tovector
usually results in loss of precision.
After converting the position to a vector and back again, the x coördinate lost the last two decimal digits of its integral part and the y coördinate lost the last two decimal digits of its fractional part. The z coördinate lost the last two decimal digits of its integer and all of its fraction.
1234567890123456789 0.12345678901234567888776927357952217789716087281703948974609375 1234567890123456789.12345678901234567888776927357952217789716087281703948974609375 1.23456789012346e+18 0.123456789012346 1.23456789012346e+18 1234567890123456768 0.12345678901234567736988623209981597028672695159912109375 1234567890123456768
The
dot product
of two vectors
v
and
w
is a number from which we can extract the
angleangle between vectors
between the vectors.
The dot product is written as
v *
in Celx and as
v · w
in mathematics.
(The raised dot character is
* (dot product operator) wstd.char.middotstd.char.middot.)
The value of the dot product is
v · w =
||v||
||w||
coscosine (trig function) θ
where
||v||
and
||w||
are the lengths of the vectors
(distancePositions),
and
θ
is the angle between the vectors.
(The Greek letter theta is
std.char.theta.)
The dot product operation is
commutativecommutativity of dot product
and
associativeassociativity of dot product
because multiplication is commutative and associative.
Its value is zero if the vectors are perpendicular,
because
cos 90° = 0.
It is also zero if either vector is of length zero.
If both vectors are of positive length, there is a meaningful angle θ between them. We can solve for the cosine of this angle, cos θ = v · w ||v|| ||w|| and then for the angle itself. Arccosarccosine (trig function) means “the angle whose cosine is”. θ = arccos v · w ||v|| ||w||
In Celx we could compute the angle as follows. The first asterisk is a plain old multiplication of two numbers; the second asterisk is a dot product of two vectors.
--[[ v and w must be nonzero vectors. theta is the angle between them in radians, in the range 0 to pi inclusive. ]] local product = v:length() * w:length() assert(product > 0) local theta = math.acosmath.acos(v * w / product)
We can write this more simply with the standard library method
Vector:angleVector:angle,
analogous to
Position:distanceto.
It calls the Lua function
errorerror (Lua function)
if either vector is of length zero.
--[[
v and w must be nonzero vectors.
theta is the angle between them in radians,
in the range 0 to pi inclusive.
]]
local theta = v:angle(w)
--Same value: the order doesn't matter.
--local theta = w:angle(v)
Warning:
math.acos
and
Vector:angle
return an angle in the range 0 to
π
radians inclusive.
If we need an angle in a bigger range such as 0 to
2π,
or
–π
to
π,
we’ll have to compute it ourselves with
math.atan2math.atan2.
The most straightforward examples are in
Position:getlonglatPosition:getlonglat
and
Vector:getlonglatVector:getlonglat.
According to an old chestnut of astronomy,
the
pointersPointers (of Big Dipper)
of the
Big DipperBig Dipper
are five degrees apart.
Let’s see if it’s true.
Their names are
DubheDubhe (star)
and
MerakMerak (star),
a.k.a.
"Alpha"
and
"Beta Ursae Majoris".
We’ll face towards
Megrez
("Delta",
the star that joins the handle to the bowl),
with the north pole of the ecliptic towards the top of the window.
--[[
Look at the Big Dipper, with Draco overhead. Print the angular distance
between the pointers, as seen from the Solar System Barycenter.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position) --Avoid Sol's glare.
celestia:setconstellationcolor(2 * 0, 2 * .24, 2 * .36, {"Ursa Major"})
--Dubhe and Merak are the pointers of the Big Dipper.
local dubhe = celestia:find("Dubhe") --Alpha Ursae Majoris
local merak = celestia:find("Merak") --Beta
local megrez = celestia:find("Megrez") --Delta, joins bowl to handle
dubhe:mark()
merak:mark()
--The Y axis of the universal frame points from the Solar System
--Barycenter towards the north pole of the ecliptic in Draco.
observer:lookat(megrez:getposition(), std.yaxis)
--The vectors toDubhe and toMerak point from the Solar System Barycenter
--to Dubhe and Merak.
local toDubhe = dubhe:getposition():tovector()
local toMerak = merak:getposition():tovector()
local theta = toDubhe:angle(toMerak) --in radians
local az = std.toaz(theta) --convert to degrees, minutes, seconds
local s = string.format(
"Seen from our Solar System,\n"
.. "the pointers of the Big Dipper "
.. "are %d%s %d%s %.15g%s apart.",
az.degrees, std.char.degree,
az.minutes, std.char.minute,
az.seconds, std.char.second)
celestia:print(s, 60)
wait()
end
main()
Seen from our Solar System,
the pointers of the Big Dipper are 5° 22′ 27.2320068968585″ apart.
The Winter TriangleWinter Triangle consists of the stars SiriusSirius (star), ProcyonProcyon (star), and BetelgeuseBetelgeuse (star). How equilateral is it? Measure the apparent angular distance between Sirius and Procyon, Procyon and Betelgeuse, etc. What about the Great SquareGreat Square of Pegasus of PegasusPegasus?
How high above the horizon is the Sun
at 17:00 UTC (Noon in Eastern Standard Time) on January 1, 2014
as seen from
"Sol/Earth/Washington D.C."?
(One space, no comma, two periods.)
Or instead of Washington,
you can add your own city to Celestia’s
data/world-capitals.ssc
file,
giving it an appropriate level of
Importance.
Then restart Celestia.
Create a vector from the center of the Earth to Washington, and a vector from Washington to the center of the Sun. The angle θ between the vectors is the Sun’s angular distance down from Washington’s zenithzenith. The complementary anglecomplementary angles 90° − θ is the Sun’s angular distance up from Washington’s horizon. (Be careful not to mix radians with degrees.) The Sun should be about 28° up from the horizon.
Is the Sun lower in the sky an hour later? By trial and error, find the time when the center of the sun sets. Better yet, find when the upper limb (edge) of the Sun sets. In whenSunset, the Celx program will do the trial and error automatically. And in altazimuthCoordinates, we’ll have an easier way to measure the angles.
How high above the lunar horizon was the Sun
at 20:17:40 UTC on
July 20, 1969Apollo 11
as seen from
"Sol/Earth/Moon/Mare Tranquillitatis"Mare Tranquillitatis (lunar sea)?
(One space after the
Mare;
it’s pronounced “mah-ray”.)
The answer should be about
19°.
EagleApollo Lunar Module,
you are Stay for T1.
Seen from the Earth, MercuryMercury, elongation of is usually lost in the glare of the Sun. The planet is easiest to see when it is at the greatest elongationelongation (of Mercury) (angular distance) from the Sun. What is Mercury’s elongation on September 21, 2014 at 18:00 UT? Create vectors from the Earth to the Sun, and from the Earth to Mercury. The answer should be about 26°.
local earth = celestia:find("Sol/Earth") local mercury = celestia:find("Sol/Mercury") --vector from Earth to Mercury local toMercury = mercury:getposition() - earth:getposition()Print a table showing the angular distance between the Sun and Mercury at 18:00 UTC on each day from September 18 to September 24, 2014 inclusive. On which day does Mercury reach its greatest elongation? To zero in on the exact time, see mercuryPerihelion.
local mercury = celestia:find("Sol/Mercury") --first and last are whole numbers because of the 12s. local first = celestia:tojulianday(2014, 9, 18, 12) local last = celestia:tojulianday(2014, 9, 24, 12) for day = first, last do local utc = celestia:fromjulianday(day) local t = celestia:utctotdb(utc.year, utc.month, utc.day, 18) local mercuryPosition = mercury:getposition(t) --etc. endThe cosmic microwave background radiationcosmic microwave background radiation comes at us from every direction. The Earth ploughs through this radiation at several hundred kilometers per second, heading in the direction of RA 11h 11m 57s Dec –7.22° in the constellation LeoLeo. The Doppler effectDoppler effect causes the radiation coming from Leo to seem hotter, and that from Aquarius, on the other side of the sky, to seem colder.
Let’s paint the whole sky to show the different temperatures.
The vector
toHot
points towards the hot spot in Leo,
and
toStar
points towards each star in the sky.
The angle between them determines the color with which we mark the star.
See
rotatedRadec
for the
radecFrame.
Normally a program is interrupted if it does not call
waitwait
at least once every five seconds.
Our loop will take much longer than this,
so we lengthen the interval with
Celestia:settimesliceCelestia:settimeslice.
--[[
Color the sky to show the dipole in the Cosmic Microwave Background: hot violet
around our destination in Leo, cold red in Aquarius on the other side of the
sky. Drag on the sky or press the arrow keys.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position0)
observer:setfov(observer:getfov() * 4 / 3) --see entire violet circle
--[[
The Earth is moving towards RA 11h 11m 57s Dec -7.22 degrees in Leo.
The radiation looks hotter there.
It's moving away from the point on the other side of the sky.
]]
local toCold = celestia:newvectorradec(
math.rad((23 + (11 + 57 / 60) / 60) * 360 / 24),
math.rad(7.22))
local radecFrame = celestia:newframe("universal", std.radecRotation)
observer:lookat(
observer:getposition() - toCold, --Look away from the cold spot,
radecFrame:from(std.yaxis)) --with Polaris towards top.
--Indigo is weak.
local color =
{"red", "orange", "yellow", "green", "blue", "indigo", "violet"}
local seconds = 30 --of real time; may have to make it even longer
local s = string.format("Painting the sky will take about %d seconds.",
seconds)
celestia:print(s, 5)
wait(5)
celestia:settimeslice(seconds)
local t0 = celestia:getscripttime()
for star in celestia:stars() do
local toStar = star:getposition():tovector()
if toStar:length() > 0 then --don't let angle divide by zero
local theta = toCold:angle(toStar) --from star to Aquari
--Convert theta to int in range 1 to #color inclusive.
local c = math.ceil(#color * theta / math.pi)
star:mark(color[c], "diamond", 10, .25) --size and alpha
end
end
--Don't drag on sky until it is completely painted.
s = string.format("Painting the sky took %.15g seconds.",
celestia:getscripttime() - t0)
celestia:print(s, 60)
wait()
end
main()
Experiment with a more impressionistic way of painting the sky.
--misty, overlapping disks star:mark(color[c], "disk", 100, .008)The annual parallaxparallax of a star is the change in its apparent position, as seen from the Earth, caused by the Earth’s revolution around the Sun. Let’s measure the annual parallax of the nearest star, Proxima CentauriProxima Centauri (star). The Proxima system is easy to work with because Celestia considers it to be a single star, disregarding its tenuous connection with Alpha CentauriAlpha Centauri (star).
As in
direction,
the next-to-last argument of
Observer:lookatObserver:lookat
is the target position.
The last argument is the up vector.
The rarely seen third-from-last argument of
Observer:lookat
is the
source position.
If the source position is absent,
the observer looks directly at the target position.
If the source position is present,
he looks along a vector
parallel to the one from the source position to the target position.
When the following
lookats
are executed,
six months apart,
the observer will therefore look along parallel vectors.
This will keep the background sky immobile as Proxima blinks back and forth.
Proxima blinks along a line parallel to the ecliptic.
We therefore display the ecliptic grid instead of the equatorial,
and our up vector is
std.yaxis.
It points towards the north pole of the
ecliptic
in
Draco,
making the ecliptic horizontal.
We make the Earth invisible so that the observer,
at its center, can see out of it.
The
toProxima
vectors go from the center of the Earth to Proxima.
As usual, the vectors are in microlightyears.
Celestia knows most stellar distances to only at most 10 significant digits
(see
version/data/stars.txt),
so the distance read from the database is formatted with
"%.10g".
--[[
Blink Proxima Centauri back and forth due to is annual parallax.
Watch the date change in the upper right corner.
]]
require("std")
local function main()
local observer = celestia:sane()
--Minimum field of view, for maximum magnification.
observer:setfov(.001) --.001 radians = approx. 26 seconds of arc.
--Set up for astrometry. With automagautomag (renderflag) off,
--setfaintestvisible can go all the way down to the 15th magnitude.
celestia:hide("automag", "galaxies", "grid")
celestia:show("eclipticgrid")
celestia:setfaintestvisibleCelestia:setfaintestvisible(15)
celestia:setstarstyleCelestia:setstarstyle("point") --default is "fuzzy"
celestia:settimescale(0) --freeze the passage of time
local earth = celestia:find("Sol/Earth")
local proxima = celestia:find("Proxima Centauri")
--Make sure we can see the universe from the center of the Earth.
earth:setvisibleObject:setvisible(false)
--a is an array with two values, a[1] and a[2]. Each value will be
--a table with four fields: time, earth, proxima, toProxima.
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
local a = {
{time = celestia:utctotdb(year, 2, 17)},
{time = celestia:utctotdb(year, 8, 22)}
}
for i = 1, #a do
a[i].earth = earth:getposition(a[i].time)
a[i].proxima = proxima:getposition(a[i].time)
a[i].toProxima = a[i].proxima - a[i].earth
end
local theta = a[1].toProxima:angle(a[2].toProxima)
local radians = theta / 2 --parallax in radians
local seconds = 60 * 60 * math.deg(radians) --parallax in seconds of arc
local baseline = (a[2].earth - a[1].earth):length() / 2 --orbit radius
local parallaxDistance = baseline / math.sin(radians)
local measuredDistance =
(a[1].toProxima:length() + a[2].toProxima:length()) / 2
local s = string.format(
"Parallax %.15g%s yields a distance of %.15g parsecs\n"
.. "or %.15g lightyears.\n"
.. "Distance read from database is %.10g lightyears.",
seconds, std.char.second,
1 / seconds, --convert parallax to parsecs
parallaxDistance / 1e6, --convert microlightyears to lightyears
measuredDistance / 1e6)
celestia:print(s, 60)
while true do --infinite loop
for i = 1, #a do
celestia:settime(a[i].time)
observer:setposition(a[i].earth)
observer:lookat(std.position0, a[i].proxima, std.yaxis)
wait(1) --Freeze the picture for one second.
end
end
end
main()
Parallax 0.768987719149221″ yields a distance of 1.30041088446297 parsecs
or 4.24218988334848 lightyears.
Distance read from database is 4.24200022 lightyears.
Remove the third-from-last argument of
Observer:lookat.
Note that Proxima now remains immobile,
while the background sky (i.e., the ecliptic grid) blinks back and forth.
How did we pick the dates when Proxima would be the farthest to the left and right? Construct a vector from the Sun to the Earth, and a vector from the Sun to Proxima Centauri. Display the angle in degrees between the vectors. By trial and error, find the two dates when the angle is 90°. We’ll be able to do this automatically in findZero.
Celestia knows about the orbits of individual stars within a star system, but not about the motion of the system through the galaxy. We therefore made no attempt to measure the secular parallaxsecular parallax of Proxima, caused by the motion of the Sun and Proxima through the galaxy over the course of many years.
The greatest secular parallax is exhibited by Barnard’s StarBarnard’s Star. Demonstrate conclusively that Celestia thinks the stars are fixed by displaying two views of this star, ten years apart.
Simulate Clyde TombaughTombaugh, Clyde’s famous pair of discovery photos of PlutoPluto, discovery of, January 23 and 29, 1930. Blink back and forth between them.
Does the Sun have planets? Could an extraterrestrial astronomer at a nearby star see the Sun’s wobble around the Solar System Barycenter? Could he, she, it, or they deduce the existence of JupiterJupiter, effect on Sun of?
The
cross product
of two vectors
v
and
w
is a vector perpendicular to both of them.
The cross product is written as
v ^
in Celx
and as
v × w
in mathematics.
(The cross is
^ (cross product operator) wstd.char.crossstd.char.cross,
and the
caretcaret (cross product operator)
is half of a cross.)
The unit vectors
right
and
up
in the following program point right and up.
Their cross product
towardsUs
is a unit vector pointing towards us.
It is perpendicular to
right
and
up because it is the result of a cross product operation.
It points towards us rather than away from us because of the following
right-hand
ruleright-hand rule for cross product.
Make a “thumbs up” fist with your right hand and grasp
towardsUs
in your four non-thumb fingers,
keeping the following requirements satisfied.
right)
towards the right operand
(the vector up).Given our three vectors, there’s only one way to satisfy both requirements. Your fist will be in front of you, knuckles up, with your thumb aimed at your eye. The right-hand rule says that your thumb is now pointing in the direction of the cross product. The cross product operation is not commutativecommutativity, cross product lacking in: if we swap the two operands, the resulting vector will have its direction reversed. The cross product is not associativeassociativity, cross product lacking in either.
The length of the cross product is ||v × w|| = ||v|| ||w|| sin θ where θ is the angle between v and w. The length is zero if the vectors are colinearcolinear vectors, pointing in the same or in opposite directions, because sin 0° = sin 180° = 0. The length is also zero if either vector is of length zero.
The length of the cross product can be visualized as the area of the parallelogram spanned by v and w. It is zero when θ = 0° or 180°, and greatest when θ = 90° and the parallelogram is a rectangle. The parallelogram in the following program is a unit square, so the cross product is of length 1.
Do not try to compute the angle between the vectors by solving the above formula for θ. The angles of 45° and 135°, for example, have the same sine (1/2), and the cross product gives no clue as to which of these angles is θ. To get the angle, use the dot product in dotProduct.
--[[
Compute the cross product of two perpendicular unit vectors.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local right = celestia:newvector(1, 0, 0)
local up = celestia:newvector(0, 1, 0)
local towardsUs = right ^ up --cross product is (0, 0, 1)
local s = string.format(
"(%.15g, %.15g, %.15g) %s "
.. "(%.15g, %.15g, %.15g) = "
.. "(%.15g, %.15g, %.15g)\n"
.. "%s = %.15g%s\n",
right:getx(), right:gety(), right:getz(),
std.char.cross,
up:getx(), up:gety(), up:getz(),
towardsUs:getx(), towardsUs:gety(), towardsUs:getz(),
std.char.theta, math.deg(right:angle(up)), std.char.degree)
celestia:print(s, 60)
wait()
end
main()
(1, 0, 0) × (0, 1, 0) = (0, 0, 1)
θ = 90°
The cross product will be used to find the line common to two intersecting planes. Elegant examples are in Sundial, which draws the lines on the face of a sundial, and recoverElliptical, which constructs a vector pointing towards the “ascending node” of an orbit.
We made
Cygnus
vertical in
direction.
Now let’s make
Orion’s Belt
horizontal.
From left to right its three stars are
AlnitakAlnitak (star)
("Zeta Orionis"),
AlnilamAlnilam (star)
("Epsilon"),
and
MintakaMintaka (star)
("Delta").
The vector
mintaka:getposition() - p
points from the observer to Mintaka,
and the vector
alnitak:getposition() - p
from the observer to Alnitak.
Their cross product,
up,
is a vector perpendicular to the first two.
It points north rather than south because of the above right-hand rule.
With
up
pointing up,
the belt is horizontal.
--[[
Look at Orion's Belt.
Orient the observer so that the belt is horizontal, with north at the top.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setfov(math.rad(5))
celestia:show("boundaries")
celestia:setconstellationcolor(0, 2 * .24, 2 * .36, {"Orion"})
local p = std.position --Avoid Sol's glare.
observer:setposition(p)
--The stars of the belt, left to right:
local alnitak = celestia:find("Alnitak") --Zeta Orionis
local alnilam = celestia:find("Alnilam") --Epsilon
local mintaka = celestia:find("Mintaka") --Delta
local up = (mintaka:getposition() - p) ^ (alnitak:getposition() - p)
observer:lookat(alnilam:getposition(), up)
wait()
end
main()
After launching the above program,
zoom
out by pressing
.. (zoom out command)
(period)
to verify that the belt points left to
Sirius,
right to
Aldebaran.
Then automate the zoom by adding the following code.
Hide the grid while the zoom is in progress
because it distracts the user when the grid lines disappear as we pull back.
As we zoom out,
the fraction
(t - t0) / (t1 - t0)
goes from 0 to 1.
The variable
fov
therefore goes from
fov0
to
fov1.
After you read gradualStart, change the local fov = fov0 + (fov1 - fov0) * (t - t0) / (t1 - t0) in the above fragment to local fov = std.spline(t, t0, t1, fov0, fov1)
How straight is Orion’s belt? Consider the plane containing Mintaka, the Sun, and Alnilam, and use a cross product to construct a vector perpendicular to this plane. Do the same for the plane containing Alnilam, the Sun, and Alnitak. The angle between the vectors should be about 7.5°, so the belt is 7.5° from having a straight angle of 180° at Alnilam.
How equiangular is the Winter TriangleWinter Triangle of SiriusSirius (star), ProcyonProcyon (star), and BetelgeuseBetelgeuse (star)? Is the sum of its angles greater than 180°?
Let’s watch Venus going through her phases as seen from the Earth. But first we will have to introduce some terminology. The limblimb of a object seen from a distance is the edge of the object. For example, the limb of a spherical object is a circle. The terminatorterminator of a non-luminous body is the line along its surface that separates day and night. For example, the terminator of a spherical object is a circle. The hornshorns (of crescent) of a crescentcrescent (phase) are the two points where the terminator crosses the limb of the body as seen by an observer. The horns are sharpest during the crescent phase, but continue to exist in every phase except full and new.
The following program keeps Venus’s horns
in a vertical line.
The vector
toSol
points from the Earth to the Sun,
and
toVenus
points from the Earth to Venus.
Their cross product
up
is perpendicular to both vectors.
It is parallel to the line segment connecting the horns as seen from Earth.
We will keep this vector vertical.
Two things can go wrong when we compute
up.
If Venus is directly in front of or behind the Sun,
toSol
and
toVenus
will be
colinearcolinear vectors
and their cross product will be the zero vector.
In this case,
we reuse the value of
up
from the previous iteration of the loop.
The other problem is that although
up
is vertical, it might be pointing up
(north towards
Draco)
or down (south towards
Dorado).
If
up
turns out to be more than
90°
away from Draco,
we negate it to keep it pointing north.
The time interval
dt
between frames,
about four Earth days,
keeps
Venus’s cloudsVenus, clouds of
in the same position in each snapshot.
See
solarDays
for its derivation.
--[[
Show the phases of Venus as seen from the Earth.
Make it look like the clouds are stationary.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "galaxies", "grid",
"markers")
celestia:hidelabel("constellations", "planets")
celestia:setambientCelestia:setambient(.05) --make night side of Venus barely visible
--telescopic view of Venus from Earth, 1.25 minutes of arc
observer:setfov(math.rad(1.25 / 60))
local sol = celestia:find("Sol")
local venus = celestia:find("Sol/Venus")
local earth = celestia:find("Sol/Earth")
celestia:select(venus)
--Make sure we can see the universe from the center of the Earth.
earth:setvisible(false)
--c is the number of Earth days it takes for the clouds to circle Venus
--with respect to the surface of Venus.
local speed = venus:getinfo().atmosphereCloudSpeed --in radians per day
assert (speed ~= 0, "can't divide by atmosphereCloudSpeed of 0")
local c = 2 * math.pi / speed
--dt is the number of Earth days it takes for the clouds to circle Venus
--with respect to the universal frame.
local r = venus:getinfo().rotationPeriod
local dt = r * c / (r + c)
celestia:settimescale(0) --Freeze the passage of time.
local lastUp = std.yaxis
while true do
celestia:settime(celestia:gettime() + dt) --Go dt days forward.
local earthPosition = earth:getposition()
local venusPosition = venus:getposition()
local toSol = sol:getposition() - earthPosition
local toVenus = venusPosition - earthPosition
local up = toSol ^ toVenus
if up:length() == 0 then
up = lastUp
elseif up:angle(std.yaxis) > math.rad(90) then
up = -- (vector unary minus operator)up --Point in the opposite direction.
end
observer:setposition(earthPosition)
observer:lookat(venusPosition, up)
lastUp = up
wait(1 / 4) --4 frames per second of real time
end
end
main()
We kept the horns in a vertical line,
at the price of rolling the planet around.
Now keep Venus’s north and south poles in a vertical line,
at the price of rolling the horns around.
Change the last argument of
Observer:lookatObserver:lookat
to
std.yaxis.
Display the phases of Earth as seen from Mars.
Since the Earth’s continents are more conspicuous than its clouds,
let
dt
be
earth:getinfo().rotationPeriod.
Better yet,
speed up the movie by letting
dt
be
8 * earth:getinfo().rotationPeriod.
See how the Celx standard library makes it possible to apply the
unary minus operator
to a vector object.
Read the
__unm__unm (in metatable)
method (two underscores)
in the
metatablemetatable (Lua)
for class
Vector
in
std.lua
(stdCelx).
Use the “lock frame” in
lockFrame
to keep the observer near the Earth,
looking at the Sun with the normal field of view.
Then call
Object:setradius
to make Venus big enough to see its phases from the Earth.
Any two vectors define a plane,
provided they are nonzero and non-colinear.
For example,
the following vectors
forward
and
up
lie in the YZ plane.
They are named after the most important application
of the maneuver we’re about to see.
Despite their names,
the two vectors are not perpendicular:
the angle between them is only
45°.
To rectify the situation
we will rotate
up
until it becomes perpendicular to
forward,
taking care to keep it in the YZ plane.
There are actually two vectors in the YZ plane that are perpendicular to
forward;
our new
up
will be the one that is less than
90°
from the original
up.
We first construct the vector
normal
perpendicular to the plane of
forward
and
up.
(Normalnormal (perpendicular) vectors
in this sense means “perpendicular”.)
We then construct the cross product
normal ^ forward,
which lies in the plane because it is perpendicular to
normal.
(As the proverb has it,
the enemy of my enemy is my friend.)
This cross product is also perpendicular to
forward.
We
normalize
it to simplify the output because we are interested only in its direction,
not its length.
(Normalnormalize a vector
in this sense means “of length 1”.)
Given any original values of
forward
and
up,
the angle between the original
up
and the new
up
will always less than
90°.
Changing
normal ^ forward
to
forward ^ normal
would make the angle greater than
90°.
In either case, the new
up
would still be perpendicular to
forward.
--[[
Given a pair of vectors, forward and up, keep up in the plane common to forward
and the original up, but make up perpendicular to forward. Rotate up by less
than 90 degrees.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local forward = celestia:newvector(0, 0, -1) --points away from us
local up = celestia:newvector(0, 1, -1) --up and away
local normal = forward ^ up
--Assert that forward and up are nonzero and non-colinear.
assert(normal:length() > 0, "forward and up do not define a plane")
up = (normal ^ forward):normalize() --up now perpendicular to forward.
local s = string.format("(%.15g, %.15g, %.15g)", up:getxyz())
celestia:print(s, 10)
wait()
end
main()
Fortunately, negative zero is equal to positive zero.
(-0, 1, 0)An easier way to do the same thing is is
local forward = celestia:newvector(0, 0, -1) --points away from us local up = celestia:newvector(0, 1, -1) --up and away up = forward:erectVector:erect(up) --up now perpendicular to forward, length = 1
See how
Vector:erect
has already been used to keep the observer on the Earth’s equator in
celestialSphere,
and to keep his forward vector from straying off the solstitial colure in
colures.
An observer’s orientationorientation gives the direction towards which he is looking and the direction towards his zenith. An orientation can therefore be represented by a forward vectorforward vector of orientation and an up vectorup vector of orientation. These vectors should ideally be perpendicular. If they are not, the forward vector takes precedence and the up vector is adjusted (“erected”) to accommodate it as we just saw in erect. For conversion between an orientation and the forward/up vectors that represent it, see forwardUp.
The observer’s
initial orientationorientation, default
is enshrined
in the standard library as
std.orientation0std.orientation0.
Its forward vector points along the negative Z axis of the universal frame,
towards the summer solstice
at RA 6h Dec
+23°
in
Taurus/GeminiTaurus/Gemini.
Its up vector points along the positive Y axis,
towards the north pole of the ecliptic
at RA 18h Dec
+67°
in
DracoDraco.
These two points lie along the
solstitial
coluresolstitial colure
in
colures.
Every orientation determines a pair of forward and up vectors. But not every pair of vectors represents an orientation. To represent an orientation, the forward and up vectors must be nonzero and non-colinearcolinear vectors, i.e., they must not lie in the same line. To test for these requirements, we can verify that the cross product of the two vectors is nonzero as we just did in erect.
Another way to represent an orientation is by the rotationrotation needed to get there from the initial orientation. And a rotation can be represented by a quaternionquaternion consisting of a real partreal part of quaternion and an imaginary partimaginary part of quaternion. The real part is a number giving the angle of the rotation, and the imaginary part is a vector giving the axis of the rotation. The value of the real part is the cosinecosine (trig function) of half of the angle of the rotation. This value ranges from 1 to –1 inclusive and represents a rotation of 0° to 360° inclusive. For example, a real value of 1/2 is the cosine of 45° and represents a rotation of 90°.
The length of the imaginary part is the sinesine (trig function) of half the angle of rotation. For example, the vector (1/2, 0, 0) has a length of 1/2, which is the sine of 45° and could represent a rotation of 90°. But we will never get the angle of rotation from the length of the imaginary part: that 1/2 is also the sine of 135°, and could represent a rotation of 270°. We will always get the angle from the real part.
The axis of the rotation always goes through the position of the observer. This means that the rotation can yaw, pitch, or roll him, but it cannot change his position. For example, our imaginary part of (1/2, 0, 0) does not represent a vector that starts at the Solar System Barycenter at (0, 0, 0) and goes to the point (1/2, 0, 0). It represents an axis that is parallel to this vector and that goes through his position.
Like a position and a vector,
a rotation object has numeric fields.
There are four of them,
hence the name
quaternion.
The real part is
w
and the imaginary part comprises
x,
y,
and
z.
The method
Rotation:realRotation:real
returns the number
w,
and
Rotation:imagRotation:imag
returns the vector
(x, y, z).
A rotation does not have the methods
getx,
gety,
getz,
and
getxyz.
A unit quaternionunit quaternion is one whose w2 + x2 + y2 + z2 = 1 It’s easy to prove that a quaternion representing a rotation is a unit quaternion. Give the angle of rotation θ, we have already said that w = cos θ 2 and x2 + y2 + z2 = ||v|| = sin θ 2 Therefore w2 + x2 + y2 + z2 = cos2 θ 2 + sin2 θ 2 = 1
Our description of a rotation must also include its direction. Let’s consider an observer rotating through an angle of 90° around the axis (1/2, 0, 0). To visualize the direction of the rotation, grasp the axis in your right hand with your thumb pointing away from the origin. (In this example, your thumb will be pointing to the right.) The direction in which the observer rotates will be the opposite of the direction in which your four non-thumb fingers point around the axis. In our case, the observer’s forward vector will pitch down. If we negate the angle to –90°, or negate the axis to (–1/2, 0, 0), the forward vector will pitch up.
The simplest orientation
is the observer’s initial orientation,
std.rotation0std.rotation0.
Its real part is 1,
which is the cosine of
0°
and represents a rotation of
0°.
Its imaginary part is the vector
(0, 0, 0),
whose length is the sine of
0°
and represents a rotation of
0°.
An object that represents the orientation of an observer will be called an
orientation
(getOrientation
and
setOrientation).
An object that represents a change in orientation,
instantaneous or animated,
will be called a
rotation
(rotateObserver).
And when we want to emphasize that an orientation or rotation contains
four numbers,
or when we multiply orientations or rotations together,
it will be called a
quaternion
(transformVector).
But all three of these data types are the
same classRotation (class)
of object in Celx,
and the
tostringtostring (Lua function)
function renders all three of them as
"[Rotation]".
For example,
The axis of a orientation or quaternion is always written with respect to the universal frame. The axis of a rotation is written in the frame of the object being rotated. For example, the rotation in randolph rotates a position written with respect to the Earth’s “ecliptic” frame of reference. The imaginary part of the rotation is therefore assumed to be a vector in that frame.
An orientation cannot be named
oror (Lua keyword),
which is a Lua
keywordkeyword (Lua).
The method
Observer:getorientationObserver:getorientation
returns the observer’s orientation
as a rotation whose imaginary part (the axis)
is always in universal coördinates.
We’ll display the angle of the rotation in degrees.
If the angle is
0°
or
360°,
the axis is of length zero and is irrelevant.
std.forwardstd.forward
and
std.upstd.up
are the forward and up vectors of the initial orientation
std.orientation0std.orientation0.
The tick handler
transformsRotation:transform
(transformVector)
them into
the forward and up vectors of the observer’s current orientation.
The function
vectorFormat
then converts the vector coördinates from the universal frame
(X axis pointing towards
Pisces,
Y towards
Draco)
toFrame:to
the
radecFrame
(X axis pointing towards
Pisces,
Y towards
Polaris).
A celestial
Object
has no
getorientation
method because we can get its orientation from the axes of its
“bodyfixed” frame
(bodyfixedFrame).
See also
Phase:getorientation.
--[[
Display the observer's orientation, initially std.orientation0.
To change his orientation, drag on the sky or press the arrow keys.
]]
require("std")
--variable used by tickHandler:
local observer = celestia:sane()
local radecFrame = celestia:newframe("universal", std.radecRotation)
local function vectorFormat(v)
assert(type(v) == "userdata" and tostring(v) == "[Vector]")
--Convert coordinates from universal frame to radecFrame.
--Then convert Cartesian coordinates to spherical.
local longlat = radecFrame:to(v):getlonglat()
--Break down radians into conventional units.
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
return string.format(
"(%g, %g, %g)\n"
.. "points towards RA %dh %dm %gs "
.. "Dec %s%d%s %d%s %g%s",
v:getx(), v:gety(), v:getz(),
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
end
local function tickHandler()
local orientation = observer:getorientation()
assert(type(orientation) == "userdata"
and tostring(orientation) == "[Rotation]")
local real = orientation:real()
assert(type(real) == "number")
local s = string.format("The angle of rotation is %g%s.\n\n",
math.deg(2 * math.acosmath.acos(real)), std.char.degree)
if math.absmath.abs(real) ~= 1 then --angle of rotation is not 0 or 360
local axis = orientation:imag()
assert(type(axis) == "userdata" and
tostring(axis) == "[Vector]")
s = s .. string.format("The axis of rotation %s.\n\n",
vectorFormat(axis))
end
s = s .. string.format(
"The forward vector %s.\n\n"
.. "The up vector %s.",
vectorFormat(orientation:transform(std.forward)),
vectorFormat(orientation:transform(std.up)))
--The observer's forward vector always points towards the center of the
--window. Mark the center with MM.
celestia:mmprint(s)
end
local function main()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
The first diagram and box of output show the initial orientation aimed at Taurus/GeminiTaurus/Gemini. The forward and up vectors point along the negative Z and positive Y axes respectively.
MM The angle of rotation is 0°. The forward vector (-0, -0, -1) points towards RA 6h 0m 0s Dec +23° 26′ 21.448″. The up vector (0, 1, 0) points towards RA 18h 0m 0s Dec +66° 33′ 38.552″.
The second diagram and output result from pitching the user
23°
down to Orion.
This angle is the tilt of the
Earth’s
axis with respect to the ecliptic,
known in radians as
std.tiltstd.tilt.
The
–0.397777
and
0.917482
are the sine and cosine of
–23°.
The
0.203123
is the sine of half of
23°.
An orientation is supposed to be a unit quaternion. How close is the following expression to 1?
orientation:real()^2 + orientation:imag():length()^2
Tired of gazing into the summer solstice in Taurus/GeminiTaurus/Gemini? Let’s pitch the observer’s direction of view down through an angle of 23° along the solstitial colure. We will leave him pointing at RA 6h Dec 0° on the celestial equator, directly below the solstice and to the left of Orion’s liver.
The method
Celestia:newrotationCelestia:newrotation
creates and returns a new orientation.
But the two arguments of
this method are very different from the return values we got from
Rotation:realRotation:real
and
Rotation:imagRotation:imag.
The first argument of
newrotation
is a unit vector in universal coördinates,
while the return value of
imag
was a unit vector times the sine of half the angle of rotation.
The second argument of
newrotation
is the angle of rotation in radians,
while the return value of
real
was the cosine of half the angle.
The following orientation
orion
differs from the initial orientation
by a
23°
rotation around the X axis,
pitching the observer’s direction of view down.
Equivalently,
we could say that the universe pitched upwards.
Had we sneaked a peek to our right,
away from the observer along the positive X axis,
we would have seen the universe turn clockwise.
--[[
Point the observer at Orion, with Polaris overhead. In other words,
point his forward vector at Orion, and his up vector at Polaris.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position) --Get away from the Sun's glare.
local axis = celestia:newvector(1, 0, 0) --axis of rotation
local theta = std.tilt --angle of rotation
--Think of orion as the orientation produced by the rotation.
local orion = celestia:newrotation(axis, theta)
assert(type(orion) == "userdata" and tostring(orion) == "[Rotation]")
observer:setorientationObserver:setorientation(orion)
celestia:mmprint("", 60)
wait()
end
main()
Create the same orientation by specifying its forwardforward vector of orientation and upup vector of orientation vectors. See forwardUp.
local toOrion = celestia:newvectorradec(math.rad(360 * 6 / 24), math.rad(0)) local toPolaris = celestia:newvectorradec(math.rad(0), math.rad(90)) local orion = celestia:newrotationforwardup(toOrion, toPolaris)
A
spherical linear interpolationspherical linear interpolation
(slerpslerp (spherical linear interpolation))
produces the average of two orientations.
Verify that the following call to
Rotation:slerpRotation:slerp
leaves us dangling to the upper left of Orion’s raised elbow.
Is
orion:slerp(taurusGemini, .5)
the same as
taurusGemini:slerp(orion, .5)?
Try values from 0 to 1 inclusive as the second argument of
slerp.
“Location, he used to say,” said the Navigator. “Universal location at every minute, every second. All you have to have is the key.”
“What key?” Cahill asked.
“A key like spherical trig, for one thing. If you can work it, and sight on some things up there in God’s heaven, the universe will tell you where you are, and will not fail to tell you. It can’t. It’s locked around your key. All you have to do is turn it. It’s complicated, but it works.… Mathematics, and especially astronomy, he called precision mysticism.
The method
Observer:setorientationObserver:setorientation
in
setOrientation
ignored and obliterated the observer’s existing orientation.
A more incremental approach would be to produce his new orientation
by applying a rotation to the existing one.
The following program does this,
leaving him in the same orientation as the previous program.
The name of the object has been changed from
orion
to
down
to
encourage us to think of it as a rotation downwards
rather than an orientation.
The punchline has been changed from
Observer:setorientation
to
Observer:rotateObserver:rotate.
The coördinates of the axis (imaginary part) of the orientation
passed to
Observer:setorientation
are measured with respect to the universal frame.
But the coördinates of the
axis of the rotation passed to
Observer:rotate
are measured with respect to the observer’s
personal frameobserver’s personal frame.
In this frame,
the origin is the observer’s current position.
The X axis points towards his current right,
the Y axis towards his current zenith,
and the Z axis towards his current rear.
In his initial orientation,
the axes of his personal frame are therefore parallel to those of the
universal frame,
and a
rotate
will have the same effect as a
setorientation
with the same argument.
But the observer’s personal frame changes with his orientation.
The next
rotate
will not have the same effect as a
setorientation.
Our rotation takes place instantly.
To animate it over time, see
animateRotation.
For future use,
we also show the
conjugate of a rotationconjugate of rotation.
Officially, the conjugate has the same angle (real part)
as the original rotation,
but its axis points in the opposite direction.
Unofficially,
the conjugate has the same axis as the original rotation,
but the opposite angle.
For example, the conjugate of
down
is
up.
The unofficial definition is simpler to visualize,
but the official definition keeps angle of rotation nonnegative.
--[[
Rotate the observer 23 degrees down from his previous orientation.
Leave him pointing towards Orion.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position) --Get away from the Sun's glare.
--Four rotations.
local down = celestia:newrotation(std.xaxis, std.tilt)
local right = celestia:newrotation(std.yaxis, math.rad(90))
local up = down:conjugateRotation:conjugate() --could also say local up = down ^^ (conjugate operator) -1
local left = right:conjugate()
assert(type(up) == "userdata" and tostring(up) == "[Rotation]")
observer:rotate(down) --instantaneous, not animated
celestia:mmprint("", 60)
wait()
end
main()
Pitch the observer a total of 46° down from the initial orientation. Leave him pointing below Orion’s feet, at his pet rabbit LepusLepus the Hare.
observer:rotate(down) observer:rotate(down) --cumulative effect --The observer is now aimed at Lepus the Hare. --Polaris is no longer overhead; it's now above and behind him.
Note that the following code will not take us down to Lepus.
The value
2 *
is not a
unit quaternion
at all
(orientation);
it is merely
* (scalar times quaternion operator)
downdown
with the
w,
x,
y,
z
coördinates doubled.
observer:rotate(2 * down)
The desired effect may be obtained by
the “quaternion multiplication”
in
quaternionMultiplication.
observer:rotate(down * down) --two applications of down
--The observer is now aimed at Lepus the Hare.
Change the rotation to the following.
observer:rotate(right)
This yaws the observer
90°
to the right.
It slides his target of view
(his forward vector)
along the red ecliptic to the vernal equinox in
Pisces.
He rotates around his Y axis,
which is currently the Y axis of the universal frame
and the axis of the ecliptic.
The ecliptic remains horizontal during the rotation,
proving that the north pole of the ecliptic in
Draco
remains directly overhead (at his up vector).
But check it anyway.
Turn on
Celestia:show("eclipticgrid")
and pan upwards with the down arrow.
You should find the crook of Draco at the observer’s zenith.
Change the rotation to the following. observer:rotate(down) observer:rotate(right) Observe that we end up with the same forward vector as in the previous exercise, pointing towards the vernal equinox in Pisces. But our up vector is different. This time it is the celestial equator that is horizontal, proving that Polaris is overhead.
The
down
rotation pitched the observer down,
rotating him around his X axis which points to his right.
His Y axis now points towards his new zenith,
at the north celestial pole near
Polaris.
Then the
right
rotation yawed him to the right around his Y axis,
sliding his point of view along the celestial equator from
Orion
to
Pisces.
His zenith remained at Polaris during the slide.
Change the rotation to the following.
observer:rotate(right)
observer:rotate(down)
We are now deposited at
CetusCetus
the Whale—uncharted
territory along the
equinoctial colure,
23°
below the vernal equinox in
Pisces.
The whale looks sort of like a big
Big DipperBig Dipper.
How did we get here?
First the
right
rotation yawed the observer’s point of view to
Pisces,
with
Draco
remaining overhead.
The observer’s X axis is now parallel to the universal Z axis.
It points towards
SagittariusSagittarius,
a constellation that is usually directly behind us.
Then the
down
rotation pitched him down around his X axis.
Draco
is no longer overhead;
it is now above and behind the observer’s zenith.
We can still get to
Draco
very easily from our new orientation.
Show the
"eclipticgrid"
and observe that the line of ecliptic longitude through the center of the
window is vertical.
Then press the down arrow key to pan upwards along this line
until we reach the crook of
Draco.
Since our starting point in
Cetus
is below the ecliptic,
we will have to pan up more than
90°.
We have just discovered that changing the order of the rotations can change the resulting orientation. Our mathematician friend would say that a series of rotations is not commutativecommutativity, rotation multiplication lacking in.
The
down
and
up
rotations in the following program
would pitch the observer
23°
down and
23°
up,
leaving his orientation unchanged.
With
quaternion multiplication
we can combine them into a single rotation with the same effect,
namely,
no effect at all.
--[[
Multiply a pair of quaternions.
The product leaves the observer in the initial orientation.
]]
require("std")
local function main()
local observer = celestia:sane()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
local down = celestia:newrotation(std.xaxis, std.tilt)
local up = down:conjugateRotation:conjugate()
local rotation = up ** (quaternion times quaternion operator) down --quaternion multiplication
assert(type(rotation) == "userdata" and
tostring(rotation) == "[Rotation]")
observer:rotate(rotation)
celestia:mmprint("", 60)
wait()
end
main()
The product
up * down
just happens to be equal to
down * up.
But we usually won’t be so lucky:
quaternion multiplication is not commutative.
This should come as no surprise,
because the series of
rotates
we just saw in
rotateObserver
was not commutative.
In fact,
the following program demonstrates
the non-commutativity of quaternion multiplication
with our old friends
down
and
right.
--[[
Multiply a pair of quaternions in one order.
You can edit the program and run it again to try them in the opposite order.
]]
require("std")
local function main()
local observer = celestia:sane()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
local down = celestia:newrotation(std.xaxis, std.tilt)
local right = celestia:newrotation(std.yaxis, math.rad(90))
observer:setorientation(right * down)
celestia:mmprint("", 60)
wait()
end
main()
The above
Observer:setorientation
has the same result as the following series.
observer:rotate(down)
observer:rotate(right)
It leaves us at the vernal equinox in
Pisces
with the
north
celestial polenorth celestial pole
overhead.
(Note that the celestial equator is horizontal.)
Incidentally,
we would have gotten the same result from the following,
since we are starting from the initial orientation.
We offer a pair of equivalent interpretations of the product
right * down.
They yield the identical result.
right * down
can be read from right to left,
taking the coördinates of the axis of each rotation
to be in the
observer’s personal frame.
First
down
pitches him
23°
down
around the X axis of the observer’s frame,
which is parallel at this time to the X axis of the universal frame.
This moves his target of view down the solstitial colure to
RA 0h Dec
0°,
and moves his zenith to
Polaris.
Then
right
yaws him
90°
to the right
around the Y axis of the observer’s frame,
which is parallel at this time to the Earth’s axis.
This moves his target of view to the right along the celestial equator
to the vernal equinox in
Pisces.
His zenith remains at
Polaris.
right * down
can be read from left to right,
taking the coördinates of the axis of each rotation
to be in the universal frame.
First
right
yaws him
90°
to the right
around the Y axis of the universal frame,
which is the axis of the ecliptic.
This moves his target of view
to the right along the ecliptic to the vernal equinox.
His zenith remains at
Draco.
Then
down
rolls him
23°
counterclockwise around the X axis of the universal frame.
But this does not move his target of view at all,
since he is already looking along the X axis.
It merely causes the picture he sees to roll
23°
clockwise.
The celestial equator becomes horizontal
and his zenith moves along the solstitial colure to
Polaris.
The two interpretations leave the user in the same orientation, with the same target of view and the same zenith. We will watch a movie of each interpretation in animateRotation.
Change the
Observer:setorientation
in the above program to
observer:setorientation(down * right)
and observe that it has the same effect as the following.
observer:rotate(right)
observer:rotate(down)
It leaves us down in
CetusCetus,
with
Draco
above and behind us.
Instead of an instantaneous rotation,
let’s make a movie of an observer
rotating to his new orientation over a period of several seconds.
The method we will use,
Observer:gotoObserver:goto,
can change his position as well as his orientation.
For now,
we will change only his orientation.
Observer:goto
receives a table of parameters,
some of whose field names have embedded uppercase letters.
The
duration
field is the number of real-time seconds it will take to get to the new
position;
the default value of 5 is in
std.durationstd.duration.
The
accelTime
is fraction of the first half of this duration
that will be spent in acceleration.
The same fraction of the second half will be spent in deceleration.
With our
accelTime
of .5,
we will accelerate for the first quarter of the duration (1.25 seconds),
move at a constant speed for the middle half (2.5 seconds),
and decelerate for the last quarter (1.25 seconds).
The
accelTime
is clamped to the range .1 to 1 inclusive;
the default is .5.
The
from
and
to
fields are the starting and ending positions,
defaulting to the observer’s current position.
The
initialOrientation
and
finalOrientation
fields are the starting and ending orientations,
defaulting to his current orientation.
The
startInterpolation
field is the fraction of the duration that should elapse
before the change of orientation begins.
The
endInterpolation
field is the fraction that should elapse
after the change of orientation has finished.
They default to .25 and .75,
which would confine the change of orientation
to the middle half of the duration of the
goto.
Our values of 0 and 1
ensure that the change of orientation
will occupy the entire five-second duration.
For the exact path through space and time
that the observer will follow during the
goto,
see
Exponential.
--[[
Animate a rotation: take 5 seconds to rotate 23 degrees from Taurus/Gemini
down to Orion.
]]
require("std")
local function main()
local observer = celestia:sane()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
wait(std.logo) --until "CELESTIA" logo disappears
celestia:mmprint("", 60) --mark the observer's direction of view
--A table of parameters for the goto. The duration, accelTime, from,
--to, and initialOrientation fields have their default values.
local parameters = {
duration = std.duration,
accelTime = .5, --accelerate for first quarter of duration
from = observer:getposition(),
to = observer:getposition(),
initialOrientation = observer:getorientation(),
finalOrientation = celestia:newrotation(std.xaxis, std.tilt),
startInterpolation = 0, --0 means start of the duration
endInterpolation = 1 --1 means end of the duration
}
observer:goto(parameters)
wait(parameters.duration) --until the goto is finished
end
main()
Now let’s dramatize the first interpretation of
right *quaternion multiplication down
that we saw in
quaternionMultiplication.
The following program decomposes it into two rotations,
with a
90°
change of direction between them,
and animates them separately.
We end up at the vernal equinox in
Pisces
with the
north
celestial polenorth celestial pole
overhead.
This program and the following exercise are the most important examples in the book.
--[[
Animate a series of rotations: first down, then right.
]]
require("std")
local function main()
local observer = celestia:sane()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
local down = celestia:newrotation(std.xaxis, std.tilt)
local right = celestia:newrotation(std.yaxis, math.rad(90))
wait(std.logo) --until "CELESTIA" logo disappears
celestia:mmprint("", 2 * std.duration + 3)
--Rotate around X axis of observer's frame,
--parallel to X axis of universal frame.
local parameters = {
finalOrientation = down, --First pitch down.
startInterpolation = 0,
endInterpolation = 1
}
observer:goto(parameters)
wait(std.duration) --Don't do the next goto until this one is finished.
--Rotate around Y axis of observer's frame,
--parallel to Earth's axis.
parameters.finalOrientation = right * down --Then yaw right.
observer:goto(parameters)
wait(std.duration)
end
main()
Decompose the second interpretation of
right * down
into two rotations and animate them separately.
In the above program,
change the
finalOrientation
of the first
goto
to
right.
Make no other change.
You should still end up at the vernal equinox in
Pisces
with the
north celestial pole
overhead.
Turn on the ecliptic grid and
animate the two interpretations of the product
down * right.
In both cases
you should end up in
CetusCetus
the Whale,
with the north pole of the ecliptic in
Draco
above and behind you.
Quaternion multiplication is
associativeassociativity of quaternion multiplication.
Animate an example using the following rotations.
local down = celestia:newrotation(std.xaxis, std.tilt)
local right = celestia:newrotation(std.yaxis, math.rad(90))
local clockwise = celestia:newrotation(std.zaxis, math.rad(90))
The two products
(clockwise * right) * down
should leave us in the same orientation.
Starting from the initial orientation
clockwise * (right * down)std.orientation0,
we will be left pointing at the vernal equinox in
Pisces
with the
north celestial pole
to our left.
We have two notations for taking the
conjugateconjugate of rotation
of a rotation
(rotateObserver).
local down = celestia:newrotation(std.xaxis, std.tilt)
local up = down:conjugateRotation:conjugate()
local up = down^^ (conjugate operator)-1 --exactly the same
We will use the second notation in a foray into the realm of
Abstract
AlgebraAbstract Algebra.
Call
setorientation(right * down)
to aim the observer at
Pisces,
with
Polaris
overhead.
Then demonstrate that we can get him back to the initial orientation
with either of the following.
Our mathematician friend would express this as follows. (r1r2)–1 = r2–1r1–1 He or she would say that it opens a vista of great formal beauty.
Congratulations—you have survived your first encounters with quaternion multiplication. Perhaps you have the makings of a planetarium operator.
Now that we have rotated the observer, let’s rotate a vector. We’ll take the vector pointing towards Taurus/Gemini and pitch it down through an angle of 23°, pointing it towards RA 6h Dec 0° on the celestial equator in Orion. We will then display the right ascension and declination of this point. For a more substantial example, see Quasar.
--[[
Transform (i.e., rotate) a vector and print the result.
]]
require("std")
--variable used by vectorFormat:
local radecFrame = celestia:newframe("universal", std.radecRotation)
local function vectorFormat(v)
assert(type(v) == "userdata" and tostring(v) == "[Vector]")
--Convert v's coordinates from universal frame to radecFrame.
v = radecFrame:to(v)
--Convert v's coordinates from Cartesian to spherical.
local longlat = v:getlonglat()
--Break down radians into conventional units.
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
return string.format(
"(%g, %g, %g)"
.. " points towards RA %dh %dm %gs "
.. "Dec %s%d%s %d%s %g%s",
v:getx(), v:gety(), v:getz(),
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
end
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
--vector in universal coordinates pointing towards Taurus/Gemini
local v = celestia:newvector(0, 0, -1)
local s = "v = " .. vectorFormat(v) .. "\n"
local down = celestia:newrotation(std.xaxis, std.tilt)
local right = celestia:newrotation(std.yaxis, math.rad(90))
--vector in universal coordinates pointing towards RA 6h Dec 0 degrees,
--to the left of Orion's liver.
local w = down:transformRotation:transform(v)
assert(type(w) == "userdata" and tostring(w) == "[Vector]")
--Look in the direction that w is pointing towards,
--with std.yaxis pointing up.
assert((w ^ std.yaxis):length() > 0)
observer:lookat(observer:getposition() + w, std.yaxis)
s = s .. "w = " .. vectorFormat(w)
celestia:mmprint(s, 60)
wait()
end
main()
The .397777 and .917482 are the sine and cosine of 23°.
MM v = (0, 0, -1) points towards RA 6h 0m 0s Dec +23° 26′ 21.448″ w = (-0, -0.397777, -0.917482) points towards RA 6h 0m 0s Dec 0° 0′ 0″
The following program makes the same call to
Rotation:transformRotation:transform
as the previous program.
It does the same arithmetic and prints the same
x,
y,
z
coördinates.
But it places exactly the opposite interpretation on the output.
This time the vector does not move at all, remaining pointing towards RA 0h Dec 0° on the celestial equator in Orion. We first print the coördinates of the vector with respect to the axes of the J2000 coördinate system in j2000Equatorial, whose XZ plane is the plane of the Earth’s equator. Then we print the coördinates of the vector with respect to the universal frame, whose XZ plane is the plane of the ecliptic.
The rotation
down
in the previous program has been renamed
j2000ToUniversal.
Instead of rotating the vector down from the ecliptic to the equator,
we can equivalently think of it as rotating the XZ plane up
from the equator to the ecliptic.
Our vector was on the original XZ plane,
and is now below the new XZ plane.
The opposite rotation,
universalToJ2000,
will rotate the plane back down.
--[[
Create the unit vector pointing towards Orion, writing its x, y, z coordinates
in the J2000 equatorial coordinate system: X axis points towards Pisces, Y axis
towards Polaris, Z axis towards Sagittarius (away from Orion). Keep the vector
pointing towards Orion, but change its x, y, z values from J2000 to universal
coordinates.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
--Vector in J2000 equatorial coordinates pointing towards Orion.
--The vector will always point towards the same point in Orion.
local v = celestia:newvector(0, 0, -1)
local s = string.format(
"J2000 equatorial coordinates of Orion: (%g, %g, %g)\n",
v:getxyz())
--a.k.a. down
local j2000ToUniversal = celestia:newrotation(std.xaxis, std.tilt)
--a.k.a. up
local universalToJ2000 = j2000ToUniversal:conjugateRotation:conjugate()
--Rewrite v in universal coordinates.
v = j2000ToUniversal:transform(v)
s = s .. string.format("universal coordinates of Orion: (%g, %g, %g)\n",
v:getxyz())
celestia:mmprint(s, 60)
observer:lookat(observer:getposition() + v, std.yaxis)
wait()
end
main()
MM
J2000 equatorial coordinates of Orion: (0, 0, -1)
universal coordinates of Orion: (-0, -0.397777, -0.917482)
Use the opposite quaternion,
universalToJ2000,
to change universal coördinates
back to J2000 equatorial coördinates.
Write
std.radecRotationstd.radecRotation
in place of
j2000ToUniversal.
It’s the same quaternion.
A vector and an observer respond differently when subjected to the same series of rotations. Let’s start with the vector. In the following example, all coördinates are in the universal frame.
local down = celestia:newrotation(std.xaxis, std.tilt) local right = celestia:newrotation(std.yaxis, math.rad(90)) --Point v towards Taurus/Gemini. local v = celestia:newvector(0, 0, -1) --Point v towards Orion. v = down:transform(v) --Point v towards Cetus. v = right:transform(v) --We could also do both of the above transformations in a single --statement. Note the order of the factors. --v = (down * right):transform(v)The vector ends up pointing to CetusCetus, 23° below the vernal equinox in Pisces. It got there by pitching down 23° around the universal X axis, and then yawing 90° to the right around the universal Y axis. A vector does not have its own set of axes or its own frame of reference. It always rotates around axes whose coördinates are in the universal frame.
Now let’s subject an observer to the same rotations,
down
and
right.
He ends up pointing at the vernal equinox in
Pisces,
with
Polaris
overhead.
He got there by pitching down
23°
around his X axis,
and then yawing
90°
to the right around his Y axis,
which is parallel at this time to the Earth’s Y axis.
An observer has a much richer inner life than a vector.
Why do both of the following transformations leave
v
pointing in the same direction, towards
Pisces?
What rotation would transform a vector pointing right into a vector pointing up? Obviously, the –90° rotation around the Z axis (0, 0, 1). But our rotations always have a nonegative angle, so we will write it as the 90° rotation around the negative Z axis (0, 0, –1). The 270° rotation around the Z axis would also do the trick, but it’s longer.
local right = std.xaxis --points to the right: (1, 0, 0) local rotation = celestia:newrotation(-std.zaxis, math.rad(90)) local up = rotation:transform(right) --points up: (0, 1, 0)
There’s an easy way to get the shortest rotation
that would transform a vector
v
into another vector
w,
at least if they are not colinear.
The axis of the rotation is supplied by the cross product of
v
and
w;
the angle is supplied by the dot product.
It’s almost as if the cross product
and dot product had been invented precisely for this purpose.
(Note that the following
Vector:angle
is implemented with a dot product).
local axis = w ^ v
assert(axis:length() > 0)
local rotation = celestia:newrotation(axis:normalize(), v:angle(w))
local t = rotation:transform(v)
--Within the limits of roundoff error, t == w.
assert(t:getx() == w:getx() and t:gety() == w:gety()
and t:getz() == w:getz())
See
Earthrise
for an example.
An orientation determines a forward vector and an up vector. Conversely, two nonzero, non-colinear vectors can be a forward and up vector determining an orientation.
The following code takes two vectors,
forward
and
up,
and creates the corresponding
orientation.
Ideally, the vectors are perpendicular.
If they are not,
the
forward
vector takes precedence
and the
up
vector is adjusted (erected) to accommodate it as in
erect.
As usual,
zero or
colinear vectors
would cause a
division by zero,
probably with spectacular results.
We will catch them with an
assert.
The orientation is created with
Position:orientationtoPosition:orientationto.
The position object to which this method belongs is called the
source position.
Our source position,
std.position0std.position0,
has the value
(0, 0, 0).
The arguments of
orientationto
are the same as the last two arguments of
Observer:lookatObserver:lookat.
The next-to-last argument is the
target position.
The vector from the source position to the target position
is the forward vector of the new orientation.
The last argument is the up vector of the new orientation,
erected if necessary.
Celestia:newrotationforwardup(forward, up)
To set the observer’s orientation
without creating a separate orientation object,
call
Observer:lookat.
The following code takes an
orientation
and creates the corresponding
forward
and
up
vectors.
The
std.forwardstd.forward
and
std.upstd.up
are the forward and up vectors of the initial orientation.
The
orientation
object is simply the rotation that would get us to the desired orientation
from the initial orientation.
Rotation:getforwardup()
A frame of reference serves two purposes in Celestia. First, the (x, y, z) coördinates of a position or vector are measured with respect to the X, Y, Z axes of a frame. Second, an observer can adhere to a frame, changing his position and orientation as the frame changes its position and orientation. By default, the frame to which the observer adheres is the universal frame in universalFrame, which is immobile. But there are many other frames.
Celestia offers six sets of frames,
identified by the case-sensitive strings passed to
Celestia:newframe
and returned from
Frame:getcoordinatesystem.
An alternative list of strings is used in a
cel:
URL.
Yet another list appears in the
lower right corner of the Celestia window,
which displays the frame to which the active observer has been
setframed.
See
Celestia:setoverlayelements.
argument of
Celestia:newframe
return value of Frame:getcoordinatesystem |
in argument of
Celestia:seturl
in return value of Celestia:geturl |
lower right corner
of Celestia window |
|---|---|---|
"universal" |
"Freeflight" |
"" |
"ecliptic" |
"Follow" |
"Follow" |
"equatorial" |
"Unknown" |
"" |
"bodyfixed" |
"SyncOrbit" |
"Sync Orbit" |
"chase" |
"Chase" |
"Chase" |
"lock" |
"PhaseLock" |
"Lock" |
There is only one universal frame for all of Celestia. See universalFrame.
There is one
ecliptic,
equatorial,
bodyfixed,
and
chase
frame for each celestial object.
The object is called the
reference objectreference object of frame
of the frame,
and may be a
planet, star, spacecraft,
a surface feature of a celestial object,
or even an abstraction such as the Solar System Barycenter.
In fact,
the reference object can be any object found with
Celestia:find.
There is one lock frame for each ordered pair of distinct celestial objects. They are called the reference object and the target objecttarget object of lock frame of the frame. The Earth and Mars have one lock frame, and Mars and the Earth have another. But the Earth and the Earth do not have a lock frame: it takes two to tango.
The
parentheses( ) (in pattern)
in the following
patternpattern (Lua)
delimit a
capturecapture (in pattern),
which is a substring to be returned by the
string.matchstring.find
method.
--[[
Print the name of the observer's current frame of reference.
]]
require("std")
local function main()
local observer = celestia:sane()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
local frameFrame (class) = observer:getframeObserver:getframe()
assert(type(frame) == "userdata" and tostring(frame) == "[Frame]")
local system = frame:getcoordinatesystemFrame:getcoordinatesystem()
assert(type(system) == "string")
local s = "The observer currently adheres to the " .. system .. " frame"
if system ~= "universal" then
local reference = frame:getrefobjectFrame:getrefobject()
assert(type(reference) == "userdata" and
tostring(reference) == "[Object]")
s = s .. "\nwhose reference object is " .. reference:name()
if system == "lock" then
local target = frame:gettargetobjectFrame:gettargetobject()
assert(type(target) == "userdata" and
tostring(target) == "[Object]")
s = s .. "\nand whose target object is "
.. target:name()
end
end
s = s .. ".\n"
local url = celestia:geturl()
local pattern = "^^ (anchor in pattern)cel://(.++ (in pattern))/" --the (.+) is a capture
local name = url:match(pattern)
s = s .. "The name of the frame in a URL is " .. name .. "."
celestia:print(s, std.duration)
end
main()
The observer currently adheres to the universal frame.
The name of the frame in a URL is Freeflight.
Each frame has an origin and three perpendicular axes named X, Y, Z. The Z axis for any frame is always determined by the X and Y axes using the right-hand ruleright-handed frame in framesOfReference. The following table groups the frames by their fundamental planefundamental plane (of frame) (framesOfReference).
The primaryprimary (of satellite) of a satellite is the object around which it revolves. For example, the primary of the Earth is the Sun.
| origin | fundamental plane | X axis | Y axis | Z axis | |
|---|---|---|---|---|---|
| universal
(universalFrame) |
Solar System Barycenter | XZ plane is
plane of ecliptic |
towards J2000 vernal equinox in Pisces |
towards
north pole of ecliptic in Draco |
towards J2000 winter solstice in Sagittarius |
| ecliptic
(eclipticFrame) |
center of
reference object |
XZ plane is plane of ecliptic |
towards J2000 vernal equinox in Pisces | towards north pole of ecliptic in Draco | towards J2000 winter solstice in Sagittarius |
| equatorial
(equatorialFrame) |
center of
reference object |
XZ plane is plane of reference object’s equator |
towards reference object’s current vernal equinox | towards north pole of reference object (south pole for Venus) | towards reference object’s current winter solstice (summer for Venus) |
| bodyfixed
(bodyfixedFrame) |
center of
reference object |
XZ plane is plane of reference object’s equator |
towards reference object’s 0° N 0° E | towards north pole of reference object (south pole for Venus) | towards reference object’s 0° N 90° W (90° E for Venus) |
| chase
(chaseFrame) |
center of
reference object |
XY plane is plane of reference object’s orbit around primary | away from direction of reference object’s motion w/r/t its primary | towards center of reference object’s primary (erected) | determined by X and Y axes |
| lock
(lockFrame) |
center of
reference object |
XY plane is plane of reference object’s motion w/r/t target object | towards center of target object | away from direction of reference object’s motion w/r/t target object (erected) | determined by X and Y axes |
The Y axis of the equatorial and bodyfixed frames points north
for most objects,
at least in the sense of pointing less than
90°
away
from the Y axis of the universal frame.
But an object with retrograde rotation has a Y axis that points south.
Examples include
VenusVenus, retrograde rotation of,
UranusUranus, retrograde rotation of
and its satellites,
PlutoPluto, retrograde rotation of
and its satellites,
and the asteroid
243 IdaIda (asteroid)
and its satellite
DactylDactyl (asteroid).
Thus a rotating object always spins counterclockwise
when viewed from a point on its positive Y axis.
An object with
no rotationrotation, lack of
has the Y axis of the universal frame.
Examples include
"Sol/Earth/Washington D.C.",
the
Solar System BarycenterSolar System barycenter, lack of rotation of,
and the
Milky WayMilky Way, lack of rotation of.
Stars other than the Sun also have the Y axis of the universal frame.
The X axis of the chase frame is defined in the above table. But the Y axis in the table is only an approximation to the real Y axis, which has to be exactly perpendicular to the X axis. The Y axis in the table is actually erected (adjusted, erect) to become perpendicular to the X axis. The real Y axis of the chase frame lies in the plane of the X and Y axes in the table, and is perpendicular to the X axis. The Y axis of the lock frame is handled similarly.
The Celx Standard Library lets us create a new frame of reference by rotating one of Celestia’s existing frames. For example, consider the set of axes in j2000Equatorial for the J2000 equatorial coördinates. Its origin is the Solar System Barycenter and its XZ plane is parallel to the plane of the Earth’s equator. The X axis points towards the vernal equinox in Pisces, and the Y axis towards the north celestial pole near Polaris. We can implement this frame as a 23° rotation of Celestia’s universal frame. We could also implement it as a 23° rotation of the Earth’s ecliptic frame; in this case the origin would be the center of the Earth. See rotatedRadec.
Other examples of “rotated” frames are the galactic and supergalactic coördinates (galacticCoordinates and supergalacticCoordinates), implemented as rotations of the universal or an ecliptic frame. And an altazimuth frame (celestialDome) for a point on the surface of a celestial object can be implemented as a rotation of the bodyfixed frame for that object. The angle and axis of the rotation depends on the latitude and longitude of the point.
Finally, each observer has his own
personal frameobserver’s personal frame,
a set of axes keyed to his current orientation.
This frame is used only by
Observer:rotateObserver:rotate
(rotateObserver)
and
Observer:orbitObserver:orbit
(orbitObserver).
For example,
the following code
rotates the observer around an axis that extends to his current right.
This axis is not necessarily parallel to the X axis of the universal frame.
Each celestial object has its own ecliptic frame of reference. The object is called the reference object of the frame. The ecliptic frame identical to the universal frame except that its origin is at the center of the reference object. If the reference object moves, the ecliptic frame moves with it.
The axes of an ecliptic frame remain parallel to those of the universal frame. The XZ plane is therefore parallel the plane of the ecliptic. The X axis points towards the vernal equinox at RA 0h in Pisces. The Z axis points towards the winter solstice at RA 18h in Sagittarius. The Y axis points towards the north pole of the ecliptic in Draco.
Let’s verify that the X axis of the Earth’s ecliptic frame points from the center of the planet towards Pisces, and the Y axis towards Draco. We will position the observer on the negative X axis. Looking towards the origin with the Y axis pointing up, the Earth should appear directly in front of us with Pisces behind it. Draco should be overhead because the red line of the ecliptic is horizontal.
The
position
object initially has its coördinates measured with respect to the
Earth’s ecliptic frame.
But a position or vector passed to
Observer:setposition
or
Observer:lookat
must always be in the coördinates of the universal frame.
(This is true even if the observer has been
setframeObserver:setframed
to another frame.)
The position must therefore be converted
from
the Earth’s ecliptic frame to the universal frame by the method
Frame:fromFrame:from.
The resulting object still represents the same position in space,
but the values of its
(x, y, z)
coördinates have been changed.
The conversion must be performed with
Frame:from
rather than
Rotation:transformRotation:trasnform
because the universal and ecliptic frames have different origins.
The Earth’s ecliptic frame is in constant motion
as the Earth revolves around the Sun.
By default,
Frame:from
translates a position from the ecliptic frame of the current time
to the universal frame.
An optional second argument of
Frame:from
lets us specify a different time.
The native Celx
Frame:from
accepts a position or an orientation as its argument.
The standard library lets this method accept a vector as well,
permitting us to create the
up
vector passed to
Observer:lookat.
(In this example we could change the last argument of
lookat
to plain old
std.yaxis,
because the axes of an ecliptic frame are parallel to those of the
universal frame.
But for most other frames, this would not be true.)
The opposite of
Frame:from
is
Frame:toFrame:to.
It converts a position, orientation, or vector from some other frame
to
the universal frame.
When we convert the position of the Earth from the universal frame to
the Earth’s ecliptic frame,
we always get
(0, 0, 0).
The center of the Earth is always at
the origin of the Earth’s ecliptic frame.
--[[
Demonstrate that the X axis of the Earth's ecliptic frame points towards Pisces,
and the Y axis towards Draco. Position the observer on the negative X axis and
look towards the origin, with the Y axis pointing up.
]]
require("std")
local function main()
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
local eclipticFrame = celestia:newframe("ecliptic", earth)
--Adhere the user to the eclipticFrame so he moves along with it.
--The setframe must come *before* the setposition.
observer:setframe(eclipticFrame)
--A position on the negative X axis of Earth's ecliptic frame.
--The coordinates of the position are in Earth's ecliptic frame.
local microlightyears = 12 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
local s = string.format(
"Observer in Earth's ecliptic frame: (%g, %g, %g)\n",
position:getxyz())
--The same position, but convert the coordinates
--from Earth's ecliptic frame to the universal frame.
position = eclipticFrame:from(position)
observer:setposition(position)
s = s .. string.format(
"Observer in universal frame: (%g, %g, %g)\n",
position:getxyz())
--The position of the Earth in the coordinates of the universal frame.
local universalPosition = earth:getposition()
s = s .. string.format(
"Center of Earth in universal frame: (%g, %g, %g)\n",
universalPosition:getxyz())
--The position of the Earth in the coordinates of the Earth's ecliptic
--frame. It will be (0, 0, 0) by definition.
local eclipticPosition = eclipticFrame:to(earth:getposition())
s = s .. string.format(
"Center of Earth in Earth's ecliptic frame: (%g, %g, %g)\n",
eclipticPosition:getxyz())
--A vector pointing along the Y axis of Earth's ecliptic frame.
--The coordinates are in Earth's ecliptic frame.
local up = celestia:newvector(0, 1, 0) --or std.yaxis
--The same vector, but convert the coordinates from Earth's ecliptic
--frame to the universal frame. (This conversion happens to leave the
--coordinates unchanged, but will be necessary for other frames.)
up = eclipticFrame:from(up)
observer:lookat(universalPosition, up)
celestia:print(s, 60)
wait()
end
main()
Observer in Earth's ecliptic frame: (-0.00809004, 0, 0)
Observer in universal frame: (1.67688, 0.00018605, 16.014)
Center of Earth in universal frame: (1.68497, 0.00018605, 16.014)
Center of Earth in Earth's ecliptic frame: (0, 0, 0)
Verify that the Z axis of the Earth’s ecliptic frame points towards the winter solstice in Sagittarius. Let the observer’s position be
--coordinates in the Earth's ecliptic frame local position = celestia:newposition(0, 0, -microlightyears)Then verify that the Y axis points towards the north pole of the ecliptic in Draco. The observer’s forward and up vectors cannot be colinear, so we will have to choose a different up vector.
--Coordinates in the Earth's ecliptic frame. local position = celestia:newposition(0, -microlightyears, 0) --Coordinates in the Earth's ecliptic frame. --Make solstitial colure vertical, with Polaris towards top of window. local up = celestia:newposition(0, 0, -1)Position the observer on the negative X axis of the Earth’s ecliptic frame, looking at hte Earth with the Y axis pointing up. Verify that he remains there even if we speed up the time.
--one minute of simulation time per second of real time celestia:settimescale(60)
Then comment out the call to
Observer:setframe,
run the program again,
and watch the Earth sail out of the window.
The moral is that the observer’s frame should be set
before
his position and orientation.
Display colored arrows along the axes of the Earth’s ecliptic frame.
local mark = {type = "frame axesframe axes"} --a table with one field
earth:addreferencemark(mark)
The table can be an anonymous object.
earth:addreferencemark({type = "frame axes"})
Since the only argument of the method is a table with curly braces,
the
parentheses( ) (omitted for table argument)
can be omitted.
earth:addreferencemark {type = "frame axes"}
To see all three arrows,
toggle the OpenGL wireframe mode with
control-w.
The arrows are labeled with unexpected names.
The red “X” arrow does indeed point along the positive X axis of the
Earth’s ecliptic frame.
But the blue “Z” arrow points along the positive Y axis,
and the green “Y” arrow points along the
negative
Z axis.
Verify that the axes of an ecliptic frame remain parallel to those of the
universal frame
even if the reference object belongs to a different solar system.
Try the
extrasolar planet
"Pollux/b"Pollux/b (extrasolar planet).
Read the
from
and
to
methods in the metatable for class
Frame
in the standard library file
std.lua
in
stdCelx.
The following program should position the observer at the center of the Earth. On Macintosh, it works correctly. But on Microsoft Windows, it places him at an unpredictable location, often lightyears—or megaparsecs—from the Earth. The same unpredictable behavior happens when Celestia is compiled from the source code on Macintosh, Microsoft Windows, or Linux.
--[[
Position the Observer at the center of the Earth,
i.e., at the origin of Earth's ecliptic frame.
]]
require("std")
local function main()
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
celestia:select(earth) --to display the observer's distance from Earth
earth:setvisible(false) --so the observer can see out of the Earth
local eclipticFrame = celestia:newframe("ecliptic", earth)
observer:setframe(eclipticFrame)
observer:setposition(earth:getposition())
wait()
end
main()
The
bugbug in Celestia
is in the C++ member function
Observer::orbit
in the file
version/src/celengine/observer.cpp.
It creates a vector
v
pointing from the origin of the observer’s frame to his position.
In this example,
the origin and the position are the same point,
so
v
is of length
zerodivision by zero
and is impossible to normalize.
The solution is to change the following code in
Observer::orbit
to
if (distance > 0) { //distance is the length of v v.normalize(); v *= distance; }Before you run the Celx program, can you predictnan (not a number) the Earth’s phase angle for an observer at the centernot a number (nan) of the Earth?
Let’s peek over the Earth’s shoulder at the retrograde motionapparent retrograde motion of MarsMars, retrograde motion of. We’ll pick the oppositionopposition of December 24, 2007 because Mars was then in Taurus/Gemini, the target of the observer’s initial orientation.
--[[
Show the apparent retrograde motion of Mars as seen from Earth
during the opposition of December 2007.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("grid", "orbits")
celestia:show("eclipticgrid")
celestia:hidelabel("moons", "planets", "spacecraft")
local earth = celestia:find("Sol/Earth")
local mars = celestia:find("Sol/Mars")
celestia:select(mars)
local eclipticFrame = celestia:newframe("ecliptic", earth)
--The observer will move with the Earth,
--but will keep the same orientation.
observer:setframe(eclipticFrame)
local microlightyears = 25 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(0, 0, microlightyears)
observer:setposition(eclipticFrame:from(position))
celestia:settime(celestia:utctotdb(2007, 10, 15))
--4 days of simulation time per second of real time.
celestia:settimescale(60 * 60 * 24 * 4)
wait()
end
main()
In traceRetrograde we will use OpenGL to draw the loop that Mars makes on the surface of the celestial sphere.
After setting the observer’s frame, you can set his orientation to whatever you want. The most bland example would be the orientation we already have.
--The initial orientation points towards Taurus/Gemini, with Draco up. local forward = celestia:newvectorradec(math.rad(360 * 6 / 24), std.tilt) local up = celestia:newvectorradec(math.rad(360 * 18 / 24), math.rad(90) - std.tilt) local orientation = celestia:newrotationforwardup(forward, up) observer:setorientation(orientation) --Simpler ways to create the same orientation: --local orientation = celestia:newrotationforwardup(std.forward, std.up) --local orientation = std.orientation0Display a caption as Mars’s direction of apparent motion changes: direct, retrograde, and direct again.
--variables used by tickHandler: local earth = celestia:find("Sol/Earth") local mars = celestia:find("Sol/Mars") local eclipticFrame = celestia:newframe("ecliptic", earth) local oldLongitude = nil --Mars's ecliptic longitude at previous tick local function tickHandler() --coordinates in universal frame local marsPosition = mars:getposition() --coordinates converted to Earth's ecliptic frame marsPosition = eclipticFrame:to(marsPosition) local longitude = marsPosition:getlonglat().longitude if oldLongitude ~= nil then --there was a previous call to tickHandler local s = nil if longitude > oldLongitude then --Mars is moving right to left s = std.char.larr .. " direct" --left arrow elseif longitude < oldLongitude then --moving left to right s = "retrograde " .. std.char.rarr else s = "stationary" end celestia:print(s, 1, 0, 0, -3, -5) end oldLongitude = longitude end --in the main function celestia:registereventhandler("tick", tickHandler) ← direct retrograde → ← direct
The above
tickHandler
has two bugs.
If Mars’s longitude is
359°
at one tick and
1°
at the next,
its motion is direct but the
tickHandler
prints
"retrograde".
Conversely, if the longitude is
1°
at one tick and
then
359°
at the next,
the motion is retrograde but the
tickHandler
prints
"direct".
Fix the bugs in the simplest way.
Did the furiously rotating Earth distract you?
If so,
keep the Earth out of the picture
by watching the retrograde motion from the side of the Earth facing Mars.
Position the observer along the
negative
Z axis of the Earth’s ecliptic frame,
at the top of the Earth’s atmosphere above the sub-summer-solstice point.
Change the above call to
Observer:setposition
to the following.
Don’t forget the uppercase H in
atmosphereHeight.
To verify that the Earth remains right behind us, too close to focus on, press ** (rear-view mirror command) (asterisk, the rear-view mirror command) while the program is running. Then press asterisk again to restore the view forward.
A simpler way to keep the Earth out of the picture is to make it invisible. This will let us position the observer at the center of the Earth.
earth:setvisible(false) local position = celestia:newposition(0, 0, 0) --or std.position0 observer:setposition(eclipticFrame:from(position)) --or simply --observer:setposition(earth:getposition())Tycho Brahe’s solar system was a compromise. His Sun revolved around a fixed Earth, and the other planets revolved around the Sun. Let’s simulate this.
--[[
View the Tychonic solar system from above the Earth, looking down.
Keep the Earth motionless in the center of the window,
in front of the south pole of the Ecliptic in Dorado.
The summer solstice in Taurus/Gemini is towards the top of the window.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "grid") --distracting
celestia:hidelabel("constellations")
celestia:show("orbits")
local earth = celestia:find("Sol/Earth")
local eclipticFrame = celestia:newframe("ecliptic", earth)
observer:setframe(eclipticFrame)
local position = celestia:newposition(0, 128, 0)
observer:setposition(eclipticFrame:from(position))
observer:lookat(eclipticFrame:from(std.position0), std.forward)
--2 days of simulation time per second of real time
celestia:settimescale(60 * 60 * 24 * 2)
wait()
end
main()
In traceRetrograde we will use OpenGL to draw the loops that Mars makes relative to the stationary Earth. These are the loops generated by the deferents and epicycles of the Ptolemaic solar systemPtolemaic solar system.
In the Copernican Solar SystemCopernican Solar System, the planets go around the Sun. Simulate this solar system with an ecliptic frame whose reference object is the Sun. In the Newtonian Solar System, the Sun and planets go around the Solar System Barycenter. Simulate this solar system with the universal frame.
In the Newtonian Solar System, make the planets big enough to see. For example,
local earth = celestia:find("Sol/Earth") local kilometers = earth:radius() earth:setradius(2400 * kilometers)Let’s display the right ascension and declination of BetelgeuseBetelgeuse (star) in OrionOrion as seen from the center of the Earth. The ideal frame of reference for this purpose would have its origin at the center of the Earth, with its XZ plane in the plane of the Earth’s J2000 equator. The X axis would point towards the vernal equinox in Pisces, and the Y axis towards the north celestial polenorth celestial pole near Polaris. This frame would be identical to the Earth’s ecliptic frame, except that it would be tilted therefrom by a rotation of 23° around the X axis of the ecliptic frame.
The Celx Standard Library lets us create the ideal frame very easily:
the following
radecRotation
is the rotation,
and the
radecFrame
is the frame.
The method
Frame:to
converts the coördinates of the position from the universal frame
(Y axis pointing towards
Draco)
to the
radecFrame
(Y axis pointing towards
Polaris).
Then
Position:getlonglat
converts the position’s Cartesian coördinates
into spherical coördinates,
including a radial coördinate giving the position’s distance
in microlightyears from the origin.
The function
std.torastd.tora
breaks down the radians of longitude into hours, minutes, and seconds
of right ascension,
and
std.todecstd.todec
breaks down the radians of latitude into degrees, minutes, and seconds
of declination.
std.todec
also provides the numeric field
signumsignum (of declination),
which is 1 for north,
–1
for south,
or 0 for the equator.
The function
std.signstd.sign
converts these numbers into the strings
"+",
"-",
or
"".
--[[
Print the right ascension and declination of Betelgeuse
as seen from the center of the Earth.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
local earth = celestia:find("Sol/Earth")
local betelgeuse = celestia:find("Betelgeuse")
celestia:select(betelgeuse)
local radecRotation = celestia:newrotation(std.xaxis, std.tilt)
local radecFrame = celestia:newframeCelestia:newframe("ecliptic", earth, radecRotation)
--[[
In the universal frame, std.yaxis points towards Draco.
In the radecFrame, std.yaxis points towards Polaris.
In the universal frame, up points towards Polaris.
]]
local position = betelgeuse:getposition()
local up = radecFrame:from(std.yaxis)
observer:lookat(position, up)
local s = string.format("Betelgeuse:\n"
.. "Position in universal frame: (%.15g, %.15g, %.15g)\n",
position:getxyz())
--Convert the coordinates of the position from the universal frame
--to the radecFrame.
position = radecFrame:to(position)
s = s .. string.format(
"Position in radecFrame: (%.15g, %.15g, %.15g)\n",
position:getxyz())
--Convert to polar coordinates.
local longlat = position:getlonglat()
assert(type(longlat) == "table")
--Convert radians to hours, minutes, seconds of right ascension.
local ra = std.tora(longlat.longitude)
assert(type(ra) == "table")
--Convert radians to degrees, minutes, seconds of declination.
local dec = std.todec(longlat.latitude)
assert(type(dec) == "table")
s = s .. string.format(
"RA %dh %dm %gs\n"
.. "Dec %s%d%s %d%s %g%s",
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
celestia:print(s, 60, -1, -1, 1, 6) --5 lines of text
wait()
end
main()
Betelgeuse:
Position in universal frame: (10402991.2948608, -137483581.542969, -478496673.583984)
Position in radecFrame: (10402989.5836485, 64196332.3193992, -493699957.529088)
RA 5h 55m 10.2892s
Dec +7° 24′ 25.3318″
Use the existing
std.radecRotationstd.radecRotation
instead of creating your own
radecRotation.
It’s the same rotation.
How much of a difference would it make
if we measured the right ascension and declination of Betelgeuse
as seen from the Solar System Barycenter?
Create a
radecFrame
whose origin is the barycenter.
It will be identical to the universal frame,
but tilted 23° therefrom.
Find the right ascension and declination of the Moon
as seen from
"Sol/Earth/Washington D.C."
at 12:00 UTC on January 1, 2014.
For now, just print the numbers.
We will position the observer and draw the picture
when we have the bodyfixed frame in
bodyfixedFrame.
Read the program in j2000Equatorial that displays the current right ascension and declination of the observer’s direction of view.
To create a rotated frame from an existing frame, we have supplied the axis and angle of the rotation. To create a rotated frame from an existing frame by supplying the X, Y, and Z axes of the rotated frame, see johnGlenn and Analemma.
The following
galacticFrame
is the same as the universal frame,
but is tilted therefrom by the
std.galacticRotationstd.galacticRotation.
For those who are interested,
the angle of the
std.galacticRotation
is approximately
174°
and the axis of rotation points towards the lower reaches of
EridanusEridanus.
But it is much more important to know where the axes of the
galacticFrame
are pointing.
The
galacticFrame
has the origin as the universal frame,
the Solar System Barycenter.
The XZ plane of the
galacticFrame
is the plane of the Milky Way galaxy.
The X axis points towards the
galactic
centergalactic center
in
SagittariusSagittarius;
the Z axis towards
VelaVela
the Sail.
The Y axis points towards the
north galactic polenorth galactic pole (NGP)
(NGPNGP (north galactic pole))
in
Coma
BerenicesComa Berenices,
and away from the
south galactic polesouth galactic pole (SGP)
(SGPSGP (south galactic pole))
in
SculptorScultor.
Galactic longitudegalactic longitude (ℓ)
is denoted by
ℓℓ (galactic longitude).
This character
(a script lowercase L)
is in the standard library as
std.char.lstd.char.l (galactic longitude).
Galactic latitudegalactic latitude (b)
is denoted by an italic
bb (galactic latitude).
Looking down at the XZ plane from
Coma Berenices,
the positive Y axis points straight towards us and is invisible:
For a totally different system of coördinates whose origin is at the center of the galaxy, see the bodyfixed frame in alternativeBodyfixed.
The vector
forward
in the following
main
function is
(1, 0, 0).
Interpreted in universal coördinates,
it would therefore point towards RA 0h
Dec 0°
in
Pisces.
But we will interpret it as a vector in galactic coördinates,
pointing towards the galactic center at
ℓ = 0°
b = 0°
in
Sagittarius.
Before we use it to build an orientation,
we must convert its coördinates
from
the
galacticFrame
to the universal frame.
--[[
Display the galactic coordinates of the direction in which the observer is
facing. He is initially facing the galactic center in Sagittarius, with the
north galactic pole in Coma Berenices overhead.
To change his orientation, press the arrow keys or drag on the sky.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local galacticFrame = celestia:newframe("universal", std.galacticRotation)
local function tickHandler()
--Get the observer's forward vector in universal frame coordinates.
local forward = observer:getorientation():transform(std.forward)
--Rewrite the observer's forward vector in galacticFrame coordinates.
forward = galacticFrame:to(forward)
--Convert cartesian coordinates to spherical.
local longlat = forward:getlonglat()
local s = string.format(
"%s = %.2f%s\n"
.. "b = %.2f%s",
std.char.l, math.deg(longlat.longitude), std.char.degree,
math.deg(longlat.latitude), std.char.degree)
celestia:mmprint(s, 1)
end
local function main()
observer:setposition(std.position) --Get away from Sun's glare.
celestia:hide("grid", "ecliptic")
celestia:show("galacticgridgalacticgrid (renderflag) ")
--celestia:setgalaxylightgainCelestia:setgalaxylightgain(.75) --minimum 0, maximum 1, default .5
--Point the observer at the center of galaxy,
--with north galactic pole overhead.
local forward = celestia:newvectorlonglat(math.rad( 0), math.rad( 0))
local up = celestia:newvectorlonglat(math.rad( 0), math.rad(90))
local orientation = celestia:newrotationforwardup(
galacticFrame:from(forward),
galacticFrame:from(up))
observer:setorientation(orientation)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
MM
ℓ = 360.00°
b = -0.00°
To remove any jitterjitter (of numeric value) in the values of ℓ and b, see celestialDome. To display 360° as 0°, see j2000Equatorial.
The argument of
Frame:fromFrame:from
can be a
Rotation
instead of a
Vector.
In the above
main
function,
we can therefore change
local orientation = celestia:newrotationforwardup(
galacticFrame:from(forward),
galacticFrame:from(up))
observer:setorientation(orientation)
to
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(galacticFrame:from(orientation))
The radio source Sagittarius A*Sagittarius A* (radio source) is a supermassive black holeblack hole at RA 17h 45m 40.0409s Dec –29° 0′ 28.118″. Since it’s at the center of the Milky Way, its galactic coördinates should be close to ℓ = 0°, b = 0°. Are they?
--RA and Dec of Sagittarius A* in radians local ra = math.rad(( 17 + (45 + 40.0409 / 60) / 60) * 360 / 24) local dec = math.rad( -29 - ( 0 + 28.118 / 60) / 60) local toSagittariusA = celestia:newvectorradec(ra, dec) --Convert vector from universal frame to galacticFrame. toSagittariusA = galacticFrame:to(toSagittariusA) --Convert cartesian coordinates to spherical. local longlat = toSagittariusA:getlonglat() local s = string.format( "%s = %.15g%s\n" .. "b = %.15g%s", std.char.l, math.deg(longlat.longitude), std.char.degree, math.deg(longlat.latitude), std.char.degree) ℓ = 359.944285593245° b = -0.0461371244601728°The Hubble Deep FieldHubble Deep Field is a small area of the sky at RA 12h 36m 49.4s Dec 62° 12′ 58″ in Ursa MajorUrsa Major. It was chosen to be well away from the plane of the galaxy, which is filled with gas and dust. What is the field’s galactic latitude (b)?
In the real universe,
the
Milky Way
and the
Andromeda Galaxy
("M 31"M31 (Andromeda Galaxy))
spin in opposite directions.
Demonstrate that in the Celestia universe,
they spin in the same direction.
The following program displays the Milky Way centered in the window. The observer is above the north pole of the galaxy; the galactic grid confirms that he is looking down, towards the south galactic pole. The trailing arms show that the galaxy spins clockwise, as in the real universe.
--[[
Position the observer above the north pole of the Milky Way
and look down at the galaxy.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("ecliptic", "grid")
celestia:show("galacticgrid") --Look towards south galactic pole.
local galacticFrame =
celestia:newframe("universal", std.galacticRotation)
observer:setframe(galacticFrame)
local galaxy = celestia:find(
"Milky Way"
--"M 31"
)
local microlightyears = 5 * galaxy:getinfo().radius * 1000000
local vector = celestia:newvector(0, microlightyears, 0)
local position = galaxy:getposition() + galacticFrame:from(vector)
observer:setposition(position)
observer:lookat(galaxy:getposition(), galacticFrame:from(std.xaxis))
wait()
end
main()
Now change the galaxy to
"M 31"
(with one space).
Note that the observer remains in the same orientation,
pointing towards the south pole of the galactic grid.
(The galactic grid is still the grid of the Milky Way.)
The Andromeda Galaxy is centered in front of him,
although it does not lie perfectly flat in the plane of the window.
Its trailing arms show that it spins clockwise.
The supergalactic planesupergalactic plane is the plane of the nearest superclusterssupercluster of galaxies, including the Hydra-Centaurus SuperclusterHydra-Centaurus Supercluster the Perseus-Pisces SuperclusterPerseus-Pisces Supercluster, the Pavo-Indus SuperclusterPavo-Indus Supercluster, and our own Virgo SuperclusterVirgo Supercluster. Above and below the plane lie the NorthernNorthern Local Supervoid and SouthernSouthern Local Supervoid Local Supervoidsvoid (intergalactic).
The following
supergalacticFrame
is the same as the universal frame,
but is tilted therefrom by the
std.supergalacticRotationstd.supergalacticRotation.
The XZ plane of the
supergalacticFrame
is the supergalactic plane.
The X axis points towards
CassiopeiaCassiopeia,
where the galactic and supergalactic planes cross each other.
The Y axis points towards the
north supergalactic poleat
galactic coördinates
ℓ = 47.37°,
b = +6.32°
in
HerculesHercules;
the
south polesouth supergalactic pole
is in
Canis MajorCanis Major.
Supergalactic longitudesupergalactic longitude (SGL) and latitudesupergalactic latitude (SGB) are denoted by uppercase SGLSGL (supergalactic longitude) and SGBSGB (supergalactic latitude) respectively. Looking down at the XZ plane from Hercules, the positive Y axis points straight towards us and is invisible:
It is to be hoped that a future version of Celestia will display a supergalactic grid. For the time being, the following program draws the supergalactic plane.
--[[
Display the supergalactic coordinates of the direction in which the observer is
facing. He is initially facing the Virgo Cluster (the center of the Virgo
Supercluster), with the north supergalactic pole in Hercules overhead. To
change his orientation, press the arrow keys or drag on the sky.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local supergalacticFrame =
celestia:newframe("universal", std.supergalacticRotation)
local function tickHandler()
--Get the observer's forward vector in universal frame coordinates.
local forward = observer:getorientation():transform(std.forward)
--Rewrite observer's forward vector in supergalacticFrame coordinates.
forward = supergalacticFrame:to(forward)
--Convert cartesian coordinates to spherical.
local longlat = forward:getlonglat()
local s = string.format(
"SGL = %.2f%s\n"
.. "SGB = %.2f%s",
math.deg(longlat.longitude), std.char.degree,
math.deg(longlat.latitude), std.char.degree)
celestia:mmprint(s, 1)
end
local function main()
observer:setposition(std.position) --Get away from Sun's glare.
celestia:hide("grid", "ecliptic")
celestia:show("galacticgrid")
--Draw the line of the supergalactic plane
--by marking the galaxies within 1.5 degrees of it.
for dso in celestia:dsos() do
if dso:getinfo().type == "galaxy"
and dso:name() ~= "Milky Way" then
local galaxyPosition = dso:getposition()
galaxyPosition = supergalacticFrame:to(galaxyPosition)
local longlat = galaxyPosition:getlonglat()
if math.degmath.deg(math.absmath.abs(longlat.latitude)) < 1.5 then
dso:markObject:mark("white", "plus", 10)
end
end
end
--Point the observer at the Virgo Cluster,
--with north supergalactic pole overhead.
local forward = celestia:newvectorlonglat(math.rad(104), math.rad(-2))
local up = celestia:newvectorlonglat(math.rad( 0), math.rad(90))
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(supergalacticFrame:from(orientation))
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
MM
SGL = 104.00°
SGB = -2.00°
Press
.
(period) to widen the field of view,
and control-b to display the constellation boundaries.
Starting at
VirgoVirgo
and moving left, towards higher supergalactic longitudes,
verify that the supergalactic plane goes through the constellation pairs
HydraHydra
and
CentaurusCentaurus,
PavoPavo
and
IndusIndus,
and
PiscesPisces
and
PerseusPerseus.
We’ll have a better way to draw the supergalactic equator in
traceRetrograde.
The Virgo ClusterVirgo Cluster (of galaxies) is the heart of the Virgo Supercluster, and the galaxy M87M87 (galaxy) is the heavyweight of the Virgo Cluster. The direction towards M87 should be the direction towards the center of the supercluster. What are the supergalactic coördinates of M87?
local m87 = celestia:find("M 87") --one space after M (Messier) celestia:select(m87) local m87Position = m87:getposition() --Convert position from universal frame to supergalacticFrame. m87Position = supergalacticFrame:to(m87Position) --Convert cartesian coordinates to spherical. local longlat = m87Position:getlonglat() local s = string.format( "SGL = %.15g%s\n" .. "SGB = %.15g%s", math.deg(longlat.longitude), std.char.degree, math.deg(longlat.latitude), std.char.degree) SGL = 102.880597309482° SGB = -2.34997614192947°The gas tail of a comet always points away from the Sun, regardless of the comet’s direction of motion. Let’s position the observer to see this.
A Celestia comet follows an
elliptical orbit
with the Sun at one focus.
For example,
Halley’s
CometHallay’s Comet, direction of tail of
has the following
orbital elementsorbital elements
in the file
data/comets.ssccomets.ssc (file).
EllipticalOrbit (in .ssc file)
{
Epoch 2449400.5 #1994 Feb 17 00:00UT
Period 75.31589
SemiMajorAxis 17.834144
Eccentricity 0.967143
Inclination 162.262690
AscendingNode 58.420081
ArgOfPericenter 111.332485
MeanAnomaly 38.384264
}
The epochepoch (orbital element) is the time the snapshot was taken, written as a Julian date (tdb). The periodperiod (orbital element) is in Earth years. The semi-major axissemi-major axis (orbital element) for a comet is in astronomical units (linearDistance).
The eccentricityeccentricity (orbital element) is a dimensionless quantitydimensionless quantity with no unit of measurement. It indicates the shape of the ellipse: 0 for a perfect circle, increasing towards 1 as the ellipse gets longer. The following relationship is satisfied by the eccentricity e and the lengths of the semi-major and semi-minor axessemi-minor axis (of ellipse) a and b. We can easily solve it for any one of a, b, or e in terms of the other two. b2 = a2 (1 − e2) The Sun occupies one of the focifocus (of ellipse) of the ellipse. The distance from the center of the ellipse to a focus is ae. If the ellipse is a circle, this distance is zero. The distance from one end of the ellipse to the nearest focus is a − ae = a(1 − e). If the ellipse is a circle, this distance is a.
The shape of the ellipse is easy to visualize: its’s given by the numbers a and b. The orientation of the ellipse in space is much harder. Let’s introduce a piece of terminology to deal with it. The axisaxis (of orbit) of an object’s orbit is a vector perpendicular to the ellipse, pointing from the object’s primary towards the direction from which the orbit is counterclockwise. For example, the axis of the Earth’s orbit around the Sun would be the Y axis of the Sun’s ecliptic frame. For an observer perched on the arrowhead of this vector, the Earth would orbit counterclockwise around the Sun.
The orientation of the ellipse is given by the next three orbital elements, which are angles in degrees. First, the inclinationinclination (orbital element) for a comet is the angle between the plane of the ellipse and the XZ plane of the Sun’s ecliptic frame. More precisely, it is the angle between the axis of the ellipse and the Y axis of the Sun’s ecliptic frame.
Halley spends half of its time south of the XZ plane of the Sun’s
ecliptic frame,
and half north.
The point where it crosses the XZ plane on its way north is called the
ascending nodeascending node (orbital element);
the point on the way south is the
descending nodedescending node.
The
AscendingNode
value in
data/comets.ssc
gives the longitude of this point in the XZ plane,
measured counterclockwise (when viewed from the north)
from the positive X axis.
The
AscendingNode
value is therefore the size of an angle lying in the XZ plane.
The
apoapsisapoapsis (of orbit)
is the point in the orbit farthest from the primary body;
the
periapsisperiapsis (of orbit)
is the point closest to the primary.
Since Halley’s primary is the Sun,
we can also use the terms
aphelionaphelion (of orbit)
and
perihelionperihelion (of orbit).
The
ArgOfPericenterargument of pericenter (orbital element)
value is the longitude of the perihelion in the plane of the orbit,
measured counterclockwise from the meridian of the ascending node.
The
ArgOfPericenter
value is therefore the size of an angle lying in the plane of the orbit.
Since the perihelion and aphelion are on opposite sides of the orbit,
the longitude of the aphelion is
argOfPericenter + 180°.
The mean anomaly will be discussed in broadsideEllipse.
The orbital elements
are placed in the table at the start of the following program,
converted to units that Celx finds congenial.
The
epoch
and
orbitPeriod
are in days,
the length of the axis is in microlightyears,
and the angles are in radians.
To demonstrate that the tail points away from the Sun, we will position the observer on the axis of the orbit and look straight down at the plane of the ellipse. Viewing the ellipse broadside, we will see its true shape without any foreshortening.
The ideal frame of reference for this problem would have its origin at the Sun and its XZ plane in the plane of the ellipse. The X axis would point along the major axis of the ellipse towards the perihelion. The Y axis would be the axis of the orbit. It would normally point north, but ours will point south because Halley’s orbital inclination of 162° is greater than 90°. Look at the bright side: the observer will see the familiar constellations of Ursa MajorUrsa Major and MinorUrsa Minor as he looks through the ellipse. As usual, the Z axis is determined by the other two axes (framesOfReference); it would be parallel to the minor axis of the ellipse.
We will create this ideal
cometFrame
as a rotation of the Sun’s ecliptic frame.
Let’s start with a scenario that’s too good to be true.
If the ellipse lay in the following orientation in the XZ plane of the
Sun’s ecliptic frame,
the necessary rotation would be
0°
(a.k.a.
std.rotation0std.rotation0)
and the
cometFrame
would be the same as the Sun’s ecliptic frame.
But we are not this lucky.
The ellipse actually lies at a crazy orientation in space,
so we will need a nonzero rotation to move the above ellipse
into its real orientation.
The following program builds this rotation
as the product of three simpler rotations.
We saw in
quaternionMultiplication
that a product can be visualized from
left to right or from right to left.
For this rotation,
we recommend the left-to-right interpretation.
Keep in mind that the rotation that positions the ellipse
will be the rotation that will position the
cometFrame.
When we’re done,
the major and minor axes of the ellipse will be the X and Z axes of the
cometFrame.
1.
First,
we rotate the above ellipse counterclockwise
through an angle of
-orbit.argOfPericenter
radians or
–111°
around the Y axis of the Sun’s ecliptic frame.
A negative angle is necessary to get the counterclockwise direction;
see
orientation.
But instead of negating the angle,
we will negate the Y axis.
Our rotations alsways have a nonnegative angle.
2.
Then we rotate the ellipse
through an angle of
-orbit.inclination
radians or
–162°
around the X axis of the Sun’s ecliptic frame.
This raises the top part of the ellipse towards positive Y by
162°
and lowers the much larger bottom part towards negative Y by the same amount.
(Since
162°
is greater than
90°,
the top part will actually start coming down again
and the bottom part will come back up.)
Part of the ellipse is now above the XZ plane and part below.
Despite the rotation,
the ascending and descending nodes remain unmoved on the X axis.
In fact, they are the only points of the ellipse that remain unmoved
during this rotation.
3.
Finally, we apply one more counterclockwise rotation around the Y axis
of the Sun’s ecliptic frame,
through an angle of
-orbit.ascendingNode
radians or
–58°.
The line connecting the ascending and descending nodes remains in the XZ plane,
and still goes through the origin,
but is now
58°
away from the positive X axis.
From our point of view Halley will orbit in the standard direction, counterclockwise. The planets, however, will orbit clockwise, since Halley’s inclination is almost 180°.
--[[
Look down on the plane of Halley's orbit around the Sun as the comet goes
through its perihelion. Demonstrate that the tail points away from the Sun.
The XZ plane of the cometFrame is the plane of the orbit. It lies in the plane
of the window. The Sun, at (0, 0, 0) in the cometFrame, is at the center of the
window. The X axis of the cometFrame (the major axis of the ellipse) points
towards the top of the window, with the perihelion (a - ae, 0, 0) above the Sun.
Most of the orbit is below the window, out of sight.
The Y axis of the cometFrame points out of the window towards the user.
The Z axis of the cometFrame points towards the right.
The comet orbits counterclockwise from our point of view. The visible part of
the orbit goes from right to left.
]]
require("std")
local orbit = { --from data/comets.ssc file
epoch = 2449400.5, --1994 Feb 17 00:00UT
period = 75.31589 * celestia:find("Sol/Earth"):getinfo().orbitPeriod,
semiMajorAxis = 17.834144 * 1e6 / std.auPerLy, --microlightyears
eccentricity = 0.967143,
inclination = math.rad(162.262690), --at epoch
ascendingNode = math.rad(58.420081), --at epoch
argOfPericenter = math.rad(111.332485), --at epoch
meanAnomaly = math.rad(38.384264) --at epoch
}
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "grid") --distracting
celestia:show("orbits")
--We know that Halley's Comet is Halley's Comet.
celestia:hidelabel("comets")
--Show Halley's orbit when selected, but no other orbits.
celestia:setorbitflagsCelestia:setorbitflags({Planet = false})
local comet = celestia:find("Sol/Halley")
celestia:select(comet)
local info = comet:getinfo()
local rotation =
celestia:newrotation(-std.yaxis, orbit.argOfPericenter)
* celestia:newrotation(-std.xaxis, orbit.inclination)
* celestia:newrotation(-std.yaxis, orbit.ascendingNode)
local cometFrame = celestia:newframe("ecliptic", info.parent, rotation)
observer:setframe(cometFrame)
local a = orbit.semiMajorAxis
local e = orbit.eccentricity
local perihelion = a * (1 - e) --distance in microlightyears from Sun
--Close enough to see tail, far enough to see shape of ellipse.
local observerPosition = celestia:newposition(0, 4 * perihelion, 0)
observer:setposition(cometFrame:from(observerPosition))
--Look towards the Sun. The X axis of the cometFrame (which lies along
--the major axis) points towards the top of the window.
observer:lookat(
cometFrame:from(std.position0),
cometFrame:from(std.xaxis))
--80 days before the perihelion of 1986
celestia:settime(celestia:utctotdb(1986, 2, 9) - 80)
--[[
One orbit of simulation time (75 years) per hour of real time.
The interesting part of the program will take about 20 seconds of
real time. info.orbitPeriod is in Earth days.
]]
celestia:settimescale(24 * info.orbitPeriod)
wait()
end
main()
Pause the above program with the space bar. Then use the straight edge of a piece of paper to verify that the tail points away from the Sun. Better yet, use OpenGL (equalArea) to draw a straight line from the Sun to the nucleus of the comet.
Each celestial object has its own equatorial frame of reference. The object is called the reference object of the frame. The origin of the frame is the center of the reference object. The XZ plane is the plane of the object’s equator, with the X axis pointing towards the object’s vernal equinox. The X axis therefore also lies in the plane of the object’s orbit around its primary. The Y axis points along the axis of the reference object, north for most objects and south for Venus and the other retrograde rotators. The Z axis is determined by the other two axes because all Celestia frames are right-handedright-handed frame; see framesOfReference.
At noon UTC on January 1, 2000, the axes of the Earth’s equatorial frame were parallel to those of the J2000 equatorial coördinates in j2000Equatorial. The X axis of the Earth’s equatorial frame pointed towards RA 0h Dec 0°, the vernal equinox in Pisces. The Y axis pointed towards the north celestial pole near Polaris. But since that moment of alignment, the Earth’s equatorial frame has been gradually tilting as the Earth precessesprecession of Earth’s axis (wobbles on its axis).
In eclipticFrame, we looked along the X axis of the Earth’s ecliptic frame. Let us now look along the X axis of the equatorial frame. We will see the Earth in front of the vernal equinox in Pisces.
--[[
Demonstrate that the X axis of the Earth's equatorial frame currently points
towards Pisces, the Y axis towards Polaris.
Position the observer on the negative X axis and look towards the origin,
with the Y axis pointing up.
]]
require("std")
local function main()
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
local equatorialFrame = celestia:newframe("equatorial", earth)
observer:setframe(equatorialFrame)
local microlightyears = 12 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
observer:setposition(equatorialFrame:from(position))
observer:lookat(
equatorialFrame:from(std.position0),
equatorialFrame:from(std.yaxis))
wait()
end
main()
Change the above program to sight along the Y axis
of the Earth’s equatorial frame.
You will have to select a different up vector;
a reasonable choice would be
equatorialFrame:from(std.zaxis).
A dazzling Antarctica will present itself,
with the Earth blocking our view of the
north
celestial pole.
Now use Venus instead of the Earth. The Universe behind the planet should be upside down, with Venus blocking a point near the south celestial pole.
Sight along the Y axis of the Earth’s equatorial frame again, facing Antarctica and Polaris. View the Earth from 25 radii away, so it doesn’t block as much of the sky. Turn on the ecliptic grid.
celestia:hide("grid") --centered at Polaris celestia:show("eclipticgrid") --centered at Draco
Now speed up time by a factor of ten billion
= 1 · 1010.
Press
l
(lowercase L) ten times,
or call
Observe that the north celestial pole, as marked by the Earth, circles the north pole of the ecliptic in Draco. This gradual change in the direction of the Earth’s axis is called precession.
Select the star ThubanThuban (star) (α Draconis) and start again at the present. This time go backwards with a negative timescale, or by pressing j before the lowercase L’s. When did the Earth’s equatorial frame Y axis point closest to this star?
Start again at the present. Sight along the X axis of the Earth’s equatorial frame towards Pisces, with the Y axis of the Earth’s equatorial frame pointing up. Set the timescale to 10 billion. The target towards which the X axis is pointing will move from left to right along the ecliptic, passing through the 12 constellations of the zodiaczodiac in reverse order. The X axis will spend an entire age in each constellation because the precession is so slow. We have just about completed our traversal of PiscesPisces, Age of, so this is the dawning of the Age of AquariusAquarius, Age of. How long will it take for the X axis to go all the way around the ecliptic?
Let’s find the current tilt (or
obliquityobliquity of Earth’s axis)
of the Earth’s axis
with respect to the axis of the ecliptic.
The two vectors in the following fragment
are unit vectors in universal coördinates.
toDraco
points north along the axis of the ecliptic,
towards
Draco.
toPolaris
points north along the axis of the Earth,
towards
Polaris.
Similarly,
we can show that the tilt of Venus’s axis is
178.761°.
Since the tilt is greater than
90°,
we say that the planet’s rotation is
retrograderetrograde rotation.
Let’s find all the retrograde rotators in the Solar System.
For the iterator
Object:family
and the
string:sub
method,
see
Recursion
--[[
List the solar system objects with retrograde rotation. These are the objects
whose equatorial frame Y axis is more than 90 degrees from the universal frame Y
axis.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
local s = ""
for level, object in celestia:find("Sol"):familyObject:family() do
local equatorialFrame = celestia:newframe("equatorial", object)
local rotationAxis = equatorialFrame:from(std.yaxis)
local theta = math.deg(std.yaxis:angle(rotationAxis))
if theta > 90 then
s = s .. string.format(
"%s/%s %g%s\n",
object:getinfo().parent:name(), object:name(),
theta, std.char.degree)
end
end
celestia:print(s:substring.sub(1, 2^10 - 1), 60, -1, 1, 1, -1)
wait()
end
main()
Sol/Venus 178.761°
Sol/Uranus 97.722°
Uranus/Miranda 95.1698°
etc.
Neptune/Triton 130.915°
Sol/Pluto 115.6°
etc.
Sol/2 Pallas 113°
etc.
The above program assumed that the plane of each body’s orbit is the XZ plane of the universal frame of reference. In reality, each body has its own orbital plane. We can get more accurate angles by using the –Z axis of each body’s “chase frame” (chaseFrame), which is exactly perpendicular to the body’s orbital plane.
local equatorialFrame = celestia:newframe("equatorial", object) local chaseFrame = celestia:newframe("chase", object) --vectors in universal frame local rotationAxis = equatorialFrame:from(std.yaxis) local orbitAxis = chaseFrame:from(-std.zaxis) local theta = math.deg(orbitAxis:angle(rotationAxis)) Sol/Venus 177.362° Sol/Uranus 97.7709° etc.The Earth goes around the Sun at varying speeds, fastest at perihelion in January and slowest at aphelion in July. This causes the Sun as seen from the Earth to move along the ecliptic at varying speeds, fastest in January and slowest in July. And even if the Sun moved steadily, it would still change its right ascension at varying speeds because of the tilt of the ecliptic: fastest at the solstices and slowest at the equinoxes. (Imagine a flight from New York to London along a great circle. The plane would cross the meridians of longitude most frequently during the northernmost part of the flight.) These two effects cancel out on approximately June 14th of every year.
We can gauge the Sun’s uneven progress along the ecliptic by comparing it with an imaginary mean Sunmean Sun. This fictitious body moves sedately along the celestial equator, increasing its right ascension at the constant rate of 360° per year. The following program keeps the observer on the Earth’s sub-mean solar pointsub-mean solar point, the point on the Earth’s surface where the mean Sun is directly overhead. This point is always on the Earth’s equator.
The observer looks straight up into the sky towards the mean Sun, keeping it at the center of the window. Polaris is off the top of the window. The real Sun appears to the left (east) or right (west) of the mean Sun, depending on whether the real Sun is ahead of or behind the mean Sun in right ascension. The real Sun also appears above (north) or below (south) the mean Sun, depending on the season of the year. These changing offsets with respect to the mean Sun combine to make the real Sun trace a figure eight called the analemma.
The horizontal component of the analemma indicates how fast or slow a sundial would be on each day of the year. When the real Sun is slow in its journey along the ecliptic (i.e., to the right [west] of the mean Sun), the sundial is fast because the real Sun arrives earlier than the mean Sun at any given position in their east-to-west journey across the daytime sky. When the real sun is fast, the sundial is slow.
The ideal frame of reference for this problem would have
its origin at the center of the Earth
and its XZ plane in the plane of the equator of the Earth.
The X axis would point towards the mean Sun,
not the real Sun,
and the Y axis towards Polaris.
We will create this
meanSolFrame
with a
rotation
that rotates the
toMeanSol
vector at the constant rate of
360°
per year.
This vector will be the X axis of the
meanSolFrame.
For now, we will just watch the real Sun zigzag around. We will draw the figure eight of the analemma on the window using the OpenGL graphics in Corkscrew, and we will create the analemma without a tick handler in scriptedRotation.
--[[
Move the Sun along the figure eight of the analemma,
as seen from the sub-mean solar point on the Earth.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local equatorialFrame = celestia:newframe("equatorial", earth)
local info = earth:getinfo()
local orbitPeriod = info.orbitPeriod
local microlightyears =
(earth:radius() + info.atmosphereHeight) / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
--Assume that the Sun and the man Sun agree in right ascension on the starting
--date (June 14), i.e., assume that the value of the equation of time is 0 then.
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
local t0 = celestia:utctotdb(year, 6, 14)
local toSol0 = equatorialFrame:to(sol:getposition(t0), t0):tovector()
local toMeanSol0 = std.yaxis:erect(toSol0):normalize()
local function tickHandler()
local t = celestia:gettime()
local years = (t - t0) / orbitPeriod --years since t0
local rotation = celestia:newrotation(std.yaxis, -2 * math.pi * years)
local toMeanSol = rotation:transform(toMeanSol0)
local right = toMeanSol --X axis of meanSolFrame points towards mean Sun
local up = std.yaxis --Y axis of meanSolFrame points to Polaris
local forward = up ^ right
local meanSolFrame = celestia:newframe("equatorial", earth,
celestia:newrotationforwardup(forward, up))
observer:setframe(meanSolFrame)
observer:setposition(meanSolFrame:from(position))
observer:lookat(
meanSolFrame:from(2 * position), --Look away from the origin.
meanSolFrame:from(std.yaxis))
--359 degrees should be treated as -1 degree.
local solPosition = meanSolFrame:to(sol:getposition())
local degreesOfArc = math.deg(solPosition:getlonglat().longitude)
if degreesOfArc >= 180 then
degreesOfArc = degreesOfArc - 360
end
local speed = ""
if degreesOfArc > 0 then
speed = std.char.larr .. " Sun fast, sundial slow"
elseif degreesOfArc < 0 then
speed = "Sun slow, sundial fast " .. std.char.rarr
end
local minutesOfTime = math.absmath.abs(degreesOfArc) * 24 * 60 / 360
local minutes = math.floormath.floor(minutesOfTime) --integer part
local seconds = 60 * math.fmodmath.fmod(minutesOfTime, 1) --fractional part
local n = 10 --how many MMs to print above and below center
local mm = "MM\n"
local utc = celestia:tdbtoutc(t)
local s = string.format(
"%s"
.. "MM %s %d, %d\n"
.. "MM %s\n"
.. "MM %d minutes, %d seconds\n"
.. "%s",
mm:repstring.rep(n - 1),
std.monthName[utc.month], utc.day, utc.year,
speed, minutes, std.round(seconds),
mm:rep(n - 1))
celestia:print(s, 1, 0, 0, -1, n)
end
local function main()
celestia:select(sol)
--tall enough to see top and bottom of analemma, plus 1-degree margin
observer:setfov(2 * (std.tilt + math.rad(1)))
celestia:settime(t0)
--Ten days of simulation time per second of real time.
celestia:settimescale(60 * 60 * 24 * 10)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
MM June 14, 2013
MM
MM 0 minutes, 0 seconds
The equation of timeequation of time is a function giving the horizontal component of the analemma for a given date. Its value is positive when the real Sun is to the right of the mean Sun; the real Sun is then slow and the sundial is fast. Its value is negative when the real Sun is to the left of the mean Sun; the real Sun is then fast and the sundial is slow.
Let’s plot the graph of the equation for the current year.
We assume that the value of the function is zero at midnight on June 14.
Don’t forget the
LuaHook
parameter in
celestia.cfg
(luaHookFunctions).
--[[
This file is luahook.celx.
Draw the equation of time for the current year.
January 1 is at the left edge of the window, December 31 is at the right.
The top edge is when a sundial is 18 minutes fast, bottom edge 18 minutes slow.
]]
--variables used by equationOfTime:
local sol = nil --Celestia can't call celestia:find at this early time.
local earth = nil
local orbitPeriod = nil
local equatorialFrame = nil
--Return a positive number if a sundial is fast on date t, negative if slow.
--Return value is in days, not minutes.
local function equationOfTime(t)
assert(type(t) == "number")
if sol == nil then
sol = celestia:find("Sol")
earth = celestia:find("Sol/Earth")
orbitPeriod = earth:getinfo().orbitPeriod
equatorialFrame = celestia:newframe("equatorial", earth)
end
local year = celestia:tdbtoutc(t).year --current year
local t0 = celestia:utctotdb(year, 6, 14)
local toSol0 = equatorialFrame:to(sol:getposition(t0), t0):tovector()
local toMeanSol0 = std.yaxis:erect(toSol0):normalize()
local years = (t - t0) / orbitPeriod --years since t0
local rotation = celestia:newrotation(std.yaxis, -2 * math.pi * years)
local toMeanSol = rotation:transform(toMeanSol0)
local meanSolFrame = celestia:newframe("equatorial", earth,
celestia:newrotationforwardup(std.yaxis ^ toMeanSol, std.yaxis))
local solPosition = meanSolFrame:to(sol:getposition(t), t)
local theta = solPosition:getlonglat().longitude
if theta >= math.pi then
theta = theta - 2 * math.pi
end
--theta is how fast the real Sun is. Convert radians to days.
--Negate it to return how fast the sundial is.
return -theta / (2 * math.pi)
end
celestia:setluahook {
year = nil,
lengthOfYear = nil,
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
self.year = celestia:tdbtoutc(celestia:gettime()).year
self.lengthOfYear =
celestia:utctotdb(self.year + 1, 1, 1)
- celestia:utctotdb(self.year, 1, 1)
end
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
local width, height = celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
--origin at center of left edge of window
gl.Translate(0, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING)
gl.Disable(gl.TEXTURE_2D) --disabled for graphics
if celestia:getrenderflags().smoothlines then
gl.Enable(gl.LINE_SMOOTH) --antialiasing
gl.LineWidth(1.5)
end
gl.Color(1, 1, 1, 1) --rgba
gl.Begin(gl.LINE_STRIPgl.LINE_STRIP)
--left to right across the pixels of the window
for x = 0, width - 1 do
local t = celestia:utctotdb(self.year, 1, 1)
+ self.lengthOfYear * x / (width - 1)
local minutesOfTime = equationOfTime(t) * 24 * 60
--sundial fast or slow by at most 16 or 17 minutes
local y = (height / 2) * (minutesOfTime / 18)
gl.Vertex(x, y)
end
gl.End()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
end
}
--[[
Provide a black background for the graph of the equation of time,
with a horizontal red X axis.
]]
require("std")
local function main()
celestia:sane()
--Render only the ecliptic. It will be the X axis of the graph.
local flags = celestia:getrenderflags()
for key, value in pairs(flags) do
flags[key] = key ==== (equals operator) "ecliptic" --true if key equals "ecliptic"
end
celestia:setrenderflags(flags)
flags = celestia:getlabelflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setlabelflags(flags)
wait()
end
main()
Add bells and whistles:
margins on the left and right with
glu.Ortho2Dglu.Ortho2D,
X and Y axes with labeled ticks,
and a graph paper background in a subdued color.
Use the
std.zero
function
(findZero)
to find the zeroes, maxima, and minima,
and label them with ticks.
Can you plot the separate contributions to the equation of time
of the eccentricity of the Earth’s orbit
and the tilt of the Earth’s axis?
Does Mars have an equation of time?
Let’s watch a satellite going around its orbit.
We’ll pick
NeptuneNeptune’s
moon
NereidNereid (moon of Neptune),
whose plain vanilla
EllipticalOrbit
has an
eccentricity
large enough for a well-proportioned ellipse
with attractive variations in speed.
The following are Nereid’s
orbital elements
in the file
data/solarsys.sscsolarsys.ssc (file).
The orbital elements are placed in the table at the start of the following program, converted to units that Celx finds congenial. Since Nereid is a moon, not a comet, the period is in days and the angles are measured with respect to the equatorial frame of the primary. For the mean anomaly, see the exercises below. For the other values, and their rôles in creating the new frame, see tailPoints.
The ellipse of Nereid’s orbit will lie flat in the plane of the window, with the major axis horizontal because the window is landscape. We will look down at Nereid’s orbit from above, peering through the ellipse towards the south pole of the ecliptic in Dorado. The orbit will also lasso other southern landmarks such as the Large Magellanic CloudLarge Magellanic Cloud and CanopusCanopus (star). The observer will be positioned on the line perpendicular to, and going through the center of, the ellipse. He will view the orbit broadside, seeing its true shape with no foreshortening.
In
tailPoints
we created a
cometFrame
as a rotation of the Suns’s ecliptic frame.
Here we will create a
nereidFrame
as a rotation of Neptune’s equatorial frame.
The origin of the
nereidFrame
will be the center of Neptune,
and its XZ plane will be the plane of Nereid’s orbit.
The X axis will point along the major axis of the ellipse towards the periapsis.
The Y axis will be perpendicular to the plane of the orbit,
pointing north since Nereid’s orbit is not retrograde.
As usual,
the Z axis will be determined by the other two axes
(framesOfReference);
it will be parallel to the minor axis of the ellipse.
Neptune will be at
(0, 0, 0)
in the
nereidFrame.
The center of the ellipse will be at
(–ae, 0, 0),
where
a
is the length of the semi-major axis
and
e
is the eccentricity;
see
tailPoints
for a diagram.
The periapsis will be
(a − ae, 0, 0),
the apoapsis will be
(–a − ae, 0, 0),
and the observer will be at
(–ae, 3a, 0).
The center of the ellipse will be at the center of the window.
The X axis will point right,
the Z axis will point down,
and the Y axis will point out of the screen towards the observer.
--[[
Display an overhead view of Nereid's orbit around Neptune. The observer is on
a line perpendicular to, and going through the center of, the ellipse.
Neptune is at the right focus, with the periapsis to the right of it.
]]
require("std")
local orbit = { --from data/solarsys.ssc file
epoch = 2447763.5, --1989 Aug 25 00:00UT (VoyagerVoyager 2 (spacecraft) encounter)
period = 360.13619, --mean, in days
semiMajorAxis = 5513400 / KM_PER_MICROLY, --mean
eccentricity = 0.7512, --mean
inclination = math.rad(28.385), --at epoch
ascendingNode = math.rad(190.678), --at epoch
argOfPericenter = math.rad(17.690), --at epoch
meanAnomaly = math.rad(36.056) --at epoch
}
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "grid") --distracting lines
celestia:show("orbits")
--Show the orbits of only Nereid and TritonTriton (moon of Neptune).
celestia:setorbitflagsCelestia:setorbitflags({Planet = false})
local nereid = celestia:find("Sol/Neptune/Nereid")
celestia:select(nereid)
local info = nereid:getinfo()
local rotation =
celestia:newrotation(-std.yaxis, orbit.argOfPericenter)
* celestia:newrotation(-std.xaxis, orbit.inclination)
* celestia:newrotation(-std.yaxis, orbit.ascendingNode)
local nereidFrame =
celestia:newframe("equatorial", info.parent, rotation)
observer:setframe(nereidFrame)
local a = orbit.semiMajorAxis
local e = orbit.eccentricity
local centerOfEllipse = celestia:newposition(-a * e, 0, 0)
local observerPosition = celestia:newposition(-a * e, 3 * a, 0)
observer:setposition(nereidFrame:from(observerPosition))
--major axis horizontal, minor axis vertical for landscape window
local up = nereidFrame:from(-std.zaxis)
observer:lookat(nereidFrame:from(centerOfEllipse), up)
celestia:settime(orbit.epoch)
--one simulation orbit per 30 seconds of real time
celestia:settimescale(60 * 60 * 24 * info.orbitPeriod / 30)
wait()
end
main()
In equalArea we will overlay the picture with line segments illustrating Kepler’s Equal Area Law.
The mean anomalymean anomaly (orbital element) is the fraction of the orbital period that has elapsed since the satellite was most recently at its periapsis. Strangely, it is usually expressed as an angle of 0 to almost 360° even though it is a fraction of an interval of time, not a fraction of a circle. Since we are programming in Celx, we will write it as 0 to almost 2π radians. The mean anomaly in the above table is measured in radians at the time of the epoch.
Let’s use the mean anomaly to display Nereid
at the periapsis before the epoch.
At periapsis, Nereid is on the positive X axis of the
nereidFrame,
which points to the observer’s right.
Change the above
Celestia:settime
and
Celestia:settimescale
to the following.
The expression
orbit.meanAnomaly / (2 * math.pi)
is a fraction in the range 0 to almost 1.
It is the fraction of the orbital period that elapsed
between the periapsis before the epoch and the epoch.
Let’s compute the mean anomaly at the epoch ourselves,
instead of reading it from
data/solarsys.ssc.
This will be more than a foray into Keplerian Astronomy—it will be a
reconnaissance-in-force requiring new terminology.
The
radius vector
is the line connecting a primary with its satellite.
And the
eccentric
anomalyeccentric anomaly
is a convenient intermediate result,
from which we will eventually compute
Nereid’s
current position.
Here we will demonstrate its usefulness
by computing the mean anomaly at the epoch.
The following relationship is satisfied by the length of the radius vector r, the semi-major axis a, the eccentricity e, and the eccentric anomaly E. r = a(1 − e cos E) We can solve this equation for cos E, cos E = 1 − r/a e and then for E: E = arccosarccosine (trig function) 1 − r/a e The mean anomaly M is then given by Kepler’s equationKepler’s Equation M = E − e sin E
celestia:settime(orbit.epoch) local r = nereidFrame:to(satellite:getposition()):tovector():length() local E = math.acosmath.acos((1 - r / orbit.semiMajorAxis) / orbit.eccentricity)
local M = E - orbit.eccentricity * math.sin(E) --Kepler's equation
local s = string.format("Mean anomaly at epoch: %g%s",
math.deg(M), std.char.degree)
The output agrees with the value
36.056°
in
data/solarsys.ssc.
Now let’s compute the x, y, z position of Nereid at any given time. Of course, Celestia already does this for us. But we will demonstrate that we can do it ourselves using the orbital elements.
If we had the current eccentric anomaly
E,
we could easily compute the polar coördinates
(r, θ)
of the satellite in the
nereidFrame
XZ plane.
In fact, we’ve already seen how to compute
r,
r = a(1 − e cos E)
and there’s another formula for
θ.
We could then convert the polar coördinates
to Cartesian coördinates in the XZ plane,
and finally to Cartesian coördinates in the universal frame.
The problem is getting the eccentric anomaly. We can start by computing the mean anomaly M from the current time t. M = 2π t − epoch period And from Kepler’s equation we know that E = M + e sin E There is no simple way, however, to solve Kepler’s equation for E. The application MathematicaMathematica (application) commented dryly that “The equations appear to involve the variables to be solved for in an essentially non-algebraic way.”
But we don’t have to solve for E. We can just compute a series E0, E1, E2, … of increasingly accurate approximations to E. Our first approximation E0 can simply be M because the eccentricity and the sine are both is fairly small (less than or equal to 1 in absolute value).
E0 = M
--[[
Display an overhead view of Nereid's orbit around Neptune. The observer is on
a line perpendicular to, and going through the center of, the ellipse.
Neptune is at the right focus, with the periapsis to the right of it.
Compute the current position of Nereid from its orbital elements,
and compare it to the position computed by Celestia.
]]
require("std")
local orbit = {
epoch = 2447763.5, --1989 Aug 25 00:00UT (Voyager encounter)
period = 360.13619, --mean, in days
semiMajorAxis = 5513400 / KM_PER_MICROLY, --mean
eccentricity = 0.7512, --mean
inclination = math.rad(28.385), --at epoch
ascendingNode = math.rad(190.678), --at epoch
argOfPericenter = math.rad(17.690), --at epoch
meanAnomaly = math.rad(36.056) --at epoch
}
--variables used by tickHandler:
--time of periapsis before epoch (or epoch itself if that was the periapsis)
local t0 = orbit.epoch - orbit.period * orbit.meanAnomaly / (2 * math.pi)
local a = orbit.semiMajorAxis
local e = orbit.eccentricity
assert(e ~= 1) --so the tickHandler can divide by 1-e
local nereid = celestia:find("Sol/Neptune/Nereid")
local name = nereid:name()
local parent = nereid:getinfo().parent
local equatorialFrame = celestia:newframe("equatorial", parent)
local nereidFrame = celestia:newframe("equatorial", parent,
celestia:newrotation(-std.yaxis, orbit.argOfPericenter)
* celestia:newrotation(-std.xaxis, orbit.inclination)
* celestia:newrotation(-std.yaxis, orbit.ascendingNode)
)
local function tickHandler()
local position = nereid:getposition()
local s = string.format("%s's position computed by Celestia:\n"
.. "Universal frame: (%g, %g, %g)\n",
name, position:getxyz())
s = s .. string.format(
"%s equatorial frame: (%g, %g, %g)\n",
parent:name(), equatorialFrame:to(position):getxyz())
local p = nereidFrame:to(position)
s = s .. string.format("nereidFrame: (%g, %g, %g)\n", p:getxyz())
local longlat = p:getlonglat()
s = s .. string.format(
"Polar co%srdinates in nereidFrame XZ plane: (%g, %g%s)\n\n",
std.char.ouml,
longlat.distance,
math.deg(longlat.longitude),
std.char.degree)
--Current mean anomaly.
local M = 2 * math.pi * (celestia:gettime() - t0) / orbit.period
--Approximate the current eccentric anomaly.
local E = M
for i = 1, 10 do
E = M + e * math.sin(E)
end
--Polar coordinates (r, theta) of nereid in nereidFrame XZ plane.
--r is the length of the radius vector.
--theta is called the "true anomaly".
local r = a * (1 - e * math.cos(E))
local theta = 2 * math.atanmath.atan(
math.sqrt((1 + e) / (1 - e)) * math.tanmath.tan(E / 2))
--[[
Cartesian coordinates of Nereid in nereidFrame in microlightyears.
In the customary XY plane, the Y axis points up.
In the XZ plane, the Z axis points down.
That's why we have to negate the z coordinate.
]]
local nereidFrameComputed = celestia:newposition(
r * math.cos(theta),
0,
-r * math.sin(theta))
local universalFrameComputed = nereidFrame:from(nereidFrameComputed)
local equatorialFrameComputed =
equatorialFrame:to(universalFrameComputed)
s = s .. string.format("%s's position computed by Celx program:\n"
.. "Universal frame: (%g, %g, %g)\n",
name, universalFrameComputed:getxyz())
s = s .. string.format(
"%s equatorial frame: (%g, %g, %g)\n",
parent:name(), equatorialFrameComputed:getxyz())
s = s .. string.format("nereidFrame: (%g, %g, %g)\n",
nereidFrameComputed:getxyz())
s = s .. string.format(
"Polar co%srdinates in nereidFrame XZ plane: (%g, %g%s)\n\n",
std.char.ouml, r, math.deg(theta), std.char.degree)
local kilometers = position:distanceto(universalFrameComputed)
s = s .. string.format("Error: %g kilometers = %g microlightyears",
kilometers, kilometers / KM_PER_MICROLY)
celestia:print(s, 1, -1, 1, 1, -6)
end
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "grid") --distracting lines
celestia:show("orbits")
celestia:select(nereid)
celestia:setorbitflags({Planet = false})
local centerOfEllipse = celestia:newposition(-a * e, 0, 0)
local observerPosition = celestia:newposition(-a * e, 3 * a, 0)
observer:setframe(nereidFrame)
observer:setposition(nereidFrame:from(observerPosition))
--major axis horizontal, minor axis vertical for landscape window
local up = nereidFrame:from(-std.zaxis)
observer:lookat(nereidFrame:from(centerOfEllipse), up)
celestia:settime(t0)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Press j, k, l
to control the timescale,
and space bar to pause the program.
At the periapsis before the epoch,
Nereid was on the
nereidFrame
X axis:
Keep track of the maximum error as Nereid goes all the way around its orbit.
Can we make the error smaller by using a more accurate estimate of the
eccentric anomaly?
One way to do this would be to increase the
for
loop to 20 iterations.
If the loop now takes too much time,
use a smarter algorithm that converges more rapidly:
What effect does this have on the maximum error?
The alternative algorithms implemented by the
for
loop are taken from the source code of Celestia.
Read them there.
The arithmetic is written in the structures
SolveKeplerFunc1
and
SolveKeplerFunc2
in
version/src/celengine/orbit.cpp.
The
for
loop that they share is written once and for all in the template function
solve_iteration_fixed
in
version/src/celmath/solve.h.
Look at other orbits of handsome eccentricity,
e.g.,
that of
Sol/Saturn/Bestla.
For an extreme eccentricity of 0.967143,
try
Halley’s
Comet.
Its
Period
in
data/comets.ssc
is in Earth years;
multiply it by
celestia:find("Sol/Earth"):getinfo().orbitPeriod
to convert it to days.
The
SemiMajorAxis
in
data/comets.ssc
is in astronomical units;
multiply it by
1e6 / std.auPerLy
to convert it to microlightyears.
The angles are in the universal frame.
This means that the rotated frame
should be a rotation of the Sun’s ecliptic frame,
not the Sun’s equatorial frame.
The annual
Perseid meteor showerPerseid meteor shower
is composed of debris that follow the orbit of
comet Swift-TuttleSwift-Tuttle (comet).
Let’s verify that the Earth crosses the plane of the comet’s orbit
each year on August 12th.
Add the comet to the
data/comets.ssc
file and restart Celestia.
In the
main
function,
show the orbits of the planets and the comet.
See
renderFlags.
Change the name of the rotated frame from
nereidFrame
to
swiftFrame.
The comet’s orbit lies in the XZ plane of the
swiftFrame.
Give the observer an edge-on view of the orbit.
Now set the time to August 12th of the current year.
local year = celestia:tdbtoutc(celestia:gettime()).year celestia:settime(celestia:utctotdb(year, 8, 12)) celestia:settimescale(1)Is the Earth passing through the plane of the comet’s orbit? Is there any danger?
Each celestial object has its own bodyfixed frame. (The old name planetographic is now deprecated.) The object is called the reference object of the frame. The origin of the frame is the center of the reference object and the XZ plane is the plane of the object’s equator. The X axis pierces the object’s surface at latitude 0° North, longitude 0° East. For the Earth, this point is in the Gulf of Guinea off the west coast of Africa. The Z axis pierces the surface at latitude 0° North, longitude 90° West. For the Earth, this is in the Galápagos Islands off the west coast of South America. The Y axis pierces the surface at the north pole of the object.
For retrograde rotators such as Venus, the Y axis pierces the surface at the south pole of the object. To keep the axes right-handed (framesOfReference) in this case, the Z axis has to pierce the surface at latitude 0° North, longitude 90° East.
Looking down at the Earth’s bodyfixed XZ plane from the north pole, the Y axis points straight towards us and is invisible:
In eclipticFrame, we looked along the X axis of the Earth’s ecliptic frame. In equatorialFrame, we looked along the X axis of the Earth’s equatorial frame. Now let’s look along the X axis of the Earth’s bodyfixed frame, with the Y axis pointing up. The bodyfixed axes are displayed as colored arrows by the following program. The red “X” arrow does indeed point along the Earth’s bodyfixed X axis. But the blue “Z” arrow points along the positive Y axis, and the green “Y” arrow points along the negative Z axis.
--[[
Position the observer on the negative X axis of the Earth's bodyfixed frame,
looking towards the origin with the Y axis pointing up.
Keep him in geostationary orbit above the Marshall Islands in the Pacific
(latitude 0 degrees North, longitude 180 degrees East).
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("cloudmaps", "cloudshadows") --distracting
local earth = celestia:find("Sol/Earth")
earth:addreferencemark({type = "body axes"})
earth:addreferencemark({type = "planetographic grid"})
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
local microlightyears = 12 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
observer:setposition(bodyfixedFrame:from(position))
observer:lookat(
bodyfixedFrame:from(std.position0),
bodyfixedFrame:from(std.yaxis))
wait()
end
main()
Run the program and fast forward with the keystrokes j, k, l.
Since we have
setframed
the observer,
he will adhere to the bodyfixed frame
and remain above the
Marshall Islands
as the rest of the Universe rotates in the background.
Change
"Sol/Earth"
to
"Sol/Venus"
in the above program.
Observe that the universe behind the planet is now upside down.
Do
"Sol/Earth/Hubble"
and
"Sol/Cassini"
have a bodyfixed frame?
Read the program in celestialSphere that keeps the observer fixed above the point at 0° North 0° East.
The terminatorterminator is the line on the surface of a planet that separates day from night. Let’s watch Mercury’s terminator hesitate at the meridian of 90° West. The observer is positioned on the bodyfixed positive Z axis, above the point where it pierces the equator at 90° W. The X axis points to the right, the Y axis points up and the Z axis points out of the window towards the user.
See solarDays for the computation of Mercury’s solar day, and sunsEye for another view of Mercury’s rotation.
--[[
Watch Mercury's terminator hesitate as we hover over the equator
at 90 degrees W.
]]
require("std")
local function main()
local observer = celestia:sane()
local mercury = celestia:find("Sol/Mercury")
celestia:select(mercury)
mercury:addreferencemark({type = "sun direction"})
mercury:addreferencemark({type = "planetographic grid"})
mercury:addreferencemark({ --Show the terminator as a yellow line.
type = "visible region",
target = celestia:find("Sol")
})
local bodyfixedFrame = celestia:newframe("bodyfixed", mercury)
observer:setframe(bodyfixedFrame)
local lat = math.rad(0)
local long = math.rad(-90) --west longitude is negative
local microlightyears = 5 * mercury:radius() / KM_PER_MICROLY
local position = celestia:newpositionlonglat(long, lat, microlightyears)
observer:setposition(bodyfixedFrame:from(position))
--The up vector is Mercury's axis of rotation.
local up = bodyfixedFrame:from(std.yaxis)
observer:lookat(mercury:getposition(), up)
local info = mercury:getinfo()
local orbitPeriod = info.orbitPeriod --in Earth days
local rotationPeriod = info.rotationPeriod --in Earth days
--length of Mercurian solar day in Earth days
assert(orbitPeriod ~= rotationPeriod)
local day =
orbitPeriod * rotationPeriod / (orbitPeriod - rotationPeriod)
--One Mercurian solar day of simulation time
--per 12 seconds of real time.
celestia:settimescale(60 * 60 * 24 * day / 12)
wait()
end
main()
Change the observer’s longitude to 0° or 180° to get a better view of the places where the yellow subsolar vector hesitates. What does it look like from above Mercury’s north pole?
Add the three reference marks with a
for
loop.
The variable
marks
refers to an
array of tables.
Mare MarginisMare Marginis (lunar sea) is at the edge of the hemisphere of the Moon that is visible from the Earth. Watch the edge of the visible region moving back and forth across the mare due to the librationlibration of Moon of the Moon.
celestia:hidelabel("moons") --We know that the Moon is the Moon. celestia:showlabel("locations") --locations on the Moon --enough light to see the mare during the long lunar night celestia:setambientCelestia:setambient(.2)
The line that marks the edge of the visible region should match the color
of the body-to-body vector that points from the Moon towards the Earth.
Get the color from the constructor for class
BodyToBodyDirectionArrow
in
version/src/celengine/axisarrow.cpp.
Position the user above Mare Marginis, three lunar radii from the center of the Moon to be close enough to make the labels visible.
local mare = celestia:find("Sol/Earth/Moon/Mare Marginis") celestia:select(mare) local longlat = bodyfixedFrame:to(mare:getposition()):getlonglat() local microlightyears = 3 * moon:radius() / KM_PER_MICROLY local position = celestia:newpositionlonglat( longlat.longitude, longlat.latitude, microlightyears) observer:setposition(bodyfixedFrame:from(position)) --One sidereal month of simulation time per 12 seconds of real time. local orbitPeriod = moon:getinfo().orbitPeriod --in Earth days celestia:settimescale(60 * 60 * 24 * orbitPeriod / 12)We’ll have another view of lunar libration in Libration.
In the 1950’s, Cambridge University issued a series of catalogs of the radio sources on the celestial sphere. The third catalog was referred to as 3C,3C (Cambridge catalog) and the 273th entry in it was 3C 273. Let’s pinpoint the right ascension and declination of this quasar.
For the times when the Moon covered and uncovered the radio source on August 5, 1962, as seen from the radio telescope at Parkes in Australia, see the bibliography in bibliography. The vectors A and B point from Parkes to the Moon at these two times. We give them uppercase names because we will think of them as points on the celestial sphere; see the following diagram. The circles are the limbs (outlines) of the Moon at the two times. The points we want to find are C and D. Point E is the intersection of line c with the limb of the first Moon. Point O, not shown in the diagram, is the center of the Earth and of the celestial sphere. It is located right between the reader’s eyes.
The sides of the triangles are great circlesgreat circle on the celestial sphere, so their lengths can be represented in degrees or radians of arc. For example, the length of side c can be represented as the angle AOB. The following formula will use lowercase letters for the size of angles whose vertex is the center of the celestial sphere, and uppercase for angles whose vertex is on the surface of the sphere. For example, c is the size of angle AOB and C is the size of angle ACB.
We already know the lengths of the sides of the triangle. The spherical law of cosinesspherical law of cosines will give us the size of the angle A.
cos a = cos b cos c + sin b sin c cos AWe can solve it for cos A
cos A = cos a − cos b cos c sin b sin c and then for A itself: A = arcsin cos a − cos b cos c sin b sin c
In the following program,
the vectors
A
and
B
have been renamed
toMoon[1]
and
toMoon[2]
respectively,
since it is easier to loop through them if they are array elements.
The angles
b
and
a
have been renamed
radius[1]
and
radius[2]
respectively,
and are measured in radians.
Point
E
has been renamed
toLimb.
The first call to
Rotation:transform
(transformVector)
rotates point
A
(a.k.a.
toMoon[1])
through an angle of b
(a.k.a.
radius[1])
to create point
E
(a.k.a.
toLimb).
The second and third calls to
transform
rotate point
E
along the limb of the first Moon through an angle of positive and negative
A
radians;
we try both signs with a
for
loop.
These rotations get us to the desired points
C
and
D.
--[[
Display the Right Ascension and Declination of the two points that were on the
limb of the Moon as seen from the Parkes Observatory at both of the two given
times. These points are the possible locations of quasar 3C 273.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:settimescale(0)
local earth = celestia:find("Sol/Earth")
local moon = celestia:find("Sol/Earth/Moon")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
--Parkes Observatory, New South Wales, Australia
local position = celestia:newpositionlonglat(
math.rad( 148 + (15 + 44.3 / 60) / 60),
math.rad(-( 32 + (59 + 59.8 / 60) / 60)),
(earth:radius() + .324) / KM_PER_MICROLY)
observer:setposition(bodyfixedFrame:from(position))
local t = {
celestia:utctotdb(1962, 8, 5, 7, 46, 0.0), --Moon covers 3C 273
celestia:utctotdb(1962, 8, 5, 9, 5, 45.5) --Moon uncovers 3C 273
}
local toMoon = {} --vectors from Parkes to Moon
local radius = {} --angular radii of Moon as seen from Parkes
for i = 1, #t do
celestia:settime(t[i])
toMoon[i] = moon:getposition() - observer:getposition()
local moonDistance = toMoon[i]:length() * KM_PER_MICROLY
radius[i] = math.asin(moon:radius() / moonDistance)
end
local axis = toMoon[2] ^ toMoon[1]
assert(axis:length() > 0)
local rotation = celestia:newrotation(axis:normalize(), radius[1])
local toLimb = rotation:transform(toMoon[1])
--angle A derived from spherical law of cosines
axis = toMoon[1]:normalize()
local c = toMoon[1]:angle(toMoon[2])
local product = math.sin(radius[1]) * math.sin(c)
assert(product > 0)
local A = math.acos(
(math.cos(radius[2]) - math.cos(radius[1]) * math.cos(c))
/ product)
local radecFrame = celestia:newframe("universal", std.radecRotation)
local toQuasar = {}
local s = string.format(
"Actual position of quasar 3C 273:\n"
.. "RA 12h 29m 6.7s Dec 2%s 3%s 9%s\n\n"
.. "Computed positions:\n",
std.char.degree, std.char.minute, std.char.second)
for i, sign in ipairs({1, -1}) do
rotation = celestia:newrotation(sign * axis, A)
toQuasar[i] = rotation:transform(toLimb)
local longlat = radecFrame:to(toQuasar[i]):getlonglat()
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
s = s .. string.format(
"RA %dh %dm %.2gs Dec %s%d%s %d%s %.2g%s\n",
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
end
celestia:mmprint(s, math.huge, -1, 1, 1, -1)
observer:setfovObserver:setfov(3 * radius[2]) --Moon spans 2/3 of height of window
local orientation =
celestia:newrotationforwardup(toQuasar[2], std.yaxis)
--Blink back and forth between the two times.
while true do
for i = 1, #t do
celestia:settime(t[i])
observer:setorientation(orientation)
wait(3)
end
end
end
main()
Actual position of quasar 3C273:
RA 12h 29m 6.7s Dec 2° 3′ 9″
Computed positions:
RA 12h 28m 52s Dec +1° 57′ 4.5″
RA 12h 29m 5.9s Dec +2° 3′ 8.2″
The 64-meter radio telescope at Parkes can tilt down to 60° from the zenith. Read about altitude and azimuth in altazimuthCoordinates and see the Bibliography for the times of the other occultations of 3C 273 by the Moon in 1962. Were any of them at or just below the 60° limit? Is there any truth to the story that chainsaw wielding astrophysicists climbed the scaffolding during the observations and cut off the guard rails to allow the telescope to swing lower?
Let’s rotate the observer around the Earth
in step with the above model of the weather.
We will start at time
t0
at
latitude
0°
North
longitude
0°
Eeast
over the South Atlantic
and keep him over the same cloud.
His motion will be programmed with respect to the Earth’s bodyfixed frame.
--[[
Stay with the clouds as they rotate around the Earth.
Keep the observer over the cloud that was at 0 N 0 E at time t0.
Watch the continents rotate from east to west under the clouds.
]]
require("std")
--variables used by tickHandler:
local t0 = celestia:gettime()
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
--position in Earth's bodyfixed frame at time t0
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local position0 =
celestia:newpositionlonglat(math.rad(0), math.rad(0), microlightyears)
--How many radians do the clouds travel per day in Earth's bodyfixed frame?
local radiansPerDay = earth:getinfo().atmosphereCloudSpeed
local function tickHandler()
local t = celestia:gettime() - t0 --number of days since t0
local rotation = celestia:newrotation(-std.yaxis, t * radiansPerDay)
observer:setposition(bodyfixedFrame:from(rotation:transform(position0)))
observer:lookat(
bodyfixedFrame:from(std.position0),
bodyfixedFrame:from(std.yaxis))
end
local function main()
celestia:hidelabel("planets")
earth:addreferencemark({type = "body axes"})
observer:setframe(bodyfixedFrame)
--one simulation day per 15 seconds of real time
celestia:settimescale(60 * 60 * 24 / 15)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Here’s another way to keep the observer aimed at the center of the Earth,
with the bodyfixed Y axis pointing up.
Create the following orientation immediately after the local
position0.
--The orientation that would make an observer at position0 look towards the
--center of the Earth, with the Y axis pointing up.
local orientation0 =
celestia:newrotationforwardup(std.position0 - position0, std.yaxis)
Then change the call to
Observer:lookatObserver:lookat
to the following.
observer:setorientation(bodyfixedFrame:from(rotation * orientation0))
A handler called 60 times per second should be as fast as possible.
It would therefore be desirable to remove the
Observer:lookatObserver:lookat
and the
Observer:setorientationObserver:setorientation
from the handler.
But how will we keep the observer aimed at the center of the Earth,
with
Polaris
up?
The method
Observer:trackObserver:track
seems promising.
It keeps the observer
pointedtrack a celestial object
at a celestial object
by automatically executing the following code with each tick of the Celestia
simulation.
At first glance,
the code seems to keep the observer’s up vector unchanged.
But
track
actually offers no such guarantee.
For example, consider an observer whose tracked object is at
Taurus/Gemini
and whose zenith is at
Draco.
If the tracked object moves down to
Orion,
the observer’s zenith will move down to
Polaris.
So far,
this seems harmless:
his up vector has moved down the solstitial colure,
as it had to,
but it has not strayed to the left or right.
If the tracked object now moves to the right along the celestial equator,
from
Orion
to
Pisces,
the up vector will remain pointing to
Polaris.
This seems even better:
his up vector has remained completely motionless.
But his original up vector,
pointing towards
Draco,
is now pointing off towards the observer’s current upper right.
His current zenith, near
Polaris,
has wandered away from his original zenith in
Draco.
We can still use
Observer:track
in this program, but it requires care.
We will avoid the “wandering zenith” problem
by positioning and orienting the observer
before we start tracking the Earth.
Insert the following code into the
main
function immediately after the
Observer:setframe.
Then remove the
Observer:lookat
or
setorientation
in the handler.
The observer will remain in the plane of the Earth’s equator
while tracking is in effect.
The
track
method will yaw his direction of view left or right
as he circles the Earth,
but it will never pitch him up or down.
Polaris will remain at his zenith
and his up vector will never wander.
Tracking can be turned off by passing
nilnil (Lua value)
to
Observer:track.
What would happen if we turn tracking on
when the observer is
already locateddivision by zero
at the position of the tracked object?
With the
Observer:lookat
and
Observer:setorientation
out of the way, the body of the handler can be reduced to a single statement.
Does this make the program run any more smoothly?
Does it make the code harder to read?
We could remove the handler entirely if we had a frame of reference that moved with the clouds. Come back to this program after you have read about the scripted rotations in scriptedRotation.
Since the Earth’s rotation exactly matches their period, they face always one side of the Earth—the ninetieth western meridian, to be exact. Their orbit lies in the ecliptic, the plane of the Earth’s orbit around the Sun, rather than in the plane of the Earth’s equator. This results in them swinging north and south each day as seen from the Earth. When it is noon in the Middle West, Terra Station and the Randolph lie over the Gulf of Mexico; at midnight they lie over the South Pacific.
Let’s station the observer on board the
Randolph
and gaze down at the Earth.
The following
position0
is measured with respect to the Earth’s bodyfixed frame.
It remains fixed above the Galápagos Islands on the equator—at
the ninetieth western meridian, to be exact.
As the Earth rotates,
the position circles the Earth in exactly twenty-four hours
in the plane of the equator.
The plane of this orbit is rotated
23°
into the plane of the ecliptic by the call to
Rotation:transform.
The axis of this rotation must be the X axis
of the Earth’s ecliptic frame.
To cause the axis to be interpreted with respect to this frame,
the position being rotated must first be converted to the frame.
(The conversion goes from bodyfixed to universal,
and then from universal to ecliptic.)
We can confirm that the observer is now in the plane of the ecliptic
because the red line of the ecliptic passes directly behind the Earth.
--[[
Look at the Earth from the school ship Randolph,
in geosynchronous orbit in the plane of the ecliptic.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
local eclipticFrame = celestia:newframe("ecliptic", earth)
local rotation = std.radecRotation:conjugateRotation:conjugate() --Mexico at noon, not midnight
local microlightyears = 42164 / KM_PER_MICROLY --height of geosynchronous orbit
local position0 =
celestia:newpositionlonglat(math.rad(-90), math.rad(0), microlightyears)
local function tickHandler()
local position = bodyfixedFrame:from(position0)
position = eclipticFrame:to(position)
position = rotation:transform(position)
observer:setposition(eclipticFrame:from(position))
--Prevent Polaris from swaying left and right.
observer:lookat(earth:getposition(), bodyfixedFrame:from(std.yaxis))
end
local function main()
celestia:hidelabel("planets") --interferes with celestia:mmprint
celestia:select(earth)
for i, t in
ipairs({"body axes", "planetographic grid", "sun direction"}) do
earth:addreferencemark({type = t})
end
observer:setframe(bodyfixedFrame)
celestia:mmprint()
celestia:settime(celestia:utctotdb(2075, 6, 21, 4, 41)) --solstice
--One day of simulation time per 30 seconds of real time
celestia:settimescale(60 * 60 * 24 / 30)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Change
std.radecRotation:conjugate()
to plain old
std.radecRotation.
Observe that the
Randolph
is now over the Gulf of Mexico at midnight, not noon.
Keep the ecliptic horizontal by changing the second argument of
Observer:lookat
to
std.yaxis.
Does this make the display more pleasing?
Display the current latitude and longitude of Terra Station and the Randolph.
Instead of hardwiring in the radius of the geosynchronous orbit, compute it with the machinery in Impulse.
Terra Station and the Randolph reach their northernmost point at noon, and their southernmost point at midnight, only on the day of the summer solstice. But in the Heinlein novel, Matt DodsonDodson, Matt reports to the cadets in Colorado on “One July, 2075”. Was the author implying that the on-the-ground training lasts almost a full year?
john glenn [aboard Friendship 7Friendship 7 (spacecraft)]. Roger. I do have the lights in sight on the ground. Over.
gordon cooperCooper, Gordon [capcom at MucheaMuchea Tracking Station, Western AustraliaAustralia]. Roger. Is it just off to your right there?
glenn. That’s affirmative. Just to my right I can see a big pattern of lights apparently right on the coast. I can see the outline of a town and a very bright light just to the south of it. On down …
cooper. PerthPerth, Australia and RockinghamRockingham, Australia you’re seeing there.
glenn. Roger. The lights show up very well, and thank everybody for turning them on, will you?
cooper. We sure will, John.
Let’s trace the path of John Glenn’s three orbits in Friendship 7. The plane of the orbit remains fixed in space as the Earth rotates beneath him, creating the “waves out of phase” diagram that was the trademark of the mission controlsmission control of the early 1960’s.
We will create a
glennFrame
whose origin is the center of the Earth
and whose XZ plane is the plane of Glenn’s orbit.
To determine the plane, we will locate three points on it.
These points will be the center of the Earth,
the launch pad at Cape Canaveral
(on the X axis of the
glennFrame),
and the
ascending
nodeascending node (orbital element)
(the point where the orbit crosses the Earth’s equator on its way north).
We already know where the first two points are.
The following diagram shows an edge-on view of the plane of the orbit
at the instant of launch
and will help us compute the distance from point A to point C.
The sides of the triangle are segments of great circlesgreat circle on the surface of the Earth, so their lengths can be represented as degrees or radians of arc. For example, the length of the vertical side a is 28.49117° of latitude. This is equal to the number of degrees in the angle BOC, where O is the center of the Earth. We call this the angular lengthangular length (of segment of great circle) of the side. We will solve for the angular length of side c and then for side b.
We use an uppercase letter for an angle whose vertex is on the surface of the Earth, and lowercase for an angle whose vertex is at the center of the Earth. For example, angle A is 32.54° and angle a is 28.49117°.
The spherical law of sinesspherical law of sines gives us an equation we can solve for c. sin A sin a = sin B sin b = sin C sin c We need only the first and third parts of the equation. sin A sin a = sin C sin c We can solve it for sin c sin c = sin a sin C sin A and then for c itself: c = arcsinarcsine (trig function) sin a sin C sin A Since our angle C is 90°, the sin C turns into a simple 1.
Armed with the value of c, we proceed to the spherical law of cosinesspherical law of cosines: cos c = cos a cos b + sin a sin b cos C Since our angle C is 90°, the law simplifies to cos c = cos a cos b We can solve it for cos b cos b = cos c cos a and then for b itself: b = arccosarccosine (trig function) cos c cos a We now have the angular length along the equator from the ascending node to Ecuador.
The origin of the
glennFrame
will be the center of the Earth,
with the X axis pointing towards Canaveral at launch time.
To determine the Y axis,
the following program creates vectors from the origin
to the ascending node and to Canaveral.
Their cross product will be used as the Y axis,
pointing towards the orbit’s north pole in eastern Siberia.
The axes of the
glennFrame
remain stationary with respect to the Earth’s ecliptic frame.
As the Earth rotates,
Canaveral will therefore move away from the X axis.
To keep things simple, many issues are ignored. Our Earth is a sphere, our orbit is a circle, and the speed of our spacecraft is constant. In real life, the spacecraft had to pick up speed gradually. We therefore penalize the simulated spacecraft by 15.5 degrees of arc by launching it from the waters of the Gulf of Mexico. (The 15.5° is an empirical value that gets Glenn to Perth on schedule. Note that he flies over that city on only his first orbit.) We also fly without retrorockets or parachutes. The simulated spacecraft overshoots its landing zone and then comes to an abrupt halt.
--[[
Follow John Glenn's three orbits as the Earth rotates beneath him.
Glenn and the center of the Earth stay at the center of the window.
The XZ plane of the glennFrame remains horizontal.
]]
require("std")
--variables used by tickHandler:
local t0 = celestia:utctotdb(1962, 2, 20, 14, 47, 39) --launch
local t1 = celestia:utctotdb(1962, 2, 20, 19, 43, 2) --splashdown
local period = (88 + 29 / 60) / (60 * 24) --length of orbit, in days
local earth = celestia:find("Sol/Earth")
local microlightyears = 2 * earth:radius() / KM_PER_MICROLY --observer altitude
local observer = celestia:sane()
local glennFrame = nil
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
--The real Glenn had to pick up speed gradually,
--so we penalize the simulated Glenn by this amount.
local fudge = math.rad(15.5)
local function createGlennFrame()
--Vector in Earth's bodyfixed frame from center of Earth
--to Launch Complex 14 at Cape Canaveral, Florida.
local latCanaveral = math.rad(28.49117)
local longCanaveral = math.rad(-80.546983)
local toCanaveral =
celestia:newvectorlonglat(longCanaveral, latCanaveral)
--Vector in Earth's bodyfixed frame from center of Earth
--to ascending node of Glenn's orbit.
local inclination = math.rad(32.54)
local a = latCanaveral
local c = math.asin(math.sin(latCanaveral) / math.sin(inclination))
local b = math.acos(math.cos(c) / math.cos(a))
local toNode = celestia:newvectorlonglat(longCanaveral - b, 0)
--Convert vectors from Earth's bodyfixed frame to universal frame.
toCanaveral = bodyfixedFrame:from(toCanaveral)
toNode = bodyfixedFrame:from(toNode)
--[[
The origin of the glennFrame is the center of the Earth.
The XZ plane is the plane of Glenn's orbit.
The X axis points towards Cape Canaveral.
The Y axis points towards north pole of orbit, in eastern Siberia.
]]
local up = toNode ^ toCanaveral --positive Y axis of glennFrame
local forward = up ^ toCanaveral --negative Z axis of glennFrame
local rotation = celestia:newrotationforwardup(forward, up)
return celestia:newframe("ecliptic", earth, rotation)
end
local function tickHandler()
local t = celestia:gettime()
if t > t1 then
celestia:settimescale(1)
end
t = t - t0 --elapsed time since launch
--Radians of arc traveled in glennFrame since launch.
--The simulated Glenn moves at a constant speed.
local theta = 2 * math.pi * t / period - fudge
--Don't let theta grow too big for celestia:newpositionlonglat
theta = math.fmodmath.fmod(theta, 2 * math.pimath.pi);
local position = celestia:newpositionlonglat(theta, 0, microlightyears)
position = glennFrame:from(position)
observer:setposition(position)
observer:lookat(earth:getposition(), glennFrame:from(std.yaxis))
local longlat = bodyfixedFrame:to(position):getlonglat()
local dhms = std.todhmsstd.dhms(t) --days, hours, minutes, seconds
local s = string.format(
"T plus %02d:%02d:%02d\n" --T stands for takeoff time
.. "Lat %g%s\n"
.. "Long %g%s",
dhms.hours, dhms.minutes, math.floor(dhms.seconds),
math.deg(longlat.latitude), std.char.degree,
math.deg(longlat.longitude), std.char.degree)
celestia:mmprint(s)
end
local function main()
--Launch the spacecraft as soon as the "CELESTIA" logo disappears.
--The celestia:settime must come before bodyfixedFrame:from.
celestia:settime(t0 - std.logo / (60 * 60 * 24))
--The "Earth" label interferes with the "MM" of Celestia:mmprint.
celestia:hidelabel("planets")
earth:addreferencemark({type = "planetographic gridplanetographic grid"})
glennFrame = createGlennFrame()
observer:setframe(glennFrame)
local position = celestia:newpositionlonglat(-fudge, math.rad(0),
microlightyears)
observer:setposition(glennFrame:from(position))
observer:lookat(earth:getposition(), glennFrame:from(std.yaxis))
celestia:mmprint()
wait(std.logo) --until "CELESTIA" logo disappears
--one orbit per minute of real time
celestia:settimescale(period * 24 * 60)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
T plus 00:00:03
Lat 23.2427°
Long 263.445°
Accelerate from zero to orbital speed during the five minutes and 1.4 seconds of powered flight, and decelerate back to zero between retrofire and splashdown.
According to We Seven, the retrorocketsretros are fired 2990 miles from the point of splashdown. Position Friendship 7 so that a retro fire at 19:20:11 UTC would result in a splash down at 19:43:02 UTC at 21° 20′ N 60° 40′ W. Then compute where the capsule be when powered flight ends at T plus 5 minutes and 1.4 seconds.
Flash the names of the Project Mercury tracking stations as Friendship 7 passes within range of them.
Simulate the view through Glenn’s window. Let the user manually yaw, pitch, and roll, but keep track of how much hydrogen peroxide he or she uses.
Terrified Americans awoke on October 5, 1957 to find a SputnikSputnik 1 (spacecraft) sailing over their heads. “The Naval Research LaboratoryNaval Research Laboratory, United States announced early today that it had recorded four crossings of the Soviet earth satellite over the United States,” reported The New York Times. “It said that one had passed near Washington. Two crossings were farther to the west. The location of the fourth was not made available immediately.”
Stem the panic by locating the fourth crossing of the satellite. Sputnik 1 was launched at 19:28:34 UTC October 4, 1957 from Pad 1 of what we now call the Baikonur CosmodromeBaikonur Cosmodrome at 45° 55′ 13″ N 63° 20′ 32″ E, with an orbital inclination of 65.1° and a period of 96.2 minutes. Like Friendship 7, its initial heading was northeast. When you have the answer, get President EisenhowerEisenhower, Dwight D. on the phone.
Although a galaxy does not rotate the Celestia universe, it has a bodyfixed frame anyway. The origin is at the center of the galaxy, but the axes have no relation to the galaxy’s axis and plane. The bodyfixed X axis always points in the opposite direction from the universal frame X axis. The bodyfixed Y axis points in the same direction as the universal Y axis. The bodyfixed Z axis points in the opposite direction from the universal Z axis.
--Print the axes of the bodyfixed frame in universal coordinates. local galaxy = celestia:find("Milky Way") --or "M 31" for Andromeda local bodyfixedFrame = celestia:newframe("bodyfixed", galaxy) local s = "" --Convert the three bodyfixed axes to universal. for c in std.xyzstd.xyz() do
local name = c .. "axis"
local axis = bodyfixedFrame:from(std[name])
s = s .. string.format("%s = (%2g, %2g, %2g)\n",
name, axis:getxyz())
end
celestia:print(s, 60)
xaxis = (-1, 0, 0)
yaxis = ( 0, 1, 0)
zaxis = ( 0, 0, -1)
A
180°
rotation around the universal Y axis would therefore be necessary
to make all three bodyfixed axes agree with their universal counterparts.
For other examples where this rotation is necessary,
see
scriptedRotation
and
Phase:getorientationPhase:getorientation.
Let’s implement a bodyfixed frame that agrees with the galaxy’s orientation in space. The origin will be the center of the galaxy and the XZ plane will be the galactic plane. In the case of our Milky WayMilky Way, bodyfixed frame for, the X axis will point from the origin towards the Sun. The Y axis will point up out of the galactic plane, towards the north galactic polenorth galactic pole (NGP) in Coma BerenicesComa Berenices and away from the Magellanic CloudsMagellanic Clouds. (Judging from its arms, the Milky Way’s rotation is retrograde and its Y axis should therefore point down, like Venus’s. But no one wants to open that can of worms. See the Andromeda Galaxy exercise in galacticCoordinates.) The Z axis is determined by the other two axes because all Celestia frames are right-handedright-handed frame; see framesOfReference.
Do not confuse our new bodyfixed frame with the galactic coördinates in galacticCoordinates. The origin of our new frame is the center of the galaxy; the origin in galacticCoordinates was in the Solar System.
The following orientation for the Milky Way
is in the file
data/galaxies.dscgalaxies.dsc (file).
We will combine it with the above
180°
rotation to create the new bodyfixed frame
--[[
Give the Milky Way a milkyFrame frame that agrees with the shape and orientation
of the galaxy. The origin is the center of galaxy, the XZ plane is the galactic
plane. The X axis points towards the Sun, the Y axis towards north galactic
pole in Coma Berenices.
Position the observer on the positive Z axis, with the X axis pointing right and
the Y axis pointing up. The Magellanic Clouds are below the galactic plane. To
rotate the observer around the galaxy, Option-drag on Mac, right-drag on
Microsoft Windows.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local milkyWay = celestia:find("Milky Way")
local rotation = celestia:newrotation(
celestia:newvector(0.4372, -0.7548, -0.4891), --from data/galaxies.dsc
math.rad(99.6995)
) * celestia:newrotation(std.yaxis, math.rad(180))
local milkyFrame = celestia:newframe("bodyfixed", milkyWay, rotation)
local function tickHandler()
local position = observer:getposition()
position = milkyFrame:to(position)
local longlat = position:getlonglat()
local s = string.format(
"latitude: %g%s\n"
.. "longitude: %g%s\n"
.. "distance from center: %g lightyears = %g kiloparsecs",
math.deg(longlat.latitude), std.char.degree,
math.deg(longlat.longitude), std.char.degree,
longlat.distance / 1e6,
longlat.distance / (1e9 * std.lyPerPc))
celestia:mmprint(s, 1)
end
local function main()
celestia:hide("ecliptic", "grid")
celestia:show("galacticgrid")
celestia:select(milkyWay)
milkyWay:mark("white", "plus") --white plus at center of galaxy
--Sun on positive X axis.
celestia:find("Sol"):mark("yellow", "disk", 5, .9, "Sun")
--Globulars too faint to see from this distance unless we mark them.
for dso in celestia:dsos() do
if dso:type() == "globular" then
dso:mark("white", "filledsquare", 1) --single pixel
end
end
observer:setframe(milkyFrame)
local microlightyears = 5 * 1e6 * milkyWay:getinfo().radius
local position = celestia:newposition(0, 0, microlightyears)
observer:setposition(milkyFrame:from(position))
observer:lookat(milkyWay:getposition(), milkyFrame:from(std.yaxis))
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Since we are initially on the positive Z axis, our longitude is 270° East.
MM latitude: -0.00247203° longitude: 269.999° distance from center: 250028 lightyears = 76.6589 kiloparsecs
How far does Celestia’s stellar database extend across the galaxy?
Find the star in the database
that is farthest from the origin of the universal frame.
Then have the above program
mark
every star
that is more than .3 times this distance
from the origin of the universal frame.
It’s easy to see the galaxies that are above and below the plane of the Milky Way. But the body of the galaxy blocks our view of the galaxies that lie in the plane, creating the illusion of a galaxy-free band called the Zone of Avoidance.
--[[ Pull away from the Milky Way, looking back at the center of the galaxy as we leave it behind. Go to a point way out at SGL 0 SGB 0 where we have edge-on views of the Galactic Plane (the plane of the Zone of Avoidance, initially horizontal) and the supergalactic plane (colored green). When the goto has finished, rotate the observer around the Milky Way with option-drag on Mac, right-drag on Microsoft Windows. ]] require("std") --variables used by tickHandler: local observer = celestia:sane() local galacticFrame = celestia:newframe("universal", std.galacticRotationSupergalactic plane edge-on at ℓ = 137° and 317°, b = 0°. ℓ = 137.37° b = 0.00417302°std.galacticRotation) local milkyWay = celestia:find("Milky Way") local function tickHandler() --Keep it selected even if the user clicks another galaxy. celestia:select(milkyWay) local longlat = galacticFrame:to(observer:getposition()):getlonglat() local s = string.format( "Supergalactic plane edge-on " .. "at %s = 137%s and 317%s, b = 0%s.\n" .. "%s = %g%s\n" .. "b = %g%s", std.char.l, std.char.degree, std.char.degree, std.char.degree, std.char.l, math.deg(longlat.longitude), std.char.degree, math.deg(longlat.latitude), std.char.degree) celestia:print(s) end local function main() celestia:hide("ecliptic", "grid") celestia:show("galacticgrid") celestia:select(milkyWay) local rotation = celestia:newrotation( celestia:newvector(0.4372, -0.7548, -0.4891), --galaxies.dsc math.rad(99.6995) ) * celestia:newrotation(std.yaxis, math.rad(180)) local milkyFrame = celestia:newframe("bodyfixed", milkyWay, rotation) observer:setposition(std.position) observer:lookat(milkyWay:getposition(), milkyFrame:from(std.yaxis)) wait() local supergalacticFrame = celestia:newframe("universal", std.supergalacticRotation) --Galaxies belonging to clusters belonging to superclusters along the --supergalactic plane. local clusters = { {"M 87", "Virgo"}, {"NGC 1275", "Persus"}, {"NGC 383", "Pisces"}, {"NGC 3309", "Hydra"}, {"NGC 4696", "Centaurus"}, {"IC 4765", "Pavo"} } for i, value in ipairs(clusters) do local galaxy = celestia:find(value[1]) galaxy:mark("yellow", "disk", 5, .9, value[2]) end for dso in celestia:dsos() do if dso:type() == "galaxy" then local position = dso:getposition() position = supergalacticFrame:to(position) local color = "white" if math.abs(position:gety()) < 5e12 then color = "green" --along supergalactic plane end --Has no effect on galaxies that are already marked. dso:mark(color, "filledsquare", 1) end end wait() --The vector toCassiopeia lies along the intersection of the galactic --and supergalactic planes, pointing towards SGL 0 SGB 0 in Cassiopeia. local toCassiopeia = milkyFrame:from(std.yaxis) ^ supergalacticFrame:from(std.yaxis) local microlightyears = 2.5e4 * 1e6 * milkyWay:getinfo().radius local to = (microlightyears * toCassiopeia:normalize()):toposition() observer:trackObserver:track(milkyWay) --while goto is in progress local duration = 20 observer:goto({duration = duration, to = to}) wait(duration) observer:track(nil) --turn off tracking celestia:registereventhandler("tick", tickHandler) wait() end main()
Let’s assume the observer is in New York City (not exactly a premier site for astronomy). What would be the simplest frame of reference for measuring the altitudealtitude (vs. azimuth) and azimuth of a celestial body from his point of view? Ideally, the origin would be at New York. The XZ plane would be the plane of the horizon, with the X axis pointing east and the Z pointing south. The Y axis would point straight up.
The standard library gives us a frame that is almost as good.
The following
altazFrame
has its origin at the center of the Earth,
not at New York,
but its axes are parallel to those above.
The frame is created with the rotation returned by
Celestia:newrotationaltazCelestia:newrotationaltaz.
There is one minor complication.
Azimuth is measured to the right from due north,
while longitude would be measured to the left from due east.
(Viewed from the center of the Earth,
east longitude is measured to the
left
of the Prime Meridian.)
That’s why we have to call
Vector:getaltazVector:getaltaz
instead of
Vector:getlonglatVector:getlonglat.
Chaucer’s Astrolabe is the Anglosphere’s answer to the ancient Greek Antikythera mechanismAntikythera mechanism. In the instructions, the astrolabe dangled vertically from a ring on the thumb of the user’s upraised right hand. Nowadays we would use Celestia to know the altitude of the Sun or of other celestial bodies. Let’s put the observer in New York City at 17:00 UTC (noon in Eastern Standard Time) on January 1 of the current year.
--[[
Print the altitude and azimuth of the Sun as seen from New York City.
The origin of the altazFrame is the center of the Earth.
The XZ plane of the frame is parallel to the plane of the horizon at New York.
The X axis is parallel to the vector pointing east from New York.
The Z axis is parallel to the vector pointing south from New York.
The Y axis points from the center of the Earth straight up through New York.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("grid")
celestia:show("horizontalgrid")
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
--New York City is 5 time zones behind UTC.
celestia:settime(celestia:utctotdb(year, 1, 1, 12 + 5))
local sol = celestia:find("Sol")
celestia:select(sol)
local earth = celestia:find("Sol/Earth")
--New York City
local latitude = math.rad( 40 + (39 + 51 / 60) / 60 ) --north positive
local longitude = math.rad(-(73 + (56 + 19 / 60) / 60)) --west negative
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
local microlightyears = (earth:radius() + .002) / KM_PER_MICROLY
local nycPosition = bodyfixedFrame:from(celestia:newpositionlonglat(
longitude, latitude, microlightyears))
observer:setposition(nycPosition)
--Center of earth at observer's nadir.
local solPosition = sol:getposition()
observer:lookat(solPosition, nycPosition - earth:getposition())
local rotation = celestia:newrotationaltaz(longitude, latitude)
local altazFrame = celestia:newframe("bodyfixed", earth, rotation)
--vector in universal coordinates
local toSol = solPosition - nycPosition
--vector in New York City altazimuth coordinates
toSol = altazFrame:to(toSol)
local altaz = toSol:getaltaz()
local alt = std.tolat(altaz.altitude)
assert(alt.signum > 0) --Sun is above the horizon.
local az = std.toaz(altaz.azimuth)
local s = string.format(
"altitude %s%s %s%s %.15g%s\n"
.. "azimuth %d%s %d%s %.15g%s",
alt.degrees, std.char.degree,
alt.minutes, std.char.minute,
alt.seconds, std.char.second,
az.degrees, std.char.degree,
az.minutes, std.char.minute,
az.seconds, std.char.second)
celestia:print(s, 60)
wait()
end
main()
The winter Sun is low in New York’s southern sky. At noon, the Sun’s azimuth should be approximately 180° (due south). A little bit is added to the azimuth because New York is east of 75° West, the meridian of Eastern Standard Time. And a little bit is subtracted because of the equation of timeequation of time in January; see Analemma.
altitude 26° 23′ 22.2631053548039″ azimuth 180° 5′ 36.1690824181096″In the days before air conditioning, steamship passengers going outbound from Britain to India tried to avoid the sun by getting staterooms on the port (left) side of the ship. Passengers going home preferred the starboard (right) side. The word “posh”posh was originally an acronym. What did it stand for?
Read the program in celestialDome that displays the altitude and azimuth of the direction in which the observer is looking.
The Korean War ended on July 27, 1953 at 10:00 a.m. Korean time (9 hours ahead of UTC). New York City has a memorial sculpture in Battery Park, visible in Google Maps in a circle in the trees at latitude 40.704017° N, longitude 74.017095° W. Every year on July 27 at 10:00 a.m. New York time (5 hours behind UTC), the sun shines through the silhouette of the soldier’s head onto a commemorative plaque. Find the altitude and azimuth of the Sun at that place and time in the current year.
Locate the photograph and determine when it was taken. The Washington Monument is at latitude 38° 53′ 22.08377″ North, longitude 77° 2′ 6.86378″ West.
I’m in New York City and I’d like to face Mecca.
We’ll settle for Washington D.C. and Cairo,
which are present in the file
data/world-capitals.sscworld-capitals.ssc (file).
In what direction (azimuth) should I face?
And if I wanted to tunnel straight to Cairo,
at what pitch (altitude) should I dig?
--[[
Position the observer above Washington, with the Earth centered in the window
and Cairo towards the top. We can then read Cairo's approximate azimuth from
the horizontal (altazimuth) grid in the sky. Print the exact azimuth.
The origin of the altazFrame is the center of the Earth.
The XZ plane of the frame is parallel to the plane of the horizon at Washington.
The X axis is parallel to the vector pointing east from Washington.
The Z axis is parallel to the vector pointing south from Washington.
The Y axis points from the center of the Earth straight up through Washington.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("grid")
celestia:show("horizontalgrid")
celestia:showlabel("locations") --cities, etc.
local earth = celestia:find("Sol/Earth")
earth:addreferencemark({type = "planetographic grid"})
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
local washington = celestia:find("Sol/Earth/Washington D.C.")
local washingtonPosition = washington:getposition()
washington:mark("white", "plus", 10)
local cairo = celestia:find("Sol/Earth/Cairo")
local cairoPosition = cairo:getposition()
cairo:mark("white", "plus", 10)
--Get Washington's latitude and longitude.
local longlat = bodyfixedFrame:to(washingtonPosition):getlonglat()
--XZ plane of altazFrame is parallel to surface of Earth at Washington.
local rotation =
celestia:newrotationaltaz(longlat.longitude, longlat.latitude)
local altazFrame = celestia:newframe("bodyfixed", earth, rotation)
observer:setframe(altazFrame)
--Observer's position in altazFrame: directly above Washington.
local position = celestia:newposition(
0,
5 * earth:radius() / KM_PER_MICROLY,
0)
observer:setposition(altazFrame:from(position))
--Vector in universal frame, pointing from Washington to Cairo.
local toCairo = cairoPosition - washingtonPosition
--Cairo towards top of window, top of plus sign just barely visible.
observer:lookat(earth:getposition(), toCairo)
local altaz = altazFrame:to(toCairo):getaltaz()
local s = string.format(
"azimuth from Washington to Cairo: %g%s\n"
.. "altitude (to tunnel straight to Cairo): %g%s",
math.deg(altaz.azimuth), std.char.degree,
math.deg(altaz.altitude), std.char.degree)
local duration = 60
celestia:print(s, duration)
wait(duration)
end
main()
The top of Cairo’s write plus is just barely visible.
azimuth from Washington to Cairo: 55.7187° altitude (to tunnel straight to Cairo): -42.0451°
If Cairo were the antipode of Washington,
the call to
Observer:lookat
would
divide by zerodivision by zero.
What would be a sensible thing to do instead?
Now print the azimuth and altitude from New York City to Mecca. Get the latitude and longitude of these cities from Wikipedia.
--Positions in Earth's bodyfixedFrame. local meccaPosition = celestia:newpositionlonglat( math.rad( 39 + 49/60), --East longitude is positive. math.rad( 21 + 25/60)) --North latitude is positive. local nyPosition = celestia:newpositionlonglat( math.rad(-(73 + (56 + 19 / 60) / 60)), --west longitude negative math.rad( 40 + (39 + 51 / 60) / 60 )) --north latitude positive --Positions in universal frame. nyPosition = bodyfixedFrame:from(nyPosition) meccaPosition = bodyfixedFrame:from(meccaPosition) azimuth from New York to Mecca: 58.5393° altitude (to tunnel straight to Mecca): -46.3334°Is the New York City mosqueIslamic Cultural Center of New York aligned correctly? View it in Google Maps at latitude 40.785446° North longitude 73.948554° West (on the east side of Third Avenue between 96th and 97th Streets). To get the latitude and longitude of each corner of the building, right-click and select “What’s here?”. The west corner (on Third Avenue) is at approximately 40.785498° North 73.948777° West. The north corner (on East 97th Street) is at 40.785629° North 73.948507° West. Let’s print the azimuth that takes us from the west corner to the north corner.
--Positions in bodyfixedFrame. Assume Earth is a sphere. local northCorner = celestia:newpositionlonglat( math.rad(-73.948507), --West longitude is negative. math.rad(40.785629), --North latitude is positive. earth:radius() / KM_PER_MICROLY) local westCorner = celestia:newpositionlonglat( math.rad(-73.948777), math.rad(40.785498), earth:radius() / KM_PER_MICROLY) --Vector in universal frame showing which way the mosque is pointing. local v = bodyfixedFrame:from(northCorner) - bodyfixedFrame:from(westCorner) --Get the azimuth of the vector in the mosque's altazFrame. local s = string.format("The mosque points towards azimuth %g%s.", math.deg(altazFrame:to(v):getaltaz().azimuth), std.char.degree) The mosque points towards azimuth 57.3484°.Viewed through a transparent Earth from New York, would California really be the length of a thumb held at arm’s length? How far underground (i.e., at what altitude) would it appear to be? Ignore any diffraction from the crystalline Earth.
Prepare a report for the Royal Air Force.
Invent a rotated frame whose origin is the center of the Earth and whose Y axis points towards Mecca—or towards London. Or towards the subsolar point on the Earth, or towards the center of the leading hemisphere of the Earth. The latter would have been a big help for MichelsonMichelson, Albert and MorleyMorley, Edward when they set up their experimentMichelson-Morley experiment; you will need the “chase frame” in chaseFrame;
Viewed from the surface of Mercury, the hesitating terminator (hesitantTerminator) translates into a bobbing sunrise.
--[[
Watch the bobbing sunrise from the surface of Mercury,
visible only from the meridians of 90 E and 90 W.
]]
require("std")
local function main()
local observer = celestia:sane()
--With the narrow field of view, galaxies are too bright.
celestia:hide("grid", "ecliptic", "galaxies")
celestia:setambientCelestia:setambient(.3) --so we can see Mercury's surface even at night
--With the narrow field of view, too many things are labeled.
local flags = celestia:getlabelflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setlabelflags(flags)
local mercury = celestia:find("Sol/Mercury")
local bodyfixedFrame = celestia:newframe("bodyfixed", mercury)
observer:setframe(bodyfixedFrame)
--a point on the great circle of bobbing sunrise
local lat = math.rad(0)
local long = math.rad(90) --East is positive.
--1 meter above the surface of Mercury to avoid jitterjitter (of planetary surface)
local microlightyears = (mercury:radius() + .001) / KM_PER_MICROLY
local position = celestia:newpositionlonglat(long, lat, microlightyears)
observer:setposition(bodyfixedFrame:from(position))
local rotation = celestia:newrotationaltaz(long, lat)
local altazFrame = celestia:newframe("bodyfixed", mercury, rotation)
--Face the eastern horizon. Azimuth of east is 90 degrees.
local forward = celestia:newvectoraltaz(math.rad(0), math.rad(90))
local up = celestia:newvectoraltaz(math.rad(90), math.rad(0))
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(altazFrame:from(orientation))
celestia:settime(celestia:utctotdb(2013, 5, 3)) --just before sunrise
--Make the Sun span one-third of the vertical field of view.
local sol = celestia:find("Sol")
local angularRadius = math.asinmath.asin(sol:radius()
/ observer:getposition():distanceto(sol:getposition()))
local angularDiameter = 2 * angularRadius
observer:setverticalfov(3 * angularDiameter)
--One Earth day of simulation time per second of real time
celestia:settimescale(60 * 60 * 24)
wait()
end
main()
Simplify
up
to one of the following.
Watch the bobbing sunset on
Mercury.
Face west by changing the azimuth to
math.rad(270).
Set the time to half of a Mercurian solar day later than the above time.
Watch the bobbing Earthrise and Earthset from the surface of Mare MarginisMare Marginis (lunar sea) (hesitantTerminator) on the Moon. Face west (azimuth 270°), and pitch the camera up to altitude 5° to see more of the sky. Start with a vertical field of view of 35 times the Earth’s angular diameter, and adjust to taste.
Watch the bobbing Saturnrise and Saturnset from TitanTitan (moon of Saturn). Position the observer 1 meter above the surface of Titan at latitude 0° North, longitude 90° East. Face west (azimuth 270°). Since Saturn doesn’t bob up and down as much as the Earth in the previous exercise, you can reduce the vertical field of view to 5 times Saturn’s angular diameter.
You’ll have to
hide
Titan’s clouds in order to see Saturn.
But let the
"atmospheres"atmospheres (renderflag)
remain,
as a tribute to
Chesley
BonestellBonestell, Chesley’s
painting
Saturn as Seen from TitanSaturn as Seen from Titan (Bonestell painting).
Can we tilt the rings by positioning the observer at a different latitude?
Is there any way we could simulate this in Celestia?
וְ֗הוּא
כְּ֭חָתָן
יֹצֵ֣א
מֵחֻפָּת֑וֹ
יָשִׂ֥ישׂ
כְּ֜גִבּ֗וֹר
לָר֥וּץ
אֹֽרַח׃
The lines on a sundial have to be plotted at slightly different angles for every date and every location. Let’s draw a customized dial, accurate for today’s date in New York City.
The easiest type of dial to fabricate is the horizontal sundial, consisting of a horizontal faceface of sundial and a vertical gnomongnomon of sundial. The face is the plate on which the lines are drawn. The gnomon is a right triangle whose legs are horizontal and vertical and whose hypotenuse, called the stylestyle (edge) of sundial, is parallel to the axis of the Earth. In the northern hemisphere, the style should point towards Polaris. Thus the angle between the style and the face is equal to the latitude where the sundial is installed. The style casts the shadow that tells the time.
To make the face, print the window displayed by the following program and paste it onto a piece of cardboard. To make the gnomon, cut a right triangle one of whose base angles is your latitude. Use a protractor to get the correct angle.
The plane that contains the style and the Sun at a given hour
is called the
Sun’s plane.
The line that we want to draw is the shadow cast by the style.
It is the intersection of the Sun’s plane with the face.
The
renderoverlay
hook draws the shadows at intervals of one hour.
The
self.position
is the point where the style meets the face.
This position,
and the vectors
toSol,
toPolaris,
and
toZenith
are in the coördinates of New York’s
altazFrame.
The vectors point away from the position in three different directions.
The vector
toSol
points towards the Sun.
The vector
toPolaris
points along the style towards Polaris.
Their
cross product
is perpendicular to the Sun’s plane.
The vector
toZenith
points straight up.
The cross product
local alongShadow = (toSol ^ toPolaris) ^ toZenith
lies in the Sun’s plane
because it is perpendicular to
toSol ^ toPolaris.
It also lies in the face because it is perpendicular to
toZenith.
The parentheses are necessary
to counteract the right-to-left
associativityassociativity, right-to-left of ^ operator
of the
^
operator.
To draw
alongShadow
at the correct angle in the plane of the face,
we note that this plane is parallel to the XZ plane of the
altazFrame
frame.
The longitude of
alongShadow
in the XZ plane
is the angle of the vector,
measured counterclockwise from due east.
See
luaHookFunctions
for Lua hooks and the
“self.”
construction,
opengl
for OpenGL graphics and text,
and
crossProduct
for cross products.
--[[
This file is luahook.celx.
Draw the hour lines on the face of a sundial as straight lines radiating from an
origin halfway between the center of the window and the center of the bottom
edge. Label each line with its hour of the day in Standard Time: a.m. on the
left, noon in the center, p.m. on the right.
For Daylight Savings Time, add 1 to the zone. For example, New York's EDT would
be zone = -4. The lines will then be labeled in Daylight Savings Time, with
1 p.m. in the center.
]]
celestia:setluahook {
sol = nil,
earth = nil,
font = nil,
bodyfixedFrame = nil,
altazFrame = nil,
position = nil,
--New York City
latitude = math.rad( 40 + (39 + 51 / 60) / 60 ), --north latitude +
longitude = math.rad(-(73 + (56 + 19 / 60) / 60)), --west longitude -
zone = -5, --EST is 5 hours behind UTC
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
--Celestia:sane would set the renderflags.
self.sol = celestia:find("Sol")
self.earth = celestia:find("Sol/Earth")
self.font = celestia:gettitlefontCelestia:gettitlefont()
self.bodyfixedFrame =
celestia:newframe("bodyfixed", self.earth)
local rotation = celestia:newrotationaltaz(
self.longitude,
self.latitude)
self.altazFrame = celestia:newframe("bodyfixed",
self.earth, rotation)
--position of New York City in the altazFrame
self.position = celestia:newposition(
0, self.earth:radius() / KM_PER_MICROLY, 0)
end
local lines = {} --table of angles counterclockwise from east
local t0 = celestia:gettime()
local utc = celestia:tdbtoutc(t0)
for hour = 0, 24 - 1 do
local t = celestia:utctotdb(utc.year, utc.month,
utc.day, hour - self.zone)
celestia:settime(t)
local toSol = self.altazFrame:to(self.sol:getposition())
- self.position
--if Sun is above horizon at this hour
if toSol:getaltaz().altitude > 0 then
local toPolaris = self.altazFrame:to(
self.bodyfixedFrame:from(std.yaxis))
local toZenith = std.yaxis
local alongShadow =
(toSol ^ toPolaris) ^ toZenith
lines[hour] = alongShadow:getlonglat().longitude
end
end
celestia:settime(t0)
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
--Origin below center of window.
local width, height = celestia:getscreendimension()
glu.Ortho2D(
0, --left
width, --right
0, --bottom
height) --top
local min = math.minmath.min(width, height)
local max = math.maxmath.max(width, height)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING)
gl.Disable(gl.TEXTURE_2D) --disabled for graphics
if celestia:getrenderflags().smoothlines then
gl.Enable(gl.LINE_SMOOTH) --antialiasing
gl.LineWidth(1.5)
end
gl.Color(1, 1, 1, 1) --rgba
--Lines will radiate from a point that is halfway across the
--window, and one quarter of the way up from the bottom.
local xTranslate = width / 2
local yTranslate = height / 4
gl.Translate(xTranslate, yTranslate)
gl.Begin(gl.LINESgl.LINES)
for hour, theta in pairs(lines) do
local x = max * math.cos(theta)
local y = max * math.sin(theta)
gl.Vertex(0, 0)
gl.Vertex(x, y)
end
gl.End()
gl.Enable(gl.TEXTURE_2D) --enabled for text
self.font:bind()
--Label along each line, centered at a point slightly more than
--halfway out from the point from which the lines radiate.
for hour, theta in pairs(lines) do
local s = nil
if hour == 0 then
s = "midnight"
elseif hour < 12 then
s = hour .. " a.m." --ante meridiem
elseif hour == 12 then
s = "noon"
else
s = hour-12 .. " p.m." --post meridiem
end
local x = .6 * min * math.cos(theta)
- self.font:getwidthFont:getwidth(s) / 2
+ xTranslate
local y = .6 * min * math.sin(theta)
- self.font:getheightFont:getheight() / 2
+ yTranslate
gl.PushMatrix()
gl.LoadIdentity()
gl.Translate(
gl.TexelRoundgl.TexelRound(x), gl.TexelRound(y))
self.font:render(s)
gl.PopMatrix()
end
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
end
}
--[[
Provide a black background for the face of the sundial.
The Lua hook will draw the white lines on top of it.
]]
require("std")
local function main()
--Celestia:sane sets the observer's position, so don't call it.
--The observer's position will be set in the Lua hook.
local flags = celestia:getrenderflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setrenderflags(flags)
flags = celestia:getlabelflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setlabelflags(flags)
wait()
end
main()
The window would be easier to print
if the sundial was drawn with black lines on a white background.
Create the white background with the
gl.QUADSgl.QUADS
argument in
opengl.
Draw the lines for the half hours and quarter hours in a subdued color.
Draw a red line pointing towards geographical north.
It will be a vertical line dividing the face in half,
showing where to attach the gnomon.
Draw another line pointing towards
magnetic
northmagnetic north
to help the user position the sundial.
Get the
magnetic
declinationmagnetic declination
for your location from the
NOAA website.
Print the date, latitude, and longitude after the last
for
loop.
You could also print the value of the
equation
of timeequation of time
(Analemma)
for the current date.
Better yet, split the text onto four separate lines.
How many hourly lines would a summer sundial have at latitude 90° North? What would have to be changed to make a sundial for Earth’s southern hemisphere?
Pick a night with a full moon and make a moondialmoondial. Pick a night with a new moon when Jupiter is at oppositionopposition (180° away from the Sun) and make a Jupiter dial.
Make a sundial for a location on another planet. Read about the sundials aboard the SpiritSpirit (Mars rover), OpportunityOpportunity (Mars rover), and CuriosityCuriosity (Mars rover) rovers on MarsMars, sundials on.
Discover how to make a spacecraft modelsmodel (OpenGL) such as Celestia’s Cassini, Hubble, or the ISS (International Space Station). Then create a model of a sundial and attach it to the Earth at your location, making it big enough to see from space. You’ll have to give the sundial a scripted orbit (scriptedOrbit) and a scripted rotation (scriptedRotation).
Let’s consider an observer on the surface of the Earth.
For simplicity,
we will assume that he is not at a pole.
The imaginary line through his zenith
dividing his sky into east and west halves is called the
meridianmeridian.
An observer in the northern hemisphere,
looking south,
would see the universe moving from left to right across his meridian
as the hours go by.
To see the meridian line itself, show the
"horizontalgrid"horizontalgrid (renderflag)
with
Celestia:show
and look for the great circle of azimuth
0°
and
180°.
The sidereal time of the observer is the amount of time since the vernal equinoxvernal equinox and sidereal time in Pisces last crossed his meridian. But sidereal time is not intended as a measure of time. It measures the angle through which the universe has apparently rotated from the conventional starting position with the equinox on the meridian. Sidereal time describes the orientation of the universe as seen by an observer at a given longitude and at a given time. For example, an observer at a longitude and time at which his sidereal time is 0h (zero hours) would see Pisces on his meridian. An observer at a longitude whose sidereal time is 6h would see Taurus/Gemini on his meridian.
The following program prints current sidereal time
of an observer in New York City at the current time.
The vector
toEquator
points towards the point on the celestial equator
that is currently on the observer’s meridian.
The longitude of the vector is the sidereal time.
Although the sidereal time is an angle,
it is conventional to display it as 0 to 24 hours rather than 0 to 360 degrees.
--[[
Print the observer's sidereal time, updated continuously.
Aim him at the point where the celestial equator and his meridian intersect,
with Polaris towards the top of the window.
]]
require("std")
--variables used by tickHandler:
local earth = celestia:find("Sol/Earth")
local equatorialFrame = celestia:newframe("equatorial", earth)
local direction = {[1] = "E", [0] = "", [-1] = "W"}
--New York City
local latitude = math.rad( 40 + (39 + 51 / 60) / 60 ) --north is positive
local longitude = math.rad(-(73 + (56 + 19 / 60) / 60)) --west is negative
local rotation = celestia:newrotationaltaz(longitude, latitude)
local altazFrame = celestia:newframe("bodyfixed", earth, rotation)
local function tickHandler()
--vector in universal frame
local toZenith = altazFrame:from(std.yaxis)
--vector in equatorialFrame
toZenith = equatorialFrame:to(toZenith)
local ra = std.tora(toZenith:getlonglat().longitude)
local long = std.tolong(longitude) --break it into degrees, minutes, sec
local utc = celestia:tdbtoutc(celestia:gettime())
local s = string.format(
"Sidereal time %dh %dm %.15gs\n"
.. "at Longitude %d%s %d%s %.15g%s %s\n"
.. "UTC %02d:%02d:%.15g %s %d %d",
ra.hours, ra.minutes, ra.seconds,
long.degrees, std.char.degree,
long.minutes, std.char.minute,
long.seconds, std.char.second,
direction[long.signum],
utc.hour, utc.minute, utc.seconds,
std.monthName[utc.month], utc.day, utc.year)
celestia:mmprint(s)
end
local function main()
local observer = celestia:sane()
celestia:show("horizontalgrid")
observer:setframe(altazFrame)
--Position the observer in New York City.
local microlightyears = (earth:radius() + .001) / KM_PER_MICROLY
local position = celestia:newposition(0, microlightyears, 0)
observer:setposition(altazFrame:from(position))
--three vectors in universal frame
local toPolaris = equatorialFrame:from(std.yaxis)
local toZenith = altazFrame:from(std.yaxis)
local toEquator = toPolaris:erect(toZenith)
--Aim him at the point on the celestial equator that's on the meridian,
--with his zenith towards top of window.
observer:lookat(observer:getposition() + toEquator, toZenith)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
MM
Sidereal time 18h 28m 13.3153619297087s
at Longitude 73° 56′ 19.0000000000134″ W
UTC 13:21:31.0003066062927 February 20 2013
Is there any way the above program could divide by zerodivision by zero?
Let’s say we wanted to see
Taurus/Gemini
on our meridian.
When is the next time that it will be sidereal time
6h
at our longitude?
Come back to this problem after you have the
std.zero
function in
findZero.
We have been programming as if the Earth were a sphere.
And it
is
a sphere in the Celestia universe,
because the Earth’s
Oblateness
in
data/solarsys.ssc
is commented out.
But in the real universe the Earth bulges at the equator.
It is closer to an
oblate
spheroidoblate spheroid (shape of Earth),
whose cross section is an ellipse.
The semi-major and semi-minor axes in microlightyears of the ellipse
are the following
a
and
b.
For our earlier brush with
a
and
b, see
kilometer.
The geodetic longitude of a point on the surface of a spheroid is defined to be the same as the plain old geocentric longitude. The geodetic latitude of the point is defined to be d degrees North if the north celestial pole of the ellipsoid is at altitude d degrees above the horizon as seen from that point. If the ellipsoid is not a sphere, the line from the center of the ellipsoid to the point on the surface will not necessarily be perpendicular to the plane of the horizon at that point. Conversely, the line that is perpendicular to the horizon will not necessarily go through the center of the ellipsoid.
When observing a satellite in low Earth orbit, the observer should be positioned on the spheroid, not the sphere. The following program positions him on the spheroid at the geodetic latitude and longitude of New York City. How can we compute the x, y, z coördinates of this New York in the Earth’s bodyfixed frame? And how can we compute the coördinates of a point directly above New York, i.e., along a vector perpendicular to New York’s horizon?
The P1 in the above diagram is New York. The line QH is tangent to the ellipse at New York and is the plane of New York’s horizon. The angle ∠P2P1H is New York’s geodetic latitude. Let θ be the size of this angle. ∠QP1R is also θ, and ∠P1QR is the complementary angle 90° − θ.
A circle is simpler to work with than an ellipse. We can turn the ellipse into a circle of radius a by stretching the picture vertically by a factor of a/b. The length of the line P2R is therefore a/b times the length of P1R, and the tangent of ∠P2QR is a/b times the tangent of angle ∠P1QR. Therefore tan ∠P2QR = a b tan (90° − θ) and ∠P2QR = arctan ( a b tan (90° − θ))
Let
φ
be the size of this angle.
∠QP2R
is the complementary angle
90° − φ,
and
∠RP2O
is
φ.
The length of line
OP2 is a
and the length of line
OR is
a sin φ
We use this length as the value of
r
in the following program.
The
z
coördinate is negated
because the Z axis points “down” in the XZ plane.
Uncomment the Earth’s
Oblateness 0.0034
in
data/solarsys.ssc
and restart Celestia.
--[[
Position the observer above New York City on an oblate spheroid Earth, along a
vector that goes straight up from New York, perpendicular to New York's horizon.
]]
require("std")
local function main()
local observer = celestia:sane()
--New York City
local latitude = math.rad( 40 + (39 + 51 / 60) / 60 ) --north positive
local longitude = math.rad(-(73 + (56 + 19 / 60) / 60)) --west negative
local earth = celestia:find("Sol/Earth")
local info = earth:getinfo()
celestia:select(earth)
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
--Uncomment Earth's Oblateness 0.0034 in solarsys.ssc; a.k.a. flattening
local a = earth:radius() / KM_PER_MICROLY --semi-major axis, in microly
local b = a * (1 - info.oblateness) --semi-minor axis
local r = nil
if latitude == 0 then --the following math.tan would be infinite
r = a
else
local complement = math.pi / 2 - math.abs(latitude)
r = a * math.sin(math.atan(math.tan(complement) * a / b))
end
local x = r * math.cos(longitude)
local z = -r * math.sin(longitude)
local y = math.sqrt(a^2 - r^2) * b / a --formula of ellipse
if latitude < 0 then
y = -y
end
local position = celestia:newposition(x, y, z) --of New York
local s = string.format("New York is %.15g km from center of Earth.",
position:tovector():length() * KM_PER_MICROLY)
local rotation = celestia:newrotationaltaz(longitude, latitude)
local altazFrame = celestia:newframe("bodyfixed", earth, rotation)
--We will go straight up from the above position,
--along a vector perpendicular to New York's horizon.
local microlightyears = info.atmosphereHeight / KM_PER_MICROLY
local vector = celestia:newvector(0, microlightyears, 0)
position = bodyfixedFrame:from(position) + altazFrame:from(vector)
observer:setposition(position)
--Face north (azimuth 0 degrees) along the horizon.
local forward = celestia:newvectoraltaz(math.rad(0), math.rad(0))
local up = celestia:newvectoraltaz(math.rad(90), math.rad(0))
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(altazFrame:from(orientation))
celestia:print(s, 60)
wait()
end
main()
New York is 6368.97702472528 km from center of Earth.
We expect that the observer’s displayed distance from the Earth
will be 60 kilometers,
which is the
Height
of the Earth’s atmosphere in
data/solarsys.ssc.
But the displayed distance always ignores the
Oblateness
in the
.ssc
file.
SaturnSaturn, oblateness of is the most oblate planet in the Solar System. Can you land on its surface and look up at the rings? Or does Celestia believe you are inside an object if your distance from its center is less than the semi-major axis?
Each celestial object that is a satellite has its own chase frame of reference. The satellite is called the reference object of the frame, and the object around which it revolves is called the primary. The origin of the chase frame is the center of the reference object. The XY plane is the plane of the reference object’s orbit around the primary. Note that this frame’s fundamental planefundamental plane (of frame) is the XY, not the XZ.
The negative X axis points in the direction of the reference object’s motion with respect to its primary; the positive X axis points towards where the reference object came from. The Y axis points approximately towards the primary. More precisely, the Y axis is erected (erect) so that it lies in the plane of the object’s orbit and is perpendicular to the X axis. The Z axis is determined by the other two axes because all Celestia frames are right-handedright-handed frame; see framesOfReference. For the Earth, the Z axis points towards the south pole of the ecliptic in Dorado.
Please do not make a chase frame for an object that is not a satellite: Celestia wouldn’t know where to put the Y axis and would divide by zerodivision by zero. Do not make a chase frame for a satellite that is motionless with respect to its primary: Celestia wouldn’t know where to put the X axis and would divide by zero. Do not make a chase frame for a satellite that is moving directly towards or away from its primary: the X and Y axes would be colinear, a nightmare in any universe.
A warning about an inconsistency in the outer Solar System.
PlutoPluto, direction of chase frame Y axis of
revolves around the Pluto-Charon barycenter,
and the velocity vector displayed by
Object:addreferencemark
is tangent this orbit.
But Pluto’s chase frame Y axis points towards the Sun,
not towards the barycenter.
We will see in lockFrame that a chase frame is similar to a “lock” frame whose target object is the reference object’s primary. In both cases, the XY plane is the plane of the reference object’s orbit around its primary. In the chase frame, the negative X axis points in the direction of the reference’s orbit around its primary. In the lock frame, the X axis points towards the center of the reference’s primary. In both cases, the Y axis is erected to be perpendicular to the X axis.
Let’s verify that the negative X axis of the Earth’s chase frame points in the direction in which the Earth is revolving around the Sun. We’ll get that direction by comparing the Earth’s position at two successive ticks.
--[[
Chase the Earth around the Sun, keeping the Earth in front of us at the center
of the window. Look in the direction in which the Earth is revolving around the
Sun. The hemisphere of the Earth that we see is therefore the trailing
hemisphere.
]]
require("std")
--variables used by tickHandler:
local sol = celestia:find("Sol")
local earth = celestia:find("Earth")
local chaseFrame = celestia:newframe("chase", earth)
local eclipticFrame = celestia:newframe("ecliptic", sol)
local radecFrame = celestia:newframe("universal", std.radecRotation)
local oldPosition = nil --Earth's position at previous tick
--v is in universal coordinates.
--Print the right ascension and declination of the direction in which it points.
local function vectorFormat(v)
assert(type(v) == "userdata" and tostring(v) == "[Vector]")
local longlat = radecFrame:to(v):getlonglat()
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
return string.format("RA %dh %dm %.2fs Dec %s%d%s %d%s %.2f%s",
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum),
dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second)
end
--[[
Display the direction in which the chaseFrame -X axis points,
and the direction in which the Earth is moving with respect to the Sun.
They should be the same direction.
]]
local function tickHandler()
local position = eclipticFrame:from(earth:getposition())
if oldPosition ~= nil and
(oldPosition:getx() ~= position:getx()
or oldPosition:gety() ~= position:gety()
or oldPosition:getz() ~= position:getz()) then
local v = chaseFrame:from(-std.xaxis)
local w = position - oldPosition
local s = string.format(
"Look in the direction towards which Earth is moving:\n"
.. "%s (-X axis of chase frame)\n"
.. "%s (direct measurement)",
vectorFormat(v), vectorFormat(w))
celestia:print(s, 1)
end
oldPosition = position
end
local function main()
local observer = celestia:sane()
observer:setframe(chaseFrame)
--Position the observer on chaseFrame X axis, looking towards origin.
local microlightyears = 50 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(chaseFrame:from(position))
observer:lookat(
chaseFrame:from(std.position0), --Earth in front of us,
--Sun to our left,
chaseFrame:from(-std.zaxis)) --Draco overhead
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Observe that the printout agrees with the position of the Earth against the background of the equatorial grid.
Look in the direction towards which Earth is moving: RA 1h 20m 9.92s Dec +8° 27′ 9.39″ (-X axis of chase frame) RA 1h 20m 2.53s Dec +8° 26′ 22.21″ (direct measurement)Do the chase frame exercise in “List the Retrograde Rotators” (listRetrogrades).
Now let’s look down at the Earth’s leading hemisphere—the one that intercepts the most meteoroidsmeteoroids (intercepted by Earth) as we orbit the Sun. We’ll display the Earth’s velocity vector, a bluish arrow that shows which way the Earth is moving. It will point straight at the observer and stays there. The Earth’s orbit is the red line that remains anchored to the center of the Earth’s disk.
If the Earth’s orbit were a perfect circle, the plane of the terminatorterminator would always contain the velocity vector. But as we fast forward with the keys j, k, l, the plane moves slightly left and right.
--[[
Stay in front of the Earth as it moves around the Sun.
Look at its leading hemisphere, with the north pole of the ecliptic overhead.
Press j, k, l to speed up and slow down.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("ecliptic")
celestia:hidelabel("planets")
celestia:show("orbits")
--Show only the Earth's orbit.
celestia:setorbitflagsCelestia:setorbitflags({Moon = false, Planet = false})
local earth = celestia:find("Sol/Earth")
celestia:select(earth)
earth:addreferencemark({type = "velocity vector"}) --bluish
earth:addreferencemark({type = "sun direction"}) --yellow
earth:addreferencemark({ --Show the terminator as a yellow line.
type = "visible region",
target = celestia:find("Sol")
})
local chaseFrame = celestia:newframe("chase", earth)
observer:setframe(chaseFrame)
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
observer:setposition(chaseFrame:from(position))
observer:lookat(
chaseFrame:from(std.position0),
chaseFrame:from(-std.zaxis))
wait()
end
main()
Were you distracted by the furious rotation of the Earth at high speeds?
If so,
display snapshots at 24-hour intervals instead of a continuous movie.
First, hide the clouds.
celestia:hide("cloudmaps", "cloudshadows", "ecliptic")
Then change the
wait
to the following.
For the 24-hour interval,
see the
mean solar day
in
solarDays.
To see a velocity vector that lies farther from the plane of the terminator, pick a planet of greater orbital eccentricity. A good choice would be MarsMars, orbital eccentricity of.
Verify that the negative X axis of Pluto’s chase frame points towards Pluto’s direction of motion with respect to the Sun, and that Pluto’s bluish velocity vector points towards Pluto’s direction of motion with respect to the Pluto-Charon barycenter. What about the negative X axis and bluish velocity vector of the following “object”? local barycenter = celestia:find("Sol/Pluto-Charon") assert(type(barycenter) == "userdata" and tostring(barycenter) == "[Object]" and barycenter:type() == "invisible")
I sometimes think that Japetus has been flashing like a cosmic heliograph for three hundred years, and we’ve been too stupid to understand its message.…
The moons in the outer Solar System sweep up a lot of debris.
If a moon has a permanently leading hemisphere,
all of the intercepted material accumulates on it.
The classic example is
Saturn’s
moon
Iapetus,
whose leading hemisphere is covered with tar.
Other satellites with asymmetrical hemispheres are
Saturn’s moon
TethysTethys (moon of Saturn)
and
Uranus’s
moon
OberonOberon (moon of Uranus).
For the method
Observer:splitview,
see
Splitview.
--[[
Split the window into left and right views.
Display the leading (dark) and trailing (bright) hemispheres of Iapetus.
Speed up time with the keys j, k, l to watch day and night sweep across
the hemispheres.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "grid")
celestia:hidelabel("constellations", "moons")
celestia:setambient(1) --equal light on both hemispheres
celestia:setwindowbordersvisible(false) --Don't waste a single pixel.
local iapetus = celestia:find("Sol/Saturn/Iapetus")
iapetus:addreferencemark({type = "velocity vector"})
local chaseFrame = celestia:newframe("chase", iapetus)
observer:setframe(chaseFrame)
--[[
Divide the window into left and right views, with a one-pixel margin all
around each view. The dimensions in pixels of each view are
width / 2 - 2, height - 2.
]]
local width, height = celestia:getscreendimension()
local fov = math.min(
observer:gethorizontalfov(width / 2 - 2, height - 2),
observer:getverticalfov (width / 2 - 2, height - 2))
--How many multiples of the radius of Iapetus does the observer have to
--be from the center of Iapetus in order to fit Iapetus into the fov?
local multiples = 1 / math.sinmath.sin(fov / 2)
local microlightyears = multiples * iapetus:radius() / KM_PER_MICROLY
local hemisphere = {
{celestia:newposition(-microlightyears, 0, 0), "Leading"},
{celestia:newposition( microlightyears, 0, 0), "Trailing"}
}
observer:splitviewObserver:splitview("v") --"v" for vertical
local up = chaseFrame:from(-std.zaxis) --negative Z points north
for i, observer in ipairs(celestia:getobserversCelestia:getobservers()) do
observer:setposition(chaseFrame:from(hemisphere[i][1]))
observer:lookat(chaseFrame:from(std.position0), up)
end
--width in pixels of half the window, minus width of left view's text.
local n = width / 2 - celestia:gettextwidthCelestia:gettextwidth(hemisphere[1][2])
--Same distance, but measured in characters.
--This will be the distance between the two captions.
n = n / celestia:gettextwidth(" ")
local s = hemisphere[1][2] .. string.rep(" ", n) .. hemisphere[2][2]
celestia:print(s, math.huge, -1, -1, 1, 2)
wait()
end
main()
In
broadsideEllipse
we displayed the attractively proportioned orbit of
Nereid
around
Neptune.
Let’s compute the
inclinationinclination (orbital element)
and
ascending
nodeascending node (orbital element)
of the orbit,
instead of cribbing them from the
data/solarsys.ssc
file.
The plane of Neptune’s equator is the XZ plane of Neptune’s equatorial frame. The plane of Nereid’s orbit around Neptune is the XY plane of Nereid’s chase frame. The angle between these planes is Nereid’s orbital inclination. The intersection of the planes is the line of the nodes.
There’s an easy way to compute the angle and intersection. Consider the vectors perpendicular to the planes: the Neptune equatorial frame Y axis and the Nereid chase frame negative Z axis. (Negative to make it point up.) The angle between the vectors is the angle between the planes; the cross product of the vectors is the intersection of the planes. Damn elegant, wouldn’t you say? After all, the cross product is perpendicular to the Neptune equatorial frame Y axis, and therefore lies in that frame’s XZ plane. The cross product is also perpendicular to the Nereid chase frame negative Z axis, and therefore lies in that frame’s XY plane.
--[[
Print the inclination and ascending node of Nereid's orbit around Neptune.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
celestia:settime(2447763.5) --epoch from data/solarsys.ssc
local satellite = celestia:find("Sol/Neptune/Nereid")
local primary = satellite:getinfo().parent
--Neptune's axis of rotation in universal frame
local equatorialFrame = celestia:newframe("equatorial", primary)
local axis = equatorialFrame:from(std.yaxis)
--vector perpendicular to Nereid's orbit in universal frame
local chaseFrame = celestia:newframe("chase", satellite)
local normal = chaseFrame:from(-std.zaxis)
--vector from center of Neptune towards ascending node,
--converted to Neptune's equatorial frame
local toNode = equatorialFrame:to(axis ^ normal)
local longlat = toNode:getlonglat()
local s = string.format(
"inclination = %g%s\n"
.. "ascending node = %g%s",
math.deg(axis:angleVector:angle(normal)), std.char.degree,
math.deg(longlat.longitude), std.char.degree)
celestia:print(s, math.huge)
wait()
end
main()
The output agrees with Nereid’s elements
data/solarsys.ssc.
Print a table showing the
inclination
of each planet’s orbit
to the plane of the
ecliptic.
For the recursive method
Object:family,
see
Recursion.
Please treat
PlutoPluto, planetary status of
as a planet.
Object:family() do
if object:type() == "planet" or object:name() == "Pluto" then
Mercury 7.00607°
Venus 3.39675°
Earth 0°
Mars 1.85089°
Jupiter 1.30559°
Saturn 2.48913°
Uranus 0.774348°
Neptune 1.77011°
Pluto 17.0062°
After reading mercuryPerihelion, we will be able to find the time of Nereid’s periapsis before the epoch. This will let us compute two more of the orbital elements: the mean anomaly at the epoch, and the argument of the pericenter.
The radiant point of a meteor shower is the direction from which the meteors seem to approach an observer on Earth. For example, the radiant point of the annual Perseid meteor showerPerseid meteor shower is at RA 3h 4m Dec +58°, just north of the constellation Perseus. We can think of this direction as a vector pointing (ominously) towards us from Perseus. It is the sum of two other vectors: the vector giving the motion of the Earth through space, and the negative of the the vector giving the motion of the meteoroids. Let’s find these two vectors, add them together, and see if we get the radiant point.
Every year on approximately August 12th,
the Earth passes through the trail of meteoroids.
The negative X axis of the Earth’s chase frame then gives us the
earthDirection
vector in the following program.
The meteoroids follow the orbit of
comet
Swift-TuttleSwift-Tuttle (comet),
which we added to Celestia’s
data/comets.ssc
file in the exercises in
broadsideEllipse.
On March 5, 1990,
the comet was at approximately the point where
the Earth crosses the comet’s orbit every August 12th.
The negative X axis of the comet’s chase frame
gives us the
cometDirection
vector,
which is also the direction of the accompanying meteoroids
at that point in their orbit.
The comet and the Earth are moving at very different speeds
when their paths cross.
We therefore multiply
earthDirection
and the
cometDirection
by the speeds of their respective celestial objects
before we perform the vector addition.
--[[
Compute the radiant point of the Perseid meteor shower as seen from Earth.
Measure the speed of a celestial object by recording its position at two
consecutive calls to the tickHandler, and recording the interval of simulation
time between the calls.
]]
require("std")
--variables used by tickHandler:
local object = nil --earth or comet
local i = nil --make two consecutive calls to the tickHandler
local t = {} --table of times
local position = {} --table of positions
local function tickHandler()
if i == 1 then
t[object] = {}
position[object] = {}
end
t[object][i] = celestia:gettime()
position[object][i] = object:getposition()
if i == 1 then
i = i + 1
else
celestia:registereventhandler("tick", nil)
end
end
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
--Earth passes through trail of micrometeoroids along comet's orbit
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
celestia:settime(celestia:utctotdb(year, 8, 12))
local earth = celestia:find("Sol/Earth")
local earthFrame = celestia:newframe("chase", earth)
local earthDirection = earthFrame:from(-std.xaxis)
object = earth
i = 1
celestia:registereventhandler("tick", tickHandler)
wait(.1) --enough time to make two calls to the tickHandler
local dt = t[earth][2] - t[earth][1]
assert(dt > 0)
--microlightyears per day
local earthSpeed =
(position[earth][2] - position[earth][1]):length() / dt
--comet crosses plain of ecliptic going north to south
celestia:settime(celestia:utctotdb(1990, 3, 5, 2, 16, 11))
local comet = celestia:find("Sol/Swift-Tuttle")
local cometFrame = celestia:newframe("chase", comet)
local cometDirection = cometFrame:from(-std.xaxis)
object = comet
i = 1
celestia:registereventhandler("tick", tickHandler)
wait(.1)
dt = t[comet][2] - t[comet][1]
assert(dt > 0)
local cometSpeed =
(position[comet][2] - position[comet][1]):length() / dt
local computedRadiant =
earthSpeed * earthDirection - cometSpeed * cometDirection
--convert microlightyears per day into kilometers per second
local kmPerSec =
computedRadiant:length() * KM_PER_MICROLY / (60 * 60 * 24)
local realRadiant = celestia:newvectorradec(
math.rad((3 + 4 / 60) * 360 / 24),
math.rad(58))
local error = realRadiant:angle(computedRadiant)
local radecFrame = celestia:newframe("universal", std.radecRotation)
local longlat = radecFrame:to(computedRadiant):getlonglat()
local ra = std.tora(longlat.longitude)
local dec = std.todec(longlat.latitude)
--Look at the radiant point, with Polaris towards top.
assert(computedRadiant:length() > 0)
observer:lookat(
observer:getposition() + computedRadiant,
radecFrame:from(std.yaxis))
local s = string.format(
"Computed radiant point:\n"
.. "RA %dh %dm %.15gs\n"
.. "Dec %s%d%s %d%s %.15g%s\n"
.. "Error: %.15g%s\n"
.. "Speed: %.15g kilometers/second",
ra.hours, ra.minutes, ra.seconds,
std.sign(dec.signum), dec.degrees, std.char.degree,
dec.minutes, std.char.minute,
dec.seconds, std.char.second,
math.deg(error), std.char.degree,
kmPerSec)
celestia:mmprint(s)
wait()
end
main()
The computed radiant point is close to the Wikipedia radiant point of RA 3h 4m Dec +58°. The exact output depends on the interval between consecutive Celestia ticks.
MM Computed radiant point: RA 3h 3m 38.6465748892761s Dec +57° 40′ 36.4051614637106″ Error: 0.3266721366139° Speed: 59.4194270579473 kilometers/secondThe annual Leonid meteor showerLeonid meteor shower on November 15th is composed of debris that follow the orbit of comet Tempel-TuttleTempel-Tuttle (comet). Its radiant point is in Leo at approximately RA 10h 8m Dec +22°. Derive the radiant point as we did in the above program.
We assumed that on March 5, 1990, the comet was at the point where the Earth crosses Swift-Tuttle’s orbit every August 12th. After you have read findZero, compute this date for yourself. Find the time in March, 1990 when the comet crossed the plane of the ecliptic, i.e., the time when the comet’s y coördinate in the universal frame changed its sign.
our conclusions
Each pair of distinct celestial objects has a lock frame. The first object is called the reference object; the second is the target object. The observer is usually positioned near the reference object and looks towards the target object. The two objects do not necessarily have to be a satellite and its primary. They could be the Earth and Mars, for example, or Mars and Earth. But they could not be Earth and Earth.
The origin of the lock frame is the center of the reference object. The XY plane is the plane of the reference object’s motion with respect to the target object. Note that this frame’s fundamental plane is the XY, not the XZ. The X axis points towards the center of the target object. The negative Y axis points approximately in the direction of the reference object’s motion with respect to the target object, and the positive Y axis points towards were the reference object came from. More precisely, the Y axis is erected (erect) so that it lies in the XY plane and is perpendicular to the X axis. The Z axis is determined by the other two axes because all Celestia frames are right-handedright-handed frame; see framesOfReference. For the Earth and Sun, it points towards the north pole of the ecliptic in Draco. For the Sun and Earth, it points towards the same place.
Please do not make a lock frame for two objects that are motionless with respect to each other: Celestia wouldn’t know where to put the Y axis and would divide by zerodivision by zero. Do not make a lock frame for two objects that are moving directly towards or directly away from each other: the X and Y axes would be colinear.
Here is the distinctive axis of each of our last three frames of reference:
The sub-Earth point on the lunar surface wanders in a loop, a phenomena called libration. We saw a closeup of this rocking motion superimposed on Mare MarginisMare Marginis (lunar sea) in hesitantTerminator. Now let’s look at the entire sub-Earth hemisphere of the Moon.
The following program establishes a lock frame from the Earth to the Moon. The Earth is the reference object and the center of the Earth is the origin. The Moon is the target object, and the X axis goes through the sublunar point on the Earth’s surface, the sub-Earth point on the lunar surface, and the center of the Moon. The observer is positioned at the sublunar point on the Earth, looking towards the Moon with the lunar orbit horizontal. The sub-Earth point on the lunar surface, marked by a dull green “body to body” arrow, remains stationary in the center of the window as the Moon wobbles.
Viewed from above (i.e., from the north), the Moon orbits counterclockwise around a comparatively stationary Earth. If the Moon were our stationary reference point, the Earth would orbit counterclockwise around the Moon. This is why the Earth’s velocity vector with respect to the Moon points to the right in our program, causing the lock frame Y axis to point to the left. (The conspicuous bright green Y axis we see pointing rightwards out of the Moon is not the lock frame Y axis. It’s the negative Z axis of the Moon’s bodyfixed frame.)
--[[
Show the Moon's libration as seen from the sublunar point on Earth.
The lock frame X axis points into the window, towards the center of the Moon.
The Y axis points left, negative Y points right.
The Z axis points towards the top of the window, perpendicular to the plane of
the Moon's orbit.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setfov(math.rad(45 / 60)) --45 minutes of arc
celestia:hide("constellations", "ecliptic", "galaxies", "grid",
"markers")
celestia:hidelabel("galaxies", "moons", "stars")
local earth = celestia:find("Sol/Earth")
local moon = celestia:find("Sol/Earth/Moon")
celestia:select(moon)
moon:addreferencemark({type = "body axes"})
moon:addreferencemark({type = "planetographic grid"})
moon:addreferencemark({type = "body to body direction", target = earth})
--Earth is the reference object, Moon is the target object.
local lockFrame = celestia:newframe("lock", earth, moon)
observer:setframe(lockFrame)
local microlightyears =
(earth:radius() + earth:getinfo().atmosphereHeight)
/ KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
observer:lookat(moon:getposition(), lockFrame:from(std.zaxis))
--one sidereal month of simulation time per 20 seconds of real time
celestia:settimescale(moon:getinfo().orbitPeriod * 60 * 60 * 24 / 20)
wait()
end
main()
From the Sun’s point of view, the rotation of Mercury falters and then presses on. See solarDays for the computation of Mercury’s solar day, and hesitantTerminator for another view of Mercury’s rotation.
--[[
Hover over the subsolar point on Mercury and watch the planet do the Twist.
The lock frame X axis points up out of the window towards the Sun (to our rear).
Mercury's velocity vector points left, so the lock frame Y axis points right.
The lock frame Z axis points north, towards the top of the window.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "grid", "markers")
celestia:hidelabel("constellations", "galaxies", "nebulae", "planets",
"stars")
local sol = celestia:find("Sol")
local mercury = celestia:find("Sol/Mercury")
celestia:select(mercury)
mercury:addreferencemark({type = "sun direction"}) --yellow
mercury:addreferencemark({type = "planetographic grid"})
local lockFrame = celestia:newframe("lock", mercury, sol)
observer:setframe(lockFrame)
local microlightyears = 5 * mercury:radius() / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
--The up vector is perpendicular to Mercury's orbit around the Sun.
observer:lookat(
lockFrame:from(std.position0),
lockFrame:from(std.zaxis))
local info = mercury:getinfo()
local orbitPeriod = info.orbitPeriod --in Earth days
local rotationPeriod = info.rotationPeriod --in Earth days
--length in Earth days of one Mercurian solar day
assert(orbitPeriod ~= rotationPeriod)
local d = orbitPeriod * rotationPeriod / (orbitPeriod - rotationPeriod)
--One Mercurian solar day of simulation time (about 176 Earth days)
--per 12 seconds of real time.
celestia:settimescale(60 * 60 * 24 * d / 12)
wait()
end
main()
We saw in tailPoints that the gas tail of Halley’s Comet points away from the Sun. Let’s restate this in terms of the Halley-Sol lock frame. The nucleusnucleus of comet of the comet is at the origin and the tail extends along the negative X axis. The following program positions the observer on the Y axis, perpendicular to the tail.
--[[
Show a broadside view of the tail of Halley's comet, keeping the nucleus at the
center of the window.
The Halley-Sol lock frame X axis points left, towards the Sun (beyond the
window).
The Y axis points out of the window towards the user.
The Z axis points up. It's pointing south because Halley's orbital inclination
(162 degrees) is greater than 90 degrees.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hidelabel("comets") --We know that the comet is Halley's.
local halley = celestia:find("Sol/Halley")
celestia:select(halley)
--Marks too small to see unless we approach nucleus with Home key.
halley:addreferencemark({type = "sun direction"})
halley:addreferencemark({type = "velocity vector"})
local sol = celestia:find("Sol")
local lockFrame = celestia:newframe("lock", halley, sol)
observer:setframe(lockFrame)
--halley:radius() is radius of nucleus, in kilometers
local microlightyears = 5e5 * halley:radius() / KM_PER_MICROLY
local position = celestia:newposition(0, microlightyears, 0)
observer:setposition(lockFrame:from(position))
observer:lookat(
lockFrame:from(std.position0),
lockFrame:from(std.zaxis))
--a thousand days before perihelion
celestia:settime(celestia:utctotdb(1986, 2, 9) - 1000)
--32 days of simulation time per second of real time
celestia:settimescale(60 * 60 * 24 * 32)
wait()
end
main()
View the comet head-on.
--directly between the Sun and the comet. local position = celestia:newposition(microlightyears, 0, 0)
Better yet, display the broadside and head-on views simultaneously,
using a
splitview
like the one in
Iapetus.
Did the Earth pass through the tail of Halley’s comet on May 19, 1910 in the Celestia universe? What was the Earth’s position with respect to the Sol-Halley lock frame during that day? When was it closest to the X axis?
We used a lock frame in settime to watch the Earth during a solar eclipse. Now let’s look at the Moon. The following program positions the observer at the point of perpetual total solar eclipse: the vertex (tip) of the Moon’s umbraumbra (of Moon).
The umbra lies along the negative X axis of the Moon-Sun lock frame, with the vertex at a constantly changing distance from the origin. To compute the distance, let R and r be the radii in kilometers of the Sun and Moon, and d the distance in kilometers between their centers. Let u be the length in kilometers of the umbra, from the center of the Moon to the vertex. We can find this u by setting up similar triangles:
r R = u d + uSolving for u yields
u = dr R − r
In the program,
d
is
distance
and
u
is
umbraLength.
Note that
main
cannot call
Observer:lookat,
because the observer’s position has not yet been set.
Can you see
Baily’s
pixelsBaily’s beads?
--[[
Station the observer at the point of perpetual total solar eclipse:
the vertex of the Moon's umbra.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local sol = celestia:find("Sol")
local moon = celestia:find("Sol/Earth/Moon")
local lockFrame = celestia:newframe("lock", moon, sol)
local R = sol:radius()
local r = moon:radius()
assert(R > r, "Moon's umbra is of infinite length.")
local factor = r / (R - r)
local function tickHandler()
local distance = moon:getposition():distanceto(sol:getposition())
local umbraLength = distance * factor
local position =
celestia:newposition(-umbraLength / KM_PER_MICROLY, 0, 0)
observer:setposition(lockFrame:from(position))
--Lunar disc spans one third of the vertical field of view.
local angularRadius = math.asin(r / umbraLength)
local angularDiameter = 2 * angularRadius
observer:setfovObserver:setfov(3 * angularDiameter)
local s = string.format(
"Moon to Sun: %.0f kilometers\n" --whole number, no fraction
.. "Moon to observer: %.0f kilometers\n"
.. "Angular diameter of Moon: %g%s",
distance, umbraLength,
math.deg(angularDiameter) * 60, std.char.minute)
celestia:print(s)
end
local function main()
celestia:hide("constellations", "ecliptic", "galaxies", "grid")
celestia:hidelabel("constellations", "galaxies", "moons", "nebulae",
"planets", "stars")
observer:setframe(lockFrame)
--Look along the X axis, towards x = infinity,
--with the Z axis pointing up.
local orientation = celestia:newrotationforwardup(std.xaxis, std.zaxis)
observer:setorientation(lockFrame:from(orientation))
--one sidereal month of simulation time per 30 seconds of real time
celestia:settimescale(60 * 60 * 24 * moon:getinfo().orbitPeriod / 30)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Moon to Sun: 147242569 kilometers
Moon to observer: 368504 kilometers
Angular diameter of Moon: 32.4187′
Position the observer at the vertex of
SaturnSaturn, oblateness of’s
umbra.
Quite aside from its rings,
you can admire its
oblateness.
Also try the
asteroid
"Sol/1620 Geographos"Geographos (asteroid).
SaturnSaturn, Lagrangian points of’s moons TethysTethys (moon of Saturn), TelestoTelesto (moon of Saturn), and CalypsoCalypso (moon of Saturn) fly in formation. The latter two remain stationed at the L4L4 (Lagrangian point) and L5L5 (Lagrangian point) Lagrangian points of Saturn and Tethys. Let’s fly with them, matching their course and speed.
The plane of the orbit is the XY plane of the Saturn-Tethys lock frame.
The angles between the satellites
are differences of longitude in this plane,
staying constant at approximately
60°.
The angles have to be measured with
Position:getlonglatPosition:getlonglat,
not with the dot product
or
Vector:angleVector:angle,
because we want the sign of the angle as well as its size:
Tethys is ahead, Callypso behind.
The longitude returned by
getlonglat
is in the range 0 to almost
2π.
We subtract
2π
to get it into the range
–π
to almost
π.
One complication:
we want to print the longitude of the
position
in the XY plane,
but
getlonglat
measures longitude in the XZ plane.
We therefore copy the coördinates of the
position
into a
newPosition,
swapping the
y
and
z.
We also negate the third coördinate
because the Y axis points “up”
in the XY plane,
while the Z axis points “down” in the XZ plane.
The first four arguments we give to
Object:markObject:mark
are the default values taken from the C++ function
object_mark
in
version/src/celestia/celx_object.cpp.
In
equalArea
we will mark the Lagrangian points themselves,
not the satellites that approximate their positions.
--[[
Fly in formation with Saturn's moon Tethys and its L4 and L5 Lagrangian points.
The satellites' orbit lies in the plane of the window.
The observer is north of the plane, looking south.
Saturn remains stationary at the bottom center, Tethys at the top center.
The midpoint between them is at the center of the window.
Telesto (L4) is on the left, Calypso (L5) on the right.
The X axis of the Saturn-Tethys lock frame points towards the top of the window.
Tethy's velocity vector points left, so Saturn's points right.
The Y axis therefore points left.
The Z axis points out of the window towards the user.
]]
require("std")
--variables used by tickHandler:
--the two large masses:
local M1 = celestia:find("Sol/Saturn")
local M2 = celestia:find("Sol/Saturn/Tethys")
--objects occupying the Lagrangian points
local L = {
[4] = "Sol/Saturn/Telesto",
[5] = "Sol/Saturn/Calypso"
}
local lockFrame = celestia:newframe("lock", M1, M2)
local direction = {[true] = "ahead of", [false] = "behind"}
local function tickHandler()
local s = ""
for i = 4, 5 do
local position = lockFrame:to(L[i]:getposition())
local newPosition = celestia:newposition(position:getx(),
position:getz(), -position:gety())
local longitude = newPosition:getlonglat().longitude
if longitude >= math.pi then
longitude = longitude - 2 * math.pi
end
s = s .. string.format(
"%s (L%d) is %g%s %s %s.\n",
L[i]:name(), i, math.deg(math.abs(longitude)),
std.char.degree, direction[longitude >= 0], M2:name())
end
celestia:print(s)
end
local function main()
local observer = celestia:sane()
celestia:select(M2)
celestia:hide("constellations", "ecliptic", "grid")
celestia:hidelabel("constellations")
celestia:showlabel("minormoons")
celestia:setorbitflagsCelestia:setorbitflags({MinorMoon = true, Planet = false})
celestia:show("orbits")
observer:setframe(lockFrame)
local microlightyears = lockFrame:to(M2:getposition()):getx()
local position = celestia:newposition(0, 0, 2 * microlightyears)
observer:setposition(lockFrame:from(position))
--Look at midpoint between Saturn and Tethys.
local target = celestia:newposition(microlightyears / 2, 0, 0)
observer:lookat(lockFrame:from(target), lockFrame:from(std.xaxis))
for i = 4, 5 do
L[i] = celestia:find(L[i])
L[i]:mark("green", "diamond", 10, .9, "L" .. i)
end
--One M2 orbit (about 2 Earth days) per 60 seconds of real time
celestia:settimescale(60 * 60 * 24 * M2:getinfo().orbitPeriod / 60)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Telesto (L4) is 57.4476° ahead of Tethys.
Calypso (L5) is 60.3923° behind Tethys.
Change
Sol/Saturn/Tethys
Sol/Saturn/Telesto
(L4)
Sol/Saturn/Calypso
(L5)
to
Sol/Saturn/Dione
Sol/Saturn/Helene
(L4)
Sol/Saturn/Polydeuces
(L5)
which enjoy the same relationship.
Let’s watch a transit of Venustransit of Venus. We will use a Earth-Sol lock frame to keep the observer above the Earth’s subsolar point. Venus’s phase angle will approach 180°.
--[[
Watch the June 6, 2012 transit of Venus from the top of the atmosphere
at the Earth's subsolar point. Keep the ecliptic horizontal.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("grid")
celestia:show("eclipticgrid")
celestia:hidelabel("planets") --We know that Venus is Venus.
local sol = celestia:find("Sol")
local venus = celestia:find("Sol/Venus")
local earth = celestia:find("Sol/Earth")
celestia:select(venus)
local lockFrame = celestia:newframe("lock", earth, sol)
observer:setframe(lockFrame)
local microlightyears =
(earth:radius() + earth:getinfo().atmosphereHeight)
/ KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
--ecliptic horizontal
observer:lookat(sol:getposition(), lockFrame:from(std.zaxis))
--Make the Sun span half the vertical field of view.
local distance = observer:getposition():distanceto(sol:getposition())
local angularRadius = math.asin(sol:getinfo().radius / distance)
local angularDiameter = 2 * angularRadius
observer:setfov(2 * angularDiameter)
--about 5 hours before the transit begins
celestia:settime(celestia:utctotdb(2012, 6, 5, 16))
--6 hours of simulation time (the duration of the transit)
--per 30 seconds of real time
celestia:settimescale(60 * 60 * 6 / 30)
wait()
end
main()
Did the 2012 transit take place at Venus’s ascending nodeascending node (orbital element) (broadsideEllipse) or descending node?
Turn the
"grid"
back on to read the right ascension of the Sun as seen from the Earth
during the transit.
Does it agree with the
76.681°
longitude of
the ascending node
given for Venus in the comment in
data/solarsys.ssc?
Add a tick handler to print the angular distance between the centers of the Sun and Venus as seen by the observer. Announce the four contactscontact (of transit) of the transit.
There will be simultaneous transits of Mercury and Venus
on July 26, 69163 A.D. in the Wikipedia universe.
Unfortunately,
no transit occurs at that time in the Celestia universe.
But perhaps Celestia has simultaneous transits in store for us at other times.
Write a program that searches for them,
in the future and in the past.
You’ll need the
std.zero
function in
findZero.
The user looks at the simulated universe through a window made of rows and columns of pixels. The pixel at the center of the window marks the direction in which he is looking. In this section, this pixel will be denoted (0, 0). The x values increase to the right, the y values upwards.
Given a position in the simulated universe,
at what pixel in the window would that position be displayed?
The answer is returned by the standard library method
Observer:getscreencoordinatesObserver:getscreencoordinates,
which projects the three-dimensional Celestia simulation space
onto the two-dimensional window.
It accepts a
Position
object in universal coördinates,
which will often be the center of a celestial object.
It returns the
(x, y)
coördinates, possibly with fractions, of the pixel
where that position would be displayed in the window,
assuming that no celestial objects are blocking the observer’s view of it.
The return values will be
(nilnil (Lua value),
nil)
if the position is not visible in the window,
i.e., if it is behind the observer.
The method assumes that the window has not been split with
Observer:splitviewObserver:splitview.
The following diagrams illustrate how
Observer:getscreencoordinates
works.
The first picture shows the observer in simulation space
in the initial orientation,
looking parallel to the negative Z axis
with the Y axis pointing up.
A celestial object of interest is in front of him and slightly above.
The vector
v
points from the observer to the object,
tilting upwards at an angle of
θ.
We can compute
θ
with the
tangenttangent (trig function)
function.
The next diagram shows the user in real space. The vertical line at left is the plane of the window, seen edge-on. The height h is the height in pixels of the window; the fov is the angle of the user’s vertical field of view. From these values, the tangent function gives us the distance d in pixels that the user would have to be from the center of the window in order to have the given field of view. We want the user in real space to see exactly the same picture as the observer in simulation space, so the following θ has to be the same angle as the θ in the previous diagram. From d and θ, we can derive the vertical distance in pixels from the center of the window to the pixel where the position is displayed.
The points and lines that we draw can be attached to different anchors. In the following four sections, we attach them to the surface of the celestial sphere, to the surface of the window, to one of Celestia’s frames of reference, and to the surface of a celestial object. There are many other possibilities.
Read
Observer:getscreencoordinates
in the standard library file
std.lua in
stdCelx.
For simplicity,
assume that observer is in the initial orientation
std.orientation0,
to keep his direction of view horizontal.
Let’s draw a loop on the celestial sphere
tracing the
retrograde motion
of
MarsMars, retrograde motion of.
Run the Celx program in
retrogradeMars
that showed Mars moving back and forth.
At the same time,
run the following
renderoverlay
hook
(luaHookFunctions)
to trace the position of Mars on the celestial sphere.
When we drag on the sky to change the observer’s orientation,
the loop that the hook draws will move with the sky.
The loop will adhere to the surface of the celestial sphere
like the grid of right ascension and declination.
The values used by the hook
are stored as fields in the Lua hook table.
One of these values is the table of celestial objects to be traced.
For the time being,
this table will contain only one object,
Mars.
The table gives the color and alpha level of the object.
It also contains an array of vectors
showing the direction from the observer to the celestial object
at the time of each call to
renderoverlay.
Each vector indicates a point on the observer’s celestial sphere.
The length of the vector is irrelevant,
as long as it’s greater than zero.
Each time the hook is called,
a vector is added to the end of the array.
The expression
#data.vectors
is the number of vectors
and is therefore the subscript of the last vector in the array.
We will be reckless and not worry about running out of memory.
Warning: the method
Celestia:getscreendimensionCelestia:getscreendimension
returns the wrong width and height between calls to the functions
gl.Begin
and
gl.End.
Since
Celestia:getscreendimension
is called by
Celestia:getscreencoordinates,
we will have to make all our calls to the latter
before
the
gl.Begin.
The resulting screen coördinates are stored into the temporary array
temp.
Remember to add the
LuaHook
parameter to the
celestia.cfg
file
(luaHookFunctions).
--[[
This file is luahook.celx.
Draw the line that Mars makes, as seen by the observer.
]]
celestia:setluahook {
observer = nil,
objects = {}, --table of celestial objects to be traced
--Put the celestial object into the table of objects to be traced.
trace = function(self, object, red, green, blue, alpha)
assert(type(object) == "userdata"
and tostring(object) == "[Object]"
and type(red) == "number"
and type(green) == "number"
and type(blue) == "number"
and type(alpha) == "number")
self.objects[object] = {
red = red,
green = green,
blue = blue,
alpha = alpha,
vectors = {} --array of vectors from observer to object
}
end,
--Remove the object from the table of objects to be traced.
untrace = function(self, object)
assert(type(object) == "userdata"
and tostring(object) == "[Object]")
self.objects[object] = nil
end,
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
end
--Don't draw anything until the Celx program with the main
--function has increased the timescale.
if celestia:gettimescale() == 1 then
return
end
if self.observer == nil then
--[[
This is the first call to renderoverlay since the Celx
program set the timescale. Arguments of trace are rgb
alpha. Mars's rgb vales taken from data/solarsys.ssc.
]]
self.observer = celestia:getobserver()
self:trace(celestia:find("Sol/Mars"), 1, .75, 0.7, 1)
end
for object, data in pairs(self.objects) do
--a vector from the observer to the object
local v = object:getposition()
- self.observer:getposition()
--If this vector is different from the last vector (if
--any) in the array, append this vector to the array.
if v:length() > 0 then
local n = #data.vectors
if n == 0 or v:getx() ~= data.vectors[n]:getx()
or v:gety() ~= data.vectors[n]:gety()
or v:getz() ~= data.vectors[n]:getz()
then
table.inserttable.insert(data.vectors, v)
end
end
if #data.vectors > 0 then
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
local width, height =
celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
--Let the pixel in the center of the window
--be (0, 0).
gl.Translate(width / 2, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA,
gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING)
gl.Disable(gl.TEXTURE_2D)
if celestia:getrenderflags().smoothlines then
gl.Enable(gl.LINE_SMOOTH) --antialiasing
gl.LineWidth(1.5)
end
gl.Color(data.red, data.green, data.blue,
data.alpha)
local temp = {}
for i, v in ipairs(data.vectors) do
local position =
self.observer:getposition() + v
local x, y = self.observer
:getscreencoordinates(position)
if x ~= nil and y ~= nil then
table.insert(temp, {x, y})
end
end
gl.Begin(gl.LINE_STRIPgl.LINE_STRIP)
for i, xy in ipairs(temp) do
gl.Vertex(xy[1], xy[2])
end
gl.End()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
end
end
end
}
I wish the above call to
gl.Vertex
could have been
gl.Vertex(table.unpacktable.unpack(xy))
but Lua 5.1 does not have
unpack.
Don’t let
the
vectors
array grow until memory is exhausted.
Call
table.insert
only if
#data.vectors
is less than 10,000.
See also the
"count"
argument of the Lua function
collectgarbagecollectgarbage (Lua function).
Draw the
loopsdeferent, Ptolemaic
produced by the
deferents
and epicyclesepicycle, Ptolemaic
of the
Ptolemaic
solar systemPtolemaic solar system.
Run the Celx program in
tychoSolar
with the above
luahook.celx.
Trace each planet in a different color.
(Don’t trace the Earth—it doesn’t move.)
Press l
(lowercase L)
once to speed up the time.
Run the Celx program in tychoSolar again, but this time keep NeptuneNeptune, resonance with Pluto of motionless while you trace PlutoPluto, resonance with Neptune of. Admire their 2:3 orbital resonanceresonance, orbital.
The orbits of these planets are slower and bigger,
so you’ll have to speed up time
and position the observer farther from the plane of
the Solar System.
Get the radii of the orbits from the comments in
data/solarsys.ssc.
Better yet, compute the radii using
Kepler’s
third lawKepler’s third law.
It’s very simple to do:
math.pow(n / e, 2 / 3)
local microlightyears = astronomicalUnits * 1e6 / std.auPerLy
--Show Pluto's orbit, but not the orbit of any other dwarf planet.
for level, object in celestia:find("Sol"):familyObject:family() do
if object:type() == "dwarfplanet" --lowercase
and object:name() ~= "Pluto" then
object:setorbitvisibilityObject:setorbitvisibility("never")
end
end
celestia:setorbitflagsCelestia:setorbitflags({DwarfPlanet = true}) --two uppercase letters
Another way to visualize orbital resonance is in Corkscrew.
For several months in 1985 and 1986, the New York Times published a daily note on the progress of Halley’s CometHalley’s Comet, path projected onto celestial sphere. Each article consisted of a circular map of diameter 50°—a little porthole—centered on an X marking the comet’s position on the celestial sphere for that night. A dashed line through the X showed the past and future “Path of Halley’s Comet”. In those pre-Internet days, we would clip and collect the maps as souvenirs.
But I digress. Trace the path of the comet with Celestia during the year of its 1986 perihelion.
Adhere the observer to the Sun’s ecliptic frame. Trace the path of the Solar System Barycenter as it loops in and out of the Sun.
If a traced object goes out of the window and then comes back in,
our
renderoverlay
hook draws a straight line from the pixel where the object disappeared
to the pixel where it reappeared.
To correct this,
have the hook remember whether the object was in or out of the window
at the time of the previous call to the hook.
The Celx program in
supergalacticCoordinates
plotted the supergalactic equator on the celestial sphere in a very crude way.
We can now draw the equator as a clean straight line with the
renderoverlay
hook.
Add two new fields,
supergalacticFrame
and
vectors
to the table of Lua hooks after the
observer
field.
observer = nil, --existing field
supergalacticFrame = nil, --new fields
vectors = {},
Initialize the new field after initializing the
observer.
Don’t wait for a change in the time scale.
self.observer = celestia:getobserver()
self.supergalacticFrame = celestia:newframe("universal",
std.supergalacticRotation)
for i = 0, 360 do --or 359 with a gl.Begin(gl.LINE_LOOPgl.LINE_LOOP)
local v = celestia:newvectorlonglat(
math.rad(i),
math.rad(0))
table.insert(self.vectors,
self.supergalacticFrame:from(v))
end
Institute a supergalactic color.
gl.Color(0, 1, 1, 1) --cyan
And remember that we are now looping through
self.vectors,
not
data.vectors.
for i, v in ipairs(self.vectors) do
Why does the
for
loop count by ones to 360 instead of by twos?
for i = 0, 360, 2 do --count by twos
Hint: does the supergalactic equator go all the way to the edge of the window?
Invent a new grid analogous to the right ascension and declination grid. For example, draw the grid of supergalactic coördinates, or a grid whose north pole is the “hot spot” of the cosmic background microwave radiation in twoStars.
The four biggest satellites of JupiterJupiter, corkscrew diagram of satellites of are the Galilean moonsGalilean moons of Jupiter: IoIo (moon of Jupiter), EuropaEurop (moon of Jupiter), GanymedeGanymede (moon of Jupiter), and CallistoCallisto (moon of Jupiter), in order of increasing distance from their primary. Let’s plot their orbits using the vertical dimension to represent the passage of time. The resulting corkscrews will highlight the 1:2:4 orbital resonanceresonance, orbital of Io, Europa, and Ganymede.
--[[
This file is luahook.celx.
Trace the Galilean satellites of Jupiter on the surface of the window.
]]
celestia:setluahook {
commence = false,
observer = nil,
objects = {}, --table of celestial objects to be traced
--Put the celestial object into the table of objects to be traced.
trace = function(self, object, red, green, blue, alpha)
assert(type(object) == "userdata"
and tostring(object) == "[Object]"
and type(red) == "number"
and type(green) == "number"
and type(blue) == "number"
and type(alpha) == "number")
self.objects[object] = {
red = red,
green = green,
blue = blue,
alpha = alpha,
xys = {} --array of little arrays, each holding x and y
}
end,
--Remove the object from the table of objects to be traced.
untrace = function(self, object)
assert(type(object) == "userdata"
and tostring(object) == "[Object]")
self.objects[object] = nil
end,
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
end
--[[
Don't draw anything until the Celx program with the main
function has increased the timescale. But once started, keep
running even after the timescale has gone back to 1.
]]
if celestia:gettimescale() > 1 then
self.commence = true
elseif not self.commence then
return
end
if self.observer == nil then
--[[
This is the first call to renderoverlay since the Celx
program set the timescale. Trace the moons in red,
orange, yellow, green.
]]
self.observer = celestia:getobserver()
self:trace(celestia:find("Sol/Jupiter/Io"), 1, 0, 0, 1)
self:trace(celestia:find("Sol/Jupiter/Europa"),
1, .5, 0, 1)
self:trace(celestia:find("Sol/Jupiter/Ganymede"),
1, 1, 0, 1)
self:trace(celestia:find("Sol/Jupiter/Callisto"),
0, 1, 0, 1)
end
for object, data in pairs(self.objects) do
--a vector from the observer to the object
local position = object:getposition()
local x, y =
self.observer:getscreencoordinates(position)
--If this (x, y) is different from the last (x, y) (if
--any) in the array, append this (x, y) to the array.
if x ~= nil and y ~= nil then
local n = #data.xys
if n == 0 or x ~= data.xys[n][1]
or y ~= data.xys[n][2] then
table.inserttable.insert(data.xys, {x, y})
end
end
if #data.xys > 0 then
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
local width, height =
celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
gl.Translate(width / 2, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA,
gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING)
gl.Disable(gl.TEXTURE_2D)
if celestia:getrenderflags().smoothlines then
gl.Enable(gl.LINE_SMOOTH) --antialiasing
gl.LineWidth(1.5)
end
gl.Color(data.red, data.green, data.blue,
data.alpha)
gl.Begin(gl.LINE_STRIPgl.LINE_STRIP)
for i, xy in ipairs(data.xys) do
gl.Vertex(xy[1], xy[2])
end
gl.End()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
end
end
end
}
Jupiter and its retinue are initially along the top edge of the window.
As the program runs,
the observer pitches upwards to make Jupiter travel down
to the bottom edge.
During each day of simulation time,
Jupiter moves
height/days
pixels down the window,
where
height
is the height of the window in pixels
and
days
is the total number of days of simulation time.
Thus Jupiter descends a total of
height
pixels,
going from an altitude of
height/2
above the center of the window to
–height/2
above the center.
The variable
pixels
holds this vertical distance.
theta
is the angle through which the observer has to be pitched up or down
to place Jupiter at the correct altitude
above or below the center of the window.
The angle is measured from the line that connects the observer to Jupiter.
theta
depends on the aforementioned vertical distance in
pixels.
It also depends on the horizontal distance from the user to the window.
Our standard assumption is that he or she
is 400 millimeters from the center of the
window.
If the user approaches the window,
the window affords him or her a wider field of view.
If the user recedes,
it affords him or her a narrower field of view.
Since our field of view is very narrow (only half of a degree),
the user must be a great distance from the window.
This distance is in the variable
distance.
--[[
This is the file that holds the main function.
Draw a corkscrew graph of Jupiter's Galilean satellites. The observer stays at
the sub-Jupiter point on Earth, zoomed in on Jupiter with a narrow field of
view. Jupiter's equator remains horizontal.
Jupiter initially appears at the center of the top edge of the window. The
observer pitches up so that Jupiter ends up at the center of the bottom edge.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local days = 10 --duration in Earth days that the diagram should cover
local width, height = celestia:getscreendimension()
local pixelsPerDay = height / days
local t0 = celestia:gettime()
local jupiter = celestia:find("Sol/Jupiter")
--Keep the plane of Jupiter's equator horizontal.
local equatorialFrame = celestia:newframe("equatorial", jupiter)
local function tickHandler()
local t = celestia:gettime() - t0
if t >= days then
celestia:registereventhandler("tick", nil)
celestia:settimescale(1)
return
end
--Look at Jupiter, with its equator horizontal.
local orientation = observer:getposition():orientationtoPosition:orientationto(
equatorialFrame:from(std.position0),
equatorialFrame:from(std.yaxis))
--[[
How many pixels above or below center of window should Jupiter be?
When t == 0, pixels is height/2 (top edge of window).
When t == days/2, pixels is 0 (center of window).
When t == days, height is -height/2 (bottom edge of window).
]]
local pixels = (1 - 2 * t / days) * height / 2
--To get the narrow field of view, the user must be this distance in
--pixels from the center of the screen.
local distance = height / (2 * math.tanmath.tan(observer:getfovObserver:getfov() / 2))
--Pitch the observer up by an angle of theta
--to make Jupiter go down the window.
local theta = math.atan2math.atan2(pixels, distance)
local rotation = celestia:newrotation(std.xaxis, theta)
observer:setorientationObserver:setorientation(rotation * orientation)
end
local function main()
celestia:hide("grid")
celestia:show("lightdelay"lightdelay (renderflag)) --turned off by default
celestia:hidelabel("planets") --We know that Jupiter is Jupiter.
--The Moon occasionally blocks the observer's view of Jupiter.
celestia:find("Sol/Earth/Moon"):setvisible(false)
--Show only the Galilean satellites.
celestia:find("Sol/Jupiter/Amalthea"):setvisible(false)
local earth = celestia:find("Earth")
celestia:select(jupiter)
--Keep the observer above the sub-Jupiter point on Earth.
local lockFrame = celestia:newframe("lock", earth, jupiter)
observer:setframe(lockFrame)
local microlightyears =
(earth:radius() + earth:getinfo().atmosphereHeight)
/ KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
--Set horizontal field of view wide enough to encompass Callisto,
--the farthest Galilean moon.
local a = 1883000 --Callisto semimajor axis in km from data/solarsys.ssc
local distance =
observer:getposition():distanceto(jupiter:getposition())
--angular diameter of Callisto's orbit, seen from Earth
local angularRadius = math.asinmath.asin(a / distance)
local angularDiameter = 2 * angularRadius
observer:sethorizontalfov(1.05 * angularDiameter) --margin
celestia:registereventhandler("tick", tickHandler)
--Galileo sees the Galilean satellites for the first time: Padua,
--January 7, 1610, "in the first hour of the night".
--celestia:settime(celestia:utctotdb(1610, 1, 7, 17))
--the specified number of days of simulation time
--per 30 seconds of real time
celestia:settimescale(60 * 60 * 24 * days / 30)
wait()
end
main()
The Solar System has many other resonances you could trace.
Consider the
2:3
resonance of
Neptune
and
Pluto,
or the
3:4
resonance of
Saturn’s
satellites
Titan
and
Hyperion.
Outside the Solar System, try the
1:2
resonance of the planets
Gliese 876/c
and
Gliese 876/b.
To confirm that the
lightdelay
renderflag is on,
look for the
LT
(“Light Travel”)
in the upper right corner of the window.
Could you show the user how much of a difference
is caused by the delay?
In 1676,
Ole
RømerRømer, Ole
used this difference to estimate the
speed
of lightlight, speed of.
Trace a yellow line along the
analemma
in
Analemma.
Also replace the column of M’s
with a white line down the middle of the window.
Which method should the
main
function call first,
Celestia:registereventhandler
or
Celestia:settimescale?
Should there be a
wait
between these calls?
[Time exposuretime exposure.]
Attach a camera to the ground,
aim it at
PolarisPolaris,
and leave the shutter open all night.
First, call
Observer:gethorizontalfov
and
Observer:getverticalorizontalfov
to get the observer’s horizontal and vertical field of view;
let
θ
be whichever angle is bigger.
Then trace the 30 stars of the brightest apparent magnitude
(loopDatabase)
that are within
θ/2
of the north celestial pole.
Get the color of each star from the exercise in
hertzsprungrussell.
At one of the lower corners of the window, sketch the traditional tree. See The Algorithmic Beauty of PlantsAlgorithmic Beauty of Plants, The (Prusinkiewicz and Lindenmayer) by Przemyslaw PrusinkiewiczPrusinkiewicz, Przemyslaw and Aristid LindenmayerLindenmayer, Aristid.
In the following examples, the lines are attached to points in Celestia’s three-dimensional simulation space.
The first program in
broadsideEllipse
gave us a broadside view of
NereidNereid (moon of Neptune)
going around its elliptical orbit.
Run it with the following
luahook.celx
to
illustrate Kepler’s
second
law,
the law of
equal
areas.
It draws straight line segments from
NeptuneNeptune
to Nereid
at equal intervals of time.
The segments are anchored to Neptune
and to points along the ellipse of the orbit;
they remain at constant locations with respect to
Neptune’s
equatorial frame.
To see the resuling harp or spider web in three dimensions, rotate the observer around Nereid. Option-drag on the sky in Mac, right-drag in Microsoft Windows.
--[[
This file is luahook.celx.
Illustrate Kepler's Equal Area Law by drawing straight line segments from the
primary to the satellite at equal intervals of time. The lines are anchored to
the primary's equatorial frame.
]]
celestia:setluahook {
n = 20, --number of line segments to draw
positions = {}, --array of Nereid endpoints of segments
t0 = nil, --The first orbitPeriod starts at time t0.
observer = nil,
nereid = nil,
primary = nil,
orbitPeriod = nil,
equatorialFrame = nil,
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
end
--Don't draw anything until the main function has set the
--timescale.
if celestia:gettimescale() == 1 then
return
end
if self.t0 == nil then
--This is the first call to renderoverlay
--since the main function set the timescale.
self.t0 = celestia:gettime()
self.observer = celestia:getobserver()
self.nereid = celestia:find("Sol/Neptune/Nereid")
local info = self.nereid:getinfo()
self.primary = info.parent
self.orbitPeriod = info.orbitPeriod
self.equatorialFrame = celestia:newframe("equatorial",
self.primary)
end
--[[
Draw the lines during only the first orbitPeriod.
Divide the orbitPeriod into self.n equal intervals.
The integer i tells which interval we're in now,
1 <= i <= self.n.
]]
local dt = celestia:gettime() - self.t0
if dt < self.orbitPeriod then
local i = 1 + math.floor(self.n * dt / self.orbitPeriod)
if self.positions[i] == nil then
local position = self.nereid:getposition()
self.positions[i] =
self.equatorialFrame:to(position)
end
end
if #self.positions == 0 then
return --The array is empty. No lines to draw yet.
end
--If the primary is not in the window, draw nothing.
local position = self.primary:getposition()
local xn, yn = self.observer:getscreencoordinates(position)
if xn == nil or yn == nil then
return
end
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
local width, height = celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
gl.Translate(width/2, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING)
gl.Disable(gl.TEXTURE_2D)
if celestia:getrenderflags().smoothlines then
gl.Enable(gl.LINE_SMOOTH) --antialiasing
gl.LineWidth(1.5)
end
gl.Color(1, 0, 0, 1) --rgba: SelectionOrbitColor from render.cpp
local temp = {}
for i, position in ipairs(self.positions) do
position = self.equatorialFrame:from(position)
local x, y =
self.observer:getscreencoordinates(position)
if x ~= nil and y ~= nil then
table.inserttable.insert(temp, {x, y})
end
end
gl.Begin(gl.LINESgl.LINES)
for i, xy in ipairs(temp) do
gl.Vertex(xy[1], xy[2])
gl.Vertex(xn, yn)
end
gl.End()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
end
}
Keep the color of the segments the same as the color of the orbitcolor, of orbit.
--rgb alpha. Colors from version/src/celengine/render.cpp. --Objects cannot be compared, but their names can be. if celestia:getselectionCelestia:getselection():name() == self.nereid:name() then
gl.Colorgl.Color(1, 0, 0, 1) --SelectionOrbitColor
else
gl.Color(0.08, 0.407, 0.392, 1) --MoonOrbitColor
end
Display a line segment from the Sun to the nucleus of Halley’s Comet in tailPoints. The line will move with the comet and verify that the tail always points away from the Sun.
Draw the positive X, Y, and Z axis of the bodyfixed frame we implemented for the Milky Way in alternativeBodyfixed. Don’t worry about the arrowheads.
Draw a square around the L4 and L5 Lagrangian points in Lagrangian. The plane of the square should be perpendicular to the line from the point to the observer.
Each year on
September
11th9/11 (September 11th),
the City of New York aims powerful searchlights straight up from the
site of the
World Trade Center.
Seen from a mile or two away,
the beams stretch from the horizon almost up to the zenith,
where they fade out near the star
Vega
in the early evening.
Can we simulate these lights in Celestia?
See
Object:setatmosphereObject:setatmosphere
and decide at what altitude they should fade out.
Attach them to the bodyfixed frame.
(From lower Manhattan there’s a strange effect,
but it’s visible only if you see it in person.
The beams follow a meridian of azimuth up the celestial sphere,
so they seem to bow towards us as they ascend.)
One of the iconic images of Western Science is Newton’s cannon on a mountaintopNewton’s cannon. It shoots a cannonball horizontally; with increasing initial speed, the ball travels farther around the earth until it goes into orbit. See the engraving facing page 6 in his Treatise of the System of the WorldTreatise of the System of the World (Newton) (1728).
After you have the “impulse power” technique in Impulse, trace the paths of the cannonballs in the engraving. Attach the paths to the bodyfixed frame. There is no need to use the scripted orbits in scriptedOrbit.
Draw the Roche lobesRoche lobes of a binary star system. Attach them to the lock frame.
In settime we watched a total solar eclipse sweep across Europe. Now let’s draw a line on the surface of the Earth tracing the path of totality. Run the program again, but hide the clouds and show the latitude and longitude lines.
--in the main function, after the call to Celestia:sane celestia:hide("cloudmaps", "cloudshadows") --in the main function earth:addreferencemark({type = "planetographic grid"})
The X axis of the Moon-Sun lock frame points from the Moon towards the Sun.
The negative X axis,
in the opposite direction,
is the axis of the Moon’s
umbraumbra (of Moon).
The following variable
far
tells how far the center of the Earth is from the axis of the umbra;
the distance is measured with the
Pythagorean
theoremPythagorean theorem.
If this distance is equal to the Earth’s radius,
the axis grazes the surface of the Earth at one point.
If this distance is less than the Earth’s radius,
the axis pierces the surface of the Earth at two points.
Of these two points,
p
is the one that is closer to the Moon.
(The
x
coördinate
of the center of the Earth is negative,
since the Earth is on the side of the Moon away from the Sun.
Adding a positive number to this
x
therefore moves us closer to the origin.
And the origin is the Moon.)
We convert
p
from the lock frame to the Earth’s bodyfixed frame,
via the universal frame,
and insert it into the array
self.positions.
The Earth is opaque,
so we don’t want to draw the points
on the side of the Earth away from the observer.
The
distanceToLimb
is the distance from the observer to any point on the
limb
(edge) of the
Earth.
The
distanceToPosition
is the distance from the observer to the point we want to plot.
If the distance to the point is less than the distance to the limb,
the point is on the visible side of the Earth and we draw it.
Since the equator is in cyan (rgb
(0, 1, 1)),
we pick a different color.
When the eclipse is over, rotate the Earth and admire how the path is printed on its surface. Option-drag on Mac, right-drag on Microsoft Windows.
--[[
This file is luahook.celx.
Trace the path of totality: the point on the surface of the Earth
on the axis of the Moon's umbra.
]]
celestia:setluahook {
commence = false,
observer = nil,
earth = nil,
lockFrame = nil, --negative X axis is axis of Moon's umbra
bodyfixedFrame = nil, --of Earth
radius = nil, --of Earth, in microlightyears
positions = {}, --array of Position objects in bodyfixedFrame
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
end
--[[
Don't draw anything until the Celx program with the main
function has increased the timescale. But once started, keep
running even after the timescale has gone back to 1.
]]
if celestia:gettimescale() == 1 then
self.commence = true
elseif not self.commence then
return
end
--This is the first call to renderoverlay
--since the Celx program set the timescale.
if self.observer == nil then
self.observer = celestia:getobserver()
self.earth = celestia:find("Sol/Earth")
self.lockFrame = celestia:newframe("lock",
celestia:find("Sol/Earth/Moon"),
celestia:find("Sol"))
self.bodyfixedFrame =
celestia:newframe("bodyfixed", self.earth)
self.radius =
self.earth:getinfo().radius / KM_PER_MICROLY
end
--How far is center of Earth from X axis of lockFrame?
local center = self.lockFrame:to(self.earth:getposition())
local far = math.sqrtmath.sqrt(center:gety()^2 + center:getz()^2)
if far <= self.radius then
--There is a position p where the axis of the umbra
--pierces the center of the Earth.
local microlightyears = center:getx()
+ math.sqrt(self.radius^2 - far^2)
local p = celestia:newposition(microlightyears, 0, 0)
p = self.lockFrame:from(p)
p = self.bodyfixedFrame:to(p)
table.inserttable.insert(self.positions, p)
end
if #self.positions == 0 then
return
end
local observerPosition = self.observer:getposition()
local distanceToCenter = observerPosition
:distanceto(self.earth:getposition()) / KM_PER_MICROLY
local temp = {}
for i, position in ipairs(self.positions) do
position = self.bodyfixedFrame:from(position)
local distanceToPosition =
observerPosition:distanceto(position)
/ KM_PER_MICROLY
local distanceToLimb =
math.sqrt(distanceToCenter^2 - self.radius^2)
if distanceToPosition <= distanceToLimb then
local x, y = self.observer
:getscreencoordinates(position)
if x ~= nil and y ~= nil then
table.insert(temp, {x, y})
end
end
end
if #temp == 0 then
return
end
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
local width, height = celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
gl.Translate(width/2, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING)
gl.Disable(gl.TEXTURE_2D)
if celestia:getrenderflags().smoothlines then
gl.Enable(gl.LINE_SMOOTH) --antialiasing
gl.LineWidth(1.5)
end
gl.Color(1, 0, 0, 1) --rgba: red
gl.Begin(gl.LINE_STRIPgl.LINE_STRIP)
for i, xy in ipairs(temp) do
gl.Vertex(xy[1], xy[2])
end
gl.End()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
end
}
Solar and lunar eclipses repeat themselves approximately every 18 years, a duration known as the sarossaros (eclipse cycle). Trace the paths of a pair of total solar eclipses separated by one saros. The first eclipse can be the 1999 eclipse in Europe that we just saw. The second eclipse comes 6585⅓ days later, in 2017. Because of the ⅓ the Earth will have rotated 120° to the east, and the shadow of the second eclipse will fall in North America.
--above the main function local t1 = celestia:utctotdb(2017, 8, 21, 20, 0, 0) --end of eclipse --in the main function local t0 = celestia:utctotdb(2017, 8, 21, 16, 50, 0) --start of eclipseThen shift the trace of the 2017 eclipse 120° to the east, moving it from North America to Europe. This should overlay the two paths. --immediately before the call to table.insert --in the renderoverlay hook local rotation = celestia:newrotation(std.yaxis, math.rad(-120)) p = rotation:transform(p) Is the shifted path of the 2017 eclipse almost the same as the path of the 1999 eclipse?
Our program suffers from the bug we saw in traceRetrograde. If the path of totality goes beyond the observer’s horizon and then comes back, the two visible parts of the path are joined by a straight line. Correct this.
We could illustrate an eclipse with much more elaborate graphics. For example, we could draw a loop around the area on the surface of the Earth where the eclipse is total at a given time. This exercise considers the problem of plotting the northernmost point on this loop.
It was comparatively easy to plot the point where the surface of the Earth is pierced by the axis of the umbra. The axis is “horizontal” because it lies along the X axis of the Moon-Sun lock frame. How could we plot the point where the surface is pierced by the ray from the top (i.e., northern limb) of the Sun to the top of the Moon? This ray slopes “downwards” because the Sun is bigger than the Moon. Although we can easily compute the angle of this slope, a tilted line is much harder to work with than a horizontal one.
The ray slopes because we measured it with respect to the Moon-Sun lock frame. Could we create a rotated version of this frame with respect to which the ray would be horizontal?
Trace the path of totality
and write the latitude and longitude in degrees of each point to an output file.
For the Lua standard output function
print,
see
standardOutput.
table.insert(self.positions, p) --existing statement
local longlat = p:getlonglat()
printprint (Lua function)(string.format("%.15g %.15g",
math.deg(longlat.latitude),
math.deg(longlat.longitude)
))
For our 1999 eclipse, the output would be the following.
The exact values depend on when the
renderoverlay
hook is called.
As the eclipse sweeps eastwards across the North Atlantic Ocean,
the east longitude increases towards
360°.
42.4477824211184 298.209299310384
42.8693731198955 299.759385143894
43.1857633454871 300.939263816394
etc.
Then draw the path in a
Google mapGoogle Maps
using the
PolylinePolylines (Google Maps)
class of the
Google
Maps JavaScript APIJavaScript
(Application Programming Interface).
The solar eclipse of January 24, 1925
was total in
New York City
north of West 96th Street,
and partial south of it.
(On the East Side, the cutoff street was 104th.)
Is Celestia accurate enough to simulate this?
Can we get a surface texture for the Earth
with enough detail to see the streets?
Visit the eclipse website at
tse1925.com
and prepare to launch the dirigibles.
The ancient Greek astronomer HipparchusHipparchus (190–120 BC) estimated the diameter of the Moon by means of a solar eclipse. It was total at the Hellespont on the north shore of the Mediterranean Sea, but covered only four fifths of the Sun’s diameter at Alexandria on the south shore. He concluded that the Moon was five times wider than the sea.
Let’s assume it was the eclipse at
local t = celestia:utctotdb(-128, 11, 20, 12, 54, 24) --129 BC
The
NASA solar eclipse page
shows part of the Hellespont lying within the path of totality;
see the map at
http://eclipse.gsfc.nasa.gov/SEsearch/SEsearchmap.php?Ecl=-01281120.
How accurately does Celestia simulate this eclipse
at a distance of 21 centuries?
If we knew the time of an event in UTC or TDB
(tdb),
we could go there with
Celestia:settime
(settime).
But Celx has no built-in way to
find
the time of an event.
How could we compute the time of a full Moon,
or a sunset,
or a perihelion of Mercury?
The following program displays the date and time of the full moon of January, 2014. First it creates a local function f that accepts a TDB time. The function returns a continuously increasing value that is negative before the full moon, zero at the instant of fullness, and positive afterwards. A continuously decreasing function would have worked just as well.
We assume that there is exactly one full moon between the times
a
and
b.
The program passes
f,
a,
and
b
to the standard library function
std.zerostd.zero.
This function tries to find a
zerozero of function
or
rootroot of function
of
f
in the range
[a, b],
i.e., a number
t
such that
a ≤ t ≤ b
and
f(t) = 0.
If
std.zero
finds that
f(a)
or
f(b)
is zero,
we have our root and no further work is necessary.
Otherwise,
std.zero
goes into the following loop,
performing an unsophisticated
bisection
algorithmbisection algorithm.
If
f(a)
and
f(b)
are of the same sign (both positive or both negative),
std.zero
reports an error.
Otherwise,
f(a)
and
f(b)
are of opposite signs
and there is a root between
a
and
b
because
f
is continuous.
std.zero
takes a stab at finding this root by computing the value of f
at the midpoint
c
between
a
and
b.
If
f(c)
is zero,
we have our root.
Otherwise, depending on whether
f(c)
is positive or negative,
std.zero
uses the half interval to the left or right of
c
as the new interval and repeats the loop.
--[[
Display the date and time of the full moon of January, 2014.
Look at it from the sublunar point on the Earth, with the ecliptic horizontal.
]]
require("std")
--variables used by f:
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local moon = celestia:find("Sol/Earth/Moon")
local lockFrame = celestia:newframe("lock", earth, sol)
--[[
f is the function that will be passed to std.zero. It returns the longitude in
radians of the Moon in the lockFrame's XY plane, minus pi radians. The return
value is negative before the full moon, zero at the full moon, and positive
thereafter. f will be called by std.zero, probably many times.
The lockFrame's XY plane is the plane of the ecliptic. The X axis points from
the Earth towards the Sun. The negative X axis points from the Earth away from
the Sun. The Moon is new when it's on the X axis, and full when it's on the
negative X axis.
We want to measure the following position's longitude in the lockFrame's XY
plane. But Position:getlonglat returns a longitude in the XZ plane. We
therefore have to create a new position. Warning: the Z axis points "down" in
the XZ plane, but the Y axis points "up" in the lockFrame's XY plane. That's
why we have to negate the y coordinate.
]]
local function f(t)
assert(type(t) == "number")
local position = lockFrame:to(moon:getposition(t), t)
position = celestia:newposition(
position:getx(),
position:getz(),
-position:gety())
--The Moon is full when it's on the negative X axis.
--The longitude of this axis is math.pi.
return position:getlonglat().longitude - math.pi
end
local function main()
local observer = celestia:sane()
celestia:hidelabel("moons") --We know that the Moon is the Moon.
celestia:select(moon)
--Find the full moon between times a and b.
local a = celestia:utctotdb(2014, 1, 9)
local b = celestia:utctotdb(2014, 1, 23)
local t = std.zero(f, a, b)
--celestia:settimescale(0) --if you want to freeze the full moon
celestia:settime(t)
observer:setframe(lockFrame)
local kilometers = earth:radius() + earth:getinfo().atmosphereHeight
local microlightyears = kilometers / KM_PER_MICROLY
local position = celestia:newposition(-microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
observer:lookat(moon:getposition(), std.yaxis)
local kilometers = moon:getposition():distanceto(observer:getposition())
assert(kilometers > 0)
local angularRadius = math.asin(moon:radius() / kilometers)
observer:setfov(3 * angularRadius) --Let Moon be 2/3 height of window.
local utc = celestia:tdbtoutc(t)
local s = string.format(
"Full moon\n"
.. "%.17g\n"
.. "%s %d, %d\n"
.. "%02d:%02d:%.15g UTC",
t,
std.monthName[utc.month], utc.day, utc.year,
utc.hour, utc.minute, utc.seconds)
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
Full moon
2456673.7043342134
January 16, 2014
04:53:8.29164505004883 UTC
Each iteration of the loop in
std.zero
halves the interval of uncertainty,
thus doubling the precision of the answer
and appending one more correct binary bit to its mantissa.
Since the mantissa has only
std.mantissastd.mantissa
bits (probably 53 on your machine; see
doubleArithmetic),
there is never any reason for
std.zero
to iterate more than this number of times.
We can control how many times
it loops by passing it an optional fourth argument,
a table containing one or more of the following fields.
The loop halts when any of the conditions are satisfied.
A missing fourth argument defaults to
the table
{maxiter = std.mantissa}.
How well does the output of this program agree with the lunar phase websites of NASANASA Sky Calendar and the U. S. Naval ObservatoryUnited States Naval Observatory?
http://eclipse.gsfc.nasa.gov/SKYCAL/SKYCAL.html
http://aa.usno.navy.mil/data/docs/MoonPhase.php
The above program found a full moon at TDB time t = 2456673.7043342134. Does the function f really increase strictly around t? Is our answer really the best?
Let’s evaluate
f
at the three numeric values adjacent to t in both directions.
Pass three arguments to
std.zero.
Append a newline
\n
to the end of the existing
format.
Insert the following loop immediately before the call to
Celestia:print.
std.consecutive(t, 3) do
s = s .. string.format("% d %-18.17g % .15g\n", i, t1, f(t1))
end
-3 2456673.704334212 -1.79859238613744e-10
-2 2456673.7043342125 -8.99302854406869e-11
-1 2456673.7043342129 -3.25206528373201e-12
0 2456673.7043342134 8.50852721612227e-11
1 2456673.7043342139 1.73429715033535e-10
2 2456673.7043342143 2.6167645827968e-10
3 2456673.7043342148 3.51550788479926e-10
To use this program we must first have a pair of times, a and b, that delimit the search interval. The two numbers can’t be too far apart, since the function f exhibits its steadily increasing behavior only for the 29-day interval centered at a full moon.
Suppose we were not given an a and b for January, 2014, and we had to find them ourselves. Write a loop that finds the angular distance between the Sun and Moon as seen from the Earth on several days throughout the month. Then estimate the time of the full moon and pick an a and b on either side of it. Could there be more than one full moon in a calendar month?
We can make our function f much simpler:
--Return positive before the full moon, zero at the full moon, and negative --afterwards. local function f(t) assert(type(t) == "number") return lockFrame:to(moon:getposition(t), t):gety() endThe original f allowed us to use an a and b that were up to half a synodic month (solarDays) away from the full moon. How close together do the a and b have to be for this simpler f?
Read the function
std.zero
in the standard library file
std.lua
in
stdCelx.
Our naïve
std.zero
always picks a
c
halfway between
a
and
b.
But consider a case where
f(a) = –1
and
f(b) = 9.
Since zero is only
10%
of the way from
f(a)
to
f(b),
it would make sense to pick a
c
that is only
10%
of the way from
a
to
b.
In other words,
c = a +
b − a
f(b) − f(a)
This is called the
regula falsi
algorithmregula falsi algorithm.
Will it converge with fewer iterations?
--[[
Print the date and time in 2025 when Saturn's rings are edge-on as seen from
Earth. Show an Earth's-eye view from the sub-Saturn point.
]]
require("std")
--variables used by f:
local earth = celestia:find("Sol/Earth")
local saturn = celestia:find("Sol/Saturn")
--XZ plane is the plane of the rings.
local equatorialFrame = celestia:newframe("equatorial", saturn)
--Return value is negative when Earth is south of the ring plane,
--positive when it is north.
local function f(t)
assert(type(t) == "number")
local position = equatorialFrame:to(earth:getposition(t), t)
return position:getlonglat().latitude
end
local function main()
local observer = celestia:sane()
local a = celestia:utctotdb(2025) --defaults to January 1
local b = celestia:utctotdb(2026)
local t = std.zero(f, a, b)
celestia:settime(t)
local lockFrame = celestia:newframe("lock", earth, saturn)
observer:setframe(lockFrame)
local kilometers = earth:radius() + earth:getinfo().atmosphereHeight
local microlightyears = kilometers / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
--rings horizontal
observer:lookat(saturn:getposition(), equatorialFrame:from(std.yaxis))
--Zoom in to make Saturn half the hight of the window (if it wasn't
--so oblate).
kilometers = earth:getposition():distanceto(saturn:getposition())
local angularRadius = math.asin(saturn:radius() / kilometers)
observer:setfov(4 * angularRadius)
local utc = celestia:tdbtoutc(t)
local s = string.format(
"%s's rings edge-on:\n"
.. "%s %d, %d\n"
.. "%02d:%02d:%02d UTC",
saturn:name(), std.monthName[utc.month], utc.day, utc.year,
utc.hour, utc.minute, std.round(utc.seconds))
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
Saturn's rings edge-on:
March 23, 2025
18:07:24 UTC
--[[
Print the date and time of the start of the current year's spring in the Earth's
northern hemisphere. Show a Sun's-eye view of the Earth's axis lying broadside
to the Sun, with the Earth's orbit horizontal.
]]
require("std")
--variables used by f:
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local equatorialFrame = celestia:newframe("equatorial", earth)
--[[
Return the Sun's longitude in the equatorial frame XZ plane.
The equatorial frame X axis points toward's the Earth's current vernal equinox.
The longitude is negative before the equinox, positive thereafter.
]]
local function f(t)
assert(type(t) == "number")
local position = equatorialFrame:to(sol:getposition(t), t)
local longitude = position:getlonglat().longitude
--A longitude of 359 degrees is treated as -1 degree.
if longitude > math.pi then
longitude = longitude - 2 * math.pi
end
return longitude
end
local function main()
local observer = celestia:sane()
earth:addreferencemark({type = "planetographic grid"})
earth:addreferencemark({type = "spin vector"}) --Earth's axis
local lockFrame = celestia:newframe("lock", earth, sol)
observer:setframe(lockFrame)
--Spring starts around March 21.
local year = celestia:tdbtoutc(celestia:gettime()).year
local guess = celestia:utctotdb(year, 3, 21)
local a = guess - 2
local b = guess + 2
local t = std.zero(f, a, b)
celestia:settime(t)
local microlightyears = (5 * earth:radius()) / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
observer:lookat(lockFrame:from(std.position0),
lockFrame:from(std.zaxis))
local utc = celestia:tdbtoutc(t)
local s = string.format(
"Start of spring in Earth's northern hemisphere:\n"
.. "%s %d, %d\n"
.. "%02d:%02d:%.15g UTC",
std.monthName[utc.month], utc.day, utc.year,
utc.hour, utc.minute, utc.seconds)
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
Start of spring in Earth's northern hemisphere:
March 20, 2014
16:52:23.7786296010017 UTC
Run the above program. The press ** (rear-view mirror command) (asterisk, the rear-view mirror command) to see the Sun at the vernal equinox in Pisces.
When is the first day of summer in the northern hemisphere of Earth? When is the first day of summer in the northern hemisphere of Mars?
Let’s position the observer with a bodyfixed frame in New York City, ten meters above sea level to avoid the worst of the jittersjitter (of planetary surface). Then we’ll compute the altitude and azimuth of the center of the Sun with an altazimuth frame. The light of the setting Sun is bent 35′ downwards (35 minutes of arc, 35/60 degrees) by atmospheric refractionrefraction of light, so some part of the Sun remains visible until its upper limb (edge) sinks to 35′ below the horizon. That event marks the official time of sunset.
--[[
Print the time of today's sunset in New York City. Look at it too.
]]
require("std")
--variables used by f:
--New York City.
--zone is approximately -5, because New York is 5 hours behind Greenwich.
local latitude = math.rad( 40 + (39 + 51 / 60) / 60 ) --north positive
local longitude = math.rad(-(73 + (56 + 19 / 60) / 60)) --west negative
local zone = math.deg(longitude) * 24 / 360
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
local observerPosition = celestia:newpositionlonglat(
longitude + 2 * math.pi, --plus 2pi to make it nonnegative
latitude,
(earth:radius() + .01) / KM_PER_MICROLY
)
local rotation = celestia:newrotationaltaz(longitude, latitude)
local altazFrame = celestia:newframe("bodyfixed", earth, rotation)
--[[
Return the angular distance in radians above or below the horizon of the upper
limb of the Sun, plus 35 minutes of arc for atmospheric diffraction.
angularRadius is the Sun's angular radius in radians as seen by the observer.
altitude is the angular distance in radians above or below the horizon of the
Sun's center.
]]
local function f(t)
assert(type(t) == "number")
local solPosition = sol:getposition(t)
local observerPosition = bodyfixedFrame:from(observerPosition, t)
local distance = observerPosition:distanceto(solPosition)
assert(distance > 0)
local angularRadius = math.asin(sol:radius() / distance)
local toSol = solPosition - observerPosition
toSol = altazFrame:to(toSol, t)
local altitude = toSol:getlonglat().latitude
return altitude + angularRadius + math.rad(35 / 60)
end
local function main()
local observer = celestia:sane()
observer:setframe(bodyfixedFrame)
observer:setposition(bodyfixedFrame:from(observerPosition))
--Sun usually sets around 6:00 p.m.
local utc = celestia:tdbtoutc(celestia:gettime())
local guess = celestia:utctotdb(utc.year, utc.month, utc.day, 18 - zone)
local a = guess - 3 / 24
local b = guess + 3 / 24
local t = std.zero(f, a, b)
--or five minutes earlier to catch the last rays: t - 5 / (60 * 24)
--Celestia does not know about refraction.
celestia:settime(t)
--Horizon horizontal, zenith overhead. Must come after settime.
observer:lookat(sol:getposition(), altazFrame:from(std.yaxis))
local utc = celestia:tdbtoutc(t)
local lat = std.tolat(latitude)
local long = std.tolong(longitude)
local ns = {[1] = "N", [0] = "", [-1] = "S"}
local ew = {[1] = "E", [0] = "", [-1] = "W"}
local s = string.format(
"Sunset\n"
.. "Latitude %d%s %d%s %.15g%s %s\n"
.. "Longitude %d%s %d%s %.15g%s %s\n"
.. "%s %d, %d\n"
.. "%02d:%02d:%.15g UTC",
lat.degrees, std.char.degree,
lat.minutes, std.char.minute,
lat.seconds, std.char.second,
ns[lat.signum],
long.degrees, std.char.degree,
long.minutes, std.char.minute,
long.seconds, std.char.second,
ew[long.signum],
std.monthName[utc.month], utc.day, utc.year,
utc.hour, utc.minute, utc.seconds)
celestia:print(s, 60, -1, 1, 1, -1)
wait()
end
main()
Sunset
Latitude 40° 39′ 50.9999999999997″ N
Longitude 73° 56′ 19.0000000000134″ W
February 26, 2013
22:44:6.24706953763962 UTC
The above observer gazes horizontally at the setting Sun,
causing the blank surface of the Earth to fill the lower half of the window.
The user would probably rather see more of the sky.
Pitch the observer upwards to lower his horizon.
Change the call to
Observer:lookat
to the following.
The TitanicTitanic sank during the night of April 14–15, 1912 at latitude 41° 43′ 55″ North, longitude 49° 56′ 45″ West. Nautical twilightnautical twilight is the period when the center of the Sun is 12° to 6° below the horizon. Simulate the sky as seen at the start of nautical twilight by the CarpathiaCarpathia as she arrived early on the 15th to rescue the survivors.
What is the date of the earliest sunset in the current year at your location? Why isn’t it the date of the winter solstice? See the equation of timeequation of time in Analemma.
Does the
perihelion
of
Mercury’s
orbit really
precess
around the Sun
as
EinsteinEinstein, Albert
predicted?
To find out,
we would first have to compute the time of a perihelion.
But unlike our previous examples,
which dealt with a function
f
that was steadily increasing
or decreasing,
this problem
deals with a distance that reaches a minimum and then starts to increase.
Does this mean that we can’t use our
std.zerostd.zero.
The Mercury chase frame and the Mercury/Sol lock frame
coöperate to provide the solution.
The XY plane of both frames is the plane of Mercury’s orbit.
The negative X axis of the chase frame
points in the direction of Mercury’s motion.
The positive X axis of the lock frame points towards the Sun.
At perihelion, these axis are perpendicular to each other.
Before perihelion, the angle between them is less than 90°.
After perihelion, the angle is greater than 90°.
We now have a steadily increasing
f
that we can feed to
std.zero
--[[
Find the date and time of Mercury’s first perihelion during the current
calendar year. Show an overhead view looking down on the plane of the
orbit, with the Sun at the center of the window and Mercury to the right.
]]
require("std")
local sol = celestia:find("Sol")
local mercury = celestia:find("Sol/Mercury")
local chaseFrame = celestia:newframe("chase", mercury)
local lockFrame = celestia:newframe("lock", mercury, sol)
--How much greater than pi/2 radians is the angle between the chase frame
--negative X axis and the lock frame X axis?
local function f(t)
assert(type(t) == "number")
local forward = chaseFrame:from(-std.xaxis, t)
local toSol = lockFrame:from(std.xaxis, t)
return forward:angle(toSol) - math.pi / 2
end
local function main()
local observer = celestia:sane()
celestia:show("orbits") --When Mercury is selected, show its orbit.
celestia:select(mercury)
--Show no other orbits.
celestia:setorbitflagsCelestia:setorbitflags({Planet = false, Moon = false})
--Estimate the first perihelion of the current calendar year.
local orbitPeriod = mercury:getinfo().orbitPeriod
local utc = celestia:tdbtoutc(celestia:gettime())
local start = celestia:utctotdb(utc.year, 1, 1)
local finish = start + orbitPeriod
local minKilometers =
mercury:getposition(start):distanceto(sol:getposition(start))
local minTime = start
for t = start + 1, finish do
local kilometers =
mercury:getposition(t):distanceto(sol:getposition(t))
if kilometers < minKilometers then
minKilometers = kilometers
minTime = t
end
end
local guess = minTime
local a = guess - 2
local b = guess + 2
local t = std.zero(f, a, b)
celestia:settime(t)
local solmercuryFrame = celestia:newframe("lock", sol, mercury)
observer:setframe(solmercuryFrame)
local microlightyears =
5 * (mercury:getposition() - sol:getposition()):length()
local position = celestia:newposition(0, 0, microlightyears)
observer:setposition(solmercuryFrame:from(position))
observer:lookat(sol:getposition(), solmercuryFrame:from(std.yaxis))
local utc = celestia:tdbtoutc(t)
local s = string.format(
"Mercury perihelion\n"
.. "%s %d, %d\n"
.. "%02d:%02d:%.15g UTC\n"
.. "%.15g kilometers",
std.monthName[utc.month], utc.day, utc.year,
utc.hour, utc.minute, utc.seconds,
sol:getposition():distanceto(mercury:getposition()))
celestia:print(s, 60, -1, 1, 1, -6)
wait()
end
main()
Mercury perihelion
February 3, 2014
23:31:54.3350332975388 UTC
46001057.7836216 kilometers
To verify that we found the perihelion, print the Sol-Mercury distance 10 minutes before the perihelion, at the perihelion, and 10 minutes after.
local kilometers = sol:getposition(t):distanceto(mercury:getposition(t))Can we reduce the intervals to five minutes or less?
Does the vector in the universal frame from Sol to Mercury at perihelion
precess
around the Sun?
Remove the existing string
s
and
insert the following code immediately after the
settime.
I get a precession of about 560″ or 580″ per century, depending on the choice of the perihelion at the start of the century. Classical mechanics predicts a precession down in the low 530’s.
Find the time of the periapsis before the epoch for NereidNereid (moon of Neptune)’s orbit around Neptune in recoverElliptical. Then find Nereid’s position at this time. Compute two more of Nereid’s orbital elements: the mean anomalymean anomaly (orbital element) at the epoch, and the argument of the pericenterargument of pericenter (orbital element).
To find a function’s maximum or minimum, as opposed to its root, try the golden section searchgolden section search.
The above a is the semi-major axis of the orbit, T is the period, and e is the eccentricity. If we take the speed of light c in kilometers per second, then a must be in kilometers and T must be in seconds. The angle ε is in radians. The eccentricity e is a dimensionless ratio.
--Speed of light in kilometers per second. Can also use std.cstd.c.
local c = KM_PER_MICROLY * 1e6 / (60 * 60 * 24 * 365.25)
--Mercury's period in seconds
local T = mercury:getinfo().orbitPeriod * 24 * 60 * 60
--Values for Mercury taken from data/solarsys.ssc comments.
local a = 0.3871 * std.kmPerAu --semi-major exis in kilometers
local e = 0.2056 --eccentricity
--orbitsPerCentury from previous exercise
local precessionPerOrbit =
24 * math.pi^3 * a^2 / (T^2 * c^2 * (1 - e^2))
local precessionPerCentury = precessionPerOrbit * orbitsPerCentury
local s = string.format("Precession per century: %.15g%s",
60 * 60 * math.deg(precessionPerCentury), std.char.second)
Precession per century: 43.0052916346402″
Mercury is at its greatest elongationelongation (of Mercury) east when it is at the greatest angular distance east of the Sun as seen from the Earth. At this time, Mercury stays above the horizon after sunset for the longest interval.
Find the time of Mercury’s next greatest elongation east. At the moment of greatest elongation, the Mercury-to-Sol and Mercury-to-Earth vectors are perpendicular. Before that time, the vectors are separated by more than 90°; afterwards, by less than 90°.
As I schoolboy I learned that Mercury keeps the same face towards the Sun. Let’s see where this “fact” came from. Mercury’s surface features can be seen from Earth most clearly when Mercury is at its greatest elongation from the Sun. Find the time interval between these events, using the formula in solarDays for the time it takes Mercury to cycle through its phases. How long does it take for Mercury to rotate with respect to the universal frame? And with respect to the Earth? Does Mercury present the same face to the Earth at each time of greatest elongation east?
The position and orientation of the observer
can be updated with each tick of the Celestia simulation.
We did this with the tick handler
in tickHandler
and the
tick
Lua hook in
luaHookFunctions.
Similarly, the
position and orientation of a celestial object
can be updated with each tick.
We will do this with the
scripted orbit
in
Geostationary
and the
scripted rotation
in
scriptedRotation.
Let’s invent a celestial object named Particle in
geostationary orbit
around the Earth.
We created the file
data/imaginary.ssc
containing the Particle in
objectGetposition.
Make it visible by giving it a
RadiusRadius (in .ssc file)
and
ColorColor (in .ssc file),
and also give it a
ScriptedOrbitScriptedOrbit (in .ssc file)
containing the attributes
ModuleModule (of ScriptedOrbit)
and
FunctionFunction (of ScriptedOrbit).
#This file is data/imaginary.ssc.
#List it in celestia.cfg under SolarSystemCatalogs after "data/solarsys.ssc".
"Particle" "Sol/Earth"
{
Radius 1000 #in kilometers
Color [1 .5 0] #red, green, blue
#The name of the file is particleorbit.lua.
#The name of the function in that file is geostationary.
ScriptedOrbit {
Module "particleorbit"
Function "geostationary"
}
}
Place the following file
particleorbit.lua
in the Celx directory
(celxDirectory).
We would prefer to name it
particleorbit.celx
since it contains Celx code,
but see
standard.
The file contains a
geostationary
function which creates and returns a table
that acts like an
objectobject (in programming language)
in an object-oriented language,
complete with fields and methods.
For a similar “object”,
see the Lua hook table in
luaHookFunctions.
The table returned by the function must contain a
boundingRadiusboundingRadius (of scripted orbit)
field in kilometers.
This tells Celestia that it doesn’t have to worry about drawing the
orbit of the Particle at any point more than the given distance
from the Particle’s primary.
The table must also contain a
periodperiod (of scripted orbit)
field to indicate that the orbit is
periodicperiodic scripted orbit:
it repeats itself.
Celestia will draw the entire orbit only if it is periodic,
because a nonperiodic orbit would rapidly turn into spaghetti.
The table must also contain a
positionposition (of scripted orbit)
method returning the
x,
y,
z
coördinates of the Particle at a given TDB time,
in the equatorial frame of the primary.
The coördinates are always kilometers even if the object is a comet.
Note that they are returned in a non-standard order,
with the
z
negated.
The same order is used in
Phase:getposition.
Our
position
method
will keep the particle in geostationary orbit above
0°
N
0°
E,
in the South Atlantic.
We would normally use the name
position
for the
bodyfixedPosition
field,
but a table cannot have two fields with the same name.
The standard library cannot be
requirerequire (Lua function)d
when the
particleorbit.lua
file is executed.
It has to be required later, when the
position
method is first called.
We had the same problem with the the Lua hook table;
see
standard.
Error messages from the
position
method may appear in the Celestia console
(console).
Or they might disappear entirely and
Celestia:find
will report that the
Particle
is missing.
Do not call the
waitwait
function
(wait)
in the
position
method:
the
wait
will never return.
--[[
This file is particleorbit.lua.
Put the celestial object (the Particle) in geostationary orbit around the Earth
at 0 degrees N 0 degrees E over the South Atlantic.
]]
function geostationary(parameters) --must be a nonlocal function
--This table of parameters will be used in an exercise.
assert(type(parameters) == "table")
return {
--Three fields that I invented.
--They have no special meaning to Celestia.
bodyfixedFrame = nil,
equatorialFrame = nil,
bodyfixedPosition = nil,
--Three fields that do have a special meaning to Celestia.
--The third field is a method.
boundingRadius = 50000, --in kilometers
period = 1, --in Earth days
position = function(self, tdb)
assert(type(self) == "table" and type(tdb) == "number")
if package.loaded.std == nil then --std not required yet
require("std")
local earth = celestia:find("Sol/Earth")
self.equatorialFrame =
celestia:newframe("equatorial", earth)
self.bodyfixedFrame =
celestia:newframe("bodyfixed", earth)
--radius of circular geostationary orbit
local microlightyears = 42164 / KM_PER_MICROLY
self.bodyfixedPosition =
celestia:newposition(microlightyears, 0,
0)
end
--The object's position must be returned
--in the equatorial frame.
local p = self.bodyfixedPosition
p = self.bodyfixedFrame:from(p, tdb)
p = self.equatorialFrame:to(p, tdb)
--The object's position must be returned in kilometers,
--not microlightyears.
p = KM_PER_MICROLY * p
local x = p:getx()
local y = p:gety()
local z = p:getz()
return x, -z, y --Celestia expects non-standard order.
end
}
end
--[[
This is the regular Celx file containing the main function.
Look down on the Earth from above the north pole, letting us see the entire
geostationary orbit over the equator. Earth's equatorial X axis points right
(the meridian of 0h right ascension is to the right), Z axis down, and Y axis
towards the user.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:show("orbits") --When the Particle is selected, show its orbit.
--Show no other orbit.
celestia:setorbitflagsCelestia:setorbitflags({Planet = false, Moon = false})
local earth = celestia:find("Sol/Earth")
earth:addreferencemark({type = "body axes"}) --X axis points to Particle
local particle = celestia:find("Sol/Earth/Particle")
celestia:select(particle)
local equatorialFrame = celestia:newframe("equatorial", earth)
observer:setframe(equatorialFrame)
--[[
How far would the observer have to be from the Earth in order to fit the
whole orbit into the user's window, with a 1-degree margin at top and
bottom?
]]
local angularRadius = observer:getfov() / 2 - math.rad(1)
local linearRadius = 42164 --height in kilometers of geostationary orbit
local kilometers = linearRadius / math.tanmath.tan(angularRadius)
local microlightyears = kilometers / KM_PER_MICROLY
local position = celestia:newposition(0, microlightyears, 0)
observer:setposition(equatorialFrame:from(position))
--Look down at the Earth's north pole.
--Equatorial frame X axis points right, Z towards bottom of window,
--Y towards observer.
observer:lookat(earth:getposition(), equatorialFrame:from(-std.zaxis))
--one day of simulation time per minute of real time
celestia:settimescale(60 * 24)
wait()
end
main()
If the optional
period
field is present,
the entire orbit will be drawn.
If
period
is absent,
only the part of the orbit delimited by the
beginDatebeginDate (of scripted orbit)
and
endDateendDate (of scripted orbit)
will be drawn.
Let’s draw half of the 24-hour orbit.
The dates have to be hardcoded in, since
Celestia:gettimeCelestia:gettime
cannot be called at the early time when the table is created.
(On the Macintosh executable from the Celestia download page,
no orbitbug in Celestia
is drawn with
beginDate
and
endDate
and the Celestia console
[console]
says “GL Error: 1281”.
But if you compile Celestia from its source code on Mac
[compileMacintosh],
it will work correctly.)
Instead of hardcoding values such as 2013 and 42164 into the
geostationary
function,
we can pass them in as parameters from
data/imaginary.ssc.
The values can be numbers, strings, or booleans
(true
or
false).
The following
geostationary
function moves the Particle along the orbit we just saw in
Geostationary.
We can run it with the same Celx program,
the same
data/imaginary.ssc,
and the same
celestia.cfg.
But this version of the function
implements the geostationary orbit with totally different machinery.
It simulates the force of gravity on the Particle,
and the Particle’s resulting acceleration.
The vector
toPrimary
points from the Particle to the Earth;
the Earth will pull the Particle along this line.
The magnitude of the gravitational force obeys an
inverse-square
lawinverse-square law:
F =
GMm
r2
where
GG (gravitational constant)
is the
gravitational
constantgravitational constant (G)
6.672 · 10–11
N · m2/kg2,
M
and
m
are the masses of the Earth and the Particle in kilograms,
and
r
(for “radius”)
is the distance from the Earth to the Particle in meters.
The magnitude also obeys the second most famous equation in all of physics,
Newton’s
F = ma
which brings in the acceleration.
Putting the equations together,
we have
ma =
F =
GMm
r2
We cancel the
m
on both sides to get the magnitude of the Particle’s acceleration
caused by the
Earth’s gravity,
in meters per second per second.
a =
GM
r2
Now consider the time interval between two consecutive calls to
position.
The Particle already has a velocity given by the vector
self.velocity.
We have just computed the magnitude of the
acceleration
vector,
pointing from the Particle towards the Earth.
To compute the Particle’s new velocity after a one-second interval,
we simply add
acceleration
to
self.velocity.
If the interval was two seconds long,
we would have added
2 * acceleration.
And now that we have the Particle’s velocity,
we can compute its new position.
The Particle already has a position given by
self.pos.
To compute the Particle’s new position after a one-second interval,
we simply add
self.velocity
to
self.pos.
If the interval was two seconds long,
we would have added
2 * self.velocity.
The
gravitational constant
G
is in the standard library as
std.Gstd.G,
with a value taken from
version/src/celengine/astro.cpp.
It is defined in terms of meters.
The field
self.G
is the same constant,
but defined in terms of microlightyears.
The
mass of the EarthEarth, mass of,
self.M,
is also taken from
astro.cpp.
The eccentricityeccentricity (orbital element) e of the Particle’s orbit is given by
e = rv2 GM – 1We saw in tailPoints that an orbit of eccentricity 0 is a circle. Solving the above equation for v when e = 0, we get
v = GM/r
--[[
This file is particleorbit.lua.
Put the celestial object (the Particle) in geostationary orbit around the Earth
at latitude 0 degrees N longitude 0 degrees E over the South Atlantic.
]]
function geostationary(parameters)
assert(type(parameters) == "table")
return {
boundingRadius = 50000, --kilometers
--The Particle is not rendered when the period is present;
--see exercise below.
--period = 1,
G = nil, --gravitational constant
M = 5.976e24, --mass of Earth in kilograms, i.e. 5.976 * 10^24
pos = nil,
velocity = nil,
lastTdb = nil,
position = function(self, tdb)
if package.loaded.std == nil then --std not required yet
require("std")
self.G = std.G / (1000 * KM_PER_MICROLY)^3
local earth = celestia:find("Sol/Earth")
local equatorialFrame =
celestia:newframe("equatorial", earth)
local bodyfixedFrame =
celestia:newframe("bodyfixed", earth)
--height of geostationary orbit, in microly
local r = 42164 / KM_PER_MICROLY
self.pos = celestia:newposition(r, 0, 0)
self.pos = bodyfixedFrame:from(self.pos, tdb)
self.pos = equatorialFrame:to(self.pos, tdb)
--speed of circular orbit,
--in microlightyears per second.
local speed = math.sqrt(self.G * self.M / r)
--Z is negative because the initial position is
--at "3 o'clock" in the XZ plane and the
--Particle is orbiting counterclockwise.
self.velocity = celestia:newvector(0, 0, -speed)
self.velocity =
bodyfixedFrame:from(self.velocity, tdb)
self.velocity =
equatorialFrame:to(self.velocity, tdb)
else
--vector from Particle to its primary
local toPrimary = std.position0 - self.pos
local r = toPrimary:length() --microlightyears
assert(r > 0)
toPrimary = toPrimary:normalize()
--seconds since last call to this method
local seconds =
(tdb - self.lastTdb) * 60 * 60 * 24
local acceleration =
(self.G * self.M / r^2) * toPrimary
self.velocity =
self.velocity + seconds * acceleration
self.pos = self.pos + seconds * self.velocity
end
self.lastTdb = tdb
local p = KM_PER_MICROLY * self.pos
local x = p:getx()
local y = p:gety()
local z = p:getz()
return x, -z, y
end
}
end
The above
r
is the radius in microlightyears of the circular geostationary orbit.
Let’s
compute this value instead of hardwiring it in.
As always,
velocity is distance divided by time:
v =
2πr
T
The (italic)
r
in this equation is the radius of the orbit in meters,
and
2πr
is the circumference in meters.
T
is the orbital period in seconds,
and
v
is the velocity in meters per second.
Second, a particle’s
centripetal
accelerationcentripetal acceleration
(acceleration towards the primary) in a circular orbit is
a =
v2
r
Combined with our earlier formula for
a,
we have
GM
r2
=
a
=
v2
r
=
4π2r
T2
Solving for
r3
yields
r3
=
GMT2
4π2
and then we take cube roots on both sides.
--radius of circular geostationary orbit
--local r = 42164 / KM_PER_MICROLY
local earth = celestia:find("Sol/Earth")
local T = earth:getinfo().rotationPeriod
* 24 * 60 * 60
local radicand =
std.G * self.M * (T / (2 * math.pi))^2
local r = math.pow(radicand, 1/3)
local s = string.format("r = %.15g meters\n", r)
r = r / 1000
s = s .. string.format("r = %.15g kilometers\n",
r)
r = r / KM_PER_MICROLY
s = s .. string.format(
"r = %.15g microlightyears", r)
celestia:print(s, 60)
The above orbit of eccentricity e = 0 is a circle. An orbit of eccentricity 0 < e < 1 would be an ellipse. An orbit with e = 1 is a parabola. Verify that if we solve the eccentricity equation for v when e = 1, we get
v = 2GM/rDemonstrate by experimentation that this speed is the escape velocity at distance r from the center of the Earth. At this speed, the Particle will move along a parabola to infinity.
Our
“impulse power”
position
function assumes that the
tdb
argument increases slightly with each call.
The argument behaves this way because we commented out the
period
field of the table returned by
geostationary.
To comment the field back in,
the
position
function would have to be robust enough to accept arguments in a random order.
Do this by having the first call to
position
build up a table of times and positions.
The strength of gravity falls off with the square of the distance. So does the strength of light. Before the age of computers, the Swedish astronomer Erik HolmbergHolmerg, Erik modeled the gravitational interaction between galaxiesgalaxies, gravitational interaction between by placing light bulbs on a table, 37 bulbs for each galaxy. He measured the intensity of the incoming light at each bulb, moved the bulbs accordingly, and repeated the process.
Make a group of galaxies and watch them interact. Start with a pair of galaxies and simulate the two-body problemtwo-body problem. Do the galaxies deform each other as they get close?
Place a satellite in low Earth orbit and introduce air resistanceair resistance.
Send a spacecraft on a Hohmann transfer orbitHohmann transfer orbit from a low circular orbit to a higher one.
Launch a projectile straight up from
Tampa, Florida
(latitude
27°
7′
North,
longitude
5°
7′
West,
measured from the meridian of Washington, DC).
Give it an initial velocity of
12,000
yards per second.
(A yard is 36 inches;
convert to millimeters with
std.mmPerInstd.mmPerIn.)
Is this less than escape velocity?
If so,
how long does it take the projectile to reach maximum altitude?
Pick a time and place for the launch that will get the projectile
as close to the Moon as possible when the Moon is at
perigee.
What happens?
With a tick handler, the analemmaanalemma program in Analemma laboriously kept the observer aimed at the meridian of the mean Sunmean Sun. Everything would be easier if we had a planet identical to the Earth, except that it rotated once per year at a constant speed. The observer could then simply adhere to the bodyfixed frame of this planet.
Let’s temporarily give the Earth a scripted rotation that rotates once per year, keeping the existing axis and direction of rotation.
#Excerpt from the entry for the Earth in data/solarsys.ssc. #Replace the existing CustomRotation with the following. ScriptedRotationScriptedRotation (in .ssc file)
{
ModuleModule (of ScriptedRotation) "earthrotation" #filename will be earthrotation.lua
FunctionFunction (of ScriptedRotation) "oncePerYear" #function name will be oncePerYear
}
The following function
oncePerYear
returns a table containing a method named
orientation,
which returns the
w,
x,
y,
z
components of the orientation the Earth should have at time
tdb.
There’s one caveat;
let’s illustrate it with the simplest example of an orientation.
local orientation = celestia:newrotation(std.xaxis, 0) --a.k.a. std.orientation0std.orientation0
assert(orientation.w == 1) --w is the real part
assert(orientation.x == 0) --(x, y, z) is the imaginary part
assert(orientation.y == 0)
assert(orientation.z == 0)
If the function returned the above orientation,
the Earth’s bodyfixed Y axis would point towards
the north pole of the ecliptic in
Draco,
its X axis would point towards the autumnal equinox in
Virgo,
and its Z axis towards the summer solstice in
Taurus/Gemini.
Note that this is not the orientation we would naïvely expect.
We would think that a return value of
std.orientation0
would orient the Earth so that the Earth’s bodyfixed axes
would be point in the same direction as those of the universal frame.
Instead,
the Earth has been twirled
180°
around the universal Y axis.
To correct the situation,
the function should untwirl the Earth with another rotation of
180°
around the Y axis.
For other examples of this rotation, see
alternativeBodyfixed
and
Phase:getorientation.
Now let’s look at the
orientation
method below.
The function
math.fmodmath.fmod
divides
tdb
by
self.orbitPeriod
and returns the remainder
t.
After making it nonnegative,
t
is in the range
0 ≤ t < self.orbitPeriod
The fraction
t / self.orbitPeriod
is therefore in the range
0 ≤
t
self.orbitPeriod
< 1
which causes
theta
(the amount of rotation around the Earth’s axis) to be in the range
0 ≤ theta < 2π
This rotation is combined with the
23°
rotation
self.toPolaris
that moves the Earth’s north pole from
Draco
to
Polaris.
--[[
This file is earthrotation.lua.
Rotate the Earth once per orbitPeriod at a constant rate.
]]
function oncePerYear(parameters) --must be a nonlocal function
assert(type(parameters) == "table")
return {
orbitPeriod = nil,
untwirl = nil,
toPolaris = nil,
orientation = function(self, tdb)
assert(type(self) == "table" and type(tdb) == "number")
if package.loaded.std == nil then --std not required yet
require("std")
self.orbitPeriod = celestia:find("Sol/Earth")
:getinfo().orbitPeriod
--Make return value agree with universal frame.
self.untwirl = celestia:newrotation(std.yaxis,
math.pi)
--Tilt the Earth so that its axis points to
--Polaris, not to Draco.
self.toPolaris = celestia:newrotation(std.xaxis,
std.tilt)
end
local t = math.fmod(tdb, self.orbitPeriod)
if t < 0 then
t = t + self.orbitPeriod --Make t nonnegative.
end
local theta = 2 * math.pi * t / self.orbitPeriod
--one rotation per orbit period
local orient = self.untwirl
* celestia:newrotation(-std.yaxis, theta)
* self.toPolaris
--Return the 4 components of the orientation.
local w = orient.w
local x = orient.x
local y = orient.y
local z = orient.z
return w, x, y, z
end
}
end
Compare the following
main
function with the more complicated program in
Analemma.
--[[
Move the Sun along the analemma.
Station the observer on the Earth's equator at the subsolar meridian.
Look straight up at the celestial equator, with Polaris towards top of window.
]]
require("std")
local function main()
local observer = celestia:sane()
local year = celestia:tdbtoutc(celestia:gettime()).year --current year
celestia:settime(celestia:utctotdb(year, 6, 13)) --equation of time is 0
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
local lockFrame = celestia:newframe("lock", earth, sol)
--two vectors in bodyfixedFrame
local toPolaris = std.yaxis
local toSol = bodyfixedFrame:to(lockFrame:from(std.xaxis))
toSol = toPolaris:erect(toSol)
local kilometers = earth:radius() + earth:getinfo().atmosphereHeight
local microlightyears = kilometers / KM_PER_MICROLY
local position = microlightyears * toSol:toposition()
observer:setposition(bodyfixedFrame:from(position))
observer:lookat(
bodyfixedFrame:from(2 * position), --away from center of Earth
bodyfixedFrame:from(std.yaxis))
--Tall enough to see top and bottom of analemma, plus 1-degree margin.
--Celestial equator horizontal in the middle.
observer:setfov(2 * (std.tilt + math.rad(2)))
--Ten days of simulation time per second of real time.
celestia:settimescale(60 * 60 * 24 * 10)
celestia:mmprint()
wait()
end
main()
Should we have interfered with the Earth’s rotation in
data/solarsys.ssc?
Or would it have been cleaner to create an invisible new planet
("Sol/Earth2")
with a scripted orbit that follows the Earth,
and a scripted rotation that rotates once per year?
What effect would this have on
Object:family?
We can change the position and/or orientation of an observer in four ways.
To move him in a straight line at a constant speed
(with Newton’s
“rectilinear
motionrectilinear motion”),
call the method
Observer:setspeedObserver:setspeed.
To move him in a straight line
with a pre-programmed acceleration and deceleration,
call
Observer:goto
(animateRotation).
To move him along a circular arc, call
Observer:centerorbit.
And to move him along an arbitrary curve at arbitrary speeds,
write a tick handler function
(tickHandler)
or a
tick Lua hook
(luaHookFunctions)
that sets his position and/or orientation by calling
Observer:setposition,
setorientation,
and/or
lookat
with each tick of the simulation.
If we don’t care how the observer gets to his destination,
it’s easiest to call
goto.
If we need to know
the observer’s position at any time along the way,
or his time at any position,
it’s easiest to program the journey ourselves by writing a tick handler
or
tick
hook.
But even so,
we might still prefer a
goto
to give our program the standard Celestia look and feel that comes from the
gotoObserver:goto’s
celebrated
“exponential acceleration”.
This section shows how to compute his position at any time during a
goto.
“Is such ignorance possible?” gasped someone.
“Maybe I exaggerate. Let’s say x e to the x.”
Where will the Celestia observer be at any given time while executing a
gotoObserver:goto
(animateRotation)?
And at what time will he pass a given point in space?
The answers depend on the subtle interplay between his position, speed, and
acceleration.
Let’s review our Calculus with a simpler problem,
and then return to the
goto.
How far will a car go if it travels at 60 miles per hour for two hours? Obviously, all we have to do is multiply 60 times 2. The following diagram is a picture of the multiplication. The hight is the speed, the width is the elapsed time, and the area is equal to the distance traveled. Thus we have taken a problem about finding a distance, and turned it into an equivalent problem about finding an area.
The driver’s position, speed, and acceleration are given by the following functions. The t is the elapsed time in hours since the start of the journey. The position is the driver’s distance in miles from the origin. The acceleration is zero because the speed is constant (except for the jackrabbit start and the precipitous halt). The phrase “per hour per hour” is abbreviated “per hour2”.
| position | = | 60t | miles |
| speed | = | 60 | miles per hour |
| acceleration | = | 0 | miles per hour per hour |
The expression 60 is the derivativederivative of 60t, i.e., the speed of an object that is at position 60t at time t. Conversely, 60t is an antiderivativeantiderivative of 60, i.e., the position at time t of an object moving at a speed of 60. The same terminology is used to talk about the relationship between speed and acceleration. The expression 0 is the derivative of 60, and 60 is an antiderivative of 0.
Given the speed of 60, we can compute the area in the above diagram and thus the total distance traveled. The speed is written after the integral sign ∫ in the following equation. Its antiderivative 60t is written before the vertical bar. We evaluate the antiderivative at the ending and starting times t = 2 and t = 0. (For example, the value of the antiderivative 60t at time t = 2 is 120.) Then we subtract the values and get the area.
area of rectangle = 2
Now let’s return to the observer and his
goto.
The
main
function in the following program positions him along the positive X axis
of the universal frame, 1 kilometer from the origin.
The
goto
moves him away from the origin along the X axis
with exponential speed and acceleration.
During the first half of the duration of the journey,
his position, speed, and acceleration
are given by the following functions.
The
t
is the elapsed real time in seconds since the start of the
goto.
The constant
ee (mathematical constant)
is
expexp (transcendental function)(1)
≈
2.71828182845905,
the base of the
natural
logarithmnatural logarithm.
The position is his distance in kilometers from the origin,
i.e., his
x
coördinate.
The function
et
has the miraculous property of being its own derivative
and its own antiderivative,
causing this example’s position, speed, and acceleration
to be the same.
| position | = | et | kilometers |
| speed | = | et | kilometers per second |
| acceleration | = | et | kilometers per second per second |
At time
t = 0
the observer’s position is
e0 = 1
kilometer from the origin
and his universal frame coördinates in microlightyears are
(1/KM_PER_MICROLY, 0, 0).
At time
t = 1
his position is
e1 = e
kilometers from the origin and his coördinates are
(e/KM_PER_MICROLY, 0, 0).
During the second half of the journey,
his speed is a mirror image of the first half.
As before, the hight in the diagram is the speed,
the width is the elapsed time,
and the area is equal to the distance traveled.
The duration of the
goto
will be two seconds of real time,
causing each half of the journey to take one second.
Given the above speed,
we can compute the distance in kilometers
traveled during the acceleration phase, from
t = 0
to
t = 1.
The total distance (from t = 0 to t = 2) will be twice as great.
The following
accelTime
is the fraction of the first half of the duration spent in acceleration.
The same fraction of the second half is spent in deceleration.
With our
accelTime
of 1,
the entire first half is spent in acceleration
and the entire second half in deceleration.
No time is left in the middle for cruising at the maximum speed.
The function
math.expmath.exp
computes
et.
For example,
math.exp(0)
is
e0 = 1
and
math.exp(1)
is
e1 = e.
The
“exp factor”
f
will be used later.
For the time being it is 1 and makes no difference at all.
The duration of a
goto
is measured in seconds of real time.
And with our default timescale of 1
(settime),
the real time and the simulation time should pass at the same rate.
But the simulation time returned by
Celestia:gettimeCelestia:gettime
is smoother than the
“frothy”
real time returned by
Celestia:getscripttimeCelestia:getscripttime.
For additional precision,
we set the time to a small value with
Celestia:settimeCelestia:settime.
A larger value would have more digits to the left of the decimal point,
permitting fewer digits to the right.
--[[
Move the observer away from the origin along the universal X axis for two
seconds with a goto.
During the first half of the duration of the goto,
his distance from the origin at time t seconds is exp(t) kilometers
and his distance from the starting point is exp(t) - exp(0) kilometers.
His speed and acceleration during the second half are the mirror images
of his speed and acceleration during the first half.
Therefore during the second half, his distance from the ending point
at time 2-t seconds is exp(t) - exp(0) kilometers.
His ending point is exp(0) + 2 * (exp(1) - exp(0)) = 1 + 2 * (e - 1) kilometers
(approximately 4.43656365691809 kilometers) from the origin.
Compute his position with every tick during the goto, and display the maximum
error in kilometers in his computed position.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
celestia:settime(0) --bigger times would get rounded more
local t0 = celestia:gettime() --time of start of goto
local halfDuration = 1 --half of duration of goto, in real-time seconds
local totalDuration = 2 * halfDuration
--distance traveled, in kilometers, during each half of the duration
local halfDistance = math.exp(halfDuration) - math.exp(0)
local totalDistance = 2 * halfDistance
--This "exp factor" will be needed later.
--For now, it is equal to 1 and can be ignored.
local f = math.log(halfDistance + 1) / halfDuration
--starting position's distance from origin, in kilometers
local startingX = math.exp(f * 0)
local maxError = 0 --kilometers
local parameters = {
accelTime = 1, --accelerate for the entire first half of the duration
duration = totalDuration,
--As always, position objects are in microlightyears.
from = celestia:newposition(startingX / KM_PER_MICROLY, 0, 0),
to = celestia:newposition(
(startingX + totalDistance) / KM_PER_MICROLY, 0, 0)
}
local function tickHandler()
if observer:travellingObserver:travelling() then
--seconds since start of goto
local t = (celestia:gettime() - t0) * 60 * 60 * 24
--true if we're in the second half of the goto
local secondHalf = t > halfDuration
--t1 is t's distance from the start time or the end time,
--whichever is closer.
local t1 = t
if secondHalf then
t1 = totalDuration - t
end
--x is the observer's actual x coordinate in kilometers
local x = observer:getposition():getx() * KM_PER_MICROLY
--x1 is the observer's computed x coordinate in kilometers
local distance = math.exp(f * t1) - math.exp(f * t0)
if secondHalf then
--Second half is mirror image of first half.
distance = totalDistance - distance
end
local x1 = startingX + distance
local error = math.absmath.abs(x - x1)
if error > maxError then
maxError = error
end
local s = string.format("max error: %.15g kilometers", maxError)
celestia:print(s, 60)
end
end
local function main()
celestia:registereventhandler("tick", tickHandler)
observer:setposition(parameters.from) --one kilometer from origin
observer:goto(parameters)
wait()
end
main()
The maximum error is about 200 nanometersnanometer.
max error: 2.04703365369596e-10 kilometers
During the first half of the duration of the
goto,
the observer travels
e − 1
kilometers.
When will he be 1 kilometer from his starting point?
Solving
s
∫
0
et dt
=
et
|
|
|
|
|
s
0
=
es − e0
=
es − 1
=
1
for s
seconds,
we get a
natural
logarithm:
s = lnln (transcendental function) 2 ≈ .6931471805599453
Can you use the tick handler to verify that at
t = ln 2,
his distance is 1 kilometer from the starting point
and 2 kilometers from the origin?
The rather baroque
halfDistance
in the above program was chosen to get us the simplest possible
exponential function,
et,
for the observer’s position and speed
during the first half of the duration.
If we want the
goto
to have an arbitrary
halfDistance
of
d
kilometers,
the position and speed functions will require an
“exp factor”
f
with a value different from 1.
| position | = | eft | kilometers |
| speed | = | feft | kilometers per second |
Let’t find the value of this
f.
It must satisfy the following equation,
because the integral is the distance covered during the acceleration phase.
1
∫
0
feft dt
=
d
An antiderivative of
feft
is
eft,
so the value of the integral is
1
∫
0
feft dt
=
eft
|
|
|
|
|
1
0
=
ef
–
e0
=
ef
– 1
Solving
ef
– 1
=
d
for f,
we get
In our original
goto,
the carefully engineered
halfDistance
of
e − 1
kilometers allowed the exp factor
f
to be a simple 1.
Now try a
goto
that covers a
totalDistance
of
1,000
kilometers.
Observer that
f
is no longer 1.
The
halfDuration
in the above program was chosen to get us the simplest possible
exponential function,
et,
for the observer’s position and speed
during the first half of the duration.
If we want the
goto
to take an arbitrary
halfDuration
of
b
seconds to cover a
halfDistance
of
d
kilometers,
the exp factor
will have to satisfy the following equation.
Solving for f, we get
f = ln (d + 1) b
In our original
goto,
the carefully engineered
halfDuration
of 1 second allowed the exp factor
f
to be a simple 1.
Now try a
goto
that takes a
totalDuration
of 10 seconds to cover a
totalDistance
of 1000 kilometers.
Let’s give the
goto
an
accelTime
of .5,
meaning that
the first
50%
of the first half of the duration
will be spent in acceleration,
and the last
50%
of the last half of the duration
in deceleration.
In other words,
the first
25%
of the total duration will be spent in acceleration
and the last
25%
in deceleration.
The middle
50%
of the total duration will be spent
in cruising at a constant speed.
Let’s take a total duration of 4 seconds.
In the following equation,
the
accelTime
a
is .5,
the
halfDuration
b
is 2 seconds,
and
ab
is the number of seconds spent in the acceleration phase.
With our values of a and b,
ab is 1.
The integral is the distance in kilometers
covered during the acceleration phase,
ending at a speed of
eab
kilometers per second
at time
t = ab
seconds.
This
eab
is the constant speed during the cruising phase.
The
(1 − a)b
is the number of seconds spent in the first half of the cruising phase.
The product
(1 − a)beab
is the distance in kilometers covered during the
first half of the cruising phase.
We will solve for the
halfDistance
d
in kilometers.
Since this example’s exp factor f is 1,
we do not bother to write it.
The value of the integral is
ab
The
halfDistance
d
is therefore
The
halfDistance
in the above exercise was chosen to give us the value of 1 for the
exp factor
f.
If we give the
goto
an arbitrary
halfDistance
of
d
kilometers,
f
will have to satisfy the following equation.
The value of the integral is
abstd.zero
(fullMoon).
With the values shown below,
f
will be approximately
0.212653869582051.
Read the functions in Celestia that calculate the exp factor
f.
The member function
TravelExpFunc::operator()
in
version/src/celengine/observer.cpp
is like our function
findF,
except that it refers to the exp factor as x,
the product
a * b
as
s,
and
the
halfDistance
as
dist.
The template function
solve_bisection
in
version/src/celmath/solve.h
is like our function
std.zero.
Once the exp factor has been chosen,
the member function
Observer::update
in
version/src/celengine/observer.cpp
computes the observer’s position.
The method
Observer:goto
moves the observer in a straight line.
The method
Observer:centerorbitObserver:centerorbit
moves him in a circular arc.
Let’s use it to orbit with
Apollo
8Apollo 8.
Launch was at 12:51 UTC on December 21, 1968 and the iconic Earthrise came 75h 47m later. The spacecraft was then in its fourth revolution around the Moon, cruising in an almost circular orbit 113 kilometers above the lunar surface. Although it had orbited the Earth from west to east (counterclockwise when viewed from above the north pole), Apollo 8 orbited the Moon from east to west. The astronauts therefore saw the Earth rising in the west.
The observer in the following program rides with the spacecraft.
The Moon occupies the lower portion of the scene,
not reaching as high as the center of the window;
the Earth is initially hidden by the Moon.
The call to
centerorbit
orbits the observer around the Moon
until the Earth rises into view and becomes is centered in the window.
This causes the Moon to rotate below him,
but it always occupies the same region of the window.
The observer orbits around an axis that goes through the center of the Moon.
The Moon is not mentioned explicitly in the call to
centerorbit
because this method automatically uses the reference object of the frame
to which the observer has been
setframeObserver:setframed.
The frame must not be the universal frame,
which has no reference object.
Frame:getcoordinatesystem() == "universal" then
celestia:print("Observer:centerorbit would do nothing.", 10)
else
local reference = frame:getrefobjectFrame:getrefobject()
celestia:print("Observer:centerorbit will orbit him around "
.. reference:name() .. ".", 10)
end
The axis around which the observer orbits, and the angle through which he orbits around the axis, are determined by his initial position and orientation. The orbit continues until the observer is (approximately) facing the Earth. More precisely, the orbit continues until his forward vector becomes parallel to the vector from his original position towards the Earth. The following two vectors give us a simple way to state precisely what happens.
The axis of the orbit is the cross product of the above vectors; the angle of the orbit is the angle between the vectors. For another example of this providential arrangement, see crossRotation. While the orbit is in progress, the center of the Moon remains at a fixed point in the observer’s field of view.
One complication:
Celestia:newvectorlonglatCelestia:newvectorlonglat
measures the longitude in the XZ plane,
but the lock frame measures it in the XY plane.
And we have to negate the z coördinate because
the Z axis points “down” in the XZ plane,
while the Y axis points “up” in the XY plane.
--[[
Simulate the Apollo 8 Earthrise with Observer:centerorbit.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:settime(celestia:utctotdb(1968, 12, 21, 12, 51, 0.0) --launch
+ (75 + 47 / 60) / 24) --T plus 75h 47m
celestia:setambientCelestia:setambient(0) --Moon too bright with the default of .1
celestia:hide("constellations", "ecliptic", "grid", "nightmaps")
--For photorealism, turn off all the labels.
local flags = celestia:getlabelflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setlabelflags(flags)
local earth = celestia:find("Sol/Earth")
local moon = celestia:find("Sol/Earth/Moon")
local lockFrame = celestia:newframe("lock", moon, earth)
observer:setframe(lockFrame)
local kilometers = 113 + moon:getinfo().radius
local microlightyears = kilometers / KM_PER_MICROLY
--Degrees east of sub-Earth point on the Moon.
--Far enough east so that Earth is initially below the lunar horizon.
--Spacecraft is orbiting east to west.
local theta = math.rad(90 + 22)
local position =
celestia:newpositionlonglat(theta, 0, microlightyears)
position = celestia:newposition(
position:getx(), -position:getz(), position:gety())
position = lockFrame:from(position)
observer:setposition(position)
--Get the observer's lunar longitude and latitude.
local bodyfixedFrame = celestia:newframe("bodyfixed", moon)
local longlat = bodyfixedFrame:to(position):getlonglat()
local altazFrame = celestia:newframe("bodyfixed", moon,
celestia:newrotationaltaz(longlat.longitude, longlat.latitude))
--Earth rises in the west (azimuth 270).
local forward = celestia:newvectoraltaz(math.rad(-17), math.rad(270))
local up = celestia:newvectoraltaz(math.rad(90), math.rad(0))
local orientation = celestia:newrotationforwardup(forward, up)
observer:setorientation(altazFrame:from(orientation))
observer:setverticalfov(math.rad(15)) --zoom in a bit
assert(observer:getframe():getcoordinatesystem() ~= "universal")
observer:centerorbit(earth, 30) --30 seconds, unhurried
wait()
end
main()
Through how many degrees of arc does the above program
orbit the observer?
Assuming that a lunar orbit takes two hours,
how many seconds should the
centerorbit
take?
Better yet,
use the formula for the velocity of a circular orbit in
Impulse.
Our
centerorbit
came close to centering the Earth in the window
because the Earth is far away and the Moon is small.
Would
centerorbit
center a nearby object when orbiting the observer around a large object?
Is there any way we could trick
centerorbit
into dividing by zero?
Read the implementation of
Observer:centerorbit.
It calls the C++ function
Observer_centerorbit
in
version/src/celestia/celx_observer.cpp,
which calls the member function
Observer::centerSelectionCO
(“Center Orbit”)
in
version/src/celengine/observer.cpp,
which calls the member function
Observer::computeCenterCOParameters
in the same file.
What does
centerorbit
do to the observer’s up vector?
Suppose we wanted to do a lot of lunar orbiting.
Would it be easier to set the observer’s position and orientation with a
tick handler
(tickHandler)
or a
tick Lua hook
(luaHookFunctions)
instead of with
centerorbit?
Observer:orbit:
an Instantaneous JumpThe following program places the Earth in front of the observer in the most straightforward orientation. He is above latitude 0° North longitude 0° East in the South Atlantic, with the Earth centered in the window and the north pole up.
Then
Observer:orbit
instantly orbits him around an axis that goes through the center of
the Earth.
The call does not have to mention the Earth,
because this method implicitly uses the reference object of the frame to
which the observer has been
setframed.
The axis of the orbit is specified as
std.xaxis.
But this is not the X axis of the universal frame
or the frame to which the observer has been
setframed.
It is the X axis of his
personal frameobserver’s personal frame
(overviewFrames),
which always points to his current right.
Thus the axis of the orbit is the vector
that goes through the center of the Earth,
and that is parallel to the vector that points to the observer’s
current right.
The rotation slides him up the
Prime Meridian
to the
Tropic
of CancerTropic of Cancer
in the western
Sahara.
The center of the Earth stays directly in front of him
because
Observer:orbit
changes his orientation as well as his position.
The north pole stays towards the top of the window.
--[[
Demonstrate Observer:orbit. Rotate the observer around an axis that goes
through the center of the Earth and that is parallel to the observer's X axis,
which always points to his current right.
]]
require("std")
local function main()
local observer = celestia:sane()
local earth = celestia:find("Earth")
earth:addreferencemark({type = "body axes"})
earth:addreferencemark({type = "planetographic grid"})
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
--Position the observer at 0 degrees N, 0 degrees E.
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local position = celestia:newpositionlonglat(
math.rad(0),
math.rad(0),
microlightyears)
observer:setposition(bodyfixedFrame:from(position))
--Face the center of the Earth, with the north pole up.
observer:lookat(
bodyfixedFrame:from(std.position0), --or earth:getposition()
bodyfixedFrame:from(std.yaxis))
wait(5)
--Now position him at 23 degrees N, 0 degrees E.
--He will still be facing the center of the Earth, with north pole up.
local rotation = celestia:newrotation(std.xaxis, std.tilt)
observer:orbit(rotation)
wait()
end
main()
The next example lets the user tick his or her way around the planetographic grid of the Earth with the four arrow keys. Each keystroke jumps him to the next point where a visible line of latitude and a visible line of longitude cross. (In geocaching circles, these points are known as confluencesconfluence.)
Read the code for the up and down arrows first
because these cases are the most simple.
The lines they follow are meridians of longitude,
which, being great circles,
are easy to
orbit
the observer along.
Then read the code for the left and right arrows.
The lines they follow are parallels of latitude,
which, because they are usually not great circles,
are harder to
orbit
along.
To construct the axis
of the orbit,
we start by letting the variable
axis
be the axis of the Earth
in the coördinates of the universal frame.
Then we
transformRotation:transform
this axis
into the coördinates of the observer’s personal frame,
and
orbit
him around it.
How exactly do we perform the transformation?
The simplest example
would be an observer in the initial orientation:
the
std.orientation0std.orientation0
in
orientation,
facing
Taurus/Gemini
with
Draco
overhead.
In this case,
the axes of the observer’s personal frame
are parallel to those of the universal frame,
and no transformation is necessary.
And indeed the code would perform no transformation on the axis,
since the
conjugateconjugate of rotation
of
std.orientation0
is the very same
std.orientation0,
which is a rotation of zero degrees.
Another simple example would be an observer in this orientation:
--Face Orion, with Polaris overhead.
local orientation = celestia:newrotation(std.xaxis, std.tilt)
He has pitched
23°
down from the initial orientation,
so everything he sees has pitched
23°
up.
This explains the call to
conjugateRotation:conjugate
in the following program.
And indeed the resulting
Rotation:transform
would pitch the
axis
23°
up.
We have to call the
keydown
Lua hook
(luaHookFunctions)
because the four
arrow keys
are not recognized by
celestia_keyboard_callback
(callback)
or the key handler
(keyHandler).
--[[
This file is luahook.celx.
When the user presses the four arrow keys, orbit the observer one step around
the Earth along the lines of latitude and longitude. The Earth remains centered
in the window. In fact, a vertical line of longitude and a horizontal line of
latitude always cross at the center of the window. (When the observer is above
a pole, the horizontal line of latitude degenerates to a point.)
]]
celestia:setluahook {
observer = nil,
earth = nil,
bodyfixedFrame = nil,
--At 5 Earth radii from the center of the Earth,
--the planetographic grid lines are 10 degrees apart.
tickSize = math.rad(10),
keydownkeydown (Lua hook) = function(self, key, modifiers)
assert(type(key) == "number" and type(modifiers) == "number")
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
self.observer = celestia:getobserver()
self.earth = celestia:find("Sol/Earth")
self.bodyfixedFrame =
celestia:newframe("bodyfixed", self.earth)
end
--Do nothing until the main function has selected the Earth.
--Objects can't be compared, but their names can.
if celestia:getselectionCelestia:getselection():name() ~= self.earth:name() then
return false
end
--Left arrow, go left. Left is initially west, but it will
--become east if the observer crosses a pole.
if key == 1 then
--axis of Earth,
--in coordinates of universal frame
local axis = self.bodyfixedFrame:from(std.yaxis)
--axis of Earth,
--in coordinates of observer's frame
axis = self.observer:getorientation()
:conjugate():transform(axis)
local rotation = celestia:newrotation(axis,
self.tickSize)
self.observer:orbit(rotation)
return true
end
--Right arrow, go right. Right is initially east.
if key == 2 then
local axis = self.bodyfixedFrame:from(std.yaxis)
axis = self.observer:getorientation()
:conjugate():transform(axis)
local rotation = celestia:newrotation(-axis,
self.tickSize)
self.observer:orbit(rotation)
return true
end
--Up arrow, go up. Up is initially north.
if key == 3 then
local rotation = celestia:newrotation(
std.xaxis, self.tickSize)
self.observer:orbit(rotation)
return true
end
--Down arrow, go down. Down is initially south.
if key == 4 then
local rotation = celestia:newrotation(
-std.xaxis, self.tickSize)
self.observer:orbit(rotation)
return true
end
return false
end
}
--[[
This main function goes with the above luahook. Position the
observer above latitude 0 degrees N, longitude 0 degrees E on Earth, with the
Earth centered in the window and the north pole up.
]]
require("std")
local function main()
local observer = celestia:sane()
local earth = celestia:find("Earth")
earth:addreferencemark({type = "body axes"})
earth:addreferencemark({type = "planetographic grid"})
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
--Position the observer at 0 degrees N, 0 degrees E.
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local position = celestia:newpositionlonglat(
math.rad(0),
math.rad(0),
microlightyears)
observer:setposition(bodyfixedFrame:from(position))
--Face the center of the Earth, with the north pole up.
observer:lookat(
bodyfixedFrame:from(std.position0),
bodyfixedFrame:from(std.yaxis))
celestia:print("Press the 4 arrow keys to tick around the Earth.", 10)
celestia:select(earth) --Hook does nothing until this select.
wait()
end
main()
Have the above hook print the observer’s latitude and longitude.
Here’s another way to create the
rotation
for the left and right arrows,
eliminating the
conjugate.
Give the Lua hook table a
self.latitude
field containing the observer’s number of ticks
north or south of the equator.
Initialize it to zero,
and update it when the user presses an up or down arrow.
Let’s assume the observer is above a point in the Earth’s northern
hemisphere, so
self.latitude
is positive.
When the left arrow is pressed,
we rotate him
theta
radians down to the equator.
Then we rotate him
self.tickSize
radians west along the equator.
Finally, we rotate him back up to his original latitude.
All of this is done with a single
rotation
built as the
productquaternion multiplication
of the three rotations shown below.
Read them from right to left.
Each of the three component rotations moves the observer along a great circle,
but their product does not.
The planetographic grid lines are
10°
apart when the diameter of the planet
is at least 200 pixels,
and
30°
apart when the planet is smaller.
(See the C++ member function
PlanetographicGrid::render
in
version/src/celengine/planetgrid.cpp
for the implementation.)
After reading
fieldOfView,
compute the radius of the Earth in pixels and update the
self.tickSize
accordingly.
Would it be simpler to do all the
Observer:orbit
examples with a tick handler
(tickHandler)
that calls
Observer:setposition
and
Observer:setorientation?
The problems in this section straddle the divide between simulation space and real space. For example, we might need to set the width and height of the Celestia window to save it as an image file. What will this do to the horizontal and vertical fields of view, or to the radius in pixels of a planet in the window? If a nearsighted user leaned close to the window, or a farsighted user leaned away, how should we adjust the fields of view to avoid distortion as the apparent size of the window changed? And what would this do to the magnification?
A Celx program has no ability to resize the Celestia window. It has to be resized manually, by dragging on the lower right corner. But the program can provide continuous feedback to the user as the drag is in progress.
The following program displays the current dimensions of the window. Resize the window manually as you run it. When the desired dimensions are reached, interrupt the program with the escape key or quit Celestia. When you run the next Celx program, the window will retain have the dimensions that you set.
Celestia:getscreendimensionCelestia:getscreendimension
returns the dimensions in pixels of the Celestia window,
not of the computer screen.
They do not include the scroll bars or title bar.
The values are integers.
The default fields of view are the angles that would be subtended by the window
from the point of view of a user 400 millimeters away.
This distance is set by the
int
data member
CelestiaCore::distanceToScreen
in
version/src/celestia/celestiacore.cpp
and the
const
int
REF_DISTANCE_TO_SCREEN
in
version/src/celengine/render.cpp.
A user closer than 400 millimeters would have a wider field of view,
and vice versa.
--[[
Display the current window dimensions.
Drag on the lower right corner of the window to resize it.
Pres comma and period to increase and decrease the field of view.
]]
require("std")
--[[
Return the greatest common divisor of two nonnegative integers.
For example, gcd(30, 42) == 6.
More realistically, given the typical window size, gcd(1024, 768) == 256.
This is a
recursiverecursion function: it calls itself.
]]
local function gcd(a, b)
--a and b must be integersinteger, check for.
assert(type(a) == "number" and math.absmath.abs(a) == math.floormath.floor(a))
assert(type(b) == "number" and math.abs(b) == math.floor(b))
if b == 0 then
return a
end
--Now that we know that b is nonzero, it's safe to divide by b.
--The %% (remainder operator) is the Lua remainder (or modulus) operator.
return gcd(b, a % b)
end
--variables used by tickHandler:
local observer = celestia:sane()
local fontName = celestia:getparamstring("TitleFont")
assert(fontName ~= "") --TitleFont parameter missing from celestia.cfg
local font = celestia:loadfont("fonts/" .. fontName)
local charWidth = font:getwidth("M")
assert(charWidth > 0)
local charHeight = font:getheight()
local function tickHandler()
local windowWidth, windowHeight = celestia:getscreendimension()
local divisor = gcd(windowWidth, windowHeight)
assert(divisor > 0)
local vFov = observer:getverticalfov()
local hFov = observer:gethorizontalfov()
local lines = windowHeight / (charHeight + 1) --1 pixel between lines
local characters = windowWidth / charWidth
local lineNumbers = ""
for i = 9, lines - 1 do
lineNumbers = lineNumbers .. string.format(" %2d\n", i)
end
if lines >= 9 then
lineNumbers = lineNumbers .. ("M"):repstring.rep(characters)
end
local s = string.format(
" 1 Window dimensions: %d %s %d pixels\n"
.. " 2 Aspect ratio: %d : %d\n"
.. " 3 Vertical field of view: %g%s\n"
.. " 4 Horizontal field of view: %g%s\n"
.. " 5 Default vertical field of view: %g%s\n"
.. " 6 Default horizontal field of view: %g%s\n"
.. " 7 Window holds %g lines, each %d pixels high, in %s.\n"
.. " 8 A line consists of %g ems, each %d pixels wide.\n"
.. "%s",
windowWidth, std.char.times, windowHeight,
windowWidth / divisor, windowHeight / divisor,
math.deg(vFov), std.char.degree,
math.deg(hFov), std.char.degree,
math.deg(std.getverticalfov()), std.char.degree,
math.deg(std.gethorizontalfov()), std.char.degree,
lines, charHeight, fontName,
characters, charWidth,
lineNumbers)
celestia:print(s, math.huge, -1, 1, 0, -1)
end
local function main()
--Keep the Sun in view, but get away from its glare.
observer:setposition(std.position)
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
1 Window dimensions: 1024 × 768 pixels
2 Aspect ratio: 4 : 3
3 Vertical field of view: 28.5035°
4 Horizontal field of view: 37.4191°
5 Default vertical field of view: 28.5035°
6 Default horizontal field of view: 37.4191°
7 Window holds 30.72 lines, each 24 pixels high, in sansbold20.txf.
8 A line consists of 64 ems, each 16 pixels wide.
9
etc.
29
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
Is the default vertical field of view in the above program correct?
Assume the window size is 1024 × 768 pixels.
One inch equals 96 pixels
(std.pixelsPerInstd.pixelsPerInch)
or 25.4 millimeters
(std.mmPerInstd.mmPerIn).
The default vertical field of view should be exactly twice the following angle
θ.
Is the value for the default horizontal field of view correct?
Create the first argument of the above
string.formatstring.format
with Lua
long bracketslong brackets (Lua syntax).
A
newlinenewline (character)
immediately after the opening
[[[[ ]] (long brackets)
is ignored.
Let the format be a named variable. Count the newlines in it by removing every character that is not a newline.
local format = [[ 1 Window dimensions: %d %s %d pixels 2 Aspect ratio: %d : %d 3 Vertical field of view: %g%s 4 Horizontal field of view: %g%s 5 Default vertical field of view: %g%s 6 Default horizontal field of view: %g%s 7 Window holds %g lines, each %d pixels high, in %s. 8 A line consists of %g ems, each %d pixels wide. %s]] local n = format:gsubstring.gsub("[^\n]", ""):lenstring.len() --n is 8
The vertical and horizontal fields of view can be
“set”
and
“get”
with the following methods of class
Observer.
Their arguments and return values are in radians
(radians).
Since the Celestia window is usually in
landscape orientationlandscape orientation
(wider than it is tall),
the vertical field is usually more constraining,
and therefore more heavily used,
than the horizontal field.
That’s why the vertical methods have shorter synonyms.
| vertical fov | horizontal fov | |
|---|---|---|
| set |
setverticalfovObserver:setverticalfov
setfovObserver:setfov
|
sethorizontalfovObserver:sethorizontalfov
|
| get |
getverticalfovObserver:getverticalfov
getfovObserver:getfov
|
gethorizontalfovobserver:gethorizontalfov
|
Let’s see how
Observer:gethorizontalfov
computes the horizontal field of view
from the window dimensions and the vertical field.
We’ll take a window of size 1024 × 768 pixels
and a vertical field of
32°.
Since the aspect ratio is
4:3,
we would naïvely expect the horizontal field of view would be
4
3
32°
≈
42.6666666666667°
But as we’re about to see,
this turns out to be an overestimation.
The window subtends an angle of 32° vertically, so the upper half of the window subtends 16°.
To see that angle of
16°,
the user would have to be
384
tantangent (trig function) 16°
≈
1339.16714643491
pixels from the window.
At 96 pixels per inch
(std.pixelsPerInstd.pixelsPerIn)
and 25.4 millimeters per inch
(std.mmPerInstd.mmPerIn),
this works out to approximately
354 millimeters,
significantly less than the user’s default distance of 400 millimeters.
And now that we know the user’s distance from the window, we can compute the horizontal field of view.
2 arctan 512 384 / (tan 16°) ≈ 41.8464280764382°
Let’s use the field of view methods to display an image of the
Moon
whose radius is exactly 100 pixels,
centered in the window.
The following observer is positioned
at the top of the Earth’s atmosphere above the
sublunar
pointsublunar point
on the Earth—the point where the Moon is directly overhead.
This point lies on the X axis of the Earth-Moon lock frame.
Given this position,
what is the vertical field of view that would yield
a lunar image of radius 100 pixels?
We begin by computing the
angularRadius
in radians subtended by half of the moon as seen by the observer.
angularRadius
=
arcsinarcsine (trig function)
radius
distance
The same angle should be spanned by the 100 pixels in the window. (Note: the above diagram is in simulation space [realSpace]. The following diagram is in real space.)
To get that angle,
the user would have to be
100
tan angularRadius
pixels from the center of the lunar image on the window.
Given this distance,
the angle spanned by the upper or lower half of the window
from the user’s point of view is
arctan
height of window / 2
100 / (tan angularRadius)
The total vertical field of view will be twice as large.
--[[
Look at the Moon from the sublunar point on Earth, with the Moon's orbit
horizontal. Set the vertical field of view to get an apparent lunar radius of
100 pixels.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "galaxies", "grid")
celestia:settimescaleCelestia:settimescale(0) --so we can capture the image at our leisure
--For photorealism, turn off all labels and overlays.
local flags = celestia:getlabelflags()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setlabelflags(flags)
flags = celestia:getoverlayelements()
for key, value in pairs(flags) do
flags[key] = false
end
celestia:setoverlayelements(flags)
local earth = celestia:find("Sol/Earth")
local moon = celestia:find("Sol/Earth/Moon")
local lockFrame = celestia:newframe("lock", earth, moon)
observer:setframe(lockFrame)
--the sublunar point on the Earth
local kilometers = earth:radius() + earth:getinfo().atmosphereHeight
local microlightyears = kilometers / KM_PER_MICROLY
local position = celestia:newposition(microlightyears, 0, 0)
observer:setposition(lockFrame:from(position))
observer:lookat(moon:getposition(), lockFrame:from(std.zaxis))
--distance and radius() in kilometers, angularRadius in radians
local distance =
observer:getposition():distanceto(moon:getposition())
assert(distance > 0)
local angularRadius = math.asinmath.asin(moon:radius() / distance) --of Moon
local width, height = celestia:getscreendimensionCelestia:getscreendimension()
local pixels = 100 --desired radius of lunar image, in pixels
local tangent = math.tanmath.tan(angularRadius)
assert(tangent > 0)
local verticalFov = 2 * math.atan2math.atan2(height / 2, pixels / tangent)
observer:setverticalfov(verticalFov)
local s = string.format(
"Window dimensions: %d %s %d pixels\n"
.. "Fields of view: %f%s %s %f%s\n"
.. "Lunar radius: %d pixels, %f%s\n"
.. "Ambient light: %f",
width, std.char.times, height,
math.deg(observer:gethorizontalfov()), std.char.degree,
std.char.times,
math.deg(observer:getverticalfov()), std.char.degree,
pixels, math.deg(angularRadius), std.char.degree,
celestia:getambientCelestia:getambient())
celestia:print(s, math.huge, -1, -1, 1, 5)
wait()
end
main()
The fields of view and the angular diameter of the Moon will vary slightly, depending on whether the Moon is at apogee or perigee.
Window dimensions: 1024 × 768 Fields of view: 2.778766° × 2.084253° Lunar radius: 100 pixels, 0.271415° Ambient light: 0.100000
Let’s save the Celestia window in an image file on the disk.
Add the following code to the Moon program in
fieldOfView
immediately after the call to
Celestia:print.
The first argument of
Celestia:takescreenshotCelestia:takescreenshot
can be either
"jpg"
or
"png".
The second argument specifies part of the name of the image file to be created.
This part can be at most 16 characters
and is restricted to letters, digits, and underscores.
The
boolean
return value must be converted
tostringtostring (Lua function)
before it can be formatted with
%s,
because the current version of Celestia does not have Lua 5.2.
On platforms other than Macintosh,
the above code creates an image file named
screenshot-moon-000001.png.
Warning:
if
takescreenshot
is called a second time in the same program,
or if the same instance of Celestia runs any other Celx program with
takescreenshot,
it creates another file named
screenshot-moon-000002.png.
But if Celestia is restarted and runs any Celx program with
takescreenshot,
it creates a new file named
screenshot-moon-000001.png
that overwrites the original file.
If the
ScriptScreenshotDirectory
is set to the empty string
""
in
celestia.cfg,
the image file is placed in the Celx directory.
When specifying the
ScriptScreenshotDirectory
in Microsoft Windows,
the backslashes have to be doubled.
On Macintosh,
Celestia:takescreenshot
always returns
false
because the calls to
CaptureGLBufferToJPEG
and
CaptureGLBufferToPNG
in the C++ function
celestia_takescreenshot
in
version/src/celestia/celx.cpp
are conditionally compiled out for Mac with
#ifndef TARGET_OS_MAC.
But the Celestia window can be captured with the Mac Finder.
Press shift-command-4,
press the space bar,
and click on the Celestia window.
The resulting screenshot will go on the desktop.
Another Macintosh workaround is the following.
os.execute returns only one value, an integer.
--A status of 0 indicates success.
local status = os.execute("screencapture screenshot-moon-000001.png")
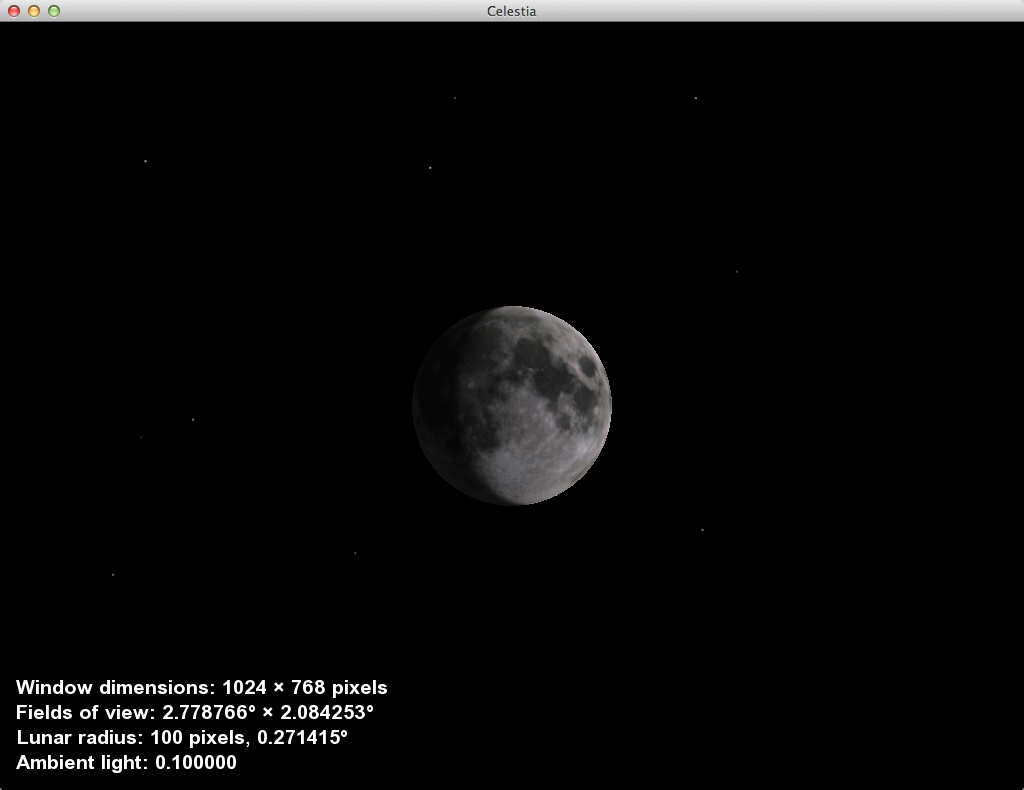
[Celestia as CCDCCD (charge-coupled device).] The ringsUranus, rings of of Uranus were discovered unexpectedly on March 10, 1977 by astronomers watching the planet pass in front of a star. A few minutes before and after the occultation, they saw the star flicker as it was blocked by the rings. Would it be possible to simulate this with Celestia?
The star was
HD 128598,
also known as SAO 158687 and
HIP
71567.
It’s not in Celestia’s database,
but we can add it by putting it into a
.stc
file.
Its spectral type is
K1IV/V
and its coördinates are
RA 14h
38m
11.811s,
Dec
–14°
57′
17.062″.
The distance of
1/.00177 =
564.971751412429
parsecs must be turned into lightyears.
Take a series of screenshots of the star passing behind the rings.
Write a Celx program that reads the pixels of the resulting
image files.
Should the star style
(Celestia:setstarstyleCelestia:setstarstyle)
be set to
"fuzzy",
"point",
or
"disk"?
Would we need a version of the file
textures/lores/uranus-rings.png
with more substantial rings?
Could we make a light curve for an eclipsing binaryeclipsing binary (star) star? (AlgolAlgol [HIP 14576] is not a binary star in the Celestia universe.) What about the silhouette of the asteroid in the Bibliography?
Maybe an antelope can see the ringsSaturn, rings of of Saturn, but a human being would need a telescope. GalileoGalileo’s telescope had a magnification of at most 30×. With this magnification, can you see that the rings of Saturn are actually rings that go around the planet?
--[[
Look at Saturn with the magnification that Galileo used.
Can you see that the rings are rings?
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hidelabel("moons", "planets") --labels can block the picture
--the night Galileo first saw the Galilean satellites of Jupiter
celestia:settime(celestia:utctotdb(1610, 1, 7, 18, 0, 0.0))
local earth = celestia:find("Sol/Earth")
local saturn = celestia:find("Sol/Saturn")
celestia:select(saturn)
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
observer:setframe(bodyfixedFrame)
local kilometers = earth:radius() + earth:getinfo().atmosphereHeight
local padua = celestia:newpositionlonglat(
math.rad(11 + 52 / 60), --east longitude is positive
math.rad(45 + 25 / 60), --north latitude is positive
kilometers / KM_PER_MICROLY)
observer:setposition(bodyfixedFrame:from(padua))
observer:lookat(saturn:getposition(), bodyfixedFrame:from(std.yaxis))
observer:trackObserver:track(saturn)
observer:setmagnificationObserver:setmagnification(30) --See magnification in lower right corner.
wait()
end
main()
Look at Saturn with Galileo’s telescope on February 17, 1613 at 17:15:00 UTC. Are the rings still visible? See edgeOn.
Christiaan HuygensHuygens, Christiaan recognized that Saturn’s rings are rings. Look at them with the magnification of 50 that he had in 1655.
By default,
the Celestia window is occupied by one big view.
This view can be
splitsplit view
horizontally or vertically by
Observer:splitviewObserver:splitview.
Each of the two resulting views has its own
Observer,
and all of the
Observers
are stored in the array returned by
Celestia:getobserversCelestia:getobservers.
This array contains only one observer
before the first call to
Observer:splitview,
and we must get a fresh copy of it after each split.
If the Celx Standard Library is has been included
(with
require("std")),
the newly created
Observer
is returned by
splitview.
Otherwise,
splitview
returns
nil.
In either case, the new
Observer
is at the end of the
getobservers
array.
At any point in
real time,
one of the views is the
active viewactive view
and the
Observer
of the active view is the
active observeractive observer.
The active observer is returned by
Celestia:getobserverCelestia:getobserver
and
Celestia:saneCelestia:sane.
--[[ Split the original view into two equal subviews, left and right. The leftObserver is the original one. The rightObserver is the new one and inherits the position and orientation of the active observer, and the frame to which the active observer has been setframed. In this example, the active observer is the original observer. (If the active observer has been setframeObserver:setframe'd, there must be a call to the waitwaitfunction between the setframe and the splitview. Otherwise, the position and orientation assertions will slightly fail.) ]] require("std") local function main() local observer = celestia:sane() observer:setposition(std.position) --vertical; 1/2 is the default local leftObserver = observer local rightObserver = leftObserver:splitview("v", 1/2) local observers = celestia:getobservers() assert(type(observers) == "table" and #observers == 2 and observers[1] == leftObserver and observers[2] == rightObserver) --After the split, the original observer is still the active observer. assert(observers[1] == celestia:getobserver()) local p1 = leftObserver:getposition() local p2 = rightObserver:getposition() assert(p1.x == p2.x and p1.y == p2.y and p1.z == p2.z) local o1 = leftObserver:getorientation() local o2 = rightObserver:getorientation() assert(o1.w == o2.w and o1.x == o2.x and o1.y == o2.y and o1.z == o2.z) local f1 = leftObserver:getframe() local f2 = rightObserver:getframe() assert(f1:getcoordinatesystem() == f2:getcoordinatesystem()) if f1:getcoordinatesystem() ~= "universal" then assert(f1:getrefobject():name() == f2:getrefobject():name()) if f1:getcoordinatesystem() == "lock" then assert(f1:gettargetobject():name() == f2:gettargetobject():name()) end end assert(leftObserver:getfov() == rightObserver:getfov()) assert(leftObserver:getspeed() == rightObserver:getspeed()) assert(leftObserver:getsurface() == rightObserver:getsurface()) local t = leftObserver:gettrackedobject() if t:name() ~= "?" and t:type() ~= "null" then assert(t:name() == rightObserver:gettrackedobject():name()) end wait() end main()
To divide the original view into three equal thirds,
pass the argument
1/3
to the first call to
splitview.
We now have left and right subviews
of width ⅓ and ⅔ respectively.
Then split the right subview in half.
--[[
Divide the original view into three equal subviews: left, center, and right.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position)
local leftObserver = observer
local centerObserver = leftObserver:splitview("v", 1/3)
local rightObserver = centerObserver:splitview("v", 1/2)
wait()
end
main()
Replace the above
wait
with the following code.
It deletes the
rightObserver’s
view,
causing the
centerObserver’s view
to fill the vacated space.
The
rightObserver
is no longer valid and must never be used again.
Observer:isvalid())
assert(#celestia:getobservers() == 3)
wait(5)
rightObserver:deleteviewObserver:deleteview()
assert(not rightObserver:isvalid())
--Ensure that no one can try to use this Observer object again.
rightObserver = nil
assert(#celestia:getobservers() == 2)
wait()
The following program splits the view into left and right subviews
for a stereoscopic, Sun’s-eye view of
SaturnSaturn.
Stare cross-eyed at the two views until you see three of them;
concentrate on the one in the center.
When you can do this comfortably,
uncomment the call to
Celestia:settimescale.
It might help if the Celestia window was not too wide.
My eyes are about
2.5
inches apart,
and so, probably, are yours.
From a point 400 millimeters in front of your eyes,
your left eye would appear to be
theta
radians away from the point between your eyes.
From the center of Saturn,
the left observer would appear to be the same angle away from the Sun.
Ditto for your right eye and the right observer.
One complication:
Celestia:newvectorlonglatCelestia:newvectorlonglat
measures longitude in the XZ plane,
but a lock frame measures it in the XY plane.
We work around the problem by copying the original position
into a temporary named
p.
The
z
coördinate is negated because the Z axis points “down”
in the XZ plane, while the Y axis points “up” in the XY plane.
--[[
Split the window into left and right subviews. Display a stereoscopic,
Sun's-eye view of Saturn and its rings and satellites.
]]
require("std")
local function main()
local observer = celestia:sane()
local sol = celestia:find("Sol")
local saturn = celestia:find("Sol/Saturn") --or try "Sol/Ida"
local lockFrame = celestia:newframe("lock", saturn, sol)
observer:setframe(lockFrame)
--distance in millimeters between user's eyes
local d = 2.5 * std.mmPerIn
local theta = math.atan2(d / 2, 400) --parallax
local sign = {-1, 1}
observer:splitview("v") --left and right subviews
for i, observer in ipairs(celestia:getobservers()) do
local p = celestia:newpositionlonglat(sign[i] * theta, 0,
12 * saturn:radius() / KM_PER_MICROLY)
local position = celestia:newposition(p.x, -p.z, p.y)
observer:setposition(lockFrame:from(position))
observer:lookat(lockFrame:from(std.position0),
lockFrame:from(std.zaxis))
end
--One rotation per 15 seconds of real time.
local rotationPeriod = saturn:getinfo().rotationPeriod
--celestia:settimescale(rotationPeriod * 24 * 60 * 60 / 15)
wait()
end
main()
When the user clicks or drags on a view, it becomes the active viewactive view. Assuming the above program with two observers, the following tick handler (tickHandler) announces when the active view has changed.
local active = nil local function tickHandler() local observers = celestia:getobserversCelestia:getobservers()
local observer = celestia:getobserverCelestia:getobserver()
local newactive = nil
if observer == observers[1] then
newactive = 1
elseif observer == observers[2] then
newactive = 2
else
errorerror (Lua function)("can't identify the active observer")
end
if newactive ~= active then
active = newactive
celestia:print("active == " .. active)
end
end
When we drag on a subview to change that observer’s position or orientation, the other subview does not change. Could we keep the two subviews in sync with each other?
Let’s display overhead and side views of the
Andromeda
GalaxyAndromeda Galaxy (M31)
(M31M31 (Andromeda Galaxy)) rotating.
Following
alternativeBodyfixed,
we provide the galaxy with a
bodyfixedFrame
whose XZ plane is the plane of the galaxy
and whose Y axis is the axis of the galaxy.
The numbers are taken from
data/galaxies.dsc.
--[[
Split the view to display overhead and edge-on views of the Andromeda Galaxy
(M31) pinwheeling. The top subview is the overhead view, occupying 3/4 of the
hight of the original view. It rotates clockwise to make the arms trail. The
bottom subview is the edge-on view, occupying 1/4 of the height of the original
view.
]]
require("std")
--variables used by the tickHander:
local m31 = celestia:find("M 31") --Messier 31 is the Andromeda Galaxy.
--[[
The orientation of the new frame for M31 with respect to its native bodyfixed
frame. The Y axis of the new frame will be the axis of the galaxy. The
180-degree rotation corrects the fact that Andromeda's bodyfixed X and Z axes
point backwards. The other rotation is taken from the data/galaxies.dsc file.
]]
local axis = celestia:newvector(-0.1274, 0.9554, 0.2663)
local angle = math.rad(142.9019)
local rotation = celestia:newrotation(axis, angle)
* celestia:newrotation(std.yaxis, math.rad(180))
local bodyfixedFrame = celestia:newframe("bodyfixed", m31, rotation)
local bottom = 1/4 --bottom view is 1/4 of height of window, top view is 3/4
local width, height = celestia:getscreendimensionCelestia:getscreendimension()
--half of the smaller dimension of the top subview
local pixels = math.min(width, height * (1 - bottom)) / 2 --in pixels
local mm = std.mmPerIn * pixels / std.pixelsPerIn --in millimeters
--How many multiples of the radius does the observer have to be away from M31 in
--order to fit it into the overhead view, assuming the default field of view?
local angularRadius = math.atan2math.atan2(mm, 400)
assert(angularRadius > 0)
local multiples = 1 / math.sinmath.sin(angularRadius)
local distance = multiples * m31:radius() / KM_PER_MICROLY
local position = {
{celestia:newposition(-distance, 0, 0), std.yaxis}, --edge-on
{celestia:newposition(0, distance, 0), std.xaxis} --overhead
}
local t0 = celestia:getscripttime()
local seconds = 60 --number of real-time seconds per rotation
local function tickHandler()
--Make M31 seem to spin by rotating the observer around it.
local theta = 2 * math.pi * (celestia:getscripttime() - t0) / seconds
local rotation = celestia:newrotation(-std.yaxis, theta) --arms trail
for i, observer in ipairs(celestia:getobservers()) do
local observerPosition = rotation:transform(position[i][1])
observer:setposition(bodyfixedFrame:from(observerPosition))
local up = rotation:transform(position[i][2])
observer:lookat(m31:getposition(), bodyfixedFrame:from(up))
end
end
local function main()
--horizontal split, one subview atop another
local observer = celestia:sane()
observer:splitview("h", bottom)
--celestia:setwindowbordersvisibleCelestia:setwindowbordersvisible(false) --uncomment & see what happens
celestia:hide("constellations", "ecliptic", "grid")
celestia:hidelabel("galaxies") --interferes with view of galactic center
celestia:select(m31)
for i, observer in ipairs(celestia:getobservers()) do
observer:setframe(bodyfixedFrame)
end
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Add a third observer to the above program: front, side, top.
To try to make the front and top views more isometric, I positioned the observers far away and magnified the galaxy by narrowing the field of view. But this made the galaxy look like a quasarquasar, with a core that outshone the rest of the object. Is there a solution?
Small multiples [a series of diagrams in the same format] resemble the frames of a movie: a series of graphics, showing the same combination of variables, indexed by changes in another variable.
Small multiples are economical: once viewers understand the design of one slice, they have immediate access to the data in all the other slices. Thus, as the eye moves from one slice to the next, the constancy of the design allows the viewer to focus on changes in the data rather than on changes in graphical design.
Let’s display a series of snapshots of the phases of
Venus.
As we saw in the above program,
each observer can have his own position and orientation.
Each one can also have his own
simulation time;
see
Observer:gettime.
But a simpler way to display the phases
is to keep the times the same
and give each observer a different position with respect to Venus.
At the time of superior conjunctionsuperior conjunction, the Earth and Venus are on opposite sides of the Sun, and we would see a “full Venus” if the Sun’s glare was not blocking our view. At inferior conjunctioninferior conjunction, about 10 months later, the Earth and Venus are on the same side of the Sun and we would see a “new Venus”. See solarDays for the approximate intervals between the conjunctions, and findZero for the exact intervals.
The following program takes snapshots of Venus at eight times
during this 10-month interval.
The array
fractions
gives the fraction of the interval that has elapsed
at the time of each snapshot;
the values were chosen for æsthetic effect.
For each fraction,
we compute the position of the Earth in relation to Venus at that time.
Then we place an observer at that same position
with respect to the present Venus.
To divide the original view into eight subviews of equal width,
we first pass the argument
1/8
to the first call to
splitviewObserver:splitview.
This divides the original view into subview of width
1/8
on the left,
and
7/8
on the right.
Then we split the right subview with an argument of
1/7.
The final subview is prevented
by the
if
statement from being split.
--[[
Splitview: show the phases of Venus as seen from the Earth.
The full Venus is on the left, the new Venus on the right.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("constellations", "ecliptic", "galaxies", "grid")
celestia:hidelabel("planets")
celestia:settimescale(0)
--conjunctions of Venus with the Sun, as seen from the Earth
local t0 = celestia:utctotdb(2014, 10, 25, 6, 52, 53) --superior
local t1 = celestia:utctotdb(2015, 8, 13, 19, 15, 32) --inferior
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local venus = celestia:find("Sol/Venus")
local lockFrame = celestia:newframe("lock", sol, venus)
observer:setframe(lockFrame)
observer:setfov(math.rad(4/60)) --4 minutes of arc
local fractions = {0, 1/2, 2/3, 3/4, 4/5, 5/6, 9/10, 19/20}
for i, fraction in ipairs(fractions) do
local observer = celestia:getobservers()[i]
local t = t0 + fraction * (t1 - t0)
local position = lockFrame:to(earth:getposition(t), t)
observer:setposition(lockFrame:from(position))
observer:lookat(venus:getposition(), std.yaxis)
if i < #fractions then
observer:splitview("v", 1 / (#fractions - i + 1))
end
end
wait()
end
main()
Display a series of views of a lunar eclipse as seen from a point on the ground at intervals of 20 minutes.
Display two parallel series of views of a solar eclipse, as seen from two points on the ground.
Split the window into rows and columns. Display a calendar of the current month showing the phase of the Moon for each day.
[The interstellar cruiser had] a complicated calculating machine which could throw on the screen a reproduction of the night sky as seen from any given point of the Galaxy.…
“Do you see that dark nebula? … Watch it. I’m going to expand the image.”
Pritcher had watched the phenomenon of Lens Image expansion before but he still caught his breath.…
“We’re in space now, about to make the first hop.”
Pritcher, in sudden horror, sprang to the visiplate.… “By whose order?”
“You probably felt no acceleration, because it came at the moment I was expanding the field of the Lens and you undoubtedly imagined it to be an illusion of the apparent star motion.”
We sped through one day of simulation time in celestialSphere, watching the Earth make one full turn. But instead of that program’s jackrabbit start and the screeching halt, it would be more natural to ramp the timescale up and down gradually. The curve of the ramp will be the graph of the following function, shown with its derivative.
| f(x) | = | –2x3 + 3x2 |
| f′(x) | = | –6x2 + 6x |
The function was carefully engineered to increase gradually along the interval
[0, 1],
f(0) = 0
f(1) = 1
while being flat at both ends.
f′(0) = 0
f′(1) = 0
We evaluate
f
indirectly by calling the function
std.splinestd.spline.
It translates and scales
f
horizontally and vertically to the desired values.
In the following program,
the horizontal axis is the real time in seconds and goes from 0 to 3;
the vertical axis is the timescale and goes from 1 to
60 · 60.
The first argument of
std.spline
is the current time.
The next two arguments are the starting and ending times
of the interval during which the value will ramp up (or down) gradually.
The current time must be between (or equal to) these two times.
The next two arguments are the starting and ending values
of the quantity that we want to ramp up (or down).
The return value is the value of the quantity at the current time.
std.spline
is applicable to any change of timescale, zoom level,
position, orientation, etc.
Apple iOS programmers know it as
UIViewAnimationOptionCurveEaseInOutUIViewAnimationOptionCurveEaseInOut (iOS enumeration);
Android programmers as
AccelerateDecelerateInterpolatorAccelerateDecelerateInterpolator (Android class).
Here is the program from
celestialSphere,
taking three seconds of real time to come up to high speed.
Celestia:getscripttimeCelestia:getscripttime
returns the number of real-time seconds since the Celx program started running.
--[[
Watch one rotation of the Earth at high speed. The tickHandler holds the
observer above the point where the subsolar meridian crosses the equator.
The Earth speeds up gradually, fast-forwards through one day, and slows down
gradually.
Phase 1 lasts until the "CELESTIA" logo disappears. During this phase, the
timescale remains constant at 1.
Phase 2 lasts 3 seconds of real time. During this phase, the timescale goes
from 1 to 60*60.
Phase 3 lasts 24 hours of simulation time. During this phase, the timescale
remains constant at 60*60.
Phase 4 lasts 3 seconds of real time. During this phase, the timescale goes
from 60*60 to 1.
Phase 5 last forever. During this phase, the timescale remains constant at 1.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local normalScale = 1
local fastScale = 60 * 60 --one hour of simulation time per second of real time
local rampLength = 3 --seconds of real time
local phase = nil
local start2 = nil --start of phase 2 in real time
local start3 = nil --start of phase 3 in simulation time
local start4 = nil --start of phase 4 in real time
local sol = celestia:find("Sol")
local earth = celestia:find("Sol/Earth")
local bodyfixedFrame = celestia:newframe("bodyfixed", earth)
local lockFrame = celestia:newframe("lock", earth, sol)
local microlightyears = 5 * earth:radius() / KM_PER_MICROLY
local function tickHandler()
--one hour of simulation time per second of real time.
if phase == 2 then --speed up
local t = celestia:getscripttime() - start2
if t < rampLength then
local scale = std.spline(t, 0, rampLength,
normalScale, fastScale)
celestia:settimescaleCelestia:settimescale(scale)
else
start3 = celestia:gettime()
phase = 3
celestia:settimescale(fastScale)
end
elseif phase == 3 then --fast forward
if celestia:gettime() >= start3 + 1 then
start4 = celestia:getscripttime()
phase = 4
end
elseif phase == 4 then --slow down
local t = celestia:getscripttime() - start4
if t < rampLength then
local scale = std.spline(t, 0, rampLength,
fastScale, normalScale)
celestia:settimescale(scale)
else
phase = 5 --slow-down completed, back to normal speed
celestia:settimescale(normalScale)
end
end
--unit vectors in universal coordinates
local toNorthPole = bodyfixedFrame:from(std.yaxis)
local toSol = lockFrame:from(std.xaxis)
local v = toNorthPole:erect(toSol)
local position = earth:getposition()
observer:setposition(position + microlightyears * v)
observer:lookat(position, toNorthPole)
end
local function main()
--clouds distracting, ecliptic irrelevant
celestia:hide("cloudmaps", "cloudshadows", "ecliptic")
celestia:show("boundaries") --of constellations
earth:addreferencemark({type = "body axes"})
earth:addreferencemark({type = "planetographic grid"})
observer:setframe(lockFrame)
phase = 1
celestia:registereventhandler("tick", tickHandler)
wait(std.logo)
start2 = celestia:getscripttime()
phase = 2
wait()
end
main()
It takes three seconds of real time for the above program to increase the timescale from to to 60 · 60. How much simulation time passes during this interval?
The area under our original curve
f(x)
=
–2x3 +
3x2
from
a = 0
to
b = 1
is
1
∫
0
f(t) dt
=
1
∫
0
–2t3
+ 3t2 dt
=
–
1
2
t4
+
t3
|
|
|
|
|
1
0
=
1
2
–
0
=
1
2
See the review of Calculus in
Exponential.
The curve f
has been stretched horizontally by a factor of 3,
and vertically by a factor of
60 · 60 − 1,
to form the following curve
g
returned by
std.spline.
It has also been raised by 1 unit.
g(x)
=
1 + (60 · 60 − 1)f(
x
3
)
The area under g from a = 0 to b = 3 is therefore 3 · (60 · 60 − 1) times the area under f, plus 3 · 1. 3 · (60 · 60 − 1) 1 2 + 3 = 5401.5 This area represents the number of seconds of simulation time that passes during the three seconds of real time. It’s about 90 minutes.
Print the simulation time at the start of phases 2 and 3. Does the number of seconds of simulation time between these two points agree with the above calculation? Run the program several times and take the average.
Create a five-minute Celestia show to be projected onto a planetarium dome to orient and hold the attention of the audience while they sit down and adjust to the darkness. For example, show the Galilean satellites of Jupiter during the current 24 hours, the phases of the Moon during the current week, the motion of the Sun in front of the zodiac during the current month, the phases of Venus and the retrograde motion of Mars during the current year, and the inclination of the rings of Saturn during several years. There could be geophysical information, too, such as tides and weather from the NOAA website.
Decide if the information should be presented as a table of numbers,
a series of still images,
or a motion picture.
For example, to show whether the days are getting longer or shorter this week,
you could display a table of the sunset times for your locality.
Or you could project a series of pictures,
at intervals of one week,
of the Earth at 6:00 p.m. local time.
The series would show the Earth
leaning farther and farther into, or away from, the Sun.
Be sure to turn on the
nightmaps
renderflag.
Bring up the reference lines—meridian, ecliptic, celestial equator—and swing the Zeiss into the initial orientation. Orrery in position, projectors and amplifiers up. Laser pointer in breast pocket, mag light in belt holster. Launch the Celx program, cue Mozart’s Eine kleine Nachtmusik, open the outer doors. It’s showtime!
There are many reasons to compile your own Celestia from the source code.
Have you ever wanted to modify Celestia?
For example,
it would be great if we could pass command line arguments to a Celx script,
or make the Lua function
print
in Microsoft Windows Celx produce standard output.
We could even comment out that five-second CELESTIA logo upon startup.
Have you ever wanted to modify the Celx language that Celestia accepts?
It would be great if Celx had a function for setting the size of the window.
Have you discovered a bug in Celestia?
Or are you simply interested in dissecting a large, well-written program
in C++ and OpenGL?
To compile Celestia on a Mac,
you will need the application
Xcode.
I used Xcode version 8.3.4 on macOS Sierra 10.12.4.
Go to the Celestia download page
http://www.shatters.net/celestia/download.html
and click on “Celestia 1.6.1 Source Code”
to get the source code file,
currently
version.tar.gz.
Double-click on it to create a folder named
version.
Go into its
macosx
subfolder and double-click on the file
celestia.xcodeproj
to open the
celestia
project in Xcode.
The left panel of Xcode is the Project Navigator.
To see it, select
View → Navigators → Show Project Navigator.
The top (or only) item in the Project Navigator is the
celestia
project.
Click on its triangle to open it
and display the folders and files it contains.
Two of the files have to be modified by hand to get them to compile.
Open the
Celestia Main
and
celmath
folders and edit the file
intersect.h.
Insert the following line after the three existing includes.
Then open the
Classes
and
Wrappers
folders and edit the file
MacInputWatcher.h.
Change the forward declaration
@class _MacInputWatcher;
to the following.
#ifdef __cplusplus //two underscores class _MacInputWatcher; //forward declaration in the language C++ #else @class _MacInputWatcher; //forward declaration in the language Objective-C #endif
A third file has to be modified to avoid a runtime warning about a non-existent
~/.celestia.cfg
file.
Open the
Celestia Main
and
celestia
folders and edit the
celestiacore.cpp
file.
In the member function
CelestiaCore::initSimulation,
change
to
//if the file ~/.celestia.cfg exists and is readable, if (ifstream(localConfigFile.c_str()).good())
After editing the three files,
select the
celestia
at the top of the Project Navigator.
This should cause
the large central panel of Xcode to display a subpanel on the left,
listing one project and three targets.
If you do not see this subpanel, click on the square icon
at the start of the second line of the central panel.
Select the project
celestia
(lowercase c)
in the subpanel.
Select Build Settings at the top of the central panel
and the Architectures inside the Architectures section farther down.
Change Architectures from
“Standard Architectures (64-bit Intel) (x86_64) $(ARCHS_STANDARD)”
to
“32-bit Intel i386 - $(ARCHS_STANDARD_32_BIT)”.
We have to do this because the
libpng.dylib
and
liblua.dylib
that come with the project do not contain the architecture
x86_64.
On the next line, the Base SDK is currently set to
MacOSX10.4u.sdk.
Change it to one of the macOS SDKs that are present on your machine,
e.g., “Latest macOS”.
Select the target
Celestia
(uppercase C)
in the subpanel on the left.
Select
Build Settings → Deployment → Deployment Postprocessing
and set it to Yes.
This will create the
CelestiaResources
folder inside of the
Celestia.app/Contents/Resources
folder.
In the upper left corner of Xcode, above the word “Scheme”,
select the target
Celestia.
Pull down the Product menu and select Build.
Ignore the hundreds of yellow warnings.
To find the folder
Celestia.app
created by the Build,
go to the Project Navigator,
open the Products folder,
control-click on
Celestia.app,
and select Show in Finder.
You can then control-click on the
Celestia
in the Finder and select Get Info.
My
Celestia.app
folder turned out to be located in the folder
/Users/myname/Library/Developer/Xcode/DerivedData
where
/celestia-ewypizctgfcymhfbfsanjfzopdon/Build/Products/Developmentmyname
is my name,
and the long random string was made up by Xcode.
Your name and string will be different.
Open the Terminal app and look at the
Celestia
executable you just created.
cd $HOME/Library/Developer/Xcode/DerivedData\ /celestia-ewypizctgfcymhfbfsanjfzopdon/Build/Products/Development pwd ls -l Celestia.app cd Celestia.app/Contents/MacOS pwd ls -l Celestia
To make it possible to run this executable just by typing its name,
put the name of its directory into your
PATH
environment variable.
echo $PATH export PATH=$PATH:`pwd` echo $PATH which Celestia
The create a
.celx
file in the Celx directory and run it.
cd ../Resources/CelestiaResources
pwd
echo 'celestia:print("hello", 10)' > myprog.celx
ls -l myprog.celx
Celestia myprog.celx
Celestia then runs correctly except for the following extraneous error message:
“Error opening config file
'/Users/myname/Library/Application Support/CelestiaResources/celestia.cfg'.”
Here’s what causes the message.
The Objective-C method
setupResourceDirectory
in the file
CelestiaController.m
in the folder
Classes
creates a directory named
/Users/myname/Library/Application Support/CelestiaResources,
and adds this directory to the list of
existingResourceDirs
in the
NSUserDefaults.
But
setupResourceDirectory
does not put any file named
celestia.cfg
into the directory.
Later, the method
initSimulation
in
version/macosx/CelestiaAppCore.mm
looks for a file named
celestia.cfg
in each of the
existingResourceDirs.
To avoid the error message,
I simply commented out the statement in
setupResourceDirectory
that adds the directory to the
existingResourceDirs.
To compile Celestia on my Windows 7 Home Premium,
I downloaded Microsoft Visual C++ 2010 Express
from
http://www.microsoft.com/visualstudio/eng/downloads#d-2010-express
and installed it into the directory
C:\Program Files (x86)\Microsoft Visual Studio 10.0\.
Two of the libraries that come with Celestia,
zlib
and
libpng,
are not compatible with this version of Visual C++.
We will have to recompile them from their source code.
First,
download the file
http://zlib.net/zlib127.zip
and place the resulting folder
zlib-1.2.7
on your Desktop.
Then download the file
libpng1514.zip
from
http://sourceforge.net/projects/libpng/files/libpng15/1.5.14/
and place the folder
lpng1514
on your Desktop.
Following the instructions in
lpng1514\projects\vstudio\readme.txt,
edit the file
lpng1514\projects\vstudio\zlib.props
with WordPad and change the directory name
..\..\..\..\zlib-1.2.5
to
..\..\..\..\zlib-1.2.7.
Double-click on the
“solution”
file
lpng1514\projects\vstudio\vstudio.sln
to open it in Visual C++ Express 2010.
In the left panel of Visual C++,
called the Solution Explorer,
right-click on
libpng
and select Properties.
Press the Configuration Manager button and change
libpng
from Debug to Release;
then press Close to exit from the Configuration Manager.
Select
Configuration Properties → General → Project Defaults
and change the Configuration Type of
libpng
from Dynamic Library
(.dll)
to
Static library
(.lib).
In the Solution Explorer,
right-click on
libpng
and select Build.
The bottom panel of Visual C++ should say
1> zlib.vcxproj -> C:\Users\Myname\Desktop\lpng1514\projects\vstudio\Debug\zlib.lib etc. 3> libpng.vcxproj -> C:\Users\Myname\Desktop\lpng1514\projects\vstudio\Release\libpng15.lib ========== Build: 3 succeeded, 0 failed, 0 up-to-date, 0 skipped ==========
Go to the Celestia
download page
and download the source code file
version.tar.gz.
(To open this file,
I downloaded
7-Zip
from
www.7-zip.org
and installed it in the directory
C:\Program Files (x86)\7-Zip.)
Place the folder
version
on your Desktop.
Open the solution file
version\celestia.sln
with Visual C++.
Since
celestia.sln
is only a Visual C++ Express 2008 file,
it gets converted automatically to 2010.
Welcome to the Visual Studio Conversion Wizard.
Next
•Yes, create a backup before converting.
Next
Finish
Move or copy the two libraries you created into the Celestia directories.
First go to the directory
C:\Users\Myname\Desktop\version\windows\lib\x86\
and rename the file
zlib.lib
to
oldzlib.lib.
Then copy the new files
C:\Users\Myname\Desktop\lpng1514\projects\vstudio\vc10\Debug\zlib.lib
and
C:\Users\Myname\Desktop\lpng\projects\vstudio\Release\libpng15.lib
to the directory
C:\Users\Myname\Desktop\version\windows\lib\x86\.
The file
C:\Users\Myname\Desktop\lpng1514\png.c
says that the current version of libpng is 1.5.14.
Edit Celestia’s
png.h
file to agree with these numbers.
In the Solution Explorer,
open
celestia → External Dependencies.
Unfortunately,
you will see two
png.h
files.
Right-click on each one to see its Properties,
including its full pathname.
The one we want to edit is
C:\Users\Myname\Desktop\version\windows\inc\libpng\png.h,
not
macosx\png.h.
In the
png.h
file,
update the six macros
PNG_LIBPNG_VER_STRING,
PNG_HEADER_VERSION_STRING,
PNG_LIBPNG_VER_MAJOR,
PNG_LIBPNG_VER_MINOR,
PNG_LIBPNG_VER_RELEASE,
and
PNG_LIBPNG_VER.
Then pull down the Visual C++ File menu and select Save png.h.
The header file
C:\Program Files (x86)\Microsoft SDKs\Windows\v7.0A\include\windef.h
defines the macro
FAR,
so there is no need for the file
version/windows/inc/libjpeg/jmorecfg.h
to define it again.
In the Solution Explorer,
open
celestia →
External Dependencies →
jmorecfg.h.
At line 212 of this file,
change
to
/* Define the macro FAR only if it is not already defined. */ #ifndef FAR #ifdef NEED_FAR_POINTERS #define FAR far #else #define FAR #endif #endif
In the Solution Explorer,
right-click on celestia
and select Properties.
Press the Configuration Manager button and change
celestia
from Debug to Release.
You will also have to change the following five properties.
$(ProjectName).
$(ProjectName).exe
to
$(OutDir)$(TargetName)$(TargetExt).
While you are making this change,
you can press the Macros button to see the values of these macros.
For example, the
OutDir
macro should be
C:\Users\Myname\Desktop\version\Release\.
libpng.lib
to
libpng15.lib
(“fifteen”).
Use Link Time Code Generation (/LTCG).
$(TargetPath)
to
"$(ProjectDir)$(TargetFileName).
In the Solution Explorer,
right-click on celestia
and select Build.
According to the
ProjectDir
macro,
the project directory is
C:\Users\Myname\Desktop\version\.
Move or copy the dynamic-link libraries from
C:\Users\Myname\Desktop\version\windows\dll\x86\
to the project directory.
Move or copy the executable file
celestia.exe
from
version\Release
to the project directory.
Run the executable file
celestia.exe
by double clicking on it.
To run a
.celx
program in the Windows Command Prompt window
with your freshly compiled Celestia,
associate a file type with the
.celx
extension.
Right-click on Command Prompt and select Run as administrator.
The caret
(^)
is the continuation character.
The most prestigious distribution of Linux is Red Hat. But Red Hat costs money, so we’ll use Fedora Linux instead. My Fedora has no idea that it’s just a “brain in a vat”. It thinks it’s installed on a real computer, but it’s actually installed in Oracle VM VirtualBox, an application running on my daughter’s Microsoft Windows PC. Here are the Fedora’s specs.
uname -a Linux localhost.localdomain 3.3.4-5.fc17.x86_64 #1 SMP Mon May 7 17:29:34 UTC 2012 x86_64 x86_64 x86 64 GNU/Linux g++ -v gcc version 4.7.0 20120507 (Red Hat 4.7.0-5) (GCC)
To install the packages for
the languages C, C++, and Perl,
I became the superuser and gave the following Fedora commands.
Other distributions of Linux
might have to use
yast
or
rpm
instead of
yum.
The shellscript below runs Celestia’s
configure
command.
To get
configure
to run correctly,
I had to give additional names to three files
in the directory
/usr/lib64.
Here’s why.
configure
runs the C compiler
gcc,
which runs the linker
ld.
The
-lz
option of
ld
told it to look for a “shared object” library named
libz.so,
so I had to give that name to the existing file
libz.so.1.2.5.
Similarly, I had to give the additional name
libjpeg.so
to the existing file
libpng15.so.15.10.0.
Finally,
ld
looked for the function
png_create_info_struct
in a file named
libpng.so.
There was no such file, but
nm -D
told me that the function was in another file named
libpng15.so.15.10.0.
I therefore gave the additional name
libpng.so
to this file.
I bestowed these additional names by
becoming the superuser and creating three symbolic links
with the command
ln -s.
Celestia’s
configure
command will create a
config.log
file.
If this log says that a file is missing,
use the following command to discover which package would provide that file.
I discovered that the following packages needed to be installed.
yum install mesa-libGL-devel for /usr/include/GL/gl.h yum install mesa-libGLU-devel for /usr/include/GL/glu.h yum install glut-devel for /usr/include/GL/glut.h yum install lua-devel for /usr/include/lua.h yum install zlib-devel for /usr/include/zlib.h yum install libjpeg-devel for /usr/include/jpeglib.h yum install libpng-devel for /usr/include/png.h yum install libgnomeui-devel for libgnomeui-2.0.pc in gnome celestia yum install PackageKit-gtk3-module so gnome Celestia can load pk-gtk-module yum install gtk2-devel for gtk+-2.0.pc in gtk Celestia yum install gtkglext-devel for gtkglext-1.0.pc in gtk Celestia yum install libtheora-devel so gtk Celestia can say File → Capture Movie… yum install libXt-devel for /usr/include/X11/Intrinsic.h yum install kdelibs3-devel for /usr/include/kde/kdesharedptr.h yum install qt3-devel for /usr/lib64/qt-3.3/include/private/qucomextra_p.h yum install kdebase so KDE Celestia can say Help → Celestia Handbook
The following shellscript downloads the Celestia source code
and compiles it on Fedora.
Run the shellscript as the superuser.
According to Celestia’s
README
and
INSTALL
files,
Celestia can be compiled with one of four possible
graphical interfaces: GLUT, GNOME, GTK, and KDE.
Uncomment the line for the interface you want.
It will create one of four possible
bin
directories and one of four possible Celx directories.
Try GLUT first because it’s the simplest:
the resulting Celestia
doesn’t even have menus.
The most complicated interface is KDE.
Fedora downloads a file from the web with the
curl
command;
other distributions of Linux might use
wget.
Some of the Celestia source files have to be tweaked a bit.
The shellscript edits them by invoking
Perl,
being careful never to change the newline characters in the file.
This keeps the line numbers undisturbed.
Following the instructions in
README,
the shellscript then tries to run Celestia’s
configure
command.
To see what
configure
will try to do,
run
./configure --help.
To see what configure was able to do,
and what stopped it dead,
look at the
config.log
file.
It lists the names of the files that are missing
because they belong to packages that have not yet been installed.
Many of these files will be
.h
(“header”)
files.
In GLUT and KDE,
the linker said that the archive file
celengine/libcelengine.a(libcelengine_a-render.o)
had an undefined reference to
glDepthFunction.
The linker then helpfully offered the information
that this function was defined in the library
/lib64/libGL.so.1.
I therefore gave the
-lGL
option to the linker.
Now stop being the superuser and run the Celestia executable.
/usr/local/glut/bin/celestia or gnome, gtk, kde
In GLUT Celestia,
press
i
for clouds and
control-l
(lowercase L)
for the night lights when you see the Earth.
GLUT Celestia needs command line argument
-f
before the name of the Celx file.
In GNOME Celestia,
every celestial object is initially invisible and the window is black.
Pull down
Options →
View Options…
and turn everything on.
Check all the checkboxes,
set Texture Detail to high, etc.
In KDE Celestia,
the Follow Earth button places us
one milliparsec
(approximately 206.27 astronomical units)
from the Earth
because the bookmark’s
cel:
URL in
version/src/celestia/kde/data/bookmarks.xml
has its coördinates measured with respect to an obsolete frame of reference
whose origin is one milliparsec from the Sun.
For example, the
x
coördinate is encoded
(bits128)
as the string
0E0JDZAWdoDCDA,
representing
3266.50180188195 microlightyears
or approximately 206 astronomical units.
The following shellscript compiles Celestia on Solaris, a representative non-Linux version of Unix. We compile it only with GLUTGLUT (OpenGL Utility Toolkit), the simplest visual interface. We also compile Lua and GLUT from their source code. We’ll use the GNU C and C++ compilers that came on the October 2009 Solaris 10 distribution DVD.
uname -a SunOS unknown 5.10 Generic_141445-09 i86pc i386 i86pc g++ -v gcc version 3.4.3 (csl-sol210-3_4-branch+sol_rpath)
The command line option
-lGL
tells the linker to link in the shared object library
/usr/lib/libGL.so.
Without it, the linker complains that the function
glPointSize
is missing.
To verify that this library contains the function,
we can examine the library’s name table
with the Unix program
nm.
Append the name of the directory that holds the GLUT man pages
to the environment variable
MANPATH.
Before launching Celestia,
append the name of the directory that holds
libglut.so
to the environment variable
LD_LIBRARY_PATH.
When you see the Earth, press i for clouds and control-l (lowercase L) for night lights.
The current version of Celestia (1.6.1) incorporates version 5.1.4 of Lua. If a future Celestia moves up to Lua 5.2, here are the changes that will have to be made in the software in this book.
coroutine.running
returns one value in Lua 5.1, two values in Lua 5.2.
See
luaHookFunctions.
write
method of
io
returns a
boolean
in Lua 5.1,
and a file descriptor in Lua 5.2.
See
standardOutput.
bits32.lshift.
See
inputFile.
"\xFF".
Lua 5.1 makes us write it in decimal as
"\255".
See
inputFile.
math.log
and
math.log10;
Lua 5.2 has a two-argument
math.log.
See
loopDatabase,
hertzsprungrussell,
celestialDome,
Object:absmag,
and the initialization of the constant
std.significant
in the standard library in
stdCelx.table.unpack;
Lua 5.1 doesn’t.
See the workaround in
traceRetrograde
and in the function
std.tourl
in the standard library in
stdCelx.
string.format
can format a
boolean
with the option
"%s";
the Lua 5.1 can’t.
See
screenShot.os.execute
returns one value in Lua 5.1,
two values in Lua 5.2.
See
screenShot.
module
and
package.seeall;
Lua 5.2 doesn’t.
See the start of the standard library in
stdCelx.
A Unix system can run a script in any interpreted language:
php
or
python
for younger programmers,
bash
or
perl
for the author of this book.
The name of the interpreter program for the given language
is written after the
#!
on the first line of the program.
Let’s make this work for Celx too.
#!/bin/celestia
--[[
This file is named myprog.celx. It demonstrates the #! line.
The #!/bin/celestia must be written on the first line of this file.
There must be no blanks, tabs, or comments before or above the #!/bin/celestia.
]]
require("std")
local function main()
--Keep the Sun in view, but get away from its glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:print("Hello, world!")
wait()
end
main()
We will make it possible to run the above program with the following one-word command line.
myprog.celx
The above command will actually run the following C program.
The C program splits itself into two
processesprocess (in Unix)
called the
parentparent process (in Unix)
and
childchild process (in Unix).
The child copies the file
myprog.celx, minus the first line,
into a temporary file whose name is composed by the Unix
tmpnam
function.
This temporary file is a legal Celx program,
now that the first line has been chopped off.
The child then transforms itself into the Celestia application
with the Unix
execl
function.
In its new identity as Celestia,
the child reads and executes the temporary file.
Meanwhile, the Unix
waitpid
function causes the parent to sink into a stupor.
When the child has finished its life,
the parent wakes up,
removes the temporary file created by the child,
and commits suicide.
This family drama is necessary to ensure that the temporary file will always be removed. The child cannot erase the file: the child has metamorphosized into Celestia, and Celestia does not erase files. And even if the child could erase the file, there is always the possibility that the child will crash before it has done so. The purpose of the parent is to remain in the background until the death of the child, and then to remove the temporary file containing the decapitated Celx program.
/* This file is a C program named decapitator.c. */
#include <stdio.h> /* for tmpnam and perror */
#include <stdlib.h> /* for exit */
#include <signal.h> /* for signal */
#include <sys/types.h> /* for fork, waitpid */
#include <unistd.h> /* for fork, unlink */
#include <sys/wait.h> /* for waitpid */
void cleanup(int s);
char temp[L_tmpnam + 5]; /* name of temporary file */
int main(int argc, const char *const *argv)
{
pid_t pid;
int status;
if (argc < 2) {
fprintf(stderr, "%s: missing command line argument\n", argv[0]);
return EXIT_FAILURE;
}
sprintf(temp, "%s.celx", tmpnam(NULL));
if (signal(SIGINT, cleanup) == SIG_ERR || (pid = fork()) < 0) {
perror(argv[0]);
return EXIT_FAILURE;
}
if (pid == 0) {
/* Arrive here if I am the child.
Copy the .celx program, minus the first line, into temp. */
FILE *in, *out;
int seenNewline = 0;
int c;
if ((in = fopen(argv[argc - 1], "r")) == NULL
|| (out = fopen(temp, "w")) == NULL) {
perror(argv[0]);
return EXIT_FAILURE;
}
while ((c = fgetc(in)) != EOF) {
if (seenNewline) {
fputc(c, out);
} else if (c == '\n') {
seenNewline = 1;
}
}
fclose(in);
fclose(out);
/* -f option needed only if celestia compiled --with-glut */
execl("/full/pathname/of/the/celestia/application",
"celestia", "-f", temp, (char *)0);
/* Arrive here if execl failed. */
perror(argv[0]);
return EXIT_FAILURE;
}
/* Arrive here if I am the parent. Wait for my child to die. */
waitpid(pid, &status, 0);
if (unlink(temp) == 0 && WIFEXITED(status)) {
/* We were able to erase the temporary file, and Celestia
returned an exit status. Return the exit status. */
return WEXITSTATUS(status);
}
/* We were unable to erase the temporary file,
or Celestia failed to return an exit status. */
return EXIT_FAILURE;
}
void cleanup(int signalNumber)
{
/*
Arrive here if the script was interrupted by a control-c (SIGINT).
The exit status of the script will be the signal number.
*/
unlink(temp);
exit(signalNumber);
}
Before compiling the above C program,
change the
full/pathname/of/the/Celestia/application
to the full pathname of the Celestia application on your machine.
You must also remove the
"-f"
if your Celestia application was not compiled with
GLUT
(see
compileLinux
and
solaris).
Then compile the C program and name the resulting executable
/bin/celestia.
The following command will list the names of the directories in your
PATH
environment variable.
Put
myprog.celx
into one of these directories.
Then make the file
myprog.celx
executable by turning on its
r
and
x
mode bits (read and execute,
rwxr-xr-x).
You should now be able to run
myprog.celx
just by typing its name.
If
myprog.celx
produces standard output with the
print
in
standardOutput
and
os.exit
in
osExit,
you can capture this output with the following command line.
The Lua Reference Manual lists the data types, global variables, and functions in the language Lua. The language Celx is a superset of Lua. This appendix lists the classes, global variables, and functions that Celestia has added to Lua to create Celx.
The Celx Standard Library in
standard
and
stdCelx
adds even more features to the language.
They include additional methods for the classes
and modifications of some of the existing methods.
In this appendix,
these methods are tagged with the words (Added) and (Modified).
The standard library also creates one global variable,
a table named
std
containing variables and functions.
type
to be
"userdata".
Celestia,
the object that lets us create all the other Celx objects.Celscript,
representing a script in the language Cel.Font,
used by
Celestia:print
and the OpenGL functions.Frame,
a (possibly moving) frame of reference in the Celestia universe.
The Celx Standard Library implements an enhanced
“rotated frame” as a table containing a
Frame
and a
Rotation.Observer,
a point of view in the Celestia universe.Object,
a celestial object: planet, star, spacecraft, etc.Phase,
a portion of the lifetime of a celestial object.Position,
an
(x, y, z)
position measured with respect to a frame of reference.Rotation,
a rotation,
consisting of an axis and an angle.
A
Rotation
can also represent an orientation.
Texture,
an image file displayed by OpenGL.Vector,
an invisible arrow with a length and a direction,
expressed by
(x, y, z)
coördinates measured with respect to a frame of reference.celestia,
an object of class
Celestia.
There is one such object in each Celx file.
See
objectsAndClasses.KM_PER_MICROLY,
the number of kilometers per microlightyear
(9,460,730.4725808).
See
lightyear.gl,
a table of functions and arguments belonging to the
OpenGL Graphics Library.
See
opengl.glu,
a table of functions belonging to the
OpenGL
Utility Library
(GLU).
See
opengl.std,
a table of the variables and functions belonging to
the Celx Standard Library.
This table is present only if the Celx program calls
require("std").
wait,
to let Celestia advance the simulation time and update the window.
See
wait.
celestia_keyboard_callback,
called when a character key is pressed.celestia_cleanup_callback,
called when the Celx program is finished.
A Celx file has exactly one object of class
Celestia.
It is named
celestia.
This object is the program’s interface to Celestia,
and is the means by which all the other Celx objects are created.
There is no way to create or destroy this object;
it already exists when the Celx program starts running.
See the
celestia
object for details about its status as a
singleton.
Class
Celestia
is implemented in
version/src/celestia/celx.cpp.
Create a
Celscript
object that can be executed by
Celscript:tick.
See also
Celestia:runscript.
Return an iterator for looping through all the deep sky objects in the
DeepSkyCatalogs
in
celestia.cfg.
See
loopDatabase
for an example.
See also
Celestia:getdso
and
Celestia:getdsocount.
Return the celestial
Object
with the given name (case-insensitive).
The
Objects
are listed in the following files in
celestia.cfg:
the
StarDatabase
and the additional
StarCatalogs;
the
SolarSystemCatalogs,
which include extrasolar planets;
and the
DeepSkyCatalogs.
A constellation is not an
Object,
so it cannot be found.
If there are no stars within one lightyear of the active
Observer,
the argument of
Celestia:find
must be the full pathname of the desired object:
"Sol/Earth/Moon".
Otherwise, the argument can be relative to the closest star:
"Earth/Moon".
And if the solar system of this star
contains only one
Object
with the given name,
we can just say
"Moon".
The argument can be any of the following.
"Sol/Earth/Moon",
"Sol/Earth/Washington D.C.",
"Solar System Barycenter",
or
"Betelgeuse")("M 31").
"Alpha Orionis",
"Alpha Ori",
"ALF Ori",
or even
std.char.alpha .. " Orionis")"58 Orionis"
or
"58 Ori")"HIP 27989")"HD 39801")"SAO 113271")
Since an
Object
can have more than one name,
the return value of the
name
method of the found
Object
may be different from the argument passed to
find.
See also
Celestia:oldfind,
Object:name,
and
Object:pathname.
Suppose the
Object
cannot be found.
If the Celx Standard Library has not been
required,
find
will return a dummy
Object
whose
name
is
"?"
and whose
type
is
"null".
If the library has been
required,
find
will call the Lua function
error.
To capture the error under a containment dome, call
find
inside the Lua function
pcall.
Print a message in the lower left corner of the window,
five lines up from the bottom.
The message may contain newline characters
(\n),
in which case the first four and a half lines of the message
will appear in the window.
The font and color are the same as
Celestia:print
(celestiaPrint).
The second argument is the number of real-time seconds
that the message will stay in the window,
including a half-second fade-out.
The argument defaults to 1.5,
and is set to 1.5 if it is negative.
See also
Celestia:log.
Convert a
Julian date
to a UTC date and time.
The Julian date is a single number;
the UTC date and time is a table containing the six fields
year,
month,
day,
hour,
minute,
and
seconds.
The first five fields are whole numbers;
the last can have a fraction.
The month numbers range from 1 to 12 inclusive.
A year value of 0 means 1 BC.
The argument of this method must be a Julian date returned by
Celestia:tojulianday,
plus or minus a number of days (possibly with a fraction).
Any other argument will produce meaningless results.
In particular, the argument must not be the return value of
Celestia:gettime
or
Celestia:utctotdb.
Celestia:fromjulianday
follows two simple rules:
year
field is
–4712,
because
Celestia:fromjulianday
is unaware that there was no year 0 A.D.
It’s also unaware that the eleven days from September 3 to 13,
1752 did not exist.)
Celestia:fromjulianday
believes that every day has 24 hours,
every hour has 60 minutes,
and every minute has 60 seconds.
See
leapSeconds
and
stepThrough
for using
Celestia:fromjulianday
and
tojulianday
for stepping through the calendar.
See also
Celestia:tdbtoutc,
Celestia:utctotdb,
and
Phase:timespan.
Return a
boolean
indicating if altazimuth mode is currently in effect.
See also
Celestia:setaltazimuthmode.
Return the ambient light level
in the range 0 (dim) to 1 (bright) inclusive.
The default value of .1
is restored by
Celestia:sane.
See also
Celestia:setambient.
Return the deep sky object
(galaxy, globular cluster, open cluster, or nebula)
with the given id number.
The argument must be a whole number in the range 0 to
celestia:getdsocount() - 1
inclusive;
a fractional part will be ignored.
The deep sky objects are listed in the
DeepSkyCatalogs
in
celestia.cfg.
See also
Celestia:getdsocount
and
Celestia:dsos.
Return the number of deep sky objects
(galaxies, globular clusters, open clusters, and nebulæ)
in the
DeepSkyCatalogs
in
celestia.cfg.
See also
Celestia:getdso
and
Celestia:dsos.
Return the function that was set by
Celestia:registereventhandler
to handle events of the given type,
or
nil
if no function was set.
The possible types are the strings
"key",
"mousedown",
"mouseup",
and
"tick".
Get the apparent magnitude
(loopDatabase)
of the faintest visible stars.
If the
"automag"
renderflag is enabled,
fainter stars automatically become visible as the field of view gets narrower.
In this case,
Celestia:getfaintestvisible
returns the apparent magnitude of the faintest stars visible when the
vertical field of view is
45°.
If
"automag"
is disabled,
the faintest stars visible always have the same apparent magnitude,
and
Celestia:getfaintestvisible
returns this magnitude.
See also
Celestia:setfaintestvisible.
Return the
Font
object specified by the
Font
parameter in
celestia.cfg,
or
fonts/default.txf
if the parameter is missing.
Get the galaxy brightness,
in the range 0 (dim) to 1 (bright) inclusive.
The initial value of .5 is restored by
Celestia:sane.
See also
Celestia:setgalaxylightgain.
Return the red, green, and blue components of the label color for the given
type
of
Object.
The argument must be one of the following case-sensitive strings:
"asteroids",
"comets",
"constellations",
"dwarfplanets",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"galaxies",
"globulars",
"horizontalgrid",
"locations",
"minormoons",
"moons",
"nebulae",
"openclusters",
"planetographicgrid",
"planets",
"spacecraft",
or
"stars".
Note:
"planetographic grid"
has a space in the argument of
Object:addreferencemark.
The return values are in the range 0 to 1 inclusive.
See
version/src/celengine/render.cpp
for the default values.
See also
Celestia:setlabelcolor.
Return a table of
boolean
values indicating the
types
of
Objects
that are labelled.
The keys are the strings
"asteroids",
"constellations",
"comets",
"dwarfplanets",
"galaxies",
"globulars",
"i18nconstellations",
"locations",
"minormoons",
"moons",
"nebulae",
"openclusters",
"planets",
"spacecraft",
"stars".
See also
Celestia:setlabelflags,
Celestia:showlabel,
and
Celestia:hidelabel.
Get the red, green, and blue components of the color of the lines
of the given type.
The argument must be one of the following case-sensitive strings:
"asteroidorbits",
"boundaries",
"cometorbits",
"constellations",
"dwarfplanetorbits",
"ecliptic",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"horizontalgrid",
"minormoonorbits",
"moonorbits",
"planetequator",
"planetographicgrid",
"planetorbits",
"selectioncursor",
"spacecraftorbits",
or
"starorbits".
Note:
"planetographic grid"
has a space in the argument of
Object:addreferencemark.
The return values are in the range 0 to 1 inclusive.
See
version/src/celengine/render.cpp
for the default values.
See also
Celestia:setlinecolor.
Get the minimum apparent radius in pixels that a surface feature would need
in order to merit a label.
Smaller features will not be labelled.
A surface feature is an
Object
of
type
"location".
The feature’s radius in kilometers is assumed to be equal to its
Importance
in its
.ssc
file.
If it has no
Importance,
its radius is assumed to be half of its
Size
in kilometers.
The default minimum feature size is 20 pixels,
restored by
Celestia:sane.
See the substantial example in
Celestia:setminfeaturesize
for the rôle played by the feature’s level of
Importance.
Get the minimum apparent radius in pixels that an orbit would need
in order to be rendered.
Smaller orbits will not be drawn.
The radius of the orbit is measured at its apoapsis.
The default minimum apparent radius is 20 pixels,
restored by
Celestia:sane.
See also
Celestia:getorbitflags,
Celestia:setminorbitsize,
and
Object:setorbitvisibility.
Return the
Observer
that belongs to the active view.
If there is only one view,
it is the active one.
This method cannot be called
during the execution of a file that creates a Lua hook
(luaHookFunctions),
scripted orbit
(scriptedOrbit),
or scripted rotation
(scriptedRotation).
That’s why we can’t
require("std")
at the top of these files.
It can be called later, however,
during the execution of the methods created in these files.
See also
Celestia:getobservers
and
Celestia:sane.
Return an array of all the
Observers.
See
Splitview.
The aray initially contains one
Observer.
A new
Observer
is created and appended to the array by
Observer:splitview.
An
Observer
is deleted from the array by
Observer:deleteview.
The array is empty during the execution of a file that creates a Lua hook
(luaHookFunctions),
scripted orbit
(scriptedOrbit),
or scripted rotation
(scriptedRotation).
That’s why we can’t
require("std")
at the top of these files.
At all other times the array is never empty,
because the last
Observer
cannot be deleted.
In particular,
the array is nonempty
during the execution of the methods created in these files.
See also
Celestia:getobserver.
Return a table of
boolean
values giving the types of
Objects
whose orbits are rendered.
The keys are the strings
"Asteroid",
"Comet",
"DwarfPlanet",
"Invisible",
"MinorMoon",
"Moon",
"Planet",
"Spacecraft",
"Star",
and
"Unknown".
See
Object:setorbitvisibility
for the complicated interactions between the renderflags and the orbitflags.
See also
Celestia:getminorbitsize
and
Celestia:setorbitflags.
Return a table of
boolean
values giving the items displayed in the transparent overlay atop the
Celestia window.
The keys are the strings
"Frame",
"Selection",
"Time",
and
"Velocity".
See also
Celestia:setoverlayelements.
Return the value of a string parameter in the
celestia.cfg
file.
The argument is case-sensitive.
The null string
""
is returned if the parameter is not found,
or if the parameter’s value is a number or list.
Return a table of
boolean
values indicating what things will be rendered.
They may be the following case-sensitive strings:
"atmospheres",
"automag",
"boundaries",
"cloudmaps",
"cloudshadows",
"comettails",
"constellations",
"eclipseshadows",
"ecliptic",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"galaxies",
"globulars",
"grid",
"horizontalgrid",
"lightdelay",
"markers",
"nebulae",
"nightmaps",
"openclusters",
"orbits",
"partialtrajectories",
"planets",
"ringshadows",
and
"smoothlines".
See
renderFlags
for an example.
See also
Celestia:setrenderflags,
Celestia:show
and
Celestia:hide.
Return the width and height in pixels of the Celestia window,
not counting the title and scrollbars provided by the operating system.
The return values are whole numbers taken from the OpenGL viewport,
and are suitable for passing to
glu.Ortho2D.
There is no
Celestia:setscreendimension
method,
but the
"resize"
Lua hook will be called when the window is resized.
See
luaHookFunctions
and
Celestia:setluahook.
Warning:
Celestia:getscreendimension
returns the wrong width and height between calls to
gl.Begin
and
gl.End.
See
traceRetrograde.
See also
Observer:getfov
and the other
“field of view” functions;
and
Observer:getscreencoordinates.
Return the name of the Celx file that contains the call to
Celestia:getscriptpath.
If the file is a plain old Celx program specified as a command line argument
to Celestia,
the return value is this argument.
If the file is a Lua hook file
(luaHookFunctions),
the return value is the argument of the
LuaHook
parameter in
celestia.cfg.
If the file is a scripted orbit or a scripted rotation file
(scriptedOrbit),
the return value is
nil.
When a Celx program is run by typing its name as a command line
in Microsoft Windows,
the return value of
Celestia:getscriptpath
is the full pathname of the program.
(This is a feature of the
ftype %1
in the Command Prompt window;
see
windowsCelestia.)
Otherwise,
no additional directory names is appended
to the filename in the previous paragraph.
See also
Celestia:loadtexture
and
Celestia:runscript.
Return the number of real-time seconds
since the Celx program started running.
Unlike the simulation time returned by
Celestia:gettime,
the script time can advance even if the
wait
function has not been called.
For the current real time,
call
Celestia:getsystemtime
or the Lua function
os.date.
See also
Celestia:getsystemtime,
Celestia:settimeslice,
and the Lua function
os.difftime.
Return the currently selected
Object.
If no
Object
is selected, return a dummy
Object
with name
name
"?"
and
type
"null".
See also
Celestia:select.
Return the star with the given id number in the
StarDatabase
and
StarCatalogs
in
celestia.cfg.
The “star” may be a true star,
stellar system barycenter, neutron star, or black hole.
The argument must be a whole number in the range 0 to
Celestia:getstarcount() - 1
inclusive.
See also
Celestia:getstarcount,
Celestia:getstar,
and
Object:spectraltype.
Return the number of stars in the
StarDatabase
and
StarCatalogs
in
celestia.cfg.
The “star” may be a true star,
stellar system barycenter, neutron star, or black hole.
See also
Celestia:getstar
and
Celestia:stars.
Return the star distance limit in lightyears.
Stars farther than this distance from the
Observer
will not be rendered.
The default value of one million lightyears
(20 times the radius of the
Milky Way)
is restored by
Celestia:sane.
See also
Celestia:setstardistancelimit.
Return the star style:
"fuzzy" (the default),
"point",
or
"disc".
See also
Celestia:setstarstyle.
Return the current real time in UTC,
updated only once per second.
By default,
the real time is the same as the simulation time,
but the latter flows more smoothly
(Exponential).
See also
Celestia:getscripttime
and
Celestia:gettime.
Return red, green, and blue components of the color of the text printed by
Celestia:print
and
Celestia:log.
See
celestiaPrint.
Each value is a whole number in the range 0 to 255,
divided by 255.
The alpha level is 1.
See also
Celestia:settextcolor.
Return the texture resolution:
0 for low resolution,
1 for medium,
or 2 for high.
The resolution determines whether the texture files are read from the
lores,
medres,
or
hires
subdirectories of the
textures
subdirectory of the Celx directory.
See also
Celestia:settextureresolution.
Return the width in pixels of the string argument.
The return value is a whole number;
see
Iapetus
for an example.
The font is that used by
Celestia:print
and
Celestia:log.
For the width in other fonts, call
Font:getwidth.
See also
Celestia:getscreendimension.
Return the current simulation time of the active
Observer.
For the simulation time of the other
Observers,
call
Observer:gettime
if their times are not synchronized.
See
Celestia:istimesynchronized.
By default, the simulation time of the active
Observer
is the same as the real time returned by
Celestia:getsystemtime,
but the former runs more smoothly.
See
Exponential.
The return value of
Celestia:gettime
can be passed to
Celestia:tdbtoutc
but not to
Celestia:fromjulianday;
see
tdb.
See also
Celestia:settime
and
Celestia:gettimescale.
Get the speed at which the simulation time passes for all
Observers.
See
settime.
The return value is in units of simulation time per unit of real time.
It can be positive, negative, or zero;
the default value of 1 is restored by
Celestia:sane.
Pressing the space bar to pause the Celx program
has no effect on the timescale.
Return the
Font
used by
Celestia:print
and
Celestia:flash.
See
celestiaPrint.
The font is set by the
TitleFont
parameter in
celestia.cfg,
which defaults to the
Font
parameter,
which defaults to
fonts/default.txf.
Return a
URL
that contains the state of an
Observer.
The argument defaults to the active
Observer;
the return value is a string that can be pasted into a web browser.
The corresponding keystroke command is
command-c on Macintosh,
control-c on Microsoft Windows.
The “frame of reference” field of the URL
does not know about the equatorial frame
(equatorialFrame)
and renders it as
Unknown.
The
track
and
select
fields are optional.
They could have been captured very easily if a Lua
pattern
permitted us to apply the “optional” operator
?
to an expression that is bigger than one wildcard.
The workaround is to use
if
statements.
The
x,
y,
z
fields of the
Observer’s
position are measured with respect to the frame of reference
to which he has been
setframed,
and are encoded in the format described in
bits128.
The light time delay and paused fields are
1
or
0.
The renderflags and label mode are integers whose bits correspond
to the enumeration values in
version/src/celengine/render.h.
The URL version is 3 in Celestia 1.6.1; earlier Celestias generated a URL with no version number at all. The URL version number is important because the origin of the universal frame was in a different place in earlier versions of Celestia.
The time source field is used when the URL is passed to
Celestia:seturl.
Its value is one of the
TimeSource
enumerations in
version/src/celengine/render.h.
For example,
0 sets the simulation time to the time stored in the URL,
and 1 leaves the simulation time unchanged.
See also
Celestia:newposition
and
std.tourl.
--[[
Parse a cel: URL.
]]
require("std")
local function main()
local observer = celestia:sane()
observer:setposition(std.position0)
local url = celestia:geturl(observer)
--optional fields
local trackPattern = "()" --capture no characters
if url:find("&track=") then
trackPattern = "&track=([^&]+)"
end
local selectPattern = "()"
if url:find("&select=") then
selectPattern = "&select=([^&]+)"
end
local pattern =
"^(cel):"
.. "//(.+)" --frame of reference
.. "/([-]?%d+-%d+-%d+)" --date
.. "T([^?]+)" --time
.. "%?x=([^&]*)" --observer position
.. "&y=([^&]*)"
.. "&z=([^&]*)"
.. "&ow=([^&]*)" --observer orientation:
.. "&ox=([^&]*)" --w is the real part;
.. "&oy=([^&]*)" --(x, y, z) is the imaginary.
.. "&oz=([^&]*)"
.. trackPattern --tracked object
.. selectPattern --selected object
.. "&fov=([^&]*)" --field of view, in degrees
.. "&ts=([^&]*)" --time scale
.. "<d=([^&]*)" --light time delay
.. "&p=([^&]*)" --paused
.. "&rf=([^&]*)" --renderflags
.. "&lm=([^&]*)" --label mode
.. "&tsrc=([^&]*)" --time source
.. "&ver=([^&]*)" --version
local index1, index2, protocol, frame,
date, time,
x, y, z,
ow, ox, oy, oz,
track, select,
fov, ts, ltd, p, rf, lm, tsrc, ver = url:find(pattern)
local position = celestia:newposition(x, y, z)
local decimal = position:getdecimal()
if trackPattern == "()" then
track = ""
end
if selectPattern == "()" then
select = ""
end
local len = url:len()
if len % 2 == 1 then --If len is odd,
len = len - 1 --make it even.
end
local s = string.format(
"%s\n"
.. "%s\n\n"
.. "protocol %s\n"
.. "frame of reference %s\n"
.. "date %s\n"
.. "time %s\n"
.. "position (%s, %s, %s)\n"
.. "orientation wxyz (%s, %s, %s, %s)\n"
.. "track %s\n"
.. "select %s\n"
.. "field of view %g%s\n"
.. "time scale %d\n"
.. "light time delay %d\n"
.. "paused %d\n"
.. "renderflags %X\n" --hexadecimal
.. "label mode %X\n"
.. "time source %d\n"
.. "version %d",
url:sub(1, len / 2), url:sub(len / 2 + 1),
protocol, frame, date, time,
position.x, position.y, position.z,
ow, ox, oy, oz,
track, select,
fov, std.char.degree,
ts, ltd, p, rf, lm, tsrc, ver)
celestia:print(s, math.huge, -1, 1, 1, -1)
wait()
end
main()
cel://Freeflight/2013-03-07T18:24:10.18550?x=&y=&z=&ow=1&ox=0&oy=0
&oz=0&fov=32.9778&ts=1<d=0&p=0&rf=37738463&lm=22303&tsrc=0&ver=3
protocol cel
frame of reference Freeflight
date 2013-03-07
time 18:24:10.18550
position (0, 0, 0)
orientation wxyz (1, 0, 0, 0)
track
select
field of view 32.9778°
time scale 1
light time delay 0
paused 0
renderflags 23FD7DF
label mode 571F
time source 0
version 3
Turn off the given renderflags
(renderFlags).
Do not call this method before
Celestia:sane,
since the latter sets the flags back to ther default values.
Celestia:hide
accepts a variable number of
the following case-sensitive strings:
"atmospheres",
"automag",
"boundaries",
"cloudmaps",
"cloudshadows",
"comettails",
"constellations",
"eclipseshadows",
"ecliptic",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"galaxies",
"globulars",
"grid",
"horizontalgrid",
"lightdelay",
"markers",
"nebulae",
"nightmaps",
"openclusters",
"orbits",
"partialtrajectories",
"planets",
"ringshadows",
and
"smoothlines".
Hiding the constellations does not hide their names;
use
Celestia:hidelabel.
See also
Celestia:show,
Celestia:getrenderflags,
and
Celestia:setrenderflags.
Hide the names and stick figures of the specified constellations.
The optional argument is an array of case-insensitive constellation names
from the
AsterismFile
in
celestia.cfg.
With no argument,
all the constellations are hidden.
Celestia:sane
shows all the constellations.
See also
Celestia:showconstellations,
Celestia:hide,
and
Celestia:hidelabel.
Hide the labels on the constellations and/or the celestial
Objects
of the given types.
Do not call this method before
Celestia:sane,
since the latter sets the flags back to their default values.
Celestia:hidelabel
accepts a variable number of
the following case-sensitive strings:
"asteroids",
"constellations",
"comets",
"dwarfplanets",
"galaxies",
"globulars",
"i18nconstellations",
"locations",
"minormoons",
"moons",
"nebulae",
"openclusters",
"planets",
"spacecraft",
"stars".
If the labels for
"i18nconstellations"
are hidden,
the constellation names will be in Latin.
If the labels for
"constellations"
are also hidden,
the constellation names will be hidden.
See also
Celestia:showlabel,
Celestia:getlabelflags,
Celestia:setlabelflags,
and
Celestia:hideconstellations.
Return
true
if this Celx program is currently paused.
A program may be paused and unpaused by pressing the space bar.
Event handlers
(eventHandler)
and Lua hooks
(luaHookFunctions)
can be called while the program is paused,
but no other statements will be executed.
Therefore it makes sense to call
Celestia:ispaused
only in those functions.
The simulation time will remain frozen while the program is paused,
but, paradoxically, the return value of
Celestia:gettimescale
will not be affected.
Return
true
if all of the
Observers
have the same simulation time.
If so, a call to
Celestia:settime
will set the simulation time for every
Observer.
Otherwise, it will set the simulation time for only the active
Observer.
See also
Celestia:synchronizetime.
Return a
Font
object for the
.txf
font file with the given name.
The name is relative to the Celx directory,
and is case-insensitive only on Macintosh.
See the
Celestia:print
example in
celestiaPrint
and the OpenGL example in
opengl.
Return a
Texture
object for the image file with the given name.
The name is case-insensitive only on Macintosh,
and is relative to the directory that contains the Celx file that called
loadtexture.
This Celx file must be specified with a name that contains a slash.
In Unix, for example, the command line argument of Celestia that
specifies the Celx file would have to be
./myprog.celx
or
/pathname/of/myprog.celx
instead of plain old
myprog.celx.
See the OpenGL example in
opengl.
Append the given string and a newline to the text in the Celestia console.
See
console.
The console retains only the last 200 lines of text,
overridden by the
LogSize
in
celestia.cfg.
(Actually, it’s just 199.)
A line longer than 120 characters will be split,
counting as two separate lines for the 199-line limit.
Press
~
(tilde) to toggle the console visibility,
the up and down arrows to scroll it,
and
Page Up
and
Page Down
to scroll 10 lines at a time.
The color is white, with alpha level 1.
The font is the
Font
parameter in
celestia.cfg,
defaulting to
fonts/default.txf.
See also
Celestia:flash
and
Celestia:print.
Mark a celestial
Object
with a green diamond of diameter 10 pixels
and an alpha level of 1.
Call
Object:mark
to get control over these parameters.
An
Object
can have only one mark at a time;
a second call to
mark
will be ignored unless the
Object
is first
unmarked.
The corresponding keystroke command is
control-p.
See also
Celestia:unmark,
Celestia:unmarkall,
and
Object:unmark.
Mark the center of the window with the string
"MM".
The center of the window is the direction of the
Observer’s
view, i.e., his forward vector.
The exact center of the window lies between the two letters at their baseline.
See
celestiaPrint
and the
tick handler examples in
celestialDome
and
j2000Equatorial.
The first argument is a string to be printed below the
"MM",
defaulting to the empty string
"".
The second argument is the number of real-time seconds
during which the text is displayed,
defaulting to
math.huge.
Create and return a new
Frame
object representing a frame of reference
(framesOfReference).
The first argument specifies the
Frame’s
coördinate system as
a case-sensitive string:
"universal",
"ecliptic",
"equatorial",
"bodyfixed",
"chase",
or
"lock".
See
namesOfFrames.
If the coördinate system is not universal,
the second argument is the reference
Object
of the
Frame.
If the coördinate system is lock,
the third argument is the target
Object
of the
Frame.
The target and reference
Objects
can not be the same
Object.
If the Celx Standard Library has been included with
require("std"),
an optional last argument of
Celestia:newframe
can specify a
Rotation.
This causes the method
to return a rotated frame instead of a plain old
Frame.
The rotated frame has the same origin as the plain old
Frame,
but is rotated therefrom by the specified
Rotation.
See
rotatedRadec.
See also
Frame:getcoordinatesystem
and
Observer:setframe.
Create and return a new
Position
object containing the specified
x,
y,
z
coördinates in microlightyears.
Each argument can be a Celx number,
which is a double precision floating point number
and thus probably limited to 15 significant digits
(doubleArithmetic).
Each argument can also be a string that encodes a 128-bit fixed-point number,
which can hold a much higher precision
(positionCoordinates).
See
bits128
for the encoding.
See
Position:getdecimal
to render the coördinates as humanly-readable strings.
See also
Celestia:newpositionaltaz,
Celestia:newpositionlonglat,
Celestia:newpositionradec,
and
std.tourl.
Create and return a new
Position
object whose spherical coördinates are the specified altitude and azimuth
in radians.
See
celestialDome
for the altazimuth coördinate system.
The altitude is measured up or down from the XZ plane; its absolute value must be less than or equal to π/2. The azimuth is measured clockwise in the XZ plane from the negative Z axis; its absolute value must be less than 2π. This X axis points east, the Z axis points south, and the Y axis points up. The distance from the origin, in microlightyears, must be nonnegative and defaults to 1.
See also
Celestia:newposition,
Celestia:newpositionlonglat,
Celestia:newpositionradec,
and
Position:getaltaz.
Create a return a
Position
object with the given spherical coördinates in radians.
The longitude
is measured counterclockwise in the XZ plane from the positive X axis;
its absolute value must be less than
2π.
The latitude is measured above or below the XZ plane;
its absolute value must be less than or equal to
π/2.
The longitude argument comes before the latitude to agree with
Observer:gotolonglat.
The distance from the origin, in microlightyears,
must be nonnegative and defaults to 1.
See also
Celestia:newposition,
Celestia:newpositionaltaz,
and
Celestia:newpositionradec.
Create and return a new
Position
object whose spherical coördinates
are the specified right ascension and declination in radians.
See
j2000Equatorial
for the equatorial coördinate system.
The right ascension is measured counterclockwise in the XZ plane
from the positive X axis;
its absolute value must be less than
2π.
The declination is measured up or down from the XZ plane;
its absolute value must be less than or equal to
π/2.
This X axis points towards the vernal equinox in
Pisces,
and the Y axis points towards the
north celestial pole
near
Polaris.
The distance from the origin, in microlightyears,
must be nonnegative and defaults to 1.
See also
Celestia:newposition.
The two-argument version of this method
creates and returns the
Rotation
with the given axis and angle.
The axis is a unit vector in universal coördinates;
the angle is in radians.
If the angle is negative,
it and the axis will be negated.
The four-argument version creates and returns the
Rotation
with the given coördinates,
if the sum of the squares of the coördinates is 1.
If the sum is not 1, the return value will still belong to class
Rotation
but it will not be a
unit
quaternion.
See also
Rotation:real,
Rotation:imag,
Rotation:getforwardup,
and
Celestia:newrotationforwardup.
Create and return the
Rotation
passed as the third argument of
Celestia:newframe
when creating a
Frame
of reference whose XZ plane is parallel to the horizon at the point
on the surface with the given latitude and longitude.
The X axis of the resulting
Frame
points east,
the Z axis points south,
and the Y axis points up.
The first argument of
Celestia:newframe
must be
"bodyfixed".
Note:
the origin of the
Frame
is the center of the reference object,
not the given point on the surface.
If the point is the north pole, the resulting rotation is almost the same as if the point were latitude 89° N longitude 0° E. The X axis points along the meridian of 90° E and the Z axis along the meridian of 0° E. If the point is the south pole, the resulting rotation is almost the same as if the point were latitude 89° S longitude 0° E. The X axis points along the meridian of 90° E and the –Z axis along the meridian of 0° E.
local earth = celestia:find("Sol/Earth") local latitude = math.rad( 40 + (39 + 51 / 60) / 60 ) --New York City local longitude = math.rad(-(73 + (56 + 19 / 60) / 60)) --west negative local rotation = celestia:newrotationaltaz(longitude, latitude) local frame = celestia:newframe("bodyfixed", earth, rotation) observer:setframe(frame) --On the ground in New York City, 10 meters above sea level to avoid jitter. local microlightyears = (earth:radius() + .01) / KM_PER_MICROLY local position = celestia:newposition(0, microlightyears, 0) observer:setposition(frame:from(position)) --Face east. local forward = celestia:newvectoraltaz(math.deg( 0), math.deg(90), 1) local up = celestia:newvectoraltaz(math.deg(90), math.deg( 0), 1) local orientation = celestia:newrotationforwardup(forward, up) observer:setorientation(frame:from(orientation))
Create and return the orientation (i.e., the
Rotation)
with the given forward and up
Vectors.
The arguments are non-colinear
Vectors
in the universal
Frame.
They do not have to be unit
Vectors,
but they must be nonzero.
To convert the
Rotation
back into its
forward and up
Vectors,
call
Rotation:getforwardup.
Create and return a new
Vector
with the given
x,
y,
z
coördinates in microlightyears.
To create a
Vector
from spherical coördinates,
see
Celestia:newvectoraltaz
or
Celestia:newvectorlonglat.
To retrieve the
x,
y,
z
coördinates of a
Vector,
see the
getx,
gety,
getz,
and
getxyz
members of class
Vector.
Create and return a new
Vector
whose spherical coördinates
are the specified altitude and azimuth in radians.
See
celestialDome
for the altazimuth coördinate system.
The altitude is measured up or down from the XZ plane; its absolute value must be less than or equal to π/2. The azimuth is measured clockwise in the XZ plane from the negative Z axis; its absolute value must be less than 2π. This X axis points east, the Z axis points south, and the Y axis points up. The distance from the origin, in microlightyears, must be nonnegative and defaults to 1.
See also
Celestia:newvector,
Celestia:newvectorlonglat,
and
Celestia:newvectorradec.
Create and return a
Vector
with the given spherical coördinates in radians.
The longitude is measured counterclockwise in the XZ plane
from the positive X axis;
its absolute value must be less than
2π.
The latitude is measured up or down form the XZ plane;
its absolute value must be less than or equal to
π/2.
The longitude argument comes before the latitude to agree with
Observer:gotolonglat.
The distance from the origin,
in microlightyears, must be nonnegative and defaults to 1.
To convert a
Vector
back to its spherical coördinates, see
Vector:getlonglat.
To create a
Vector
from Cartesian
x,
y,
z
coördinates, see
Celestia:newvector.
Create and return a
Vector
whose spherical coördinates
are the given right ascension and declination in radians.
See
j2000Equatorial
for the equatorial coördinate system.
The right ascension is measured counterclockwise in the XZ plane
from the positive X axis;
its absolute value must be less than
2π.
The declination is measured up or down from the XZ plane;
its absolute value must be less than or equal to
π/2.
This X axis points towards the vernal equinox in
Pisces,
and the Y axis points towards the
north celestial pole
near
Polaris.
The distance from the origin, in microlightyears,
must be nonnegative and defaults to 1.
See also
Celestia:newvector.
Return the celestial
Object
with the given name (case-insensitive).
If the search is successful,
Celestia:oldfind
behaves just like
Celestia:find.
Otherwise
Celestia:oldfind
returns a dummy object whose name is
"?"
and whose type is
"null".
Print a message on the transparent OpenGL overlay atop the Celestia window.
See
celestiaPrint.
The first argument is the message.
It can contain the newline character
"\n"
for multiple lines, but none of the other C-like backslash escapes.
(See
Overlay::print
in
versionsrc/celengine/overlay.cpp).
A message longer than
210 – 1
= 1023
characters will not be printed.
The second argument is the duration in seconds of real time
during which the message remains visible,
including a half-second fadeout.
The argument defaults 1.5 seconds.
A negative number is treated as 1.5;
the special value
math.huge
is treated as infinity.
The fractional parts of the last four arguments are ignored. The third and fourth arguments specify the origin from which the fifth and sixth arguments are measured. The third argument is –1 for the left edge of the window, 0 for the center, and 1 for the right edge. The fourth argument is –1 for the bottom edge, 0 for the center, and 1 for the top edge. The third and fourth arguments default to –1, –1, indicating the lower left corner of the window.
The fifth and sixth arguments are the horizontal and vertical offsets
from the origin of the point where the text begins.
The horizontal offset is measured in ems (the width of an uppercase letter M).
The vertical offset is measured in lines of text.
For fractional offsets,
see the
Font:render
examples in
opengl.
and
Sundial.
The fifth and sixth arguments default to 0 and 5 respectively.
The
Font
is set by the
TitleFont
parameter in
celestia.cfg.
It defaults to the
Font
parameter in the same file,
which defaults to
fonts/default.txf.
See
Celestia:gettitlefont.
To print in a different
Font,
use
Font:render.
The color is set by
Celestia:settextcolor
and defaults to white;
see also
Celestia:gettextcolor.
The alpha level is 1.
For a different alpha, call
Font:render.
The angle of the text is horizontal.
For a different pitch, call
glu.lookat.
See also
Celestia:flash,
Celestia:gettextwidth,
and
Celestia:log.
Designate the handler function to be called when an event happens.
The first argument is the type of event:
"key",
"tick",
"mousedown",
or
"mouseup".
The second argument is the function,
or
nil
to ensure that no function is called.
Celestia:sane
sets the handlers for all four events to
nil.
See the examples in
eventHandler.
See also
Celestia:geteventhandler
and
Celestia:setluahook.
With the argument
true,
the nonlocal function
celestia_keyboard_callback
will be called with each keystroke,
if there is a function with that name.
See the complete example in
callback.
Get permission for the Celx program to mention the Lua tables
io
and
os.
These tables contain the functions that talk to the operating system
and its file system.
To access them, the
ScriptSystemAccessPolicy
in
celestia.cfg
must be
"ask"
or
"allow"
(case insensitive).
See
osExit.
If the policy is
"ask",
Celestia:requestsystemaccess
prints the following message.
If the policy is
"ask",
Celestia:requestsystemaccess
must be followed by a call to
wait.
The
wait
is not necessary for other policies.
If permission is denied,
io
and
os
will be
nil.
Run a Celx or Cel program that resides in a separate file.
Celestia uses the filename extension
to identify the language:
.cel
for Cel,
.celx
or
.clx
for Celx.
If successful, this method never returns.
The filename is case-insensitive only on Macintosh,
and is relative to the directory that contains the Celx file that called
Celestia:runscript.
This Celx file must be specified with a name that contains a slash
(or backslash in Windows).
In Unix, for example,
the command line argument of Celestia
that specifies the Celx file would have to be
./myprog.celx
or
/pathname/of/myprog.celx
instead of plain old
myprog.celx.
See also
Celestia:createcelscript
and
Celscript:tick.
Set Celestia’s options to sane values,
usually their initial or default settings.
These options include the renderflags, orbitflags, labelflags,
overlayelements,
label colors, line colors,
location flags,
and the values set and get by the methods of the
Celestia
object.
For details, see the source code of the
Celestia:sane
function in the Celx Standard Library file
std.lua
in
stdCelx.
Celestia:sane
is usually called in the first line of the
main
function of a Celx program
in order to reset any settings left over
from the previous Celx program run by the same instance of Celestia.
It deletes the non-active
Observers
and returns the active one.
Select the given celestial
Object.
To unselect the object,
pass the argument
nil.
See the effect of selection in
Object:setorbitvisibility.
The corresponding keystroke command is
h
(for the Sun).
See also
Celestia:getselection
and the
"Selection"
flag in
Celestia:getoverlayelements
and the
"selectioncursor"
in
Celestia:setlinecolor.
Turn altazimuth mode on or off with the boolean argument.
In this mode, the left and right arrow keys will yaw the
Observer
instead of rotating him.
An example is in
celestialDome.
The initial value of
false
is restored by
Celestia:sane.
The corresponding keystroke command is
control-f.
See also
Celestia:getaltazimuthmode.
Set the level of ambient white light.
The argument is clamped to the range 0 (dim) to 1 (bright) inclusive,
and the initial value of .1 is restored by
Celestia:sane.
The corresponding keystroke commands are
{
(dimmer)
and
}
(brighter).
See also
Celestia:getambient.
Set the color of the given constellation(s).
The first three arguments are the red, green, and blue components of the color,
in the range 0 to 1 inclusive.
The alpha level is 1.
The optional fourth argument is an array of case-insensitive constellation names
from the
AsterismsFile
in
celestia.cfg.
With no fourth argument,
all of the constellations will be set.
This method overrides a color set by
Celestia:setlinecolor.
Once a color has been set,
it can be set to another color but not unset.
The closest we can get to unsetting is to
change it back to the initial color of
(.0, .24, .36),
which comes from
version/src/celengine/render.cpp.
By default, the
AsterismsFile
is
data/asterisms.dat.
The names in this file are different from those in
std.constellations
(taken from
version/src/celengine/constellation.cpp).
The former has
"Serpens Caput"
and
"Serpens Cauda";
the latter has
"Serpens".
Set the magnitude of the faintest stars visible. Dimmer stars (i.e., those with higher magnitude numbers) will not be seen.
If the
"automag"
renderflag is enabled,
fainter stars will automatically become visible
as the field of view gets narrower.
In this case the argument is clamped to the range 6 to 12 inclusive,
and
Celestia:setfaintestvisible
sets the apparent magnitude of the faintest stars visible when the
vertical field of view is
45°.
If
"automag"
is disabled,
the argument is clamped to the range 1 to 15 inclusive and
Celestia:getfaintestvisible
sets the magnitude of the faintest stars visible.
The initial values
(7 with
"automag"
on,
5 with
"automag"
off)
are restored by
Celestia:sane.
The corresponding keystroke commands are
[
and
].
The
[
increases the magnitude number,
so fewer stars are visible.
See also
Celestia:getfaintestvisible.
Set the galaxy brightness.
The argument is clamped to the range 0 (dim) to 1 (bright).
The initial value of .5 is restored by
Celestia:sane.
The corresponding keystroke commands are
(
(dimmer)
and
)
(brighter).
See also
Celestia:getgalaxylightgain.
Set the label color for
Objects
of the given
type.
The first argument must be one of the following case-sensitive strings:
"asteroids",
"comets",
"constellations",
"dwarfplanets",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"galaxies",
"globulars",
"horizontalgrid",
"locations",
"minormoons",
"moons",
"nebulae",
"openclusters",
"planetographicgrid",
"planets",
"spacecraft",
or
"stars".
Note:
"planetographic grid"
has a space in the argument of
Object:addreferencemark.
The last three arguments are the red, green, and blue components of the color,
in the range 0 to 1 inclusive.
The alpha level is 1.
The initial values
(taken from
version/src/celengine/render.cpp)
are restored by
Celestia:sane.
See also
Celestia:getlabelcolor.
Set which things will be labelled.
The argument is a table of
boolean
values whose keys are the strings
"asteroids",
"constellations",
"comets",
"dwarfplanets",
"galaxies",
"globulars",
"i18nconstellations",
"locations",
"minormoons",
"moons",
"nebulae",
"openclusters",
"planets",
"spacecraft",
"stars".
A missing field has no effect on the existing labelflags.
Celestia:sane
sets the flags to sane values.
The
"nightmaps"
of city lights are displayed even for dates before the invention of
electric lights.
See also
Celestia:getlabelflags,
Celestia:showlabel,
Celestia:hidelabel,
Celestia:setlabelcolor,
Celestia:showconstellations.
Set the color in which lines will be drawn.
The first argument must be one of the following case-sensitive strings:
"asteroidorbits",
"boundaries",
"cometorbits",
"constellations",
"dwarfplanetorbits",
"ecliptic",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"horizontalgrid",
"minormoonorbits",
"moonorbits",
"planetequator",
"planetographicgrid",
"planetorbits",
"selectioncursor",
"spacecraftorbits",
or
"starorbits".
Note:
"planetographic grid"
has a space in the argument of
Object:addreferencemark.
The next three arguments are the red, green, and blue components,
in the range 0 to 1 inclusive.
The alpha level is 1.
The initial values
(taken from
version/src/celengine/render.cpp)
are restored by
Celestia:sane.
A constellation color set by
Celestia:setlinecolor
is overridden by
Celestia:setconstellationcolor.
See also
Celestia:getlinecolor.
Designate the methods to be called when certain events happen.
Celestia:setluahook
is called in the file specified by the
LuaHook
parameter in
celestia.cfg.
Its argument is a table of methods.
See
luaHookFunctions.
The keys of the table may include the strings
"charentered",
"keydown",
"mousebuttondown",
"mousebuttonmove",
"mousebuttonup",
"mousemove",
"renderoverlay",
"resize",
and
"tick".
The values corresponding to the keys are methods,
i.e., functions whose first argument is
self.
The
self
refers to the table itself,
allowing each method to access other fields in the table such as the
resizeString
below.
For the additional arguments of each function,
and the return value of each function,
see the big example in
luaHookFunctions.
The Celestia Standard Library can not be
required
when the
luahook.celx
file is executed.
If needed, it must be
required
later, when the methods in the table are called.
See also the Lua function
debug.sethook.
--This file is luahook.celx.
local hooks = {
resizeString = "Resize window by dragging on lower left corner.",
renderoverlay = function(self)
celestia:print(self.resizeString, 1, -1, -1, 1, 5)
end,
resize = function(self, width, height)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
end
self.resizeString =
string.format("%d %s %d", width, std.char.times, height)
end
}
celestia:setluahook(hooks)
Set the minimum apparent radius in pixels that a surface feature
would need in order to merit a label.
Smaller features will not be labelled.
A surface feature is an
Object
of
type
"location".
For purposes of labelling merit,
a feature’s radius in kilometers is assumed to be equal to its
Importance
in its
.ssc
file.
If it has no
Importance,
its radius is assumed to be half of its
Size
in kilometers.
A negative argument is treated as zero pixels,
causing every feature to be labelled.
The initial minimum feature size of 20 pixels is restored by
Celestia:sane.
See also
Celestia:getminfeaturesize.
--[[
Position the observer directly above Mare Imbrium, 5 lunar radii from the center
of the Moon. Mare Imbrium is circular (it has a radius) because it is an impact
feature, the largest known on the Moon when the author was a boy. Set the
minfeaturesize barely small enough to label Mare Imbrium from this vantage
point. As soon as you zoom out by pressing one dot, the label disappears.
Zooom back in with one comma to make the label reappear.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local imbrium = celestia:find("Sol/Earth/Moon/Mare Imbrium") --one space
local radiusInKilometers = imbrium:getinfo().importance
if radiusInKilometers < 0 then --no Importance in .ssc file
radiusInKilometers = imbrium:radius()
end
--[[
Return the user's distance in pixels from the center of the window,
i.e., the number of pixels he or she would have to be away from the window
in order to make it subtend the given vertical field of view.
]]
local function userDistance()
local width, height = celestia:getscreendimension()
local tangent = math.tan(observer:getfov() / 2)
assert(tangent > 0)
return (height / 2) / tangent
end
local function tickHandler()
local distanceInKilometers =
observer:getposition():distanceto(imbrium:getposition())
local angularRadius =
math.atan2(radiusInKilometers, distanceInKilometers)
local distanceInPixels = userDistance()
local radiusInPixels = distanceInPixels * math.tan(angularRadius)
local s = string.format(
"Simulated space, in kilometers:\n"
.. "Observer's distance from Moon = %.15g\n"
.. "Mare Imbrium's radius = %.15g\n"
.. "angular radius = %.15g%s\n\n"
.. "Real space, in pixels:\n"
.. "User's distance from window = %.15g\n"
.. "Mare Imbrium's radius = %.15g pixels\n"
.. "minfeaturesize = %.15g pixels",
distanceInKilometers,
radiusInKilometers,
math.deg(angularRadius), std.char.degree,
distanceInPixels,
radiusInPixels,
celestia:getminfeaturesize())
celestia:print(s, 1, -1, -1, 1, 10)
end
local function main()
celestia:setambient(.5) --so we can see the Mare even during lunar night
celestia:select(imbrium)
--The "Moon" label interferes with the "MARE IMBRIUM" label.
celestia:hidelabel("moons")
celestia:showlabel("locations")
local moon = celestia:find("Sol/Earth/Moon")
local bodyfixedFrame = celestia:newframe("bodyfixed", moon)
observer:setframe(bodyfixedFrame)
local imbriumPosition = bodyfixedFrame:to(imbrium:getposition())
local observerPosition = 5 * imbriumPosition
local distanceInKilometers =
observerPosition:distanceto(imbriumPosition)
local angularRadius =
math.atan2(radiusInKilometers, distanceInKilometers)
local radiusInPixels = userDistance() * math.tan(angularRadius)
celestia:setminfeaturesize(.999 * radiusInPixels)
observer:setposition(bodyfixedFrame:from(observerPosition))
observer:lookat(
bodyfixedFrame:from(std.position0),
bodyfixedFrame:from(std.yaxis))
celestia:registereventhandler("tick", tickHandler)
wait()
end
main()
Simulated space, in kilometers:
Observer's distance from Moon = 6950.11994172442
Mare Imbrium's radius = 56.2700004577637
angular radius = 0.463871576988584°
Real space, in pixels:
User's distance from window = 1511.8110673484
Mare Imbrium's radius = 12.2400203399425 pixels
minfeaturesize = 12.2277803421021 pixels
Set the minimum apparent radius in pixels that an orbit would need
in order to be rendered.
Smaller orbits will not be drawn.
A negative argument is treated as zero.
The default radius is 20 pixels,
restored by
Celestia:sane.
See also
Celestia:getminorbitsize.
Set the types of
Objects
whose orbits will be rendered if the
"orbits"
renderflag is
true.
The argument of
Celestia:setorbitflags
is a table of
boolean
values whose keys are the strings
"Asteroid",
"Comet",
"DwarfPlanet",
"Invisible",
"MinorMoon",
"Moon",
"Planet",
"Spacecraft",
"Star",
and
"Unknown".
A missing field has no effect on the existing orbitflags.
Celestia:sane
sets them to sane values.
See
Object:setorbitvisibility
for the complicated interactions between the renderflags and the orbitflags.
See also
Celestia:getorbitflags
and
Celestia:setlinecolor.
Specify the items to be displayed
in the transparent overlay atop the Celestia window.
The argument is a table of
boolean
values whose keys are the strings
"Frame",
"Selection",
"Time",
and
"Velocity".
A missing field has no effect on the overlay flags.
Celestia:sane
sets them to sane values.
See also
Celestia:getoverlayelements
and
Observer:setspeed.
Specify which things will be displayed.
The argument is a table of
boolean
values whose keys are the strings
"atmospheres",
"automag",
"boundaries",
"cloudmaps",
"cloudshadows",
"comettails",
"constellations",
"eclipseshadows",
"ecliptic",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"galaxies",
"globulars",
"grid",
"horizontalgrid",
"lightdelay",
"markers",
"nebulae",
"nightmaps",
"openclusters",
"orbits",
"partialtrajectories",
"planets",
"ringshadows",
and
"smoothlines".
A missing field has no effect on the existing renderflags.
Celestia:sane
sets them to sane values.
See
Object:setorbitvisibility
for the complicated interactions between the renderflags and the orbitflags.
See also
Celestia:getrenderflags,
Celestia:show,
and
Celestia:hide.
Set the star distance limit in lightyears.
Stars farther than this distance from the
Observer
will not be rendered.
The initial value of one million lightyears
(20 times the radius of the
Milky Way)
is restored by
Celestia:sane.
See also
Celestia:getstardistancelimit.
Set the star style to
"fuzzy",
"point",
or
"disc"
(case sensitive).
The initial value of
"fuzzy"
is restored by
Celestia:sane.
Use
"point"
for
astrometry
such as the parallax display in
parallax
or the CCD example in
screenShot.
The corresponding keystroke command is
control-s.
See also
Celestia:getstarstyle.
Set the red, green, and blue components of the color of the text printed by
Celestia:print
and
Celestia:flash.
See
celestiaPrint.
The arguments are clamped to the range 0 to 1 inclusive,
and the initial values of 1, 1, 1 are restored by
Celestia:sane.
The alpha level is 1.
Each number is stored internally as a whole number in the range
0 to 255 inclusive,
so the values returned by
Celestia:gettextcolor
may not be the same as the arguments of
Celestia:settextcolor.
Set the texture resolution to
0 for low,
1 for medium,
or 2 for high.
This determines whether the texture files are read from the
lores,
medres,
or
hires
subdirectories of the
textures
subdirectory of the Celx directory.
The initial value of 1 is restored by
Celestia:sane.
See also
Celestia:gettextureresolution.
Set the current TDB simulation time of the active
Observer;
see
settime.
An
Observer
can be made active by calling
Observer:makeactiveview.
If the
Observers
are synchronized
(with
Celestia:synchronizetime),
the simulation time of all the other
Observers
will be set to the same value.
Celestia can simulate times in the range
–730498278941.99951
to
730486721060.00073
inclusive,
corresponding to noon UTC on January 1st of the years
2,000,000,001 B.C. and 2,000,000,000 A.D.
(The function
wait
must be called after
Celestia:settime
in order to clamp the return value of
Celestia:gettime
to this range.)
The birth of the Moon and the death of the Sun are therefore out of range.
By default, the simulation time
is the same as the real time returned by
Celestia:getsystemtime,
but the former runs more smoothly.
See
Exponential.
The return value of
Celestia:utctotdb
can be passed to
Celestia:settime.
But the return value of
Celestia:tojulianday
must not be passed to
Celestia:settime;
see
tdb.
The corresponding keystroke commands are
command-t on Macintosh, and
! (exclamation point).
See also
Celestia:gettime
and
Celestia:settimescale.
Set the speed at which the simulation time passes for all
Observers.
See
settime.
The argument is in units of simulation time per unit of real time;
it can be positive, negative, or zero.
The initial value of 1 is restored by
Celestia:sane.
The corresponding keystroke commands are
j,
k,
l, and
\ (backslash).
See also
Celestia:gettimescale.
Set the number of real-time seconds that the Celx program can run
before it has to make the next call to the
wait
function.
The initial value of 5 is restored by
Celestia:sane
and by
wait.
Celestia:settimeslice
may be needed before a time-consuming loop through the stars in the database;
see the examples in
hertzsprungrussell
and
twoStars.
See also
Celestia:getscripttime.
Set the state of an
Observer
to the values in the URL given as the first argument.
The second argument defaults to the active
Observer.
The corresponding keystroke command is
command-v
on Macintosh and
control-insert
on Microsoft Windows.
See
Celestia:geturl
for the format of the URL,
and
std.tourl.
Draw or hide a one-pixel gray border around each view.
The default value of
true
is restored by
Celestia:sane.
The borders are visible only if there is more than one view.
See also
Celestia:windowbordersvisible
and
Observer:splitview.
Turn on the given renderflags
(renderFlags).
Do not call this method before
Celestia:sane,
since the latter sets the flags back to ther default values.
Celestia:show
accepts a variable number of the following case-sensitive strings:
"atmospheres",
"automag",
"boundaries",
"cloudmaps",
"cloudshadows",
"comettails",
"constellations",
"eclipseshadows",
"ecliptic",
"eclipticgrid",
"equatorialgrid",
"galacticgrid",
"galaxies",
"globulars",
"grid",
"horizontalgrid",
"lightdelay",
"markers",
"nebulae",
"nightmaps",
"openclusters",
"orbits",
"partialtrajectories",
"planets",
"ringshadows",
and
"smoothlines".
See also
Celestia:hide,
Celestia:getrenderflags,
and
Celestia:setrenderflags.
Show the names and stick-figure outlines of the specified constellations.
The argument is an array of case-insensitive constellation names from the
AsterimsFile
in
celestia.cfg.
With no argument,
all the constellations are shown.
In either case, the constellations are shown only if the
"constellations"
renderflag is
true.
Celestia:sane
shows all the constellations.
See also
Celestia:hideconstellations
and
Celestia:show.
Show the labels on the constellations and/or the celestial
Objects
of the given types.
Celestia:showlabel
accepts a variable number of the following case-sensitive strings:
"asteroids",
"constellations",
"comets",
"dwarfplanets",
"galaxies",
"globulars",
"i18nconstellations",
"locations",
"minormoons",
"moons",
"nebulae",
"openclusters",
"planets",
"spacecraft",
or
"stars".
If the labels for
"constellations"
are shown,
the constellation names will be shown.
If the labels for
"i18nconstellations"
are also shown,
the constellation names will be shown in Latin.
See also
Celestia:hidelabel,
Celestia:setlabelflags,
and
Celestia:showconstellations.
Return an iterator for looping through all the stars in the
StarDatabase
and
StarCatalogs
in
celestia.cfg.
See
loopDatabase
for an example.
A
“star”
may be a true star, neutron star, black hole,
or the barycenter of a stellar system.
See also
Celestia:getstar,
Celestia:getstarcount,
and
Object:spectraltype.
If the argument is
true,
give all
Observers
the simulation time of the active
Observer.
Any call to
Celestia:settime
will then set the simulation time of every
Observer.
Celestia:sane
calls
Celestia:synchronizetime
with the argument
true.
If the argument of
Celestia:synchronizetime
is
false,
allow the
Observers
to have different simulation times.
They all share the same timescale, however.
See also
Celestia:istimesynchronized.
Create an image file capturing the Celestia window.
See
screenShot.
The first argument is
"jpg"
or
"png",
defaulting to
"png".
The second argument specifies the middle part of the name of the image file.
This part can be at most 16 characters and defaults to the empty string
"".
It is restricted to letters, digits, and underscores;
other characters will be changed to underscores.
The arguments
"png"
and
"moon"
will create an image file named
screenshot-moon-000001.png.
The image files are consecutively numbered as long as Celestia keeps running.
If we quit Celestia and restart it,
the numbers start again at 1.
In this case,
be careful not to overwrite an existing image file.
The image file is placed in the
ScriptScreenshotDirectory
in
celestia.cfg.
If this directory is
"",
the image file is placed in the Celx directory.
A backslash in a filename must be doubled in Microsoft Windows.
The return value is
true
if the capture was successful.
On Macintosh,
Celestia:takescreenshot
does nothing and returns
false.
Convert a
TDB
time
(Barycentric Dynamical Time) to
UTC.
The return value is a table containing fields named
year,
month,
day,
hour,
minute,
seconds.
All but the last are whole numbers.
A year value of zero means 1 B.C.
See
tdb.
See also
Celestia:utctotdb,
Celestia:tojulianday,
and
Celestia:fromjulianday.
Convert a UTC date and time to a Julian date. The UTC date and time are expressed as six arguments giving the year, month, day, hour, minute, and seconds. They default to 0, 1, 1, 0, 0, 0; fractions in the first five arguments will be ignored. The month numbers range from 1 to 12 inclusive. A year number of 0 means 1 BC.
The return value of this method,
plus or minus a number of days (possibly with a fraction),
can be used only as the argument of
Celestia:fromjulianday.
Any other use will produce meaningless results.
In particular, the return value must not be used as the argument of
Celestia:settime
or
Celestia:tdbtoutc.
Celestia:tojulianday
follows two simple rules:
Celestia:tojulianday
is unaware that there was no year 0 A.D.
It’s also unaware
that the eleven days from September 3 to 13, 1752 did not exist.)
Celestia:tojulianday
believes that every day has 24 hours,
every hour has 60 minutes,
and every minute has 60 seconds.
See
leapSeconds
and
stepThrough
for using
Celestia:fromjulianday
and
tojulianday
for stepping through the calendar.
See also
Celestia:tdbtoutc,
Celestia:utctotdb,
and
Phase:timespan.
Remove the marker from the given celestial
Object.
The corresponding keystroke command is
control-p.
See also
Celestia:mark,
Celestia:unmarkall,
Object:mark,
and
Object:unmark.
Remove the markers from all celestial
Objects.
This method is called by
Celestia:sane.
See also
Celestia:mark,
Celestia:unmark,
Object:mark,
and
Object:unmark.
Convert a UTC time to TDB (Barycentric Dynamical Time). See tdb. The six arguments are the year, month, day, hour, minute, and second, defaulting to 0, 1, 1, 0, 0, 0. The fractional parts of the first five arguments are ignored. The month numbers range from 1 to 12 inclusive. A year value of zero means 1 B.C. The number of seconds can be greater than 60 if the minute contains a leap second.
See also
Celestia:tdbtoutc,
Celestia:tojulianday,
and
Celestia:fromjulianday.
Return
true
if the one-pixel gray border around each view is visible.
The borders are visible only if there is more than one view.
See also
Celestia:setwindowbordersvisible
and
Observer:splitview.
A
Celscript
object represents a script written in the language
Cel.
Class
Celscript
is implemented in
version/src/celestia/celx.cpp.
Usage:
--Create a Celscript object. --Distances are in kilometers. This distance is 1 microlightyear. local sourceCode = "{" .. " gotoloc {time 0 position [0 0 9460730.4725808]}\n" .. " print {text \"Hello\" duration 10 row -5}\n" .. "}" --Easier way to do create the same string: use Lua long brackets. local sourceCode = [[{ gotoloc {time 0 position [0 0 9460730.4725808]} print {text "Hello" duration 10 row -5} }]] local celscript = celestia:createcelscript(sourceCode) --Test if an object is a Celscript. if type(object) == "userdata" and tostring(object) == "[Celscript]" then
Execute a
Celscript
for one tick of the simulation,
approximately 1/60th of a second on my machine.
This method ignores its argument(s),
and returns
false
when the Cel script has finished.
It must be called continuously in a loop with a
wait
of zero seconds.
See also
Celestia:createcelscript
and
Celestia:runscript.
A
Font
represents a texture font (in a
.txf
file) used by
Celestia:print,
Celestia:flash,
Object:mark,
and the OpenGL functions.
The configuration file
celestia.cfg
specifies three of these fonts:
the
TitleFont,
LabelFont,
and plain old
Font.
See
inputFile
for a program that displays all the characters of a texture font.
Class
Font
is implemented in
version/src/celestia/celx.cpp.
Usage:
local font = celestia:getfont() local font = celestia:gettitlefont() local font = celestia:loadfont("fonts/default.txf") local font = celestia:loadfont("fonts/" .. celestia:getparamstring("LabelFont")) --Test if an object is a Font. if type(object) == "userdata" and tostring(object) == "[Font]" then
This method must be called before
Font:render;
see
opengl
for an example.
It passes the argument
GL_TEXTURE_2D
to the OpenGL function
glBindTexture.
Return the height in pixels of this font.
The return value is a whole number
giving the sum of the max ascent and max descent;
see
inputFile
for a program that gets these maxima.
Celestia:print
adds one pixel of leading between lines.
See
windowDimensions.
See also
Font:getwidth.
Return the width in pixels (a whole number)
of the argument string in this font.
See
windowDimensions.
See also
Celestia:gettextwidth.
Print the string in the Celestia window
at the location specified by
glu.Ortho2D
and
gl.Translate.
The amount of translation is specified in pixels.
The first argument of
glu.Ortho2D
plus the amount of horizontal translation must be a number that is
1/8
greater than an integer;
see
gl.TexelRound.
Similarly,
the third argument of
glu.Ortho2D
plus the amount of vertical translation must be a number that is
1/8
greater than an integer.
The method
Font:bind
must be called before
Font:render.
See
opengl
for a complete example.
A
Frame
of reference has perpendicular X, Y, Z axes
with distances measured in microlightyears.
See
framesOfReference.
The origin of the
Frame
may be at rest or attached to the center of a moving celestial
Object.
An axis of the frame may point in a constant direction,
or may depend on the orientation and/or position of one or two
celestial
Objects.
A
Position,
Vector,
and
Rotation
(i.e., an orientation)
are measured with respect to a
Frame.
Class
Frame
is implemented in
version/src/celestia/celx_frame.cpp.
The Celx Standard Library offers a
rotated frame,
implemented as a table containing a
Frame
and a
Rotation.
The following six
Frames
have the same origin as the above,
but their axes point in a different direction.
Here are three examples of rotated frames.
barycentricFrame
goes through the origin of the universal frame
and is parallel to the plane of the Earth’s equator.
It gives us a simple way to convert from universal coördinates
to barycentric right ascension and declination.
geocentricFrame
goes through the center of the Earth
and is parallel to the plane of the Earth’s equator.
It gives us a simple way to convert from universal coördinates
to geocentric right ascension and declination.
altazFrame
goes through the center of the Earth
and is parallel to the plane of the horizon at New York City.
It gives us a simple way to convert the
Vector
toBetelgeuse
from universal coördinates to altitude and azimuth.
Convert a
Position,
Vector,
or
Rotation
from the given
Frame
into the universal
Frame.
The opposite conversion is performed by
Frame:to.
Without the Celx Standard Library, the argument can only be a
Position
or
Rotation.
The argument
t
is the time at which the conversion is performed,
defaulting to the current simulation time.
It makes a difference if the
Frame
is in motion.
See also
Rotation:transform.
The following examples demonstrate what conversions of
Vectors
and
Rotations
do by defining them in terms of conversions of
Positions.
Return a string giving the type of the
Frame.
The possible return values are
"universal""ecliptic""equatorial""bodyfixed""chase""lock""invalid"
This method returns
"invalid"
for a
Frame
returned by
Object:bodyframe,
Object:orbitframe,
Phase:bodyframe
or
Phase:orbitframe.
The reason is that the C++ functions
object_bodyframe
and
object_orbitframe
in
version/src/celestia/celx_object.cpp,
and the functions
phase_bodyframe
and
phase_orbitframe
in
version/src/celestia/celx_phase.cpp,
pass a
ReferenceFrame
to the constructor for
ObserverFrame
in
version/src/celengine/observer.cpp.
This constructor initializes the
coordSys
data member of the
ObserverFrame
to
ObserverFrame::Unknown.
To get the
coördinate system,
look in the
.ssc
file for the
Object
or use the workaround below.
Return the reference
Object
of the
Frame.
For the universal
Frame,
the method returns
nil
because that
Frame
has no reference
Object.
Otherwise,
it returns the
Object
whose center is the origin of the
Frame.
See also
Observer:orbit.
Return the target
Object
of the
Frame.
For a lock
Frame,
it returns the
Object
towards whose center the X axis points.
Otherwise,
it returns
nil
because a non-lock
Frame
has no target
Object.
Convert a
Position,
Vector,
or
Rotation
from the universal
Frame
into the given
Frame.
The opposite conversion is performed by
Frame:from.
Without the Celx Standard Library,
the argument can only be a
Position
or
Rotation.
The argument
t
is the time at which the conversion is performed,
defaulting to the current simulation time.
It makes a difference for a
Frame
that is in motion.
See also
Rotation:transform.
The following examples demonstrate what conversions of
Vectors
and
Rotations
do by defining them in terms of conversions of
Positions.
An
Object
is a celestial object or a surface feature thereof.
It can also be a
barycenter
such as the
"Solar System Barycenter",
"Sol/Pluto-Charon",
or
"Sirius".
Constellations are not
Objects.
The behavior of several methods of class
Object
depends on whether the
Object
has a “body”,
which in turn depends on whether the
Object
belongs to our Solar System.
A quick way to check is by looking at the
Object’s
type.
One exception:
the only star that has a body is the Sun.
| has a body | has no body |
|---|---|
planet
|
star
|
These body-aware methods are
addreferencemark,
getinfo,
getphase,
setradius,
phases,
preloadtexture,
and
setvisible.
See also
Observer:lock.
To test if an
Object
has a body, call
Object:phases.
Objects
are not created or destroyed by a Celx program.
They are read from the
SolarSystemCatalogs,
StarDatabase,
StarCatalogs,
and
DeepSkyCatalogs
in the configuration file
celestia.cfg
when Celestia is launched.
There is also a special dummy
Object
that indicates
“no object is present”;
its
name
is
"?"
and its
type
is
"null".
The dummy is returned by
Celestia:oldfind,
Celestia:getselection,
and
Observer:gettrackedobject.
The Lua value
nil
is used instead of the dummy by
Frame:getrefobject,
Frame:gettargetobject,
and the
parent
field of the info table returned by
Object:getinfo.
Class
Object
is implemented in
version/src/celestia/celx_object.cpp.
Return the absolute magnitude of a star,
i.e., the apparent magnitude it would have from 10 parsecs away.
The value is derived from the
AppMag
(apparent magnitude)
in one of the
StarCatalogs
in
celestia.cfg
using the magnitude formula in
loopDatabase
and the values of
LY_PER_PARSEC
and
LN_MAG
(which is
5 / ln 100)
in
version/src/celengine/astro.h.
For example, the absolute magnitude of
Sirius A
is computed from the
AppMag
of
–1.43
in
version/data/nearstars.stc
(not the
–1.44
for HIP 32349 in
version/data/stars.txt).
If the star has no
AppMag
in the
StarCatalogs,
its absolute magnitude is read from
version/data/stars.dat
as a 16-bit integer divided by 256.
For example, the absolute magnitude of
Betelgeuse
is
–1400 / 256 = –5.46875.
A “star” that is a barycenter has an absolute magnitude of 30.
A non-star has an absolute magnitude of
nil.
See also the
bolomericMagnitude
and
luminosity
fields of the
info table.
Display an informative decoration on the
Object.
Call this method more than once
to give several reference marks of different types
to the same
Object
at the same time.
The reference marks can also be selected from the context menu
when you right-click on a celestial object.
The
Object
must have a body,
or Celestia will behave unpredictably.
(A star or galaxy has no body.)
The argument is a table containing a field named
type,
whose value is one of the following case-insensitive strings.
The arrows are implemented in
version/src/celengine/axisarrow.cpp.
The length of a velocity or spin vector does not show the
Object’s
speed,
unless we set it ourselves with the
size
field.
"body axes":
the axes of the
Object’s
bodyfixed frame.
The red X arrow is the bodyfixed X axis
at latitude
0°
North,
longitude
0°
Eeast.
The blue Z arrow is the bodyfixed Y axis
at latitude
90°
North.
The green Y arrow is the bodyfixed
–Z
axis at latitude
0°
North, longitude
90°
E.
"body to body direction":
an arrow pointing to another
Object.
It’s just like the
"sun direction"
below,
except that we get to pick the other
Object.
The color defaults to a subdued green
(0, .5, 0).
"frame axes":
the axes for the frame of reference in which the object’s
orientation is defined.
For the Earth,
the XZ plane of this frame is the plane of the ecliptic.
For other planets,
the XZ plane is the plane of the celestial equator.
The red X arrow is the X axis.
The blue Z arrow is the Y axis.
The green Y arrow is the
–Z
axis.
See
Object:bodyframe.
"planetographic grid":
lines of latitude and longitude in a light gray
(.8, .8, .8),
and the equator in a cyanic
(.5, 1, 1).
North and south are upside down for retrograde rotators such as
Venus.
Implemented in
version/src/celengine/planetgrid.cpp.
Note:
"planetographicgrid"
has no space in the arguments of
Celestia:setlabelcolor
and
Celestia:setlinecolor.
"spin vector":
an arrow pointing along the object’s rotational axis.
The arrow points north for most
Objects,
south for retrograde rotators such as
Venus.
The color defaults to a gray
(.6, .6, .6).
"sun direction":
an arrow pointing toward the Sun.
The color defaults to a sunny
(1, 1, 0).
"velocity vector":
an arrow pointing in the direction of the
Object’s
motion with respect to its primary.
If the
Object
is
Pluto
or
Charon,
the primary is the Pluto-Charon barycenter.
The color defaults to a nondescript
(.6, .6, .9).
"visible region":
a line along the surface of the
Object
showing the edge of the region where the target
Object
is visible.
If the target is the Sun, the line will be the terminator.
Since the Sun is the most common target,
the color defaults to
(1, 1, 0).
Implemented in
version/src/celengine/visibleregion.cpp.
The other fields of the table are
size:
in kilometers,
defaulting to the
Object’s
radius.
The size is ignored for types
"visible region"
and
"planetographic grid".
opacity:
ranges from 0 (transparent) to 1 (opaque).color:
a pound sign and six case-insensitive hexadecimal digits
(e.g. "#FFFF00"),
or one of the 140 case-sensitive colors listed in
version/src/celutil/color.cpp
(e.g. "yellow").
The color is ignored for types
"body axes",
"frame axes",
and
"planetographic grid".
tag:
a name for this reference mark so that it can be removed with
Object:removereferencemark.target:
specifies the other
Object
for types
"visible region"
and
"body to body direction".
See also
Object:removereferencemark
and
Object:mark.
Return the
Object’s
bodyfixed frame.
See
bodyfixedFrame.
Return the
Frame
with respect to which the
Object’s
orientation is defined at simulation time
t,
defaulting to the current simulation time.
For an
Object
with a
ScriptedRotation
(scriptedRotation),
the
Frame
is the equatorial frame of the
Object’s
primary.
For the Earth, the
Frame
is the Sun’s ecliptic frame.
For the other planets and natural satellites in the Solar System,
the
Frame
is the one whose origin is the
Object’s
primary and whose XZ plane is the plane of the celestial equator.
For
Objects
outside the Solar System,
the
Frame
is the universal
Frame.
See also
Phase:bodyframe.
The
getcoordinatesystem
method of the
Frame
returns the string
"invalid".
See that method for an explanation and workaround.
Return the catalog number of a star as a nonnegative 32-bit integer
in the range 0 to
232 − 1
inclusive.
The case-insensitive argument is
"HD"
for
Henry Draper,
"HIP"
for
Hipparcos,
or
"SAO"
for
Smithsonian
Astrophysical Observatory.
The return value is
nil
if the argument is not recognized or the
Object
doesn’t have the catalog number.
The Hipparcos numbers are read from the
StarDatabase
in
celestia.cfg,
and are listed in humanly-readable form in the first column of
version/data/stars.txt.
The Henry Draper and Smithsonian numbers are in the
HDCrossIndex
and
SAOCrossIndex
in
celestia.cfg.
See also the
catalogNumber
field of
Object:getinfo.
Return the
Object’s
equatorial frame.
See
equatorialFrame.
Return an iterator function for visiting all the descendants of an
Object.
These descendants form a tree
which the iterator traverses in preorder,
visiting each
Object
before the children of that
Object.
The root
Object
of the tree is at level zero.
See
Recursion.
See also
Object:getchildren.
Return an array of the
Object’s
immediate children (i.e., its satellites).
If there are none,
the array is empty but it is still an array.
To loop through
all
the descendants of an
Object
(the children, grandchildren, etc.),
see
Object:family.
Warning: some
Objects
do not acknowledge their paternity.
The parent of
"Sol"
is the
"Solar System Barycenter",
but the latter has no children.
Similarly, the parent of
"Sol/Earth/Washington D.C."
is
"Earth",
but the only children of
"Earth"
are satellites.
(See
Object:locations.)
Pluto,
on the other hand,
is the Œdipus Rex of the Solar System.
His parent is
"Sol",
but the children of
"Sol"
include
"Pluto-Charon"
as well as
"Pluto".
Return a table of unchanging information about the
Object.
See
infoTable.
The table always contains the following two fields.
The table also contains one of the following four sets of fields,
depending on the
type
of the
Object.
Numeric values are in float precision
(doubleArithmetic)
unless otherwise indicated.
Object
with a body.
Its
type
is one of
"planet",
"dwarfplanet",
"moon",
"minormoon",
"asteroid",
"comet",
"spacecraft",
"invisible",
"surfacefeature",
"component",
"diffuse".
albedo:
a dimensionless ratio in the range 0 (dull) to 1 (shiny).
See
temperatureDistance
for its use in temperature calculations.atmosphereCloudHeight:
in kilometers.
This field is present only if the
Object
has an
Atmosphere
in its
.ssc
file,
and defaults to zero if the
Atmosphere
has no
CloudHeight.
atmosphereCloudSpeed:
in radians per day.
A positive number rotates the clouds in the same direction
as the
Object.
This field is present only if the
Object
has an
Atmosphere
in its
.ssc
file,
and defaults to zero if the
Atmosphere
has no
CloudSpeed.
The
CloudSpeed
in the
.ssc
is in degrees per day.
atmosphereHeight:
in kilometers.
This field is present only if the
Object
has an
Atmosphere
in its
.ssc
file,
and defaults to zero if the
Atmosphere
has no
Height.
See the Mie scale height passed to
Object:setatmosphere.
hasRings:
a
boolean
value.
Read from the
Rings
field in a
.ssc
file,
defaults to
false.
In the standard distribution of Celestia,
Saturn,
Uranus,
and
Neptune
have rings;
Jupiter
does not.infoURL:
read from the
InfoURL
field in a
.ssc
file,
defaults to the empty string
"".lifespanEnd:
a TDB time in double precision.
The
Object
is visible only during its lifetime.
Defaults to
math.huge.
lifespanStart:
a TDB time in double precision.
Defaults to
-math.huge.mass:
in multiples of the Earth’s mass,
which is
5.976 · 1024
kilograms
in
version/src/celengine/astro.cpp.
Specified for extrasolar planets in the
.ssc
file; defaults to zero.
oblateness:
a
dimensionless
ratio in the range 0
(perfectly spherical) to 1 (a disk).
Defaults to zero if not specified in the
.ssc
file.
Multiply the
radius
field by
1 − oblateness
to get the polar radius.
orbitPeriod,
in days.
Read from the
Period
field of an
EllipticalOrbit,
or from a
CustomOrbit,
in a
.ssc
file.parent:
the
Object’s
primary.
Every
Object
in the Solar System has a parent
Object,
except the
"Solar System Barycenter"
whose parent is
nil.
The parent of
"Sol"
is the
"Solar System Barycenter".
The parent of
"Sol/Cassini/Huygens"
is
"Sol/Cassini",
even though
Huygens
does not revolve around
Cassini.
See the other anomalies in
Object:getchildren.radius:
equatorial radius in kilometers.
Read from the
Radius
field in a
.ssc
file; defaults to 1.
Multiply by
1 − oblateness
to get the polar radius.
For a comet, this field is the radius of the nucleus.
For a barycenter, this field is 1.
rotationPeriod,
in days.
Read from the
Period
field of a
RotationPeriod,
or from a
CustomRotation,
in a
.ssc
file.
Defaults to zero.Object
of
type
"star".
Some of the fields are read from the
StarDatabase
and
StarCatalogs
files;
others are derived from other fields.
absoluteMagnitude:
same as the return value of
Object:absmag.
bolometricMagnitude:
derived from the absolute magnitude by adding the
bmag_correction
for the stellar class in
version/src/celengine/star.cpp.
catalogNumber,
a nonnegative 32-bit integer.
This is the Hipparcos number,
or the numbers above
1,000,000,000
in
version/data/extrasolar.stc.
Otherwise the stars are given numbers descending from
232 − 2 = 4,294,967,294
in the order in which they are listed in the
StarCatalogs
in
celestia.cfg.
See also
Object:catalognumber.
luminosity,
in multiples of the Sun’s luminosity,
which is
3.8462 · 1026
watts in
version/src/celengine/astro.cpp.
The luminosity
L
is derived from the absolute magnitude
M
with the formula
L =
(100.2)(4.83
– M),
where
100.2
is the factor by which the luminosity increases
when the magnitude decreases by 1,
and 4.83 is the absolute magnitude of the Sun
in
version/src/celengine/astro.h.
orbitPeriod,
in days.
Read from the
Period
of an
EllipticalOrbit
in a
.stc
file.
If the star does not orbit a barycenter,
its orbit period is
nil.
The Sun’s orbit period is zero.
parent:
the barycenter
Object
around which the star revolves,
or
nil
if there is no parent.
The
stellarClass
of a stellar barycenter is
"Bary".
radius:
in kilometers.
Read from the
Radius
in a
.stc
file.
Otherwise the radius is derived from the star’s luminosity and temperature
with the formula in
temperatureDistance.
For a stellar barycenter, this field is .001 kilometers.
rotationPeriod,
in days.
Read from the
RotationPeriod
in a
.stc
file.
Otherwise read from the
rotperiod
arrays in
version/src/celengine/star.cpp.
The rotation period of a barycenter is 1.
stellarClass:
same as the return value of
Object:spectraltype,
quod vide.
temperature in Kelvin,
read from the stellar class tables in
version/src/celengine/star.cpp.
"galaxy",
"globular",
"opencluster",
or
"nebula".
The standard distribution has no open clusters or nebulæ.
absoluteMagnitude:
read from the
AbsMag
in a
.dsc
file;
defaults to
–1000.
catalogNumber:
descending from
232 − 2 = 4,294,967,294
in the order in which they are listed in the
DeepSkyCatalogs
in
celestia.cfg.
hubbleType:
read from the
Type
in a
.dsc
file;
defaults to
"Irr"
(irregular).
This field is present only if the
Object
is of type
"galaxy".
radius:
in lightyears (not microlightyears).
Read from the
Radius
in a
.dsc
file;
defaults to 1.
The
Object:radius
method is in kilometers."location".
A location on the surface of another
Object,
including craters, landing sites, cities, etc.
featureType:
read from the
Type
in a
.ssc
file.
One of
"astrum",
"catena",
"chaos",
"chasma",
"city",
"corona",
"crater",
"dorsum",
"farrum",
"fluctus",
"fossa",
"insula",
"landingsite",
"linea",
"mare",
"mensa",
"mons",
"observatory",
"other",
"patera",
"planitia",
"planum",
"regio",
"reticulum",
"rima",
"rupes",
"terra",
"tessera",
"tholus",
"undae",
"vallis",
"volcano".
The default is
"other".
See
Observer:getlocationflags
and
Observer:setlocationflags.
importance:
read from the
Importance
in a
.ssc
file;
defaults to
–1.
Used by
Celestia:setminfeaturesize.
infoURL:
defaults to the empty string
"".
parent:
the
Object
on which the location is located.
size:
diameter in kilometers,
defaults to 1.
Twice the value of the
Object:radius
method.
Return the
Phase
that this
Object
is in at TDB simulation time
t,
defaulting to the current simulation time.
Return
nil
if the
Object
has no body.
See also
Object:phases.
Return the
Position
of the center of this
Object
at TDB simulation time t,
defaulting to the current simulation time.
The
Position
is measured with respect to the universal
Frame.
Return the
Object’s
name in the natural language to which Celestia has been set.
On each platform,
the language for
Object:localname
is set in a different way.
Celestia.app/Contents/Resources
sibling directory of the Celx directory
(celxDirectory)
to see what languages are available.
(Additional languages can be created with the
POConverter
that you get when compiling Celestia from its source code;
see
compileMacintosh.)
Then go to the apple menu and select
locale
subdirectory of the Celx directory
(celxDirectory)
to see what languages are available.
Then set the
LC_ALL
environment variable in the
Command Prompt window.
LC_ALL
has an underscore, not a dash.
help set
set LC_ALL
set LC_ALL=fr
set LC_ALL
myprog.celx
/usr/local/share/locale/
sibling directory of the Celx directory
(celxDirectory)
to see what languages are available.
Then set the
LC_ALL
environment variable to a language and a country,
e.g.
pt_BR
for “Portuguese Brazil”.
If the
locale
directory contains your language but not your country,
go ahead and use your country anyway.
For example,
if
locale
contains
fr.lproj,
you can set
LC_ALL
to
fr_CA
for “French Canada”.
man locale
echo $LC_ALL
export LC_ALL=fr_CA
echo $LC_ALL
To pass the environment variable only to Celestia,
and not to any other program,
type the following Linux command.
The
/pathname/of/
is necessary only if the executable
Celestia
is in a directory that is not in your
PATH.
The
-f
argument is necessary only if
Celestia has been compiled
--with-glut
(compileLinux).
LC_ALL=fr_CA /pathname/of/celestia -f myprog.celx
See also
Object:name
and
Object:pathname.
The Lua function
os.setlocale
sets the locale for
os.date;
see
realTime
and
std.dayName.
Return an iterator for looping through all the location
Objects
on the surface of this
Object.
Mark the
Object
with a symbol and label.
An
Object
can have only one mark at a time;
a second call to
mark
will be ignored unless the
Object
is first
unmarked.
Object:mark
is more flexible than
Celestia:mark.
It has six arguments;
trailing ones may be omitted.
"#FFFF00"),
or one of the 140 case-sensitive colors listed in
version/src/celutil/color.cpp
(e.g. "yellow").
The default is
"#00FF00" =
"lime".
"circle",
"diamond",
"disk",
"downarrow",
"filledsquare",
"leftarrow",
"plus",
"rightarrow",
"square",
"triangle",
"uparrow",
"x".
The default is
"diamond".
Drawn by the member function
MarkerRepresentation::render
in
version/src/celengine/marker.cpp.
LabelFont
in
celestia.cfg.
Defaults to the empty string
"";
can’t include the newline character
\n.
true
if the mark can be blocked by an
Object.
Defaults to
true.
The corresponding keystroke command is
control-p.
See also
Object:unmark,
Celestia:unmarkall,
and
Object:setradius.
Return the name of the
Object.
The name does not include the pathname
(e.g., it’s "Earth",
not
"Sol/Earth").
A solar system
Object
gets its name from its
.ssc
file.
A star gets its name from the
StarNameDatabase
in
celestia.cfg,
indexed by Hipparcos numbers.
A deep sky object (globular cluster or galaxy)
gets its name from the
DeepSkyCatalogs
in
celestia.cfg.
In each case,
Object:name
returns only the first name of the
Object
in the database.
For a star,
it prefers a name in Arabic, Latin, Greek, or even English
(try
"The Garnet Star").
Otherwise it returns the star’s
Bayer
or
Flamsteed
designation.
As a last resort,
it returns one of the catalog numbers.
To get all the names of a star, see
inputFile.
See also
Object:localname
and
Object:pathname.
Return
true
if permission is currently granted by
Object:setorbitcoloroverridden
to allow
Object:setorbitcolor
to set the color of the
Object’s
orbit.
Return the
Frame
with respect to which the
Object’s
position is defined at simulation time
t,
defaulting to the current simulation time.
Given the standard
data/solarsys.ssc
file,
the Sun’s orbit
Frame
is the universal
Frame.
For other Solar System
Objects,
including ones with
ScripedOrbits,
the orbit
Frame
is the ecliptic
Frame
of the
Object’s
primary.
For an
Object
outside the Solar System,
the orbit
Frame
is the universal
Frame.
See also
Phase:orbitframe.
The
getcoordinatesystem
method of the
Frame
returns the string
"invalid".
See that method for an explanation and workaround.
Return the visibility of the
Object’s
orbit.
Warning: the argument of
Object:setorbitvisibility
is one of
"always",
"sometimes",
or
"never".
See
Object:setorbitvisibility
for the complicated interaction between the renderflags and the orbit flags.
Return the full pathname of an
Object.
For the algorithm, see the
repeat-until
loop in
keyExists.
See also
Object:name
and
Object:localname.
Return an iterator for looping through the
Phases
of an
Object
that has a body.
See also
Object:getphase.
Load the texture files for this
Object
now,
so we won’t have to wait for them to be loaded later.
Nothing happens if the
Object
has no body.
Return the
Object’s
equatorial radius in kilometers.
The radius of a star is
read from the
Radius
field in one of the
StarCatalogs
in
celestia.cfg.
If the star has no
Radius,
its radius is derived from the star’s luminosity and temperature
with the formula in
temperatureDistance.
The radius of a stellar barycenter is .001 kilometers.
For non-stars,
the radius is read from the
Radius
in one of the
SolarSystemCatalogs
in
celestia.cfg.
It defaults to 1 kilometer for a Solar System
Object
and to
9,460,730,822,656 kilometers
(1 lightyear in single precision,
doubleArithmetic)
for a deep sky object
(galaxy, globular cluster, open cluster, or nebula).
The radius of a comet is the radius of its nucleus,
in kilometers.
Warning: the
radius
field of a deep sky object’s
info table is in lightyears, not microlightyears.
For other types of
Object,
the field is in kilometers.
Remove a reference mark.
The mark is identified by its tag string set by
Object:addreferencemark.
Modify the
Object’s
existing atmosphere.
If the
Object
has a body and already has an atmosphere
(from an
Atmosphere
field in its
.ssc
file),
the method will be successful and will write
"set atmosphere\n"
to Celestia’s standard output.
Rayleigh scattering is caused by particles much smaller than the wavelength of the light (e.g., molecules). It is very dependent on the wavelength. Mie scattering is caused by larger particles (e.g., water droplets). It is much less dependent on the wavelength.
The first 18 arguments form six trios of red, green, blue.
This method does not set the atmosphere height;
you’ll have to set the
Height
parameter of the
Atmosphere
in the
.ssc
file.
See
Object:setradius.
Object’s
surface.Object’s
surface.
Blue should scatter more than red,
since the amount of scattering is inversely proportional to
the fourth power of the wavelength,
and blue has a smaller wavelength.
Object’s
surface.
Object’s
surface.
AtmosphereExtinctionThreshold
in
version/src/celengine/renderglsl.cpp.
See the
atmosphereHeight
field of
Object:getinfo
and the exercise in
celestialDome.
Set the red, greem, and blue components of the color of the
Object’s
orbit when the
Object
is not selected.
Each argument is clamped to the range 0 to 1 inclusive
and then stored as an 8-bit integer in the range 0 to 255 inclusive.
The alpha level is 1.
For the default color of the orbit of each type of
Object,
see the
OrbitColors
in
version/src/celengine/render.cpp.
This method does nothing unless permission has been granted by
Object:setorbitcoloroverridden.
See also
Object:orbitcoloroverridden.
Grant (or deny) the method
Object:setorbitcolor
permission to set the color of the
Object’s
orbit.
See also
Object:orbitcoloroverridden.
Set the visibility of the
Object’s
orbit.
The argument (case-sensitive) is
"always",
"sometimes",
or
"never".
(Warning: the return value of
Object:orbitvisibility
is one of
"always",
"normal",
or
"never".)
The default visibility is
"sometimes"
=
"normal".
The orbit visibility interacts with the renderflags and the orbitflags as shown in the following fragment. But first, three warnings.
Celestia:sane
hides
the
"orbits".Objects
cannot be compared with the
==
operator;
compare their
pathnames
instead.Object:type
returns a lowercase string such as
"planet"
or
"moon",
while the orbitflags keys are capitalized strings such as
"Planet"
or
"Moon".
We therefore apply
string.upper
to the first letter of the type.
string.gsub("^%l", string.upperstring.upper)]
then
--object's orbit is visible
else
--object's orbit is not visible
end
Set the
Object’s
radius in kilometers to the given value.
Useful for magnifying the planets in an overview of the Solar System.
If the
Object
has no body,
this method will be ignored.
If the
Object
is non-spherical,
its longest semiaxis will be set to the given value
and the other dimensions will be scaled accordingly.
Object:setradius
will scale the
Object’s
rings but not its atmosphere;
see below.
A positive argument will scale the
Object
and its rings;
a zero argument will scale only the rings.
(Want to see what
Saturn
would look like without its rings?)
Warning: if the argument is zero,
the radius will stay zero until Celestia is relaunched.
And a negative argument will confuse Celestia.
If the
Object’s
radius is increased,
its surface locations will no longer be labelled
and their marks will have to be set to non-occludable.
See the first example below and
Object:mark.
--[[
Display the inner Solar System with the planets magnified. The plane of the
Solar System lies in the plane of the window, with the Solar System barycenter
at the center. The vernal equinox in Pisces is off the right edge of the
window; the supper solstice in Taurus/Gemini is off the top edge.
]]
require("std")
local function main()
local observer = celestia:sane()
celestia:hide("grid")
celestia:setorbitflags({Planet = true, Moon = false})
celestia:show("orbits")
celestia:hidelabel("dwarfplanets", "comets", "constellations",
"galaxies", "minorplanets", "planets", "stars")
local astronomicalUnits = 5 --observer's height above plane of S System
local microlightyears = 1000000 * astronomicalUnits / std.auPerLy
local position = celestia:newposition(0, microlightyears, 0)
observer:setposition(position)
observer:lookat(std.position0, -std.zaxis)
--[[
Magnify the planets. The magnified Earth will engulf the Moon.
Since a star has no body, it cannot be magnified by a Celx script.
]]
local sol = celestia:find("Sol")
for level, object in sol:family() do
if object:type() == "planet" or object:name() == "Pluto" then
object:setradius(2400 * object:radius())
end
end
--one Earth day of simulation time per 2 seconds of real time
local day = celestia:find("Sol/Earth"):getinfo().rotationPeriod
celestia:settimescale(60 * 60 * 24 * day / 2)
wait()
end
main()
On some platforms,
setradius
may cause funny, moving spots to appear in the
Object’s
atmosphere.
A quick workaround is to hide the atmosphere.
The problem can be corrected by
scaling the atmosphere to agree with the
Object’s
new radius.
For example, when scaling the Earth by the above factor of 2400,
make the following five changes to its
Atmosphere
in
data/solarsys.ssc.
Note that
Object:setatmosphere
cannot change the atmosphere height.
Make the
Object
visible (or invisible),
together with its atmosphere, clouds, rings,
orbit, label,
and
referencemarks.
This method does not affect the
Object’s
satellites,
globular clusters,
or
mark.
The argument is a
boolean.
This method is ignored unless the
Object
has a body or is a deep sky object.
Stars are always visible;
the other
Objects
are visible by default.
This method is useful if the
Observer
is positioned inside of an
Object
and you want a clear view of the Universe outside of it.
See also
Object:visible.
If the
Object
is of
type
"star",
return the
Object’s
spectral type.
Otherwise, return
nil.
The spectral type is read from the
StarDatabase
in
celestia.cfg,
or from a
SpectralType
in one of the
StarCatalogs.
Every star has a spectral type: there is no default.
The spectral type is a string of at most 7 characters,
formatted in class
StarDetails
in
version/src/celengine/star.cpp.
It would be a lot easier to parse if a Lua
Pattern
could contain the
|
operator to separate alternatives.
Return the type of the
Object
as one of the following strings.
The first 11 types are the ones that have bodies.
"planet",
e.g.
"Sol/Earth"
or the extrasolar planet
"Pollux/b".
"dwarfplanet",
e.g.
the ex-asteroid
"Sol/Ceres",
the ex-planet
"Sol/Pluto",
or the
trans-Neptunian
"Sol/Eris"."moon":
a moon discovered by Earth-based observation,
e.g.
"Sol/Earth/Moon",
"Sol/Mars/Phobos",
or
"Sol/Eris/Dysnomia".
"minormoon":
mostly moons discovered by spacecraft,
but includes
"Sol/Pluto/Nix"
even though it’s bigger than
Phobos.
"asteroid",
e.g.,
"Sol/Pallas",
"Sol/Ida",
"Sol/Ida/Dactyl".
"comet",
e.g.
"Sol/Halley".
"spacecraft",
e.g.,
"Sol/Earth/Hubble",
"Sol/Cassini",
or
"Sol/Cassini/Huygens".
Warning: a spacecraft is visible only between its
lifespanStart
and
lifespanEnd."invisible",
e.g. the
Pluto-Charon barycenter
"Sol/Pluto-Charon"."surfacefeature".
No examples in the standard distribution."component".
No examples in the standard distribution."diffuse".
No examples in the standard distribution."unknown"
No examples in the standard distribution."star":
includes plain old stars such as
"Sirius A",
stellar system barycenters such as
"Solar System Barycenter"
and
"Sirius",
neutron stars such as
"PSR 1257+12",
and black holes.
(No black holes in the standard distribution.)
Get the spectral class from
Object:spectraltype
or from the
stellarClass
field of the star’s
info table."opencluster",
e.g., the
Pleiades
or
Hyades.
Less concentrated than a globular cluster;
no examples in the standard distribution."nebula":
a cloud of gas such as the
Orion Nebula.
No examples in the standard distribution."globular",
a globular cluster of stars such as
"M 13"
(one space after the
M)
in
Hercules.
In the standard distribution,
the
Milky Way
is the only galaxy with
globular clusters."galaxy",
e.g. the
Andromeda Galaxy
"M 31"
(one space after the
M).
Get the Hubble classification from the
hubbleType
field of the galaxy’s
info table."location",
e.g.
"Sol/Earth/Washington D.C."."null":
the type of the
Object
returned by
Celestia:getselection
and
Celestia:oldfind
when they didn’t find what they were looking for.
Return
true
if the
Object
is currently set to visible with
Object:setvisible,
or if its visibility was never tampered with.
Remove a mark that was displayed with
Object:mark
or
Celestia:mark.
The corresponding keystroke command is
control-p.
See also
Celestia:unmark
and
Celestia:unmarkall.
An
Observer
is a point of view in the simulated universe.
It (conventionally, “he”) has a
Position
and an orientation.
The orientation is expressed as a
Rotation
and determines the
Observer’s
direction of view and the
direction he thinks is “up”.
An
Observer
has two
Frames
of reference.
Position
of the
Observer.
The X axis always points to his right,
the Y axis to his zenith,
and the Z axis to his rear.
The only methods that use this frame are
Observer:rotateObserver:rotate
(rotateObserver)
and
Observer:orbitObserver:orbit
(orbitObserver).
The frame is also used in the “left-to-right”
interpretation of quaternion multiplication
(quaternionMultiplication).
setframed.
The
Observer
adheres to this
Frame,
i.e.,
he maintains a constant
Position
and orientation with respect to the
Frame
unless disturbed by a keystroke command or a Celx method call.
By default this
Frame
is the universal
Frame,
but he can be
setframed
to a different
Frame.
As the origin and/or orientation of this
Frame
changes,
the
Observer
will move and/or rotate with it.
The methods that change an
Observer’s orientation
with respect to this
Frame
are
center,
centerorbit,
goto,
gotodistance,
gotolocation,
gotolonglat,
gotosurface,
lookat,
rotate,
setorientation,
setspeed,
and
track.
The attributes of an
Observer
also include his
field of view,
his table of
location flags,
his
speed,
his
surface
(set of image files),
his
current simulation time,
and his
tracked object.
The Celestia window initially consists of one big view.
The method
Observer:splitview
divides a view into two subviews,
each with its own
Observer.
The methods of class
Observer
that deal with multiple views are
splitview,
deleteview,
singleview,
makeactiveview,
and
isvalid.
See also
Celestia:synchronizetime
and
Celestia:istimesynchronized.
No
Observers
exist during the execution of the files that create Lua hooks
(luaHookFunctions),
scripted orbits
(scriptedOrbit),
or scripted rotations
(scriptedRotation).
At any other point in real time,
one
Observer
is the active
Observer
and its view is the
active view.
The active
Observer
is distinguished by the following.
Celestia:getobserver.Observer
created by
Observer:splitview.
Celestia:settime.
(The other
Observers
may be set as well; see
Celestia:istimesynchronized.)
Class
Observer
is implemented in
version/src/celestia/celx_observer.cpp
and
version/src/celengine/observer.cpp.
If the
Observer
is executing a
goto,
center,
centerorbit,
etc.,
stop it.
Observer:cancelgoto
is called by
Celestia:sane.
See also
Observer:goto
and
Observer:travelling.
Orient the
Observer
so that the
Object
is centered in his field of view.
His forward vector will be aimed at the center of the
Object,
so he must be somewhere else on pain of division by zero.
This method does not change his position.
The second argument is the number of real-time seconds
that the
center
will take.
It defaults to 5,
which is the value of
std.duration.
To prevent other Celx statements
from executing while the
center
is in progress,
wait
for the same number of seconds.
See also
Observer:goto,
Observer:lookat,
and
Observer:track.
Orbit the
Observer
around the reference
Object
of the
Frame
to which he has been
setframed.
While the orbit is in progress,
the reference
Object
remains at the same location in the Celestia window.
In other words,
the
Observer’s
orientation
with respect to the reference
Object
remains unchanged.
The first argument of this method is an
Object.
The orbit continues until the argument
Object
is approximately centered in the window.
The centering is only approximate because the orbit actually continues until
the
Observer’s
forward
Vector
becomes parallel to the
Vector
from his
original
Position
towards the reference
Object.
The error will be small if the radius of the reference
Object
is small compared to the distance to the argument
Object.
The orbit is determined by the following
Vectors.
Vector
from the
Observer’s
initial position
towards the
Object
to be centered
Observer’s
forward
Vector
in his initial
orientation
The axis of the orbit is the cross product of the above
Vectors;
the angle of the orbit is the angle between the
Vectors.
See
Earthrise
for a tutorial example.
The second argument is the number of real-time seconds
that the
centerorbit
will take.
It defaults to 5,
which is the value of
std.duration.
To prevent other Celx statements
from executing while the
centerorbit
is in progress,
wait
for the same number of seconds.
See also
std.duration.
Adhere the
Observer
to the chase
Frame
(chaseFrame)
of the
Object.
The corresponding keystroke command is
"
(double quote).
Delete the
Observer
and his view.
Every method of a deleted
Observer
prints the message
“Bad observer object
(maybe tried to access a deleted view?)!”
A variable that refers to such an
Observer
should therefore be
local
so that it can be destroyed immediately after the
deleteview.
Nothing happens if you try to delete the last
Observer.
The corresponding keystroke command is
delete.
See also
Observer:splitview
and
Observer:isvalid.
Adhere the
Observer
to the ecliptic
Frame
(eclipticFrame)
of the
Object.
For an example,
watch the retrograde motion of Mars in
retrogradeMars.
The corresponding keystroke command is uppercase F.
Return the
Observer’s
vertical field of view in radians.
See
fieldOfView.
It’s displayed in degrees in the lower right corner of the
Celestia window.
The argument of
Observer:setfov
is clamped to the range
.001°
to
120°
inclusive, in radians.
But if the field of view is not already at its minimum or maximum,
the keystroke commands . and , (period and comma) can multiply and divide
it by
1.05.
See also
Celestia:getscreendimension
and the following methods of class
Observer:
setfov,
gethorizontalfov,
sethorizontalfov,
getverticalfov,
setverticalfov,
getmagnification,
and
setmagnification.
See also
std.gethorizontalfov
and
std.getverticalfov.
Return the
Frame
of reference to which the
Observer
has most recently been
setframed,
or the universal
Frame
if no such call has been made.
Return the horizontal field of view in radians
that would be subtended by a rectangle centered in the window,
given the
Observer’s
current level of
magnification.
The arguments are the width and height of the rectangle in pixels,
defaulting to the window dimensions returned by
Celestia:getscreendimension.
The return value of
Observer:gethorizontalfov
is therefore the
Observer’s
horizontal field of view only if the window is not
splitviewed.
std.gethorizontalfov
does not take the
Observer’s
current
magnification
into account.
See also
Observer:getfov,
Observer:getverticalfov,
and
Observer:sethorizontalfov.
Return a table of
boolean
values showing the types of features that will be labelled
for this
Observer.
The keys are mostly in Latin:
astrum (star),
catena (chain),
chaos,
chasma (hole),
city,
corona (oval),
crater,
dorsum (ridge),
farrum (pancake),
fluctus (outflow),
fossa (depression),
insula (island),
landingsite,
linea (line),
mare (sea),
mensa (mesa),
mons (mountain),
observatory,
other (miscellaneous),
patera (bowl),
planitia (low plain),
planum (high plain),
regio (region),
reticulum (netlike pattern),
rima (fissure),
rupes (scarp),
terra (land),
tessera (complex ridges),
tholus (dome),
undae (dunes),
vallis (valley),
volcano.
These names appear as the value of the
featureType
field of the info table
of a location;
see
Object:getinfo.
The
Font
of a label is the
LabelFont
in
celestia.cfg,
which defaults to the
Font
in
celestia.cfg,
which defaults to
default.txf.
Warning:
Celestia:sane
turns all the location flags on,
but it turns the
locations
field of the label flags off.
See also
Observer:setlocationflags.
Return the
Observer’s
magnification.
See
Magnification.
The default magnification is 1.
If the magnification is doubled,
the diameter of the field of view is halved.
The magnification is displayed in the lower right corner of the Celestia window.
See also
Observer:setmagnification
and
Observer:getfov.
Return the
Observer’s
orientation at the current simulation time.
See
getOrientation.
The return value is the
Rotation
which, when applied to the initial orientation, would produce
his current orientation.
The initial orientation faces towards
z = –∞,
with
y = ∞
overhead.
In other words,
it faces towards the
summer solstice
in
Taurus/Gemini,
with the north pole of the ecliptic in
Draco
overhead.
The axis of the orientation (i.e., its imaginary part)
is always measured with respect to the universal frame,
even if the
Observer
has been
setframed
to another
Frame.
See also
Observer:setorientation.
Return the
Observer’s
Position
at the current simulation time.
See
observerSetposition.
This method does not have
the optional time argument that
Object:getposition
has.
The position is always measured with respect to the universal frame,
even if the
Observer
has been
setframed
to another
Frame.
See also
Observer:setposition.
Return the
x,
y
coördinates of the pixel where the given
Position
will be displayed in the Celestia window.
See
project.
The purpose of this method is to let us draw OpenGL graphics
that point to positions of interest in the simulated universe.
It returns the correct values only if the window is not
splitviewed.
The
Position
is in the universal
Frame.
If the
Position
is outside of the window,
e.g, if it is behind the
Observer,
the method returns
nil,
nil.
Otherwise it returns
x,
y
coördinates (not necessarily whole numbers) measured from an origin
(0, 0)
at the center of the Celestia window,
with
x
increasing to the right and
y
increasing upwards.
See also
Celestia:getscreendimension.
Return the
Observer’s
speed in microlightyears per second of real time.
The speed is measured with respect to the
Frame
to which the
Observer
has been
setframed.
See also
Observer:setspeed.
--[[
Display the observer's speed in kilometers per real-time second with respect to
the frame to which he has been setframed. We have to call
Celestia:getscripttime because Celestia:getsystemtime is updated only once per
second.
]]
require("std")
local observer = celestia:sane()
local earth = celestia:find("Sol/Earth")
local frame = celestia:newframe("ecliptic", earth)
local oldPosition = nil
local oldTime = nil
local function tickHandler()
local position = frame:to(observer:getposition())
local time = celestia:getscripttime()
if oldPosition ~= nil and oldTime ~= nil then
local kilometers = position:distanceto(oldPosition)
local seconds = time - oldTime --seconds of real time
if seconds > 0 then
local s = string.format(
"%.1f\n"
.. "kilometers per second",
kilometers / seconds)
celestia:print(s)
end
end
oldPosition = position
oldTime = time
end
local function main()
observer:setframe(frame)
observer:setposition(std.position)
observer:setspeed(1 / KM_PER_MICROLY) --1 kilometer per real-time second
celestia:registereventhandler("tick", tickHandler)
end
main()
With an occasional jitter to 0.9, the output settles down to the following.
1.0 kilometers per second
Return the string to which this
Observer
has been
setsurfaced.
It represents the set of texture files that will be painted
on the surface of a celestial
Object.
The return value is the empty string
""
if the
Observer
has not yet been
setsurfaced.
Return the
Observer’s
current simulation time.
If the
Observers
are synchronized,
it will be the same time for all of them.
See
Celestia:synchronizetime,
Celestia:istimesynchronized,
Celestia:settime,
and
Observer:makeactiveview.
Return the
Object
that the
Observer
is tracking.
If tracking is turned off,
return the dummy
Object
whose
name
is
"?"
and whose
type
is
"null".
See
clouds.
See also
Observer:track.
Return the vertical field of view in radians
that would be subtended by a rectangle centered in the window,
given the
Observer’s
current level of
magnification.
The arguments are the width and height of the rectangle in pixels,
defaulting to the window dimensions returned by
Celestia:getscreendimension.
The return value of
Observer:getverticalfov
is therefore the
Observer’s
vertical field of view only if the window is not
splitviewed.
std.getverticalfov
does not take the
Observer’s
current
magnification
into account.
See also
Observer:getfov,
Observer:gethorizontalfov,
and
Observer:setverticalfov.
Move the
Observer
in a straight line to a given
Position,
or towards (or away from) the center of a given
Object.
The first argument can be a
Position
in universal coördinates,
an
Object,
or a
table
of parameters.
The table gives the fullest control.
The other two arguments are defined in terms of the table fields.
See also
Observer:setposition
and
Observer:orbit.
Even if the duration of the
goto
is zero seconds of real time,
it must still be followed by a
wait
to prevent the following statements from executing at the same time as the
goto.
See animateRotation for an example where the first argument is a table. In this case there must be no other arguments. The eight fields of the table are case sensitive, some of them with embedded uppercase letters.
duration:
the number of seconds of real time
the
goto
should take.
It defaults to 5,
which is the value of
std.duration.
To ensure that nothing else happens while the
goto
is in progress,
it can be followed
with a
wait
of the same duration.
accelTime:
the fraction of the first half of the duration
that will be spent in acceleration.
The same fraction of the second half will be spent in deceleration.
The value is clamped to the range .1 to 1 inclusive,
and defaults to .5.
This default value would make the
Observer
accelerate for the first quarter of the duration,
decelerate for the last quarter,
and cruise at a constant speed for the middle half of the duration.
from:
the starting
Position,
in universal coördinates.
The default is the
Observer’s
current
Position.
to:
the ending
Position,
in universal coördinates.
The default is the
Observer’s
current
Position.
initialOrientation:
the starting orientation,
expressed as a
Rotation
whose axis is in universal coördinates.
The default is the
Observer’s
current orientation.
finalOrientation:
the ending orientation,
expressed as a
Rotation
whose axis is in universal coördinates.
The default is the
Observer’s
current orientation.
startInterpolation:
the fraction of the duration that should elapse
before the change of orientation starts.
The value is clamped to the range 0 to 1 inclusive,
and defaults to .25.endInterpolation:
the fraction of the duration that should elapse
after the change of orientation ends.
The value is clamped to the range 0 to 1 inclusive,
and defaults to .75.
If the first argument of the
goto
is a
Position,
the
Observer
goes there without changing his orientation.
The second argument is the
duration
in real-time seconds.
It defaults to 5,
which is the value of
std.duration.
The third and fourth arguments are optional and ignored,
but if present they must be numbers.
The
accelTime
is
.5.
goto
behaves unpredictably when its first argument is a
Position
because of a bug in the member function
Observer::gotoLocation
in
version/src/celengine/obsever.cpp.
This member function never assigns any value
to the
traj
field (“trajectory”) of the
journey
data member of the C++
Observer
object.
A Celx workaround for this bug is to do a table-driven
goto
before the
goto
Object,
which will assign the value
Observer::Linear
to
traj.
A fix for this bug is in
the appendices that compile Celestia on Linux and Solaris.
If the first argument is an
Object,
the
goto
behaves like the g keystroke command.
The
Observer
goes straight towards (or away from) the center of the
Object
and halts at a certain distance from its center.
The halting distance depends on the
preferred distance
of that
type
of
Object,
defined in the C++ function
getPreferredDistance
in
version/src/celengine/observer.cpp.
For a planet, moon, or deep sky object,
the preferred distance is 5 times the radius.
For a city or other location,
it is 50 times the radius.
For a star, it is 100 times the radius.
The halting distance also depends on the
Observer’s
original distance from the
Object.
If he is far from the
Object
(more than 10 times the preferred distance),
he goes directly to the preferred distance.
Otherwise, he approaches 10 times closer to the object,
but no closer than
1.01
times its radius.
If he is less than or equal to
1.01
times the radius from the
Object’s
center
(e.g., if he is inside the
Milky Way),
the
goto
will move him
away
from the center to a point
1.01
times the radius way.
The
Observer
ends up facing the
Object.
His new up
Vector
lies in the plane common to his original up
Vector
and the
Vector
from his original
Position
to the center of the
Object.
This means that he must never
goto
an
Object
directly above or below him,
or at his current position,
on pain of division by zero.
The second argument of the
goto
is the
duration
in real-time seconds.
It defaults to 5,
which is the value of
std.duration.
The
accelTime
is
.5.
The third and fourth arguments are the
startInterpolation
and
endInterpolation.
They are optional and default to .25 and .75.
If they are outside the range 0 to 1 inclusive,
they are set to their default values rather than clamped to the range.
This form of
goto
may
setframe
the
Observer
to a different
Frame.
If his
Frame
is a lock frame,
it becomes the ecliptic frame of the
Object.
Otherwise, if his
Frame
is not the universal frame, the
Object
becomes the reference
Object
of his
Frame.
spock. He is intelligent but not experienced. His pattern indicates two-dimensional thinking.
kirk. Full stop.
sulu. Full stop, sir.
kirk. Z minus ten thousand meters. Stand by photon torpedoes.
Move the
Observer
in a straight line towards (or away from) the center of the
Object,
halting at the specified number of kilometers from the center.
If you want him to stay there,
he must already be
setframed
to a
Frame
whose reference
Object
is that
Object.
Upon arrival,
he will be facing the
Object.
This means that he must never go to a distance of zero,
on pain of division by zero.
The second argument is the distance in kilometers,
defaulting to 20000.
If the
Object’s
radius is greater than 20000 kilometers,
the
Observer
will end up inside the
Object.
The third argument is the duration of the
gotodistance
in real-time seconds.
It defaults to 5,
which is the value of
std.duration.
The fourth argument is the up
Vector
that the
Observer
will have upon arrival,
in universal coördinates.
This means that he must never go to an
Object
that lies in this direction from his starting
Position,
on pain of division by zero.
The
accelTime
is .5,
the
startInterpolation
is 0,
and the
endInterpolation
is .5.
See
Observer:goto
for these parameters.
The corresponding keystroke commands are
g,
Home,
and
End.
[Deprecated;
call
Observer:goto
instead.]
Move the
Observer
in a straight line to the
Position
in universal coördinates.
His orientation does not change.
The second argument is the number of seconds of real time the motion will take.
It defaults to 5, which is the value of
std.duration.
The
accelTime
is
.5; see
Observer:goto
for this parameter.
This method has the same
traj
bug as
Observer:gotosurface,
quod vide.
Move the
Observer
in a straight line to the
Position
at the given longitude, latitude, and distance from the given
Object.
If you want him to stay there,
he must already be
setframed
to the bodyfixed
Frame
for that
Object.
Upon arrival,
he will be facing the
Object.
This means that he must never go to a distance of zero,
on pain of division by zero.
The second and third arguments are the longitude and latitude
in radians and default to 0 and 0.
Longitude is measured to the east, latitude to the north.
Warning: the longitude and latitude are measured with respect to the
Object’s
bodyfixed
Frame.
But if the
Object
is a galaxy,
its bodyfixed
Frame
has no relation to the galaxy’s orientation.
See
alternativeBodyfixed.
The fourth argument is the distance in kilometers
and defaults to 5 times the
Object’s
radius.
The fifth argument is the number of seconds of real time the motion will take.
It defaults to 5, which is the value of
std.duration.
The sixth argument is the up
Vector
the
Observer
will have upon arrival,
in the
Object’s
bodyfixed frame.
It defaults to
(0, 1, 0),
so the north pole will be up when the
Object
is Earth,
and down when the
Object
is a retrograde rotator such as Venus.
The
Vector
must never point along the line connecting the center of the
Object
with the
Observer’s
new
Position,
on pain of division by zero.
The
accelTime
is
.5,
the
startInterpolation
is 0,
and the
startInterpolation
is .5;
see
Observer:goto
for these parameters.
The corresponding keystroke command is command-l (lowercase L)
on Macintosh.
Move the
Observer
in a straight line towards (or away from) the center of the
Object,
halting at a distance of 1.0001 times the
Object’s
radius from its center.
For the Earth, this would be about 600 meters above the surface.
The initial position of the
Observer
must not be at the center of the
Object,
on pain of division by zero.
The
Observer
is
setframed
to the
Object’s
bodyfixed
Frame.
It defaults to 5, which is the value of
std.duration.
This method never leaves the
Observer
looking towards the
Object.
If he is initially looking approximately towards the
Object
(i.e., if his initial direction of view is less than
90°
away from the center of the
Object),
he will end up looking horizontally towards the
Object’s
horizon
(i.e., 90°
from the center)
in the azimuth determined by his original up
Vector.
If the he is looking away from the
Object,
his orientation will be unchanged.
If the
Observer
is moving towards the
Object,
the limb (edge)
of the
Object
is not guaranteed to remain in the window as he descends to the surface.
For this,
we would have to update the
Observer’s
orientation in a tick handler
(tickHandler).
gotosurface
behaves unpredictably because of a
bug in the member function
Observer::gotoLocation
in
version/src/celengine/obsever.cpp.
This method never assigns the value
Observer::Linear
to the
traj
field (“trajectory”) of the
journey
data member of the C++
Observer
object.
A Celx workaround for this bug is to do a linear
goto
before the
gotosurface.
(The linear
goto
must not be the
goto
whose first argument is a
Position,
or the
gotolocation,
because they have the same bug.)
A fix for this bug is in
the appendices that compile Celestia on Linux and Solaris.
The corresponding keystroke command is control-g.
--Workaround to set the traj field to Linear before calling gotosurface. observer:goto({duration = 0}) --Now it's safe to go to the surface. observer:gotosurface(object, 5) wait(5) --Example: go to the point at the center of the sunlit hemisphere of the Earth. local sol = celestia:find("Sol") local earth = celestia:find("Sol/Earth") local lockFrame = celestia:newframe("lock", earth, sol) observer:setframe(lockFrame) local microlightyears = 5 * earth:radius() / KM_PER_MICROLY local position = celestia:newposition(microlightyears, 0, 0) observer:setposition(lockFrame:from(position)) observer:goto({duration = 0}) --Set the traj field to Linear. observer:lookat( lockFrame:from(std.position0), lockFrame:from(std.zaxis) ) --Settle slowly into the troposphere. observer:gotosurface(earth, 10) wait(10)
Return
true
if the
Observer
has not been deleted.
It is possible for any
Observer
except the active one to be deleted.
See also
Observer:splitview,
deleteview,
and
singleview.
If the
Observer’s
current
Frame
is the universal
Frame,
do nothing.
Otherwise,
adhere the
Observer
to a lock
Frame
(lockFrame).
The
Frame’s
reference
Object
is that of his current
Frame,
and its target
Object
is the argument of the method.
If the reference and target
are the same
Object,
the target
Object
is replaced by the star of its solar system.
The corresponding keystroke command is
:
(colon).
Orient the
Observer
to look at the given target
Position,
with the given up
Vector
appearing to point upwards.
In other words,
orient him so that
Vector
points from his current
Position
towards the given target
Position.Vector
lies in the plane common to his new forward
Vector
and the given up
Vector,
and is less than
90°
from the given up
Vector.
The given target
Position
and the given up
Vector
are in universal coördinates,
even if the
Observer
has been
setframed
to a different
Frame
of reference.
The given target
Position
cannot be the
Observer’s
Position.
The given up
Vector
does not have to be of length 1,
but it cannot be of length zero.
The given up
Vector
cannot be parallel to the one
from the
Observer’s
Position
to the given target
Position.
Violation of these rules results in division by zero and unpredictable
behavior;
see
direction.
The optional third-from-last argument of
Observer:lookat
is the source
Position.
When the source
Position
is absent, the
Observer
looks directly at the target
Position.
When the source
Position
is present,
he looks along a
Vector
parallel to the one from the source
Position
to the target
Position.
See the parallax example in
parallax.
Other methods that change the orientation of an
Observer
are
Observer:goto,
Observer:gotodistance,
Observer:gotolonglat,
Observer:gotosurface,
Observer:orbit,
Observer:rotate,
Observer:setorientation,
and
Observer:track.
See also
Position:orientationto
and
glu.LookAt.
The keystroke command * (asterisk)
makes the
Observer
look in the opposite direction without changing his up
Vector.
Make the
Observer
the active
Observer,
and his view the active view.
For the definition of the active
Observer,
see class
Observer.
The corresponding keystroke command is
tab.
An
Observer
can also be made active by clicking on his view.
See also
Observer:splitview
and
Observer:singleview.
Orbit the
Observer
around an axis that goes through the center of the reference
Object
of the
Frame
to which he has been
setframed.
If that
Frame
has no reference
Object
(i.e., if it is the universal
Frame),
do nothing.
The argument is a
Rotation
whose axis is in the coördinates of the
Observer’s
personal frame of reference.
(See
overviewFrames
for this frame.
Its X axis always points towards his right;
its Y axis towards his zenith.)
The axis of the orbit is parallel to the axis of the
Rotation;
the angular length of the orbit is the angle of the
Rotation.
The orbit is instantaneous.
The
Observer
changes his orientation during the
orbit
by performing the same
Rotation.
For example, if he is facing the center
(or the horizon) of the reference
Object
before the
orbit,
he will still be facing the center
(or the horizon)
afterwards.
See the examples in
orbitObserver.
The corresponding keystroke command is C.
Rotate the
Observer,
changing his orientation but not his
Position.
The argument is a
Rotation
whose axis is in universal coördinates,
even if the
Observer
has been
setframed
to a different
Frame
of reference.
The rotation is instantaneous.
See
rotateObserver
for an example.
The corresponding keystroke commands are the four arrow keys
and the * (asterisk).
Other methods that change the orientation of an
Observer
without changing his
Position
are
Observer:lookat,
Observer:setorientation,
and the
Observer:goto
whose first argument is a table.
Set the
Observer’s
vertical field of view.
The argument is an angle in radians.
A small angle zooms in for magnified, telescopic view;
a big angle yields zooms out for a wide field of view.
The method will be ignored if the angle is smaller than
.001° = 3.6″
or bigger than
120°.
Since the argument is converted from
double
to
float,
the exact cutoffs in degrees are slightly farther apart.
They are
4,611,686,001,928,850
253
·
2–9
≈
.0009999999964224498
and
8,444,249,536,302,325
253
·
27
≈
120.000003339304
Suppose we have a Celestia window whose height in pixels is h, and a user whose distance in pixels from the window is d. The user is on a line that is perpendicular to the plane of the window and that goes through the center of the window. From the user’s point of view, the window spans a vertical field of view of θ radians. Then the following relations hold. h = 2dtan θ 2 d = h / 2 tan (θ / 2) θ = 2 arctan h / 2 d
The corresponding keystroke commands are
.
(period to zoom out)
and
,
(comma to zoom in).
The field of view is set by
Celestia:sane
to the field that a user would have
at a distance of 400 millimeters from the window.
The field of view is also changed by
Observer:splitview.
See also
Celestia:getscreendimension
and the following methods of class
Observer:
getfov,
gethorizontalfov,
sethorizontalfov,
getverticalfov,
setverticalfov,
getmagnification,
and
setmagnification.
See also
std.gethorizontalfov
and
std.getverticalfov.
Adhere the
Observer
to the given
Frame
of reference.
This causes him to remain in the same
Position
and
orientation
with respect to the
Frame,
unless disturbed by a keystroke command or a Celx method call.
If an
Observer
is adhered to a
Frame
that moves or rotates,
he will move or rotate with it.
Before the first call to
setframe,
the original
Observer
adheres to the universal
Frame.
You probably want to call
setframe
before setting the
Observer’s position
or orientation with respect to a celestial
Object;
an example is in
eclipticFrame.
The
Observer’s
frame is also set by
Observer:chase,
Observer:gotosurface,
Observer:lock,
and
Observer:synchronous.
See also
Observer:getframe.
Set the
Observer’s
horizontal field of view to the given angle in radians.
This method works correctly only if the window is not
splitviewed.
The method is ignored if it would result in a vertical field of view
smaller than
.001° = 3.6″
or greater than
120°.
The field of view is set by
Celestia:sane
to the field that a user would have
at a distance of 400 millimeters from the window.
See also
Observer:setfov
and
Observer:gethorizontalfov.
Set the types of locations that will be labelled
for this
Observer.
The argument is a table whose values are
booleans
and whose keys are mostly in Latin:
astrum (star),
catena (chain),
chaos,
chasma (hole),
city,
corona (oval),
crater,
dorsum (ridge),
farrum (pancake),
fluctus (outflow),
fossa (depression),
insula (island),
landingsite,
linea (line),
mare (sea),
mensa (mesa),
mons (mountain),
observatory,
other (miscellaneous),
patera (bowl),
planitia (low plain),
planum (high plain),
regio (region),
reticulum (netlike pattern),
rima (fissure),
rupes (scarp),
terra (land),
tessera (complex ridges),
tholus (dome),
undae (dunes),
vallis (valley),
volcano.
These names appear as the value of the
featureType
field of the info table of a location;
see
Object:getinfo.
The
Font
of a label is the
LabelFont
in
celestia.cfg,
which defaults to the
Font
in
celestia.cfg,
which defaults to
default.txf.
Warning:
Celestia:sane
turns all the location flags on,
but it turns the
locations
field of the label flags off.
See also
Observer:getlocationflags.
Set the
Observer’s
magnification.
See
Magnification.
The default magnification is 1.
If the magnification is doubled,
the diameter of the field of view is halved.
The magnification is displayed in the lower right corner of the Celestia window.
See also
Observer:getmagnification
and
Observer:setfov.
Set the
Observer’s
orientation.
See
setOrientation.
The argument is the
Rotation
which,
when applied to the initial orientation,
would produce the desired orientation.
The initial orientation faces towards
z = –∞,
with
y = ∞
overhead.
The axis of the
Rotation
argument is always in universal coördinates,
even if the
Observer
has been
setframed
to another
Frame.
You probably want to call
setframe
before
setorientation.
Celestia:sane
sets the active
Observer’s
orientation to
std.orientation0.
See also
Observer:getorientation,
Observer:goto,
Observer:lookat,
and
Observer:rotate.
Set the
Observer’s
Position;
see
observerSetposition.
The
Position
is in universal coördinates even if the
Observer
has been
setframed
to a different
Frame.
You probably want to call
setframe
before
setposition.
Celestia:sane
sets the active
Observer’s
Position
to
std.position0.
See also
Observer:getposition
and
Observer:goto.
Set the
Observer’s
speed in microlightyears per second of real time
with respect to the
Frame
to which he has been
setframed.
If the argument is positive,
his direction of motion is along his forward
Vector,
and vice versa.
This method does not set the
Observer’s
travelling
bit.
The corresponding keystroke commands are
a,
z,
q,
s,
x,
and the function keys F1 through F7.
See also
Observer:getspeed
and
Celestia:setoverlayelements.
--[[
Move the observer backward, displaying his position in microlightyears along the
Z axis. Since his forward vector is (0, 0, -1) and his speed is negative, he
will move away from the origin along the positive Z axis. The Sun and planets
will recede towards the center of the window.
We must use Celestia:getscripttime, since Celestia:getsystemtime is updated only
once per second.
]]
require("std")
--variables used by tickHandler:
local observer = celestia:sane()
local t0 = nil
local function tickHandler()
local s = string.format(
"x = %.1f microlightyears\n" --1 digit to right of decimal point
.. "t = %.1f real-time seconds",
observer:getposition():getz(),
celestia:getscripttime() - t0)
celestia:print(s)
end
local function main()
observer:setposition(std.position0)
t0 = celestia:getscripttime()
observer:setspeed(-1) --1 microlightyear per real-time second
celestia:registereventhandler("tick", tickHandler)
end
main()
Set the texture files to be painted on the surface of a celestial
Object.
The default files are the ones specified in the
Object’s
Texture
parameter in a
.ssc
file,
but the
.ssc
file can also specify an
AltSurface.
The argument of
Observer:setsurface
is the string which is the first parameter of the
AltSurface,
or the empty string
""
to go back to the default files.
A default surface may include regions filled in by artwork,
but a “limit of knowledge” surface is restricted
to features that have actually been photographed.
The corresponding keystroke command is
+
(plus).
See also
Observer:getsurface.
Set the
Observer’s
vertical field of view to the given angle in radians.
This method does the same thing as
Observer:setfov,
except that
Observer:setverticalfov
works correctly only if the window is not
splitviewed.
The field of view is set by
Celestia:sane
to the field that a user would have
at a distance of 400 millimeters from the window.
See also
Observer:getverticalfov.
Make this
Observer
the active
Observer.
Delete all other
Observers
and their views.
This method is called by
Celestia:sane.
The corresponding keystroke command is
control-d.
See also
Observer:makeactiveview.
Divide the
Observer’s
view into two subviews,
shrinking the existing view to make room for the new one.
See
Iapetus
and
Splitview.
If the first argument is
"h"
(case insensitive),
the existing view is divided horizontally
and the new view appears above it.
Any other string divides the existing view vertically
and the new view appears to its right.
The corresponding keystroke commands are
control-r
for horizontal split,
control-u
for vertical.
If the existing view was the active view,
it remains active after the split.
The second argument specifies what fraction of the area of the existing view
is retained by that view.
For example, the arguments
"h"
and
1/3
will reduce the existing view to one third of its original area,
and the new view will occupy the upper two thirds.
The argument is clamped to the range .1 to .9,
and defaults to .5.
If the Celx Standard Library has been included with
require("std"),
Observer:splitview
returns the new
Observer.
Otherwise, it returns
nil.
The new
Observer
inherits the attributes of the active
Observer:
his position, orientation, etc.
(Note that the active
Observer
is not necessarily the one that was split.)
The new
Observer
is appended to the array of
Observers
returned by
celestia:getobservers,
and the message
“Added view”
is
flashed
in the window.
See also the
deleteview,
singleview,
makeactiveview,
and
gettime
methods of class
Observer,
and the
synchronizetime,
istimesynchronized,
and
setwindowbordersvisible
methods of class
Celestia.
Adhere the
Observer
to the
Object’s
bodyfixed
Frame.
This method has no effect unless the
Object
has a body, or is a star or location.
The corresponding keystroke command is y.
Keep the
Observer
aimed at the designated
Object,
i.e.,
keep his forward
Vector
pointing towards the
Object.
This method automatically executes the equivalent of the following code
with every tick of the simulation.
The
Observer
must therefore never be at the
Position
of the tracked
Object,
and the tracked
Object
must never be directly above the
Observer,
on pain of division by zero.
Note that
track
can allow the
Observer’s
up
Vector
to wander;
see the example in
clouds.
The argument
nil
turns off tracking.
Celestia:sane
turns off tracking.
The corresponding keystroke command is
t.
See also
Observer:gettrackedobject.
Return
true
if this
Observer
is executing a
goto,
gotodistance,
gotolocation,
gotolonglat,
gotosurface,
center,
or
centerorbit.
(This method pays no attention to
Observer:setspeed.)
It also returns
true
if the user is executing a travelling keystroke command such as
c, g, shift-c, or control-g.
“Travelling”
has a double L.
The travelling bit is displayed only when it is set,
in the lower right corner of the Celestia window.
See also
Observer:cancelgoto.
A solar system
Object
is a celestial
Object
described in an
.ssc
(Solar System Catalog)
file.
A
Phase
represents a segment of the lifespan of a solar system
Object.
The methods of the
Phase
retrieve information from the
.ssc
file.
For example,
the phases of the spacecrafts
Cassini
and
Huygens
are listed in the
Timeline
sections of the file
extras-standard/cassini/cassini.ssc.
If the
Object
has no
Timeline,
its lifespan consists of a single
Phase.
The above example is in
phases.
Class
Phase
is implemented in
version/src/celestia/celx_phase.cpp.
and
version/src/celengine/timelinephase.cpp.
Return the
Frame
with respect to which the
Object’s
orientation is defined in the .ssc file.
See also
Phase:getorientation
and
Object:bodyframe.
The
getcoordinatesystem
method of the
Frame
returns the string
"invalid".
See that method for an explanation and workaround.
Return the solar system
Object’s
orientation at TDB time
t
with respect to the frame returned by
Phase:bodyframe.
t
is clamped to the
Phase’s timespan.
This means that if
t
is before the
Phase’s
starting time,
it is set to the starting time.
If
t
is after the
Phase’s
ending time,
it is set to the ending time.
The return value is a
Rotation
object.
A solar system
Object
has no
getorientation
method,
but its orientation can be deduced from the axes of its bodyfixed frame.
The orientation returned by
Phase:getorientation
is the same as the orientation deduced from the axes of the
Object’s
bodyfixed frame,
except for a
180°
rotation around the Y axis.
For another examples of this
180°
rotation around the Y axis, see
alternativeBodyfixed
and
scriptedRotation.
Return the
Frame
with respect to which the
Object’s
orbit is defined in the
.ssc
file.
See also
Object:orbitframe.
The
getcoordinatesystem
method of the
Frame
returns the string
"invalid".
See that method for an explanation and workaround.
Return the solar system
object’s
position at TDB time
t
with respect to the
Frame
returned by
Phase:orbitframe.
t
is clamped to the
Phase’s
timespan, as in
Phase:getorientation.
Warning: in a
.ssc
or a
.xyzv
file,
the first coördinate is the Celx
x
coördinate of the solar system object with respect to the frame.
The second coördinate is the negative of the Celx z
coördinate.
The third coördinate is the Celx y
coördinate.
The same inversion appears in the return values
of the scripted orbit methods in
scriptedOrbit.
See also
Object:getposition.
Return the starting and ending times of this
Phase
as TDB numbers.
If there is a
Phase
after this one, it begins at the same time that this one ends.
In that case,
Object:getposition
believes that common point in time belongs to the
Phase
after this one.
The starting time of a
Phase
may be
-math.huge
(i.e., –∞),
and the ending time may be
math.huge
(i.e., ∞).
To print UTC times that agree with those in the
.ssc
file, we have to use
Celestia:fromjulianday
instead of
Celestia:tdbtoutc.
A
Position
is a point with Cartesian
(x, y, z)
coördinates measured in microlightyears
with respect to a frame of reference.
See
position
for
Positions,
lightyear
for microlightyears,
and
framesOfReference
for
Frames.
The
Position
object specifies the coördinates but not the
Frame.
Each coördinate
is a 128-bit fixed point number;
see
positionCoordinates
for the peculiarities of this format.
For example, the range of a
Position
coördinate
(–263
to
263
–
2–64
inclusive)
is much smaller than the range of a
Vector
coördinate
(approximately
–21024
to
21024,
not counting the denormalized values),
but within this range a
Position
coördinate has much more precision.
Class
Position
is implemented in
version/src/celestia/celx_position.cpp,
version/src/celengine/univcoord.cpp,
and
version/src/celutil/bigfix.cpp.
Create a
Position
from Cartesian coördinates.
Create a
Position
from spherical coördinates.
Get an existing
Position
at TDB time
t,
defaulting to the current simulation time.
Make an exact copy of a
Position.
Position:getx
etc., would cause a loss of precision.
The methods
Position:getx, etc.,
give read-only access to the fields.
Loop through the names of the fields of a
Position
in the order
"x",
"y",
"z".
Position
addition, subtraction, and negation (unary minus).
It’s surprising that we can add two
Positions;
the Celx Standard Library exploits this in the implementation of
Position:getbinary.
Multiplication and division. The resulting values have only the precision of a normal Celx number, not a 128-bit fixed point number.
local position2 = n * position1 --(Added) n is a number local position2 = position1 * n --(Added) same as above local position2 = position1 / n --(Added) n must be a nonzero numberRotation and conversion. Conversion may perform translation as well as rotation.
--Rotate a Position around the origin. local position2 = rotation:transform(position1) --Convert the Position from the universal Frame to this Frame. local position2 = frame:from(position1) --Convert the Position from this Frame to the universal Frame. local position2 = frame:to(position1)std.position0
=
(0, 0, 0)std.position
=
(0, 0, 1).
An
Observer
at this
Position
in the universal frame,
in the initial orientation
(facing towards
Taurus/Gemini)
will see a reassuring view of the Sun from a safe distance.
std.position1
=
(–1,
1 − 2–64,
–(2–64)).
For testing purposes.
The
x
coördinate has an integer of all ones
and a fraction of all zeroes.
y
has an integer of all zeroes and a fraction of all ones.
z
has an integer of all ones and a fraction of all ones.
Return the sum of a
Position
and
a
Vector.
Return the distance in kilometers between two
Positions.
Their order does not matter.
Return a table containing the altazimuth spherical coördinates of the
Position:
the
altitude
and
azimuth
in radians,
and the
distance
in microlightyears.
The XZ plane is the horizon. The X axis points east and the Z axis points south, except for the following two cases. If the origin (0, 0, 0) is at the north pole, the X axis points along the meridian of 90° East, and the the Z axis points along the meridian of 0° East. If the origin is at the south pole, the X axis points along the meridian of 90° East, and the the Z axis points along the meridian of 180° East.
The
altitude
is in the range
–π/2
to
π/2
inclusive,
measured up or down from the XZ plane.
The
azimuth
is in the range 0 (inclusive) to
2π
(exclusive)
measured in the XZ plane
clockwise from the negative Z axis (the north point on the horizon).
Don’t call this method for a
Position
in a chase or lock
Frame,
since these
Frames
measure their azimuth in the XY plane.
The altitude and azimuth are zero if
x,
y,
z
are all zero.
The azimuth is zero if
x
and
z
are zero.
In neither case does
Position:getaltaz
call the Lua function
math.atan2.
We avoid the call because
the call to the underlying C++ function
atan2
with two zero arguments would set the “error number” variable
errno
on some platforms.
Don’t call this method for a
Position
in a chase or lock
Frame,
which measure their azimuth (longitude) in the XY plane.
For the workaround, see
Positon:getlonglat.
See also
Celestia:newpositionaltaz,
Position:getlonglat,
and
Vector:getaltaz.
Return a table showing the value of the
Position
as three strings of 128
"1"s
and
"0"s.
The most significant byte is on the left.
The most significant bit within each byte is on the left.
Return a table showing the value of the
Position
as three strings holding decimal numbers.
These strings show the exact 128-bit values of the coördinates.
The methods
Position:getx,
etc., show only a 64-bit approximation.
The
x
coördinate of the above
Position
holds
22,773,757,910,726,981,404,533,546,592,213,819,164
·
2–64
=
1234567890123456789.12345678901234567888776927357952217789716087281703948974609375
which is as close as a 128-bit fixed point number can get to
1234567890123456789.1234567890123456789.
The above call to
Position:getx
returns
4,822,530,820,794,753
253
·
261
=
1,234,567,890,123,456,768
which is as close as a 64-bit floating point number can get to
1234567890123456789.1234567890123456789.
Return a table showing the value of the
Position
as three strings of 32 uppercase hexadecimal digits.
The most significant byte is on the left.
The most significant nibble within each byte is on the left.
Return a table containing the spherical coördinates of the
Position:
the
latitude
and
longitude
in radians,
and the
distance
in microlightyears.
The
latitude
is in the range
–π/2
to
π/2
inclusive,
measured up and down from the XZ plane.
The
longitude
is in the range 0 (inclusive) to
2π (exclusive),
measured in the XZ plane
counterclockwise from the positive X axis.
Don’t call this method for a
Position
in a chase or lock
Frame,
which measure their longitude in the XY plane.
The workaround is shown below and in
Lagrangian.
The longitude and latitude are zero if
x,
y,
z
are all zero.
The longitude is zero if
x
and
z
are zero.
In neither case does
Position:getlonglat
call the Lua function
math.atan2.
We avoid the call because
the call to the underlying C++ function
atan2
with two zero arguments would set the “error number” variable
errno
on some platforms.
See also
Celestia:newpositionlonglat,
Position:getaltaz,
and
Vector:getlonglat.
Return a table containing each coördinate of the
Position
encoded as a string
that can be passed to
Celestia:newposition
or that can be used in a
cel:
URL.
See
bits128.
Return the x coördinate of a
Position.
Since this method returns a Celx number
(doubleArithmetic),
it gives only an approximation of the value.
For the true value, call
Position:getbinary,
Position:getdecimal,
Position:gethex,
or
Position:geturl.
To loop through the names of the three Cartesian coördinates,
see
std.xyz.
For the values of the spherical coördinates,
see
Position:getlonglat
or
Position:getaltaz.
See also
Position:gety,
Position:getz,
and
Position:getxyz.
Return a list of the coördinates of a
Position.
Warning: if the return value is passed as an argument to
string.format
(or to any other function),
it must be the
last
argument.
See also
Position:getx,
Position:gety,
Position:getz,
and
Vector:getxyz.
Return the y coördinate of a
Position.
Since this method returns a Celx number
(doubleArithmetic),
it gives only an approximation of the value.
For the true value, call
Position:getbinary,
Position:getdecimal,
Position:gethex,
or
Position:geturl.
To loop through the names of the three Cartesian coördinates,
see
std.xyz.
For the values of the spherical coördinates,
see
Position:getlonglat
or
Position:getaltaz.
See also
Position:getx,
Position:getz,
and
Position:getxyz.
Return the z coördinate of a
Position.
Since this method returns a Celx number
(doubleArithmetic),
it gives only an approximation of the value.
For the true value, call
Position:getbinary,
Position:getdecimal,
Position:gethex,
or
Position:geturl.
To loop through the names of the three Cartesian coördinates,
see
std.xyz.
For the values of the spherical coördinates,
see
Position:getlonglat
or
Position:getaltaz.
See also
Position:getx,
Position:gety,
and
Position:getxyz.
Return the orientation that would make an
Observer
at the
sourcePosition
face towards the
targetPosition,
with the
upVector
pointing up.
The orientation is a
Rotation
object.
The
sourcePosition
and
targetPosition
must have different values.
The
upVector
must be nonzero and must not be parallel to the line connecting the
Positions.
Observer:lookat
does the same thing,
except that it gives the orientation to the
Observer
instead of returning it.
Return a
Vector
containing the same coördinates as the
Position,
subject to the loss of precision as the 128-bit fixed point values
are converted to Celx numbers.
Return the
Vector
that points from
position1
to
position2.
An object of this class represents an orientation, rotation, or quaternion. Celx makes no distinction between these types of things. See orientation.
An orientation determines, and is determined by, a forward
Vector
and an up
Vector.
They define the direction in which the orientation is facing
and the direction that the orientation thinks is up.
For example, the initial orientation of the initial
Observer
(a.k.a.
std.orientation0)
faces towards the summer solstice in
Taurus/Gemini,
with the north pole of the ecliptic in
Draco
overhead.
Its forward
Vector
is
(0, 0, –1)
(a.k.a.
std.forward)
and its up
Vector
is
(0, 1, 0)
(a.k.a.
std.up)
in the universal frame.
The forward and up
Vectors
of an orientation are returned by
Rotation:getforwardup,
and an orientation can be created from these vectors by
Celestia:newrotationforwardup.
A
Rotation
determines, and is determined by, and axis and an angle.
The axis of a nonzero
Rotation
is returned by
Rotation:imag
and is the
Vector
formed by the
x,
y,
z
fields of the
Rotation.
The angle of a
Rotation
must be in the range
0°
to
360°
inclusive.
The angle may be derived from
Rotation:real
or from the value of the
w
field.
A new
Rotation
can be created from an axis and an angle by
Celestia:newrotation.
See also
Rotation:setaxisangle.
In Celx,
an orientation is identical to the
Rotation
that would get us to that orientation from the initial orientation.
For example,
std.orientation0
is identical to
std.rotation0,
which is the
Rotation
whose angle is
0°
and whose axis is irrelevant.
A quaternion determines, and is determined by,
its coördinates
w,
x,
y,
z.
The coördinates are available as the fields of the quaternion,
and are also returned by
Rotation:real
and
Rotation:imag.
A quaternion can be created from the coördinates
by the four-argument
Celestia:newrotation.
To represent an orientation or rotation,
a quaternion must be a unit quaternion,
satisfying
w2 +
x2 +
y2 +
z2 = 1
To create a unit quaternion,
the arguments of the four-argument version of
Celestia:newrotation
must satisfy the above relationship,
and the
Vector
argument of
Celestia:newrotation
and
Rotation:setaxisangle
must be a unit
Vector.
Three warnings.
Unit quaternions can be added with the
+
operator,
but the sum will not be a unit quaternion.
A unit quaternion can be multiplied by any number,
but if the number is other than 1,
the result will not be a unit quaternion.
A unit quaternion
can be multiplied by any
Vector,
but if the
Vector
is not a unit
Vector,
the product will not be a unit quaternion.
In Celx, a unit quaternion is identical to the
Rotation
whose axis is the
Vector
(x, y, z)
and whose angle is
2 arccos w.
Class
Rotation
is implemented in
version/src/celestia/celx_rotation.cpp
and
version/src/celmath/quaternion.h
with the template argument
T = double.
An
Object
needs no
getorientation
method
(but see
Phase:getorientation)
because
we can get the
Object’s
orientation in the universal
Frame
at time
t
as follows.
The right operand of the
^
operator must be
–1.
As a mathematical curiosity,
Celx permits the multiplication of a unit
Vector
and a
Rotation.
The unit
Vector
acts as a
Rotation
whose imaginary part is the unit
Vector,
and whose real part is
0 = cos
π
2
This is a
Rotation
of
π
radians or
180°
around the unit
Vector.
Therefore the following multiplications do the same thing.
std.rotation0 =
celestia:newrotation(std.xaxis, 0)
Rotation
of
0°
around an irrelevant axis.
std.orientation0 =
std.rotation0.
Observer.
std.radecRotation =
celestia:newrotation(std.xaxis, std.tilt)
Return the same
Rotation,
but in the opposite direction.
This method negates the axis of the
Rotation.
(It can’t negate the angle,
since the angle of a
Rotation
is always nonnegative.)
Return the forward and up
Vectors
of the orientation that is identical to this
Rotation.
To convert the
Vectors
back into a
Rotation,
call
Celestia:newrotationforwardup.
Return the imaginary part of the
Rotation.
If the angle of the
Rotation
is
0°
or
360°
(i.e., if the real part of the
Rotation
is 1 or
–1
respectively),
the imaginary part is the
Vector
(0, 0, 0).
Otherwise, the imaginary part is a
Vector
giving the axis of the
Rotation.
The length of the
Vector
is the sine of half of the angle of the
Rotation.
Warning:
the return value of
Rotation:imag
is not equal to the vector argument of
Celestia:newrotation
or
Rotation:setaxisangle.
See also
Rotation:real.
Return the real part of the
Rotation,
in the range
–1
to 1 inclusive.
The value of the real part is the cosine of half of the angle of the
Rotation.
See also
See also
Rotation:imag.
Warning:
the return value of
Rotation:real
is not equal to the angle argument of
Celestia:newrotation
or
Rotation:setaxisangle.
Set the axis and the angle of the
Rotation.
The axis must be a unit
Vector.
The angle is in radians and must be in the range 0 to
2π
inclusive.
This method pays attention only to the cosine of the angle,
not the value of the angle,
so
–1°
would be treated as
1°,
and
361°
would be treated as
359°.
See what I mean about staying in the range 0 to
2π
inclusive?
See also
Celestia:newrotation.
Return the
spherical linear interpolation
of two
Rotations;
see
setOrientation.
n
must be a number in the range 0 to 1 inclusive.
If n is 0,
the return value is
rotation0.
If n is 1,
the return value is
rotation1.
If n is between 0 and 1,
the return value is a weighted average of
rotation0
and
rotation1.
This method is implemented by the member function
Quaternion<T>::slerp
in
version/src/celmath/quaternion.h.
Rotate a
Vector
or a
Position
around the origin.
(If the Celx Standard Library has not been
required,
the argument can only be a
Vector.)
For a
transform
that changes the direction in which a
Vector
is pointing, see
transformVector
(simple)
and
Quasar
(complicated).
For a
transform
that changes the frame of reference in which the coördinates of a
Position
are written, see the big example below.
See also
Frame:from
and
Frame:to.
A
Texture
represents an image file.
See
opengl
for the series of function calls that will display it.
See also
Object:preloadtexture,
Observer:setsurface,
and the OpenGL functions
gl.TexCoord
and
gl.TexParameter.
Class
Texture
is implemented in
version/src/celestia/celx.cpp.
This method must be called before
gl.TexCoord;
see
opengl
for an example.
It calls the OpenGL function
glBindTexture
with the argument
GL_TEXTURE_2D.
Return the height of the
Texture
in pixels.
The return value is an integer.
You will probably use this value as an argument of
gl.Vertex;
see
opengl
for an example.
See also
Texture:getwidth
and
gl.TexCoord.
Return the width of the
Texture
in pixels.
The return value is an integer.
You will probably use this value as an argument of
gl.Vertex;
see
opengl
for an example.
See also
Texture:getheight
and
gl.TexCoord.
A
Vector
is an invisible, straight arrow extending from the origin
(0, 0, 0)
to the point whose
(x, y, z)
coördinates are in the
Vector.
(A
Position
has the same three coördinates,
but with a much greater precision.
See
positionCoordinates.)
The
coördinates are measured in
microlightyears with respect to a
Frame
of reference.
If the
length
of the
Vector
is greater than zero, the
Vector
points in some direction.
See
vectors.
Class
Vector
is implemented in
version/src/celestia/celx_vector.cpp
and
version/src/celmath/vecmath.cpp
with the template argument
T = double.
Create a
Vector
from Cartesian coördinates.
Create a
Vector
from spherical coördinates.
The methods
Vector:getx, etc.,
give read-only access to the fields.
Loop through the names of the fields of a
Vector
in the order
"x",
"y",
"z".
Vector
addition, subtraction, and negation (unary minus):
Multiplication (by a scalar), dot product, and cross product:
local vector2 = n * vector1 --n is a number local vector2 = vector1 * n --n is a number local n = vector1 * vector2 --dot product of two vectors, n is a number local vector3 = vector1 ^ vector2 --cross product of two vectors
As a mathematical curiosity,
Celx permits the multiplication of a unit
Vector
and a
Rotation.
Think of the unit
Vector
as a
Rotation
whose imaginary part is the unit
Vector,
and whose real part is
0 = cos
π
2
This is a
Rotation
of
π
radians or 180° around the unit
Vector.
Therefore the following multiplications do the same thing.
Division:
local vector2 = vector1 / n --(Added) n is a nonzero number local vector2 = vector1 * (1 / n) --workaround if not using Celx Standard LibRotation and conversion. Conversion may perform translation as well as rotation.
--Rotate the Vector around the origin. local vector2 = rotation:transform(vector1) --Convert the Vector from the universal Frame to this Frame. local vector2 = frame:to(vector1) --Convert the Vector from this Frame to the universal Frame. local vector2 = frame:from(vector1)
A
Rotation
is determined by an axis and an angle.
The axis is a
Vector.
An orientation
is determined by its forward and up
Vectors.
In Celx, an orientation is a
Rotation.
std.forward
and
std.up
are the forward and up vectors of the initial orientation of the initial
Observer.
In the universal
Frame,
they point towards the
summer solstice
in
Taurus/Gemini
and the north pole of the
ecliptic
in
Draco,
respectively.
See
Celestia:newrotationforwardup
and
Rotation:getforwardup.
std.xaxis = (1, 0, 0)std.yaxis = (0, 1, 0)std.zaxis = (0, 0, 1)std.forward = (0, 0, –1)std.up = (0, 1, 0)
Return the angle in radians between two nonzero
Vectors.
See
dotProduct.
The returned angle is
in the range 0 to
π
inclusive.
If you need a wider range,
call
math.atan2
(–π
to
π
inclusive),
or get a longitude from
Position:getlonglat
or
Vector:getlonglat
(0 [inclusive] to
2π
[exclusive]).
Return a unit
Vector
vector3
satisfying three requirements:
vector3
lies in the same plane as
vector1
and
vector2.vector3
is perpendicular to
vector1vector3
is less than
90°
away from
vector2.
vector1
and
will usually be the forward
Vector
of an orientation,
and
vector2
will determine the up
Vector.
vector1
and
vector2
must define a plane.
In other words,
both must be nonzero
and they cannot be colinear.
Return a table containing the altazimuth spherical coördinates of the
Vector:
the
altitude
and
azimuth
in radians,
and the
distance
in microlightyears.
The XZ plane is the horizon. The X axis points east and the Z axis points south, except for the following two cases. If the origin (0, 0, 0) is at the north pole, the X axis points along the meridian of 90° East, and the the Z axis points along the meridian of 0° East. If the origin is at the south pole, the X axis points along the meridian of 90° East, and the the Z axis points along the meridian of 180° East.
The
altitude
is in the range
–π/2
to
π/2
inclusive, measured up and down from the XZ plane.
The
azimuth
is in the range 0 (inclusive)
to
2π
(exclusive), measured in the XZ plane
clockwise from the
–Z
axis,
which points towards the north point on the horizon.
The altitude and azimuth are zero if
x,
y,
z
are all zero.
The azimuth is zero if
x
and
z
are zero.
In these cases
Vector:getaltaz
does not call the Lua function
math.atan2.
We avoid the call because passing a pair of zero arguments
to the underlying C++ function
atan2
would set the “error number” variable
errno
on some platforms.
See also
Celestia:newvectoraltaz,
Vector:getlonglat,
and
Position:getaltaz.
Return a table containing the spherical coördinates of the
Vector:
the
latitude
and
longitude
in radians,
and the
distance
in microlightyears.
The
latitude
is in the range
–π/2
to
π/2
inclusive, measured up and down from the XZ plane.
The
longitude
is in the range 0 (inclusive) to
2π
(exclusive),
measured in the XZ plane
counterclockwise from the positive X axis.
Don’t call this method for a
Vector
in a chase or lock frame,
since these frames measure their longitude in the XY plane.
The workaround is shown below.
The latitude is zero if
x,
y,
z
are all zero.
The longitude is zero if
x
and
z
are zero.
In these cases
Vector:getlonglat
does not call the Lua function
math.atan2.
We avoid the call because passing a pair of zero arguments
to the underlying C++ function
atan2
would set the “error number” variable
errno
on some platforms.
See also
Celestia:newvectorlonglat,
Vector:getaltaz,
and
Positionector:getlonglat.
Return the
x
coördinate of a
Vector.
To loop through the names of the three Cartesian coördinates,
see
std.xyz.
For the values of the spherical coördinates,
see
Vector:getlonglat
or
Vector:getaltaz.
See also
Vector:gety,
Vector:getz,
and
Vector:getxyz.
Return a list of the coördinates of a
Vector.
Warning: if the return value is passed as an argument to
string.format
(or to any other function),
it must be the
last
argument.
See also
Vector:getx,
Vector:gety,
Vector:getz,
and
Position:getxyz.
Return the y
coördinate of a
Vector.
To loop through the names of the three Cartesian coördinates,
see
std.xyz.
For the values of the spherical coördinates,
see
Vector:getlonglat
or
Vector:getaltaz.
See also
Vector:getx,
Vector:getz,
and
Vector:getxyz.
Return the z
coördinate of a
Vector.
To loop through the names of the three Cartesian coördinates,
see
std.xyz.
For the values of the spherical coördinates,
see
Vector:getlonglat
or
Vector:getaltaz.
See also
Vector:getx,
Vector:gety,
and
Vector:getxyz.
Return the length of the
Vector,
always nonnegative.
Warning: the length method of a Lua
string
is named
len.
The smallest positive number whose square is positive is
2
·
2–538,
assuming our standard 53-bit mantissa.
If the absolute value of every coördinate is
less than this value,
the return value of
length
will be zero and it will be impossible to
normalize
the
Vector.
See
distancePositions.
Return a
unit
Vector
(a
Vector
whose length is 1)
pointing in the same direction as the given
Vector.
See
distancePositions.
If the
length
method of the
Vector
would return zero,
the
Vector
does not point in any direction and the
normalize
method will divide by zero.
The division happens when the C++ function
vector_normalize
in
version/src/celestia/celx_vector.cpp
calls the C++ member function
Vector3<T>::normalize
in
version/src/celmath/vecmath.h.
The result is machine dependent and
is usually a vector of three
“not a numbers” or three “infinities”.
The .408248290463863 ≈ 1 6 is the value of each coördinate of the unit vector pointing along the diagonal of a cube.
Return a
Position
holding the same three coördinate values as the
Vector.
See
conversionBetween.
A
Position
coördinate must be in the range
–(263)
to
263 –
2–64
inclusive.
If the
Vector
has a coördinate outside this range,
the Lua function
error
will be called.
The two callback functions are not part of the Celx Standard Library. You have to write them yourself. If you do, they will be called automatically when certain events happen. See callback.
The callbacks must be
non-local
functions.
Their error messages are written to the Celestia console
(console).
A call to
wait
inside a callback will never return.
The callbacks continue to exist after the Celx program has finished,
and can still be called by the same instance of Celestia
unless the variables that refer to them are reset to
nil
as in the example below.
Celestia:sane
does not reset these variables.
A function named
celestia_cleanup_callback
will be called when the Celx program is finished.
The simplest example is the following function that wipes itself out
to prevent the next Celx program from inheriting it.
celestia_cleanup_callback
will not be called if the Celx program calls
os.exit
or if it is terminated with the escape
key.
It will also not be called as long as there is an event handler
eventHandler).
--[[
Demonstrate a self-destructing celestia_cleanup_callback.
]]
require("std")
function celestia_cleanup_callback() --can't be local
celestia_cleanup_callback = nil
end
local function main()
--Keep the Sun in view, but get away from the glare.
local observer = celestia:sane()
observer = setposition(std.position)
end
main()
A function named
celestia_keyboard_callback
will be called when a keystroke is received.
The argument is a string containing the character that was typed.
This function is called only for characters that are letters,
digits, punctuation marks, and the blank, tab, delete (backspace) and return
characters.
To detect other characters,
call the Lua hook
keydown
in
luaHookFunctions.
A return value of
true
(or no return value at all)
indicates that the character has been completely handled
and should not also be executed as a keystroke command
(keystroke).
celestia_keyboard_callback
must be enabled with a call to
Celestia:requestkeyboard,
and will then be called while the Celx program is executing a
wait.
The keystrokes must be typed into the Celestia window,
not into the command window from which Celestia was launched.
See the example in
callback
that assembles a numeric value from a series of digits.
--[[
Display each character that is typed, followed by its code number.
If the character is multi-byte, display the number in each byte separately.
For example, the Unicode code number of the AE ligature is hexadecimal 00C6,
decimal 0198. It is encoded in UTF-8 format as the two hex bytes C3 and 86.
On Mac, pull down File -> Special Characters... -> Latin, and select AE.
On Microsoft Windows, hold down the alt key, type 0198 on the numeric keypad,
and release the alt.
]]
require("std")
function celestia_keyboard_callback(c) --can't be local
assert(type(c) == "string")
local s = string.format("\"%s\"\n", c)
for i, code in ipairs({c:byte(1, #c)}) do
s = s .. string.format("hex %02X decimal %u\n", code, code)
end
celestia:print(s, 60)
return true --Do not execute a keystroke command.
end
local function main()
--Keep the Sun in view, but get away from the glare.
local observer = celestia:sane()
observer:setposition(std.position)
celestia:requestkeyboard(true)
while true do
wait()
end
end
main()
"Æ"
hex C3 decimal 195
hex 86 decimal 134
The
gl
and
glu
tables contain
functions and the numeric constants passed to them as arguments.
The functions have no return value.
Each function calls the corresponding function in the
OpenGL
library.
For example,
gl.BlendFunc
calls
glBlendFunc
and
glu.LookAt
calls
gluLookAt.
See opengl for the sequence of function calls needed to draw graphics. This is more important than the details of the individual functions.
The
gl
(graphics library)
table is implemented in
version/src/celestia/celx_gl.cpp.
Calls to the functions
gl.Begin
and
gl.End
surround a list of
vertices
and
tex coördinates
passed to OpenGL.
The argument of
gl.Begin
must be one of the following constants.
Warning:
Celestia:getscreendimension
returns the wrong width and height between
gl.Begin
and
gl.End.
See
traceRetrograde.
See also
gl.Vertex.
If blending has been enabled with the
gl.BLEND
argument of
gl.Enable,
this function specifies how the colors of the foreground and background
will be blended together.
The only arguments provided by Celx are
gl.SRC_ALPHA
and
gl.ONE_MINUS_SRC_ALPHA.
A first argument of
gl.SRC_ALPHA
indicates that the foreground graphics and text
should have the alpha level that was assigned to them by
gl.Color.
A second argument of
gl.ONE_MINUS_SRC_ALPHA
indicates that the background should have the alpha level that is 1 minus the
alpha level that was assigned to the foreground graphics and text by
gl.Color.
For example,
if the alpha level assigned to the foreground is .25,
then the alpha levels of the foreground and background will be .25 and .75,
respectively,
for a total of 1.
Specify the red, green, blue, and alpha levels of the color.
The four arguments are in the range 0 to 1 inclusive, and default to zero.
An alpha level of 0 makes the color transparent,
1 makes it opaque.
See also
gl.BlendFunc.
Disable a capability of OpenGL.
The argument must be one of
gl.BLEND,
gl.LIGHTING,
gl.LINE_SMOOTH,
or
gl.TEXTURE_2D.
See also
gl.Enable.
Enable a capability of OpenGL.
The argument must be one of
gl.BLEND,
gl.LIGHTING,
gl.LINE_SMOOTH,
or
gl.TEXTURE_2D.
See also
gl.Disable.
Calls to the functions
gl.Begin
and
gl.End
surround a list of
vertices
and
tex coördinates
passed to OpenGL.
Warning:
Celestia:getscreendimension
returns the wrong width and height between
gl.Begin
and
gl.End.
See
traceRetrograde.
See also
gl.Vertex.
Specify the six clipping planes that define the
viewing frustum
(truncated pyramid).
Within the frustum,
closer objects appear bigger and farther objects appear smaller.
If
gl.Ortho
is called instead of
gl.Frustum,
closer and farther objects will be the same size.
Call
gl.Frustum
in the
gl.PROJECTION
matrix mode.
See also
glu.LookAt.
--[[
This file is luahook.celx.
Press the four arrow keys to demonstrate perspective and vanishing points. Draw
a "barn door": a square with crossing diagonals. The door lies in the OpenGL XY
plane because gl.Vertex can create vertices only in that plane. The OpenGL eye
is initially in front of the door, and will orbit the door when the arrow keys
are pressed.
]]
local luaHook = {
rotation = nil, --current orientation and position of OpenGL eye
axis = nil, --of rotation to apply to self.rotation for arrow key
keydown = function(self, key, modifiers)
if 1 <= key and key <= 4 then --arrow key
self.rotation = celestia:newrotation(self.axis[key],
math.rad(1)) * self.rotation
return true
end
return false
end,
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
self.rotation = std.rotation0
self.axis = {
std.yaxis, --left arrow key
-std.yaxis, --right
std.xaxis, --up
-std.xaxis --down
}
end
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
--dimensions of the Celestia window, in pixels
local width, height = celestia:getscreendimension()
local s = .125 / height
local len = 1
gl.Frustum(-s * width, s * width, -s * height, s * height,
.1, 4 * len)
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
local position = self.rotation:transform(2 * len * std.position)
local up = self.rotation:transform(std.up)
glu.LookAt(
position:getx(), position:gety(), position:getz(),
0, 0, 0, --look towards center of barn door
up:getx(), up:gety(), up:getz())
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING) --Make text and graphics self-luminous.
gl.Disable(gl.TEXTURE_2D) --disabled for graphics
gl.Color(1, 0, 0, 1) --red, green, blue, alpha
gl.LineWidth(1) --in pixels
gl.Begin(gl.LINE_LOOP) --perimeter of barn door
gl.Vertex( len, -len)
gl.Vertex( len, len)
gl.Vertex(-len, len)
gl.Vertex(-len, -len)
gl.End()
gl.Begin(gl.LINES) --two diagonals of barn door
gl.Vertex(-len, len)
gl.Vertex( len, -len)
gl.Vertex( len, len)
gl.Vertex(-len, -len)
gl.End()
gl.Begin(gl.LINE_STRIP) --uppercase L
gl.Vertex(-.2 * len, -.25 * len)
gl.Vertex(-.2 * len, -.75 * len)
gl.Vertex( .2 * len, -.75 * len)
gl.End()
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
end
}
celestia:setluahook(luaHook)
Set the line width in pixels.
The argument defaults to 1.
The line width is used when
gl.LINES,
gl.LINE_LOOP,
or
gl.LINE_STRIP
is passed to
gl.Begin.
The C++ functions
enableSmoothLines
and
disableSmoothLines
in
version/src/celengine/render.cpp
set the line width to 1.5 pixels when
gl.LINE_SMOOTH
is enabled, and to 1.0 when disabled.
Use these values to make your graphics look like Celestia’s.
Change the top matrix on the current matrix stack to the identity matrix.
This wipes out the previous value of the top matrix.
To get an expendable top matrix
that can be wiped out with no loss of information,
call
gl.PushMatrix
first.
And even before that,
call
gl.MatrixMode
to designate the current stack.
Designate the current stack of matrices.
This is important because subsequent calls to
gl.PushMatrix,
gl.PopMatrix,
etc. will be applied to the current stack.
The argument of
gl.MatrixMode
must be either
gl.PROJECTION
or
gl.MODELVIEW.
Specify the pixel coördinates of the left, right, bottom, and top
edges of the Celestia window,
and the positions of the near and far clipping planes.
Within this box,
closer and farther objects will be the same size.
If you call
gl.Frustum
instead of
gl.Ortho,
closer objects will appear bigger and farther objects will appear smaller.
Call
gl.Ortho
in the
gl.PROJECTION
matrix mode.
If you have not called
glu.LookAt,
your graphics will be two-dimensional.
In this case it would be easier to call
glu.Ortho2D
than
gl.Ortho.
Pop the top matrix off the current stack and discard it.
Call
gl.MatrixMode
first to designate the current stack.
See also
gl.PushMatrix.
Make a copy of the top matrix on the current stack and push it onto the stack.
The two top matrices are now identical.
Call
gl.MatrixMode
first to designate the current stack.
You will probably change the new top matrix
with a call to a function such as
gl.LoadIdentity.
When you’re done with the matrix,
remember to call
gl.PopMatrix.
Specify which corner of a rectangular image (a
Texture)
goes at each vertex.
The first argument is the s texture coördinate:
0 is the left edge of the image and 1 is the right edge.
The second argument is the t coördinate:
0 is the top edge and 1 is the bottom.
The arguments default to 0 and 0.
See
Texture:getwidth
and
Texture:getheight.
Adjust a number that specifies how far to translate text with
gl.Translate.
The first argument of
glu.Ortho2D
plus the amount of horizontal translation must be a number that is
1/8
greater than an integer.
Similarly,
the third argument of
glu.Ortho2D
plus the amount of vertical translation must be
1/8
greater than an integer.
gl.TexelRound
returns its first argument rounded to the closest number that would make the
sum of the arguments
1/8
greater than an integer.
If tied, it rounds up (towards positive infinity).
A missing second argument defaults to zero.
Select the magnification and minification filters for a
Texture
(image file).
The first argument is
gl.TEXTURE_2D;
the second is
gl.TEXTURE_MAG_FILTER
or
gl.TEXTURE_MIN_FILTER.
With a third argument of
gl.NEAREST,
the rendering is faster
but the individual pixels will appear as big squares
if the image file is magnified.
gl.LINEAR
is slower, but it looks better because the pixels are smoothed out.
We recommend
gl.LINEAR.
See also
gl.LINE_SMOOTH.
Translate (move) all subsequent vertices by the specified
horizontal and vertical offsets.
A positive first arguments moves the vertices to the right;
a positive second argument moves them up.
See also
glu.Ortho2D
and
gl.TexelRound.
Specify the x, y coördinates of a vertex.
A vertex may be an isolated point
(gl.POINTS),
or one of the endpoints of a line segment
(gl.LINES,
gl.LINE_STRIP,
etc).
gl.Vertex
can be called only between
gl.Begin
and
gl.End.
For gl.LINES,
there must be an even number of vertices.
For gl.QUADS,
the number of vertices must be a multiple of four.
For the
x, y coördinates,
see
glu.Ortho2D
and
gl.Translate.
To create the illusion that the vertices could have a z
coördinate too,
see
gl.Frustum
and
glu.LookAt.
For a vertex that is the corner of a
Texture,
see
gl.TexCoord.
Pass the constant
gl.BLEND
to
gl.Enable
to allow partially transparent graphics and text to be displayed on top
of the background.
Pass it to
gl.Disable
to make the graphics and text totally opaque.
See also
gl.BlendFunc.
Pass
gl.LIGHTING
to
gl.Disable
to make the graphics and text self-luminous.
Pass
gl.LINE_LOOP
to
gl.Begin
to draw a series of connected line segments
that come back to the starting point.
gl.LINE_STRIP
is the same, except that it doesn’t return to the starting point.
gl.POLYGON
is the same,
except that it fills in the polygon.
Pass
gl.LINE_SMOOTH
to
gl.Enable
to enable antialiasing when drawing lines.
Blending
must also be enabled.
Do this when the
"smoothlines"
renderflag is on to make your graphics look like Celestia’s.
See also
gl.LineWidth
and
gl.TexParameter.
Pass the argument
gl.LINE_STRIP
to
gl.Begin
to draw a series of connected line segments.
gl.LINE_LOOP
is the same,
except that it returns to the starting point.
Pass
gl.LINEAR
as the third argument of
gl.TexParameter
to specify that a linear interpolation should be used to compute the color
of each pixel in the window that is part of a
Texture
(graphics file).
The color is the weighted average of the pixels in the graphics file that
map onto or close to the pixel in the window.
gl.LINEAR
looks better than
gl.NEAREST.
Pass the argument
gl.LINES
to
gl.Begin
to draw a series of isolated line segments.
There must be an even number of calls to
gl.Vertex.
Each pair of calls specifies the endpoints for one segment.
See also
gl.LINE_STRIP
and
gl.LINE_LOOP.
Pass
gl.MODELVIEW
to
gl.MatrixMode
to make the modelview stack be the current stack of matrices.
See also
gl.PROJECTION.
Pass
gl.NEAREST
as the third argument of
gl.TexParameter
to specify that the following algorithm should be used to compute the color
of each pixel in the window that is part of a
Texture
(graphics file).
The pixel in the window is mapped onto the a point in the graphics file;
then we select the color of the pixel in the graphics file
that is closest to that point.
gl.LINEAR
looks better than
gl.NEAREST.
Pass the argument
gl.POINTS
to
gl.Begin
to draw a series of isolated points.
When passed as the second argument of
gl.BlendFunc,
this value causes the alpha level of the background to be 1 minus
the alpha level assigned to the foreground graphics and text by
gl.Color.
See also
gl.SRC_ALPHA.
Pass the argument
gl.POLYGON
to
gl.Begin
to draw a polygon filled in with a solid color.
gl.LINE_LOOP
is the same,
except it only draws the outline.
Pass
gl.PROJECTION
to
gl.MatrixMode
to make the projection stack be the current stack of matrices.
See also
gl.MODELVIEW.
Pass the argument
gl.QUADS
to
gl.Begin
to draw a series quadrilaterals.
Each quadrilateral is filled with a solid color or with a
Texture
(image file).
The number of vertices must be a multiple of four.
Pass
gl.LINE_LOOP
to draw the outline of a quadrilateral without filling it in.
When passed as the first argument of
gl.BlendFunc,
this value causes the foreground graphics and text
to have the alpha level assigned to them by
gl.Color.
See also
gl.ONE_MINUS_SRC_ALPHA.
Enable
gl.TEXTURE_2D
for text and texture files,
disable it for points and lines.
See
gl.Enable
and
gl.Disable.
gl.TEXTURE_2D
must also be the first argument of
gl.TexParameter.
Pass
gl.TEXTURE_MAG_FILTER
as the second argument to
gl.TexParameter
to specify how the pixels of a magnified
Texture
(image file) should be
mapped onto the pixels of the Celestia window.
Pass
gl.TEXTURE_MIN_FILTER
as the second argument to
gl.TexParameter
to specify how the pixels of a minified
Texture
(image file) should be
mapped onto the pixels of the Celestia window.
The
glu
table contains functions belonging to
GLU
(the OpenGL Utility Library).
The table is implemented in
version/src/celestia/celx_gl.cpp.
Specify the location and orientation of the OpenGL eye.
For example, if the eye is rolled clockwise,
the text and graphics will be rolled counterclockwise
as in the big example below.
Call this function in
matrix mode
gl.MODELVIEW.
The arguments default to zero,
but it makes no sense for all nine of them to be zero.
See also
gl.Frustum
and
Observer:lookat.
--[[
This file is luahook.celx.
Center a line of text in the Celestia window,
rotated 30 degrees counterclockwise.
]]
local luaHook = {
font = nil,
renderoverlay = function(self)
if package.loaded.std == nil then --standard lib not loaded yet
require("std")
local name = celestia:getparamstring("TitleFont")
self.font = celestia:loadfont("fonts/" .. name)
end
gl.MatrixMode(gl.PROJECTION)
gl.PushMatrix()
gl.LoadIdentity()
local width, height = celestia:getscreendimension()
glu.Ortho2D(0, width, 0, height) --left, right, bottom, top
gl.MatrixMode(gl.MODELVIEW)
gl.PushMatrix()
gl.LoadIdentity()
gl.Translate(width / 2, height / 2)
gl.Enable(gl.BLEND)
gl.BlendFunc(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA)
gl.Disable(gl.LIGHTING) --Make text self-luminous.
gl.Enable(gl.TEXTURE_2D) --Enabled for text.
gl.Color(1, 1, 1, 1) --opaque white
local theta = math.rad(30) --positive goes counterclockwise
glu.LookAt(
0, 0, 1, --location of eye
0, 0, 0, --eye is looking towards this point
math.sin(theta), math.cos(theta), 0) --up vector
local s = string.format(
"Text rotated %.15g%s counterclockwise.",
math.deg(theta), std.char.degree)
--Center the text at the origin.
local x = -self.font:getwidth(s) / 2
local y = 0
gl.Translate(gl.TexelRound(x), gl.TexelRound(y))
self.font:bind()
self.font:render(s)
gl.MatrixMode(gl.MODELVIEW)
gl.PopMatrix()
gl.MatrixMode(gl.PROJECTION)
gl.PopMatrix()
end
}
celestia:setluahook(luaHook)
Specify the pixel coördinates of the left, right, bottom, and top
edges of the Celestia window.
If you have not called
glu.LookAt,
your graphics will be two-dimensional.
In this case, it is easier to call
glu.Ortho2D
than
gl.Ortho.
Call this method in the
gl.PROJECTION
matrix mode.
If you are printing text with
Font:render,
the first and third arguments of
glu.Ortho2D
must be zero.
See
gl.TexelRound
and
gl.Translate.
A Celx program has exactly one object of class
Celestia.
It is named
celestia.
There is no way to create or destroy this object;
it already exists when the Celx program starts running
and continues to exist after the program is finished.
The
celestia
object in the Celx program is the same object as the
celestia
object in the
std.lua
file.
It is also the same object as the
celestia
in a string passed to the Lua function
loadstring
and in a file passed to
Celestia:runscript.
But the
celestia
objects in the
luahook.celx
file
(luaHookFunctions),
in a scripted orbit
(scriptedOrbit),
or in a scripted rotation
(scriptedRotation)
are not the same object as the
celestia
in the Celx program.
They don’t even share the same metatable.
A microlightyear is a millionth of a
lightyear.
KM_PER_MICROLY
is the number of
kilometers
per microlightyear.
Its value is
See the units of linear distance in
lightyear.
See also
std.c
and
std.kmPerLy.
A call to the
wait
function allows Celestia to move the simulation time forward (or backward),
to update the window,
and to call the function
celestia_keyboard_callback.
It is only during a
wait
that these things can happen;
see
wait.
The optional argument specifies the number of real-time seconds
until
wait
returns;
it defaults to zero.
wait
must be called at least once every 5 seconds of real time,
or the program will be terminated.
This limit is set by
MaxTimeslice
in
version/src/celestia/celx.cpp,
and can be changed with
Celestia:settimeslice.
A
goto
whose duration is zero seconds of real time
must be followed by a
wait
to prevent the following statements from executing at the same time as the
goto.
For other obscure occasions when
wait
must be called,
see
Celestia:settime
and the first
splitview
example in
Splitview.
wait
is implemented in
version/src/celestia/celx.cpp
as the following call to the Lua function
coroutine.yield.
function wait(seconds) --seconds of real time
coroutine.yield(seconds)
end
For this reason,
a call to
wait
will never return
if it is inside a callback function
(callback),
an event handler
(eventHandler),
a Lua hook
(luaHookFunctions),
the
position
method of a scripted orbit
(scriptedOrbit),
the
orientation
method of scripted rotation
(scriptedRotation),
or a Lua
“coroutine”.
The
std
table contains the Celx Standard Library,
named after the C++ namespace
std.
It is created when a Celx program says
require("std") --can also say require "std" without parentheses
The library also adds new methods to the Celx classes.
Although these methods are not stored in
std,
we think of them as belonging to the library anyway.
The ratio constants in
std
(“lightyears per parsec”)
are all greater than or equal to 1.
For example, the library has
std.lyPerPc
but not
std.pcPerLy.
std.auPerLy
is the number of
astronomical
units
per
lightyear.
Its value is derived as follows.
std.auPerPc
std.lyPerPc
=
63,241.0770842663
See astronomicalUnit for astronomical units and lightyear for lightyears.
local au = ly * std.auPerLy --Convert lightyears to astronomical units. local ly = ay / std.auPerLy --Convert astronomical units to lightyears.
std.auPerPc
is the number of
astronomical units
per
parsec.
Its value is
See astronomicalUnit for astronomical units and parsec for parsecs.
local au = parsecs * std.auPerPc --Convert parsecs to astronomical units. local parsecs = au / std.auPerPc --Convert astronomical units to parsecs.
std.c
is the
speed of light
in
kilometers
per
second;
the
c
stands for the Latin word
celeritas
(speed).
Its value is derived as follows.
KM_PER_MICROLY · 1,000,000
60 · 60 · 24 · 365.25
=
299,792.458
See
lightyear
for the speed of light.
See also
std.kmPerLy
and the
lightdelay
renderflag.
The string
std.celestiaVersion
gives the major version number,
minor version number,
and revision number of Celestia.
It can’t tell the difference between Celestia 1.4.0 and Celestia 1.4.1,
and reports both of them as
"1.4.0".
It can’t tell the difference between 1.5.0 and 1.5.1,
and reports both of them as
"1.5.0".
See also
std.libraryVersion
and the Lua string
_VERSION.
std.char
is a table whose keys are strings such as
"degree",
"minute",
and
"second",
and whose values are the corresponding special characters in
UTF-8 encoding
(° ′ ″).
See the standard library file
std.lua
in
stdCelx
for the list of characters.
See also
std.utf8.
Return an iterator for looping through the consecutive Celx numbers
centered at the first argument.
The second argument specifies
the number of values to visit before and after the number.
This function calls
std.next
and
std.prev.
See the example in
fullMoon.
std.constellations
is an array containing the names of the
constellations
in the file
version/src/celengine/constellation.cpp.
Each element in the array
is an array of three strings containing the name in the Latin
nominative case
("Centaurus"),
the genitive case
("Centauri", for use with the
Bayer
and
Flamsteed
designations of stars),
and a three-letter abbreviation
("Cen").
The elements are in alphabetical order by the nominative names.
The constellation
Boötes
is listed without its
diaeresis
("Bootes").
Serpens
is listed with only one name
("Serpens")
even though the file
data/asterisms.dat
has two names for it:
"Serpens Caput"
and
"Serpens Cauda".
See also
Celestia:setconstellationcolor
and
std.zodiac.
std.dayName
is an array of 7 strings containing the names of the weekdays.
It starts with Monday because the first Julian date,
January 1, 4713 B.C.,
was a Monday;
see
stepThrough.
See also
std.monthName
and the Lua function
os.date.
std.duration
is the default duration in seconds of real time for
Observer:goto
and its variants,
Observer:center,
and
Observer:centerorbit.
Its value is 5.
std.forward
is the unit vector pointing in the direction in which an
Observer
is looking.
Its value is always
(0, 0, –1).
It is measured with respect to a
Frame
whose origin is at his position,
and whose X, Y, and Z axes point to his right,
his zenith,
and his rear.
In the initial orientation of the initial
Observer
observer,
the axes of this
Frame
are parallel to those of the universal
Frame.
See also
Celestia:newrotationforwardup,
Rotation:getforwardup,
and
std.up.
Break a number into four integers: its sign bit,
the numerator and denominator
of its mantissa,
and its exponent.
See
doubleArithmetic.
The argument cannot be zero or
±math.huge,
but it can be a denormalized number
(denormalized).
The return value is a table containing the following four fields.
The
sign
field is the sign bit,
1 for negative and 0 for nonnegative.
The
numerator
is the numerator of the mantissa,
in the range
2m–1
to
2m − 1
inclusive,
where m is
std.mantissa.
The
denominator
is fixed at
2m.
The
exponent
is the power to which 2 is raised.
std.fraction
is called by
std.next
and
std.prev.
See also
std.mantissa
and the Lua function
math.frexp.
std.ftPerMile
is the number of
feet
per
statute mile.
Its value is 5280,
equal to 1760 yards.
(A
nautical mile
is something else entirely.)
See
std.mmPerIn
and
std.kmPerMile
for conversion between
English
and
metric.
The value of the
gravitational
constant
G =
6.672 · 10–11
m3
kg–1
s–2
is taken from
the data member
astro::G
in
version/src/celengine/astro.cpp.
Since a
Newton
is
1 kg m s–2,
we can also write it as
G =
6.672 · 10–11
N
m2
kg–2.
The Celestia unit of length is the microlightyear, not the meter,
so we expressed G
in
Impulse
as
std.G
(1000 ·
KM_PER_MICROLY)3
microlightyears3
kg–1
s–2
std.galacticRotation
is a
Rotation
that can be used to create a
Frame
of reference whose XZ plane is parallel to the
plane
of the
Milky Way
galaxy.
The X axis points towards the
galactic center
in
Sagittarius,
and the Y axis towards the
north galactic pole in
Coma Berenices.
This
Frame
can be used to convert between universal and galactic coördinates.
See the example in
galacticCoordinates.
See also
std.radecRotation
and
std.supergalacticRotation.
Return the horizontal field of view in radians that would be subtended
by a rectangle at a distance of 400 millimeters.
This is the distance from the user to the screen.
The arguments are the width and height of the rectangle in pixels,
defaulting to the window dimensions returned by
Celestia:getscreendimension.
The rectangle is centered in the window.
The method
Observer:gethorizontalfov
takes the
Observer’s
magnification
into account;
the function
std.gethorizontalfov
does not.
See also
std.getverticalfov
and
Observer:getmagnification.
Return the vertical field of view in radians that would be subtended
by a rectangle at a distance of 400 millimeters.
This is the distance from the user to the screen.
The arguments are the width and height of the rectangle in pixels,
defaulting to the window dimensions returned by
Celestia:getscreendimension.
The rectangle is centered in the window.
The method
Observer:getverticalfov
takes the
Observer’s
magnification
into account;
the function
std.getverticalfov
does not.
See also
std.gethorizontalfov
and
Observer:getmagnification.
std.kmPerAu
is the number of
kilometers
per
astronomical unit.
Its value of
149,597,870.7
is
taken from the macro
KM_PER_AU
in
version/src/celengine/astro.h.
See
astronomicalUnit
for astronomical units.
std.kmPerLy
is the number of
kilometers
per
light year.
Its value is derived as
KM_PER_MICROLY
=
9,460,730,472,580.8
See lightyear for lightyears.
local km = ly * std.kmPerLy --Convert lightyears to kilometers. local ly = km / std.kmPerLy --Convert kilometers to lightyears.
std.kmPerMile
is the number of
kilometers
per
mile,
derived as
std.mmPerIn
· 12
· 5,280
1,000,000
=
1.609344
local km = miles * std.kmPerMile --Convert miles to kilometers.
local miles = km / std.kmPerMile --Convert kilometers to miles.
std.kmPerPc
is the number of
kilometers
per
parsec.
It is derived as
std.kmPerAu
·
std.auPerPc
=
30,856,775,815,034.5
See parsec for parsecs.
local km = parsecs * std.kmPerPc --Convert parsecs to kilometers. local parsecs = km / std.kmPerPc --Convert kilometers to parsecs.
The string
std.libraryVersion
gives the major and minor version numbers of the Celx Standard Library.
It is currently
"1.1".
See also
std.celestiaVersion
and the Lua string
_VERSION.
std.logo
is the number of real-time seconds it takes for the CELESTIA
logo in
textures/logo.png
to fade out when Celestia is launched.
The value of 5 comes from the member function
CelestiaCore::renderOverlay
in
version/src/celestia/celestiacore.cpp.
std.lyPerPc
is the number of
lightyears
per
parsec.
It is derived as
std.kmPerPc
std.kmPerLy
=
3.26156377718021
See lightyear for lightyears, parsec for parsecs.
local ly = parsecs * std.lyPerPc --Convert parsecs to lightyears. local parsecs = ly / std.lyPerPc --Convert lightyears to parsecs.
std.mantissa
is the number of bits in the mantissa of a Celx number.
See
doubleArithmetic.
A Celx number is usually implemented as a C double
(see the macro
LUA_NUMBER
in
luaversion/src/luaconf.h),
and the number of bits in the mantissa of a C double is usually 53
(see the macro
DBL_MANT_DIG
in the C Standard Library header file
float.h).
std.mantissa
determines the value of
std.significant.
See also
std.fraction,
std.next,
and
std.prev.
std.microlyPerAu
is the number of
microlightyears
per
astronomical unit.
It is derived as
std.auPerLy
=
15.8125074098207
A microlightyear is a millionth of a lightyear. See lightyear for lightyears, astronomicalUnit for astronomical units.
--Convert microlightyears to astronomical units. local microly = au * std.microlyPerAu --Convert astronomical units to microlightyears. local au = microly / std.microlyPerAu
std.mmPerIn
is the number of
millimeters
per
inch.
Its value is exactly 25.4.
See also
std.ftPerMile.
std.monthName
is an array of strings containing the names of the 12 months in English.
To get the localized names, see
tdb.
See also
std.dayName
and the Lua function
os.date.
Return the next Celx number after the given
x,
i.e., the smallest Celx number that is bigger than
x.
The argument must not be
math.huge,
because no number comes after that.
Most of the time this function simply adds one to the argument’s
mantissa;
it calls
std.fraction
and is called by
std.consecutive.
See the example in
fullMoon.
Do not confuse
std.next
with the Lua function
next.
See also
std.prev
and
std.mantissa.
std.orientation0
is the initial orientation of the initial
Observer.
It faces him towards the
summer solstice
in
Taurus/Gemini,
with the north pole of the
ecliptic
in
Draco
overhead.
His forward vector is therefore the negative Z axis of the universal frame,
and his up vector is the Y axis.
std.orientation0
is the same object as
std.rotation0.
std.pixelsPerIn
is the number of pixels per inch.
The value of 96 comes from the initial value of the data member
CelestiaCore::screenDpi
(dots per inch)
in
version/src/celestia/celestiacore.cpp,
and the data member
Renderer::screenDpi
in
version/src/celengine/render.cpp.
std.position
is the
Position
(0, 0, 1).
From this
Position
in the universal
Frame,
the Sun is clearly visible to an
Observer
in the initial orientation
std.orientation0.
We can see where we are with respect to the Sun,
but we’re far enough away to escape its glare.
std.position0
is the
Position
(0, 0, 0).
It is the origin of a
Frame
of reference.
std.position1
is a
Position
for testing numeric conversions to and from the 128-bit format
of its coördinates
(positionCoordinates)
The values of
its coördinates are
The x coördinate has an integer of all ones and a fraction of all zeroes. The y has an integer of all zeroes and a fraction of all ones. The z has an integer of all ones and a fraction of all ones.
--Print the coordinates of std.position1 in hexadecimal --and approximate them in decimal. local hex = std.position1:gethex() local s = "" for c in std.xyz() do s = s .. string.format("%s = %s = % .15g\n", c, hex[c], std.position1[c]) end x = FFFFFFFFFFFFFFFF0000000000000000 = -1 y = 0000000000000000FFFFFFFFFFFFFFFF = 1 z = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF = -5.42101086242752e-20
Return the Celx number before the given
x,
i.e., the biggest Celx number that is smaller than
x.
The argument must not be
-math.huge,
because no number comes before that.
Most of the time, this function simply subtracts one from the argument’s
mantissa;
it calls
std.fraction
and is called by
std.consecutive.
See the example in
fullMoon.
See also
std.next
and
std.mantissa.
std.radecRotation
is a
Rotation
that can be used to create a
Frame
of reference whose XZ plane is parallel to the plane of the
celestial equator.
The X axis points towards the
vernal equinox
in
Pisces,
and the Y axis towards the
north celestial pole
near
Polaris.
This
Frame
can be used to convert between universal and equatorial coördinates.
See
rotatedRadec
and the example in
j2000Equatorial.
See also
std.galacticRotation
and
std.supergalacticRotation.
std.rotation0
is the
Rotation
of zero degrees around an irrelevant axis.
It is the same object as
std.orientation0.
Round the numeric argument to the nearest whole number.
A tie rounds upwards (towards positive infinity).
See also
gl.TexelRound
and the Lua functions
math.floor
and
math.ceil.
Return the string
"+"
if the argument is positive,
"-"
if it is negative,
and the null string if it is zero.
Useful when formatting a declination.
This plain old
"-"
(hexadecimal 0x002D)
looks okay in a monospace font,
but
std.char.minus
(hexadecimal 0x2212,
"−")
looks better in a proportional font.
std.significant
is the number of significant decimal digits that can be stored in a Celx number.
A Celx number is usually implemented as a C double
(check the macro
LUA_NUMBER
in
luaversion/src/luaconf.h),
and the number of significant decimal digits it can hold is usually 15
(check the macro
DBL_DIG
in the C Standard Library header file
float.h).
See the discussion in
doubleArithmetic.
See also
std.mantissa.
Return the value that a function should have at a time
t
in the range
t0
to
t1
inclusive.
The value at
t0
is the
v0,
the value at
t1
is
v1,
and in between it goes smoothly from
t0
to
t1.
If
v1
is greater than
v0,
the function increases slowly at the beginning,
speeds up in the middle,
and slows down again at the end.
If
v1
is less than
v0,
the function decreases slowly at the beginning,
speeds up in the middle,
and slows down again at the end.
In either case,
it’s analogous to the iPhone iOS constant
UIViewAnimationCurveEaseInOut
or the Android
AccelerateDecelerateInterpolator.
See the example in
gradualStart.
An optional fifth argument can be an interpolation function
f
defined on the closed interval
[0, 1].
It must have the following values and derivatives.
f(0) =
0
f(1) =
1
f′(0) =
0
f′(1) =
0
f
defaults to
f(t) =
–2t3
+ 3t2.
std.supergalacticRotation
is a
Rotation
that can be used to create a
Frame
of reference whose XZ plane is parallel to the
supergalactic
plane.
The X axis points towards the point in
Cassiopeia
where the galactic and supergalactic planes cross,
and the Y axis towards the
north supergalactic galactic pole in
Hercules.
This
Frame
can be used to convert between universal and supergalactic coördinates.
See the example in
supergalacticCoordinates.
See also
std.radecRotation
and
std.galacticRotation.
std.tilt
was the tilt
(obliquity)
in radians of the Earth’s axis with respect to its orbit,
at noon UTC on January 1, 2000.
The value of
23.4392911°
=
23° 26′ 21.4479599999942″
comes from the data member
astro::J2000Obliquity
in
version/src/celengine/astro.cpp.
Convert an azimuth in radians into degrees, minutes, and seconds. See altazCelobject. There are no restrictions on the argument.
The return value is a table containing fields named
degrees,
minutes,
and
seconds.
degrees is an integer in the range 0 to 359 inclusive.
minutes is an integer in the range 0 to 59 inclusive.
seconds is in the range 0 (inclusive) to 60 (exclusive).
Use
std.tolat
to convert an altitude to degrees, minutes, seconds.
See also
Position:getaltaz
and
Vector:getaltaz.
Convert a declination or altitude in radians
into degrees, minutes, seconds, and a sign.
The argument must be in the range
–π/2
to
π/2
inclusive.
It will often come from the
getlonglat
or
getaltaz
methods of classes
Position
or
Vector.
Positive is north,
negative is south,
and zero is on the equator.
The return value is a table containing fields named
degrees,
minutes,
seconds,
and
signum.
degrees is an integer in the range 0 to 90 inclusive.
minutes is an integer in the range 0 to 59 inclusive.
seconds is in the range 0 (inclusive) to 60 (exclusive).
signum
is 1 for north,
–1
for south,
and zero for neither.
It can be formatted with
std.sign.
std.tolat
does the same thing.
See also
std.tora.
and
std.toaz.
Convert a nonnegative number of days into days, hours, minutes, and seconds. The return value is a table containing fields with those four names.
days is a nonnegative integer.
hours is an integer in the range 0 to 23 inclusive.
minutes is an integer in the range 0 to 59 inclusive.
seconds is in the range 0 (inclusive) to 60 (exclusive).
Convert a latitude in radians into degrees, minutes, seconds, and a sign.
The argument must be in the range
–π/2
to
π/2
inclusive.
It will often come from
Position:getlonglat
or
Vector:getlonglat.
Positive is north,
negative is south,
and zero is on the equator.
The return value is a table containing fields named
degrees,
minutes,
seconds,
and
signum.
degrees is an integer in the range 0 to 90 inclusive.
minutes is an integer in the range 0 to 59 inclusive.
seconds is in the range 0 (inclusive) to 60 (exclusive).
signum is 1 for north,
–1
for south,
and 0 for neither.
std.todec
does the same thing.
See also
std.tolong.
Convert a longitude in radians into degrees, minutes, seconds, and a sign.
There are no restrictions on the argument.
It will often come from
Position:getlonglat
or
Vector:getlonglat.
Positive is east,
negative is west,
and zero is on the
prime meridian.
The return value is a table containing fields named
degrees,
minutes,
seconds,
and
signum.
degrees is an integer in the range 0 to 180 inclusive.
minutes is an integer in the range 0 to 59 inclusive.
seconds is in the range 0 (inclusive) to 60 (exclusive).
signum is 1 for east,
–1 for west,
and 0 for on the
prime meridian.
The argument
π is returned as
180° 0′ 0″ East.
See also
std.tolat.
Convert a right ascension in radians into hours, minutes, and seconds.
The argument must be in the range 0 (inclusive) to
2π
(exclusive).
It will often come from
Position:getlonglat
or
Vector:getlonglat.
The return value is a table containing fields named
hours,
minutes,
and
seconds.
hours is an integer in the range 0 to 23 inclusive.
minutes is an integer in the range 0 to 59 inclusive.
seconds is in the range 0 (inclusive) to 60 (exclusive).
See also
std.todec.
This function accepts one or more strings that look like numbers,
each containing an optional decimal point
and an optional leading negative sign.
It returns a list of the same number of strings,
containing the numbers encoded in the
cel:
URL format
(bits128).
The strings can be passed to
Celestia:newposition
to bypass the restrictions on precision
that would have been imposed by using Celx numbers as arguments.
See also
Celestia:geturl
and
Celestia:seturl.
std.up
is the unit vector pointing towards an
Observer’s
zenith.
Its value is always
(0, 1, 0).
It is measured with respect to a
Frame
whose origin is at his position,
and whose X, Y, and Z axes point to his right,
his zenith,
and his rear.
In the initial orientation of the initial
Observer,
the axes of this
Frame
are parallel to those of the universal
Frame.
See also
Celestia:newrotationforwardup,
Rotation:getforwardup,
and
std.forward.
This function accepts a
Unicode
code number
and returns a string consisting of the corresponding character encoded in
UTF-8.
See
specialCharacters.
The argument is a nonnegative integer in the range 0 to
231 − 1
= decimal 2,147,483,647
= hexadecimal 0x7FFFFFFF
inclusive.
The most common special characters have already been converted to UTF-8
and stored in the table
std.char.
To get the code numbers of all the characters in a font, see
inputFile.
std.xaxis
is the unit vector along the X axis.
Return an iterator that returns the three strings
"x",
"y",
"z".
These are the names of the fields of a
Position
and
Vector.
There is no corresponding function for looping through the four fields of a
Rotation.
std.yaxis
is the unit vector along the Y axis.
std.zaxis
is the unit vector along the Z axis.
The coördinate system is right-handed;
see
framesOfReference.
Find a zero (i.e., a root) of a continuous function
f
in the closed interval
[a, b].
In other words,
find a number t
such that
a ≤ t ≤ b
and
f(t) = 0.
The values
a,
b,
and
t
will usually be TDB times;
see
findZero.
If
f(a)
and
f(b)
have the same sign,
then there is no zero in
[a, b]
and
std.zero
will call the Lua function
error.
The fourth argument is a table
containing up to three terminating conditions.
std.zero
will return as soon as any of them are satisfied.
The fourth argument defaults to
{maxiter = std.mantissa}.
If the
maxiter
field is present, it is the maximum number of iterations.
It must be less than or equal to
std.mantissa.
If
delta
is present,
std.zero
will return as soon as it finds a t that is less than
delta
away from a
t0
such that
f(t0) = 0.
If
epsilon
is present,
std.zero
will return as soon as it finds a
t
at which
|f(t)| < epsilon.
std.zodiac
is an array containing the names of the 12 constellations of the zodiac,
in the traditional order starting with
"Aries".
The names are in the Latin nominative case
("Gemini",
not
"Geminorum").
For all 88 constellations,
see the array
std.constellations.
The following file
std.lua
contains the entire source code of the Celx Standard Library.
To install it,
see
standard.
A
module
is a set of objects and functions that can be made available to a Celx
program.
std.lua
creates a module named
std.
The Lua 5.1 function
package.seeall
allows the module’s functions to mention globals
and variables
such as the Lua function
type
and the Lua table
math.
Error checking would normally be performed by the Lua function
assert.
It takes two arguments, a boolean and a string.
assert(a == b,
string.format("%.15g and %.15g are unequal", a, b))
But
assert
always evaluates its second argument,
even if the first argument is
true.
This evaluation will often be an expensive call to
string.format.
The Celx Standard Library therefore performs its error checking
with the Lua function
error.
Standard library error messages contain no special characters such as
π
or
°.
Numbers in the error messages are formatted with
%.15g,
except for the large integer
%.0f
in
std.utf8.
--[[
This file is std.lua.
The Celx Standard Library for Celestia by Mark Meretzky.
This library is free software. It adds new methods to the native Celx classes
(Vector, Position, etc.) and modifies some of the existing methods. It creates
a table named std, containing variables and functions. It adds new a new
constant and a new method to the OpenGL table gl.
Contents
1. Module name and version number.
2. Constants belonging to the table std. These must be defined before the
methods and other functions, since they are used by some of the functions.
3. Class RotatedFrame.
4. Additions to the metatables of the classes implemented in Celestia,
in alphabetical order:
Celestia
Frame
Object
Observer
Position
Rotation
Vector
5. The version number of Celestia. This is derived from the metatables,
so it must come after they are accessed.
6. Additions to the OpenGL table gl.
7. Functions belonging to the table std.
]]
module("std", package.seeall) --module function deprecated in Lua 5.2.
libraryVersion = "1.1" --major and minor version numbers
--Constants:
--[[
The number of bits in the mantissa of a Celx number.
On most machines, a 64-bit C double consists of a sign bit, an 11-bit exponent,
and a 53-bit mantissa stored in 52 bits. (The first bit of the mantissa always
has the same value (1) and therefore does not need to be stored in memory.)
]]
mantissa = 1
local b = .5
while 1 + b > 1 do
mantissa = mantissa + 1
b = b / 2
end
--[[
The number of significant decimal digits that can fit in a Celx number
depends on the number of bits in the mantissa.
math.log10 is no longer present in Lua 5.2.
]]
significant = math.floor(math.log10(2^(std.mantissa - 1)))
--[[
The number of real-time seconds that the "CELESTIA" logo is displayed at
startup. See CelestiaCore::renderOverlay in version/src/celestia/celestiacore.cpp
]]
logo = 5
--[[
The default duration in real-time seconds for Observer:center,
Observer:centerorbit, and the Observer:goto methods.
]]
duration = 5
--The origin and axes of a frame of reference.
position0 = celestia:newposition(0, 0, 0)
xaxis = celestia:newvector(1, 0, 0)
yaxis = celestia:newvector(0, 1, 0)
zaxis = celestia:newvector(0, 0, 1)
--[[
std.rotation0 is the rotation whose angle is 0 radians. It does not rotate the
observer away from his initial orientation, which points towards Z == negative
infinity, with the Y axis straight up.
]]
rotation0 = celestia:newrotation(std.xaxis, 0)
orientation0 = std.rotation0
--Forward and up vectors for the observer's initial orientation,
--inherited from OpenGL.
forward = celestia:newvector(0, 0, -1)
up = celestia:newvector(0, 1, 0)
--[[
Keep the Sun reassuringly in view, but get away from its glare.
This position keeps the Sun visible if we maintain the initial orientation
std.orientation0.
]]
position = celestia:newposition(0, 0, 1)
--J2000 obliquity: tilt in degrees of Earth's axis with respect to the ecliptic
--from astro::J2000Obliquity in version/src/celengine/astro.cpp
tilt = math.rad(23.4392911)
--[[
Rotation for creating a new frame of reference whose XZ plane is parallel to the
plane of Earth's J2000 equator. X axis points towards J2000 vernal equinox in
Pisces; Y axis towards J2000 north celestial pole near Polaris.
]]
radecRotation = celestia:newrotation(std.xaxis, std.tilt)
--[[
Rotation for creating a new frame of reference whose XZ plane is parallel to the
plane of the Milky Way galaxy. X axis points towards galactic center in
Sagittarius; Y axis towards galactic north pole in Coma Berenices.
Values taken from version/src/celengine/astro.cpp.
]]
galacticRotation =
celestia:newrotation(std.yaxis, math.rad(32.932 - 90))
* celestia:newrotation(std.zaxis, math.rad(90 - 27.1283361))
* celestia:newrotation(std.yaxis, math.rad(-192.85958))
* celestia:newrotation(std.xaxis, std.tilt)
--[[
Rotation for creating a new frame of reference whose XZ plane is parallel to the
supergalactic plane. X axis points towards point in Cassiopeia where galactic
and supergalactic planes cross; Y axis towards supergalactic north pole in
Hercules. Values taken from Supergalactic coordinate system Wikipedia article.
]]
supergalacticRotation =
celestia:newrotation(std.yaxis, math.rad(-90))
* celestia:newrotation(std.zaxis, math.rad(90 - 6.32))
* celestia:newrotation(std.yaxis, math.rad(-47.37))
* std.galacticRotation
--[[
Astronomical unit in kilometers. Value taken from KM_PER_AU macro in
version/src/celengine/astro.h.
]]
kmPerAu = 149597870.7
kmPerLy = 1e6 * KM_PER_MICROLY --kilometers per lightyear
auPerPc = 1 / math.sin(2 * math.pi / (360 * 60 * 60)) --per parsec
kmPerPc = std.kmPerAu * std.auPerPc
lyPerPc = std.kmPerPc / std.kmPerLy
auPerLy = std.auPerPc / std.lyPerPc
microlyPerAu = 1e6 / std.auPerLy
--[[
mmPerIn and pixelsPerIn used in computing the default fov from the window
dimensions. Values taken from version/celestia/celestiacore.cpp.
]]
mmPerIn = 25.4
pixelsPerIn = 96
ftPerMile = 5280
kmPerMile = mmPerIn * 12 * ftPerMile / 1e6
--Speed of light in kilometers per second. "c" stands for "celerity".
c = KM_PER_MICROLY * 1e6 / (60 * 60 * 24 * 365.25)
--Gravitational constant.
--Value taken from version/src/celengine/astro.cpp.
G = 6.672e-11 --meter^3 * kilogram^-1 * second^-2
--[[
Class RotatedFrame
A RotatedFrame is a table holding a frame of reference and a rotation. The
simplest example would be a RotatedFrame that implements right ascension and
declination coordinates as seen from the Solar System Barycenter. It would be a
table holding a universal frame and a positive 23-degree rotation around the X
axis of the universal frame. The rotation would pitch the negative Z axis of
the universal frame 23 degrees down from Taurus/Gemini to Orion, thus creating a
new frame whose XZ plane is the plane of the celestial equator. The right
ascension and declination of a position or vector whose coordinates are measured
with respect to this frame could easily be read with Position:getlonglat and
Vector:getlonglat.
The transform method of the above rotation would change the vector
v = (0, 0, -1) into w = (0, -sin(23), cos(23)). Both vectors point towards
Orion. v is in the RotatedFrame described above, i.e., its coordinates are
measured with respect to the axes of the RotatedFrame. v.y is 0 because Orion
is on the plane of the celestial equator. w is in the universal frame. w.y is
negative because Orion is below the plane of the ecliptic.
Another example of a RotatedFrame: altazimuth coordinates for a given latitude
and longitude on the surface of a given body can be implemented as a
RotatedFrame holding a bodyfixed frame and a rotation. In this case, the
rotation would depend on the latitude and longitude, and would be created by
Celestia:newrotationaltaz.
]]
RotatedFrame = {
__tostring = function() return "[Frame]" end --two underscores
}
RotatedFrame.__index = RotatedFrame --two underscores
function RotatedFrame:new(frame, rotation)
if type(frame) ~= "userdata" and type(frame) ~= "table"
or tostring(frame) ~= "[Frame]" then
error("RotatedFrame:new rejects frame " .. tostring(frame))
end
if type(rotation) ~= "userdata"
or tostring(rotation) ~= "[Rotation]" then
error("RotatedFrame:new rejects rotation "
.. tostring(rotation))
end
rotatedFrame = {
frame = frame,
rotation = rotation,
conjugate = rotation^-1
}
setmetatable(rotatedFrame, self)
return rotatedFrame
end
function RotatedFrame:getrotation()
return self.rotation
end
function RotatedFrame:getcoordinatesystem()
return self.rotation:getcoordinatesystem()
end
function RotatedFrame:to(arg, t)
if type(arg) ~= "userdata" then
error("RotatedFrame:to rejects first argument "
.. tostring(arg))
end
local s = tostring(arg)
if s == "[Rotation]" then
if t == nil then
return self.frame:to(arg) * self.conjugate
end
if type(t) ~= "number" then
error("RotatedFrame:to rejects second argument "
.. tostring(t))
end
return self.frame:to(arg, t) * self.conjugate
end
if s == "[Position]" or s == "[Vector]" then
if t == nil then
return self.conjugate:transform(self.frame:to(arg))
end
if type(t) ~= "number" then
error("RotatedFrame:to rejects second argument "
.. tostring(t))
end
return self.conjugate:transform(self.frame:to(arg, t))
end
error("RotatedFrame:to rejects first argument " .. s)
end
function RotatedFrame:from(arg, t)
if type(arg) ~= "userdata" then
error("RotatedFrame:from rejects first arg " .. tostring(arg))
end
local s = tostring(arg)
if s == "[Rotation]" then
if t == nil then
return self.frame:from(arg * self.rotation)
end
if type(t) ~= "number" then
error("RotatedFrame:from rejects second argument "
.. tostring(t))
end
return self.frame:from(arg * self.rotation, t)
end
if s == "[Position]" or s == "[Vector]" then
if t == nil then
return self.frame:from(self.rotation:transform(arg))
end
if type(t) ~= "number" then
error("RotatedFrame:from rejects second argument "
.. tostring(t))
end
return self.frame:from(self.rotation:transform(arg), t)
end
error("RotatedFrame:from rejects first argument " .. s)
end
--Add new methods to the metatables of the objects implemented by Celestia.
--The classes are in alphabetical order.
--Class Celestia
local celestiaMetatable = getmetatable(celestia)
function celestiaMetatable:sane()
--We do not bother to setvisible every solar system Object.
--Do not reset the callback functions.
self:setrenderflags({automag = false})
self:setfaintestvisible(5) --default is 5 when automag is false
self:setrenderflags { --lowercase, plural
atmospheres = true,
automag = true, --show dimmer stars when zoomed in
boundaries = false, --of constellations
cloudmaps = true,
cloudshadows = true,
comettails = true,
constellations = true, --stick figures
eclipseshadows = true,
ecliptic = true,
eclipticgrid = false,
equatorialgrid = true, --same as grid
galacticgrid = false,
galaxies = true,
globulars = true, --globular clusters
grid = true, --right ascension and declination
horizontalgrid = false, --altitude and azimuth
lightdelay = false, --Turn it on for Jupiter's moons.
markers = true,
nebulae = true,
nightmaps = true, --city lights
openclusters = true,
orbits = false, --would clutter the sky
partialtrajectories = true, --nonperiodic orbits
planets = true,
ringshadows = true,
smoothlines = true, --OpenGL glEnable(GL_LINE_SMOOTH);
stars = true
}
--Although some of the orbitflags are true,
--the orbits are invisible because the orbits renderflag is false.
self:setorbitflags { --capitalized, singular
Asteroid = false,
Comet = false,
DwarfPlanet = false,
Invisible = false,
MinorMoon = false,
Moon = true,
Planet = true,
Spacecraft = false,
Star = true,
Unknown = false
}
self:setlabelflags { --lowercase, plural
asteroids = false,
comets = true,
constellations = true,
dwarfplanets = true,
galaxies = true,
globulars = true,
i18nconstellations = false, --false for Latin names
locations = false,
minormoons = false,
moons = true,
nebulae = true,
openclusters = true,
planets = true,
spacecraft = false,
stars = true
}
self:setoverlayelements { --capitalized; used in celestiacore.cpp
Frame = true, --Observer:setframe
Selection = true, --Celestia:select
Time = true, --Celestia:settime and settimescale
Velocity = true --Observer:setspeed
}
--default colors from src/celengine/render.cpp
local labelcolor = {
{"asteroids", .596, .305, .164},
{"comets", .768, .607, .227},
{"constellations", .225, .301, .36},
{"dwarfplanets", .407, .333, .964},
{"eclipticgrid", .72, .64, .88},
{"equatorialgrid", .64, .72, .88},
{"galacticgrid", .88, .72, .64},
{"galaxies", .0, .45, .5},
{"globulars", .8, .45, .5},
{"horizontalgrid", .72, .72, .72},
{"locations", .24, .89, .43},
{"moons", .231, .733, .792},
{"minormoons", .231, .733, .792},
{"nebulae", .541, .764, .278},
{"openclusters", .239, .572, .396},
{"planetographicgrid", .8, .8, .8},
{"planets", .407, .333, .964},
{"spacecraft", .93, .93, .93},
{"stars", .471, .356, .682}
}
for i, value in ipairs(labelcolor) do
self:setlabelcolor(value[1], value[2], value[3], value[4])
end
--default colors from src/celengine/render.cpp
local linecolor = {
{"asteroidorbits", .58, .152, .08},
{"boundaries", .24, .10, .12},
{"cometorbits", .639, .487, .168},
{"constellations", .0, .24, .36},
{"dwarfplanetorbits", .3, .323, .833},
{"ecliptic", .5, .1, .1},
{"eclipticgrid", .38, .28, .38},
{"equatorialgrid", .28, .28, .38},
{"galacticgrid", .38, .38, .28},
{"horizontalgrid", .38, .38, .38},
{"moonorbits", .08, .407, .392},
{"minormoonorbits", .08, .407, .392},
{"planetequator", .5, 1, 1},
{"planetographicgrid", .8, .8, .8},
{"planetorbits", .3, .323, .833},
{"selectioncursor", 1, .0, .0},
{"spacecraftorbits", .4, .4, .4},
{"starorbits", .5, .5, .8}
}
for i, value in ipairs(linecolor) do
self:setlinecolor(value[1], value[2], value[3], value[4])
end
self:setaltazimuthmode(false) --default false
self:setambient(.1) --min 0, max 1, default .1
self:setfaintestvisible(7) --default is 7 when automag is true
self:setgalaxylightgain(.5) --min 0, max 1, default .5
self:setminfeaturesize(20) --default 20 pixels
self:setminorbitsize(20) --default 20 pixels
self:setstardistancelimit(1000000) --default 1000000 lightyears
self:setstarstyle("fuzzy") --default "fuzzy"
self:settextureresolution(1) --min 0, max 2, default 1 for medium
self:settime(self:getsystemtime()) --current real time
self:settimescale(1) --default 1
self:settimeslice(5) --default 5 seconds of real time
self:setwindowbordersvisible(true) --border around every subview
self:showconstellations() --show all of them
self:unmarkall()
--Delete the event handlers.
for i, name in ipairs({"tick", "key", "mousedown", "mouseup"}) do
self:registereventhandler(name, nil)
end
--Delete every observer except the active one.
local observer = celestia:getobserver()
observer:singleview()
self:synchronizetime(true)
observer:cancelgoto()
observer:track(nil)
observer:setposition(std.position0)
observer:setorientation(std.orientation0)
observer:setverticalfov(std.getverticalfov())
--See "Planetary nomenclature" in Wikipedia.
observer:setlocationflags({
astrum = true, --star
catena = true, --chain
chaos = true, --broken or jumbled terrain
chasma = true, --hole (chasm)
city = true,
corona = true, --oval-shaped feature
crater = true,
dorsum = true, --ridge
farrum = true, --pancake-like structure, or row of them
fluctus = true, --terrain covered by volcano outflow
fossa = true, --long, narrow depression
insula = true, --island
landingsite = true,
linea = true, --line
mare = true, --sea
mensa = true, --mesa
mons = true, --mount
observatory = true,
other = true,
patera = true, --bowl
planitia = true, --low plain
planum = true, --plateau or high plain
regio = true, --region
reticulum = true, --netlike pattern on Venus
rima = true, --fissure on Moon
rupes = true, --scarp
terra = true, --land
tessera = true, --complex, ridged surface on Venus
tholus = true, --dome
undae = true, --field of dunes
vallis = true, --valley
volcano = true
})
return observer --the active observer
end
--[[
If Celestia:oldfind doesn't find what its looking for, it returns an object with
type "null" and name "?". An error thrown by the new Celestia:find can be
caught with the Lua function pcall.
]]
celestiaMetatable.oldfind = celestiaMetatable.find
function celestiaMetatable:find(name)
if type(name) ~= "string" then
error("Celestia:find rejects non-string " .. tostring(name))
end
local object = self:oldfind(name)
if type(object) ~= "userdata"
or tostring(object) ~= "[Object]"
or object:type() == "null"
or object:name() == "?" then
error("Celestia:find could not find \"" .. name .. "\"")
end
return object
end
--[[
Print "MM" at center of window, to mark the direction in which the observer is
looking. The center of the window is at the baseline between the two letters.
]]
function celestiaMetatable:mmprint(s, duration)
if s == nil then
s = ""
else
s = tostring(s)
end
if duration == nil then
duration = math.huge
elseif type(duration) ~= "number" then
error("Celestia:mmprint rejects non-numeric duration "
.. tostring(duration))
end
self:print("MM\n" .. s, duration, 0, 0, -1, 0)
end
--Add an optional trailing Rotation argument to the native Celestia:newframe.
--The three dots indicate a Lua vararg function.
celestiaMetatable.oldnewframe = celestiaMetatable.newframe
function celestiaMetatable:newframe(system, ...)
if type(system) ~= "string" then
error("Celestia:newframe rejects first argument "
.. tostring(system))
end
--At most 3 arguments after the first one.
local a = {...}
if #a > 3 then
error("Celestia:newframe accepts at most 4 arguments")
end
--i will be the subscript in a of the first argument that is not a
--celestial object.
local i = 1
local frame = nil
if system == "universal" then
frame = celestia:oldnewframe(system)
else
if type(a[i]) ~= "userdata" or tostring(a[i]) ~= "[Object]" then
error("Celestia:newframe(\"" .. system
.. "\") rejects reference object "
.. tostring(a[i]))
end
i = i + 1
if system == "ecliptic" or system == "equatorial"
or system == "bodyfixed" or system == "chase" then
frame = celestia:oldnewframe(system, a[1])
elseif system == "lock" then
if type(a[i]) ~= "userdata"
or tostring(a[i]) ~= "[Object]" then
error("Celestia:newframe(\"" .. system
.. "\") rejects target object "
.. tostring(a[i]))
end
i = i + 1
frame = celestia:oldnewframe(system, a[1], a[2])
else
error("Celestia:newframe rejects " .. system)
end
end
if i > #a then
return frame
end
if type(a[i]) ~= "userdata" or tostring(a[i]) ~= "[Rotation]" then
error("Celestia:newframe: last argument must be a rotation, "
.. "not " .. tostring(a[i]))
end
return RotatedFrame:new(frame, a[i])
end
function celestiaMetatable:newrotationforwardup(forward, up)
if type(forward) ~= "userdata" or tostring(forward) ~= "[Vector]" then
error("Celestia:newrotationforwardup rejects forward vector "
.. tostring(forward))
end
if type(up) ~= "userdata" or tostring(up) ~= "[Vector]" then
error("Celestia:newrotationforwardup rejects up vector "
.. tostring(up))
end
if (forward ^ up):length() == 0 then
error(string.format(
"Celestia:newrotationforwardup rejects colinear "
.. "(%.15g, %.15g, %.15g), (%.15g, %.15g, %.15g)",
forward:getx(), forward:gety(), forward:getz(),
up:getxyz()
))
end
return std.position0:orientationto(std.position0 + forward, up)
end
--[[
Origin at center of reference object.
X axis is parallel to a line pointing east from a given point on the surface.
Z axis is parallel to a line pointing south from the given point.
Y axis points straight up from the given point.
]]
function celestiaMetatable:newpositionaltaz(alt, az, distance)
if type(alt) ~= "number" then
error("Celestia:newpositionaltaz rejects non-numeric altitude "
.. tostring(alt))
end
if math.abs(alt) > math.pi / 2 then
error(string.format(
"Celestia:newpositionaltaz: altitude %.15g radians "
.. "must be in range -pi/2 to pi/2 inclusive", alt))
end
if type(az) ~= "number" then
error("Celestia:newpositionaltaz rejects non-numeric azimuth "
.. tostring(az))
end
if math.abs(az) >= 2 * math.pi then
error(string.format(
"Celestia:newpositionaltaz: azimuth %.15g radians "
.. "must be in range -2*pi to 2*pi exclusive", az))
end
if distance == nil then
distance = 1
else
if type(distance) ~= "number" then
error("Celestia:newpositionaltaz rejects non-numeric "
.. "distance " .. tostring(distance))
end
if distance < 0 then
error(string.format(
"Celestia:newpositionaltaz: distance %.15g "
.. "must be nonnegative", distance))
end
end
--Azimuth is measured clockwise from north (the negative Z axis),
--not counterclockwise from east (the positive X axis).
az = math.pi / 2 - az
local cosine = math.cos(alt)
return celestia:newposition(
distance * math.cos(az) * cosine,
distance * math.sin(alt),
-distance * math.sin(az) * cosine)
end
function celestiaMetatable:newpositionlonglat(long, lat, distance)
if type(long) ~= "number" then
error("newpositionlonglat rejects non-numeric longitude "
.. tostring(long))
end
if math.abs(long) >= 2 * math.pi then
error(string.format(
"Celestia:newpositionlonglat: longitude %.15g radians "
.. "must be in range -2*pi to 2*pi exclusive", long))
end
if type(lat) ~= "number" then
error("newpositionlonglat rejects non-numeric latitude "
.. tostring(lat))
end
if math.abs(lat) > math.pi / 2 then
error(string.format(
"Celestia:newpositionlonglat: latitude %.15g radians "
.. "must be in range -pi/2 to pi/2 inclusive", lat))
end
if distance == nil then
distance = 1
else
if type(distance) ~= "number" then
error("Celestia:newpositionlonglat rejects non-numeric "
.. "distance " .. tostring(distance))
end
if distance < 0 then
error(string.format(
"Celestia:newpositionlonglat: distance %.15g "
.. "must be nonnegative", distance))
end
end
local cosine = math.cos(lat)
return celestia:newposition(
distance * math.cos(long) * cosine,
distance * math.sin(lat),
-distance * math.sin(long) * cosine)
end
function celestiaMetatable:newpositionradec(ra, dec, distance)
if type(ra) ~= "number" then
error("Celestia:newpositionradec rejects non-numeric "
.. "right ascension " .. tostring(ra))
end
if math.abs(ra) >= 2 * math.pi then
error(string.format(
"Celestia:newpositionradec: right ascension %.15g "
.. "radians must be in range -2*pi to 2*pi exclusive",
ra))
end
if type(dec) ~= "number" then
error("Celestia:newpositionradec rejects non-numeric "
.. "declination " .. tostring(dec))
end
if math.abs(dec) > math.pi / 2 then
error(string.format(
"Celestia:newpositionradec: declination %.15g radians "
.. "must be in range -pi/2 to pi/2 inclusive",
dec))
end
if distance == nil then
distance = 1
else
if type(distance) ~= "number" then
error("Celestia:newpositionradec rejects non-numeric "
.. "distance " .. tostring(distance))
end
if distance < 0 then
error(string.format(
"Celestia:newpositionradec: distance %.15g "
.. "must be nonnegative", distance))
end
end
local cosine = math.cos(dec)
return celestia:newposition(
distance * math.cos(ra) * cosine,
distance * math.sin(dec),
-distance * math.sin(ra) * cosine)
end
--[[
Return the rotation passed to Celestia:newframe when creating a frame whose XZ
plane is parallel to the horizon at the point with the given latitude and
longitude.
The rotation rotates the point to the north pole in two steps. First it rotates
the point (around the Y axis) to the prime meridian, and then it rotates the
point (around the X axis) up the prime meridian to the north pole.
]]
function celestiaMetatable:newrotationaltaz(longitude, latitude)
if type(longitude) ~= "number" then
error("Celestia:newrotationaltaz rejects non-numeric longitude "
.. tostring(longitude))
end
if type(latitude) ~= "number" then
error("Celestia:newrotationaltaz rejects non-numeric latitude "
.. tostring(latitude))
end
return celestia:newrotation(std.xaxis, latitude - math.pi / 2) *
celestia:newrotation(std.yaxis, -longitude - math.pi / 2)
end
--[[
Given an altitude and azimuth, create an (x, y, z) vector that points from the
origin towards that direction. Azimuth is measured rightwards from north,
so east is at azimuth 90 degrees.
The XZ plane is the plane of the horizon. X axis points east, Z axis points
south, Y axis points up.
]]
function celestiaMetatable:newvectoraltaz(alt, az, distance)
if type(alt) ~= "number" then
error("Celestia:newvectoraltaz rejects non-numeric altitude "
.. tostring(alt))
end
if math.abs(alt) > math.pi / 2 then
error(string.format(
"Celestia:newvectoraltaz: altitude %.15g radians "
.. "must be in range -pi/2 to pi/2 inclusive", alt))
end
if type(az) ~= "number" then
error("Celestia:newvectoraltaz rejects non-numeric azimuth "
.. tostring(az))
end
if math.abs(az) >= 2 * math.pi then
error(string.format(
"Celestia:newvectoraltaz: azimuth %.15g radians "
.. "must be in range -2*pi to 2*pi exclusive", az))
end
if distance == nil then
distance = 1
else
if type(distance) ~= "number" then
error("Celestia:newvectoraltaz rejects non-numeric "
.. "distance " .. tostring(distance))
end
if distance < 0 then
error(string.format(
"Celestia:newvectoraltaz: distance %.15g "
.. "must be nonnegative", distance))
end
end
--Azimuth is measured clockwise from north (the negative Z axis),
--not counterclockwise from east (the positive X axis).
az = math.pi / 2 - az
local cosine = math.cos(alt)
return celestia:newvector(
distance * math.cos(az) * cosine,
distance * math.sin(alt),
-distance * math.sin(az) * cosine)
end
function celestiaMetatable:newvectorlonglat(long, lat, distance)
if type(long) ~= "number" then
error("Celestia:newvectorlonglat rejects non-numeric longitude "
.. tostring(long))
end
if math.abs(long) >= 2 * math.pi then
error(string.format(
"Celestia:newvectorlonglat: longitude %.15g radians "
.. "must be in range -2*pi to 2*pi exclusive", long))
end
if type(lat) ~= "number" then
error("Celestia:newvectorlonglat rejects non-numeric latitude "
.. tostring(lat))
end
if math.abs(lat) > math.pi / 2 then
error(string.format(
"Celestia:newvectorlonglat: latitude %.15g radians "
.. "must be in range -pi/2 to pi/2 inclusive", lat))
end
if distance == nil then
distance = 1
else
if type(distance) ~= "number" then
error("Celestia:newvectorlonglat rejects non-numeric "
.. "distance " .. tostring(distance))
end
if distance < 0 then
error(string.format(
"Celestia:newvectorlonglat: distance %.15g "
.. "must be nonnegative", distance))
end
end
local cosine = math.cos(lat)
return celestia:newvector(
distance * math.cos(long) * cosine,
distance * math.sin(lat),
-distance * math.sin(long) * cosine)
end
--Return a vector in universal coordinates pointing to the given right ascension
--and declination.
function celestiaMetatable:newvectorradec(ra, dec, distance)
if type(ra) ~= "number" then
error("Celestia:newvectorradec reject non-numeric "
.. "right ascension " .. tostring(ra))
end
if math.abs(ra) >= 2 * math.pi then
error(string.format("Celestia:newvectorradec: right ascension "
.. "%.15g radians must be in range -2*pi to 2*pi "
.. "exclusive", ra))
end
if type(dec) ~= "number" then
error("Celestia:newvectorradec rejects non-numeric declination "
.. tostring(dec))
end
if math.abs(dec) > math.pi / 2 then
error(string.format(
"Celestia:newvectorradec: declination %.15g "
.. "radians must be in range -pi/2 to pi/2 inclusive",
dec))
end
if distance == nil then
distance = 1
else
if type(distance) ~= "number" then
error("Celestia:newvectorradec reject non-numeric "
.. "distance " .. tostring(distance))
end
if distance < 0 then
error(string.format(
"Celestia:newvectorradec: distance %.15g "
.. "must be nonnegative", distance))
end
end
local cosine = math.cos(dec)
return std.radecRotation:transform(celestia:newvector(
distance * math.cos(ra) * cosine,
distance * math.sin(dec),
-distance * math.sin(ra) * cosine))
end
--Class Frame
--The Celx methods Frame:from and Frame:to accept a Position or a Rotation.
--Make them accept a Vector too.
local frameMetatable = getmetatable(celestia:newframe("universal"))
frameMetatable.oldfrom = frameMetatable.from
frameMetatable.oldto = frameMetatable.to
function frameMetatable:from(arg, t)
if type(arg) ~= "userdata" then
error("Frame:from rejects non-userdata " .. tostring(arg))
end
local s = tostring(arg)
if s == "[Position]" or s == "[Rotation]" then
if t == nil then
return self:oldfrom(arg)
end
if type(t) == "number" then
return self:oldfrom(arg, t)
end
error("Frame:from rejects non-numeric time " .. tostring(t))
end
if s ~= "[Vector]" then
error("Frame:from rejects first argument " .. tostring(s))
end
if t == nil then
return self:oldfrom(arg:toposition())
- self:oldfrom(std.position0)
end
if type(t) == "number" then
return self:oldfrom(arg:toposition(), t)
- self:oldfrom(std.position0, t)
end
error("Frame:from rejects non-numeric time " .. tostring(t))
end
function frameMetatable:to(arg, t)
if type(arg) ~= "userdata" then
error("Frame:to rejects non-userdata " .. tostring(arg))
end
local s = tostring(arg)
if s == "[Position]" or s == "[Rotation]" then
if t == nil then
return self:oldto(arg)
end
if type(t) == "number" then
return self:oldto(arg, t)
end
error("Frame:to rejects non-numeric time " .. tostring(t))
end
if s ~= "[Vector]" then
error("Frame:to rejects first argument " .. s)
end
if t == nil then
return self:oldto(arg:toposition()) - self:oldto(std.position0)
end
if type(t) == "number" then
return self:oldto(arg:toposition(), t)
- self:oldto(std.position0, t)
end
error("Frame:to rejects non-numeric time " .. tostring(t))
end
--Class Object
--[[
There may be no selected object at this point. But the dummy object returned
by getselection suffices to get us the metatatble.
]]
local objectMetatable = getmetatable(celestia:getselection())
--[[
Return the pathname of the object, e.g.
"Solar System Barycenter/Sol/Earth/Moon". Two objects are the same object if
their pathnames are equal.
]]
function objectMetatable:pathname()
local object = self
local name = object:name()
while true do
object = object:getinfo().parent
if object == nil then
return name
end
name = object:name() .. "/" .. name
end
end
--[[
An iterator for looping through an object, its children, grandchildren, etc.,
in preorder. The root object is at level 0; its children are at level 1, etc.
local s = ""
for level, object in celestia:find("Sol"):family() do
s = s .. level .. " " .. object:name() .. "\n"
end
]]
function objectMetatable:family()
--[[
Create and return an anonymous function and a stack. The stack is a
stack of arrays, initially consisting of just one array. Each array
holds a level number and a celestial Object.
The anonymous function is an iterator. It receives a stack as an
argument, and returns the next celestial Object (and the level thereof)
to be visited in a preorder traversal. The root of the tree is at level
zero.
]]
return function(stack)
if type(stack) ~= "table" then
error("Object:family iterator requires table, not "
.. tostring(stack))
end
local t = table.remove(stack)
if t == nil then
return
end
if type(t) ~= "table" then
error("Object:family iterator requires table on top of "
.. "stack, not " .. tostring(t))
end
local level = t[1]
if type(level) ~= "number" then
error("Object:family iterator demands number as first "
.. "array element, not " .. tostring(level))
end
local obj = t[2]
if type(obj) ~= "userdata" or tostring(obj) ~= "[Object]" then
error("Object:family iterator demands celestial object "
.. "as second array element, not "
.. tostring(obj))
end
if #t ~= 2 then
error("Object:family iterator requires two-element "
.. "array on top of stack")
end
local children = obj:getchildren()
for i = #children, 1, -1 do
table.insert(stack, {level + 1, children[i]})
end
return level, obj
end, {{0, self}} --The root of the tree is at level 0.
end
--Class Observer
local observerMetatable = getmetatable(celestia:getobserver())
observerMetatable.oldsetframe = observerMetatable.setframe
function observerMetatable:setframe(arg)
if tostring(arg) ~= "[Frame]" then
error("Observer:setframe rejects non-Frame " .. tostring(arg))
end
local t = type(arg)
if t == "userdata" then
self:oldsetframe(arg)
elseif t == "table" then
self:oldsetframe(arg.frame)
else
error("Observer:setframe demands userdata or table, not " .. t
.. " " .. tostring(arg))
end
end
--[[
Get and set the horizontal and vertical fields of view, in radians,
either of the whole window or of the width by height rectangle thereof.
Observer:getfov and Observer:setfov get and set the vertical field of view.
]]
observerMetatable.setverticalfov = observerMetatable.setfov
function observerMetatable:gethorizontalfov(width, height)
if width == nil and height == nil then
width, height = celestia:getscreendimension()
elseif type(width) ~= "number" or type(height) ~= "number" then
error("Observer:gethorizontalfov rejects non-numeric "
.. tostring(width) .. ", " .. tostring(height))
end
local w, h = celestia:getscreendimension()
--user's distance in pixels from the center of the Celestia window.
local d = h / (2 * math.tan(self:getfov() / 2))
return 2 * math.atan2(width / 2, d)
end
function observerMetatable:getverticalfov(width, height)
if width == nil and height == nil then
width, height = celestia:getscreendimension()
elseif type(width) ~= "number" or type(height) ~= "number" then
error("Observer:getverticalfov rejects non-numeric "
.. tostring(width) .. ", " .. tostring(height))
end
local w, h = celestia:getscreendimension()
--user's distance in pixels from the center of the Celestia window.
local d = h / (2 * math.tan(self:getfov() / 2))
return 2 * math.atan2(height / 2, d)
end
function observerMetatable:sethorizontalfov(hfov)
if type(hfov) ~= "number" or hfov <= 0 then
error("Observer:sethorizontalfov demands positive number, not "
.. tostring(hfov))
end
local w, h = celestia:getscreendimension()
--user's distance in pixels from the center of the Celestia window.
local d = h / (2 * math.tan(hfov / 2))
self:setfov(2 * math.atan2(w / 2, d))
end
function observerMetatable:getmagnification()
local width, height = celestia:getscreendimension()
return std.getverticalfov(width, height) / self:getfov()
end
function observerMetatable:setmagnification(magnification)
if type(magnification) ~= "number" or magnification <= 0 then
error("Observer:setmagnification demands positive numeric "
.. "magnification, not " .. tostring(self))
end
local width, height = celestia:getscreendimension()
self:setverticalfov(std.getverticalfov(width, height) / magnification)
end
--[[
Return the pixel coordinates where the position appears in the Celestia window.
The position object is in the universal frame. The pixel (0, 0) is at the
center of the Celestia window. x increases to the right, y increases up.
]]
function observerMetatable:getscreencoordinates(position)
if type(position) ~= "userdata"
or tostring(position) ~= "[Position]" then
error("Observer:getscreencoordinates rejects non-position "
.. tostring(position))
end
--vector from the observer to the position
local v = position - self:getposition()
--This statement needed only when observer not in initial orientation.
v = self:getorientation():conjugate():transform(v)
if v.z >= 0 then
--Position is invisible because it's behind the observer.
return nil, nil
end
--User's distance in pixels from the screen.
--Observer:getfov returns the vertical field of view.
local width, height = celestia:getscreendimension()
local distance = height / (2 * math.tan(self:getfov() / 2))
local factor = -distance / v.z
local x = factor * v.x
if math.abs(x) > width / 2 then
--Position is too far left or right to be in the window.
return nil, nil
end
local y = factor * v.y
if math.abs(y) > height / 2 then
--Position is too high or too low to be in the window.
return nil, nil
end
return x, y
end
--[[
The standard library Observer:splitview is the same as the Celx one,
except that it returns the new observer.
]]
observerMetatable.oldsplitview = observerMetatable.splitview
function observerMetatable:splitview(direction, fraction)
if type(direction) ~= "string" then
error("Observer:splitview rejects non-string first argument "
.. tostring(direction))
end
if fraction == nil then
self:oldsplitview(direction)
elseif type(fraction) == "number" then
self:oldsplitview(direction, fraction)
else
error("Observer:splitview rejects non-nil, non-numeric second "
.. "argument " .. tostring(direction))
end
local t = celestia:getobservers()
return t[#t] --The observer oldsplitview just created is the last one.
end
--Class Position
local positionMetatable = getmetatable(celestia:newposition(0, 0, 0))
--[[
Make it easy to format the coordinates of a position:
local s = string.format("(%.15g, %.15g, %.15g)", position:getxyz())
The getxyz must be the last argument of the string.format.
]]
function positionMetatable:getxyz()
return self:getx(), self:gety(), self:getz()
end
--[[
In Mathematics, the axis perpendicular to the X axis in the fundamental plane is
the Y axis, and it points up. In Celestia, the axis perpendicular to the X axis
in the fundamental plane is the Z axis, and it points down. That's why the z
has a negative sign.
]]
function positionMetatable:getlonglat()
local x = self:getx()
local y = self:gety()
local z = self:getz()
local longitude = 0 --east is positive
if x ~= 0 or z ~= 0 then
longitude = math.atan2(-z, x)
if longitude < 0 then
longitude = longitude + 2 * math.pi
--If the original longitude was a tiny negative
--fraction, the above addition might result in
--2 * math.pi.
if longitude == 2 * math.pi then
longitude = 0
end
end
end
local latitude = 0 --north is positive
local d = math.sqrt(x*x + z*z)
if y ~= 0 or d ~= 0 then
latitude = math.atan2(y, d)
end
return {
latitude = latitude,
longitude = longitude,
distance = math.sqrt(x*x + y*y + z*z)
}
end
--[[
Longitude and azimuth are both measured in the XZ plane.
Longitude is counterclockwise from the positive X axis,
but azimuth is clockwise from the negative Z axis.
]]
function positionMetatable:getaltaz()
local longlat = self:getlonglat()
local azimuth = 0
if self:getx() ~= 0 or self:getz() ~= 0 then
azimuth = math.pi / 2 - longlat.longitude
if azimuth < 0 then
azimuth = azimuth + 2 * math.pi
--If the original azimuth was a tiny negative fraction,
--the above addition might result in 2 * math.pi.
if azimuth == 2 * math.pi then
azimuth = 0
end
end
end
return {
altitude = longlat.latitude,
azimuth = azimuth,
distance = longlat.distance
}
end
--Position can be multiplied by a number on the left or right: n * position or
--position * n.
positionMetatable.__mul = function(left, right)
local position = nil
local n = nil
if type(left) == "userdata" and tostring(left) == "[Position]" then
if type(right) ~= "number" then
error("Position can be multiplied only by a number, "
.. "not by " .. tostring(right))
end
position = left
n = right
elseif type(right) == "userdata" and tostring(right) == "[Position]"
then
if type(left) ~= "number" then
error("Position can be multiplied only by a number, "
.. "not by " .. tostring(left))
end
position = right
n = left
else
error("bad position multiplication: " .. tostring(left) .. " "
.. tostring(right))
end
return celestia:newposition(
n * position:getx(),
n * position:gety(),
n * position:getz())
end
--Unary minus.
function positionMetatable:__unm()
return -1 * self
end
function positionMetatable:__div(divisor)
if type(divisor) ~= "number" then
error("Position can't be divided by non-numeric "
.. tostring(n))
end
if divisor == 0 then
error(string.format("position (%.15g, %.15g, %.15g) "
.. "can't be divided by zero", self:getxyz()))
end
return self * (1 / divisor)
end
--Convert the Position to a Vector.
function positionMetatable:tovector()
return celestia:newvector(self:getxyz())
end
--[[
Strings passed to Celestia:newposition contain the following characters.
The characters also appear in the encoding of a position in a Celx URL.
]]
local urlChars =
"ABCDEFGHIJKLMNOPQRSTUVWXYZ"
.. "abcdefghijklmnopqrstuvwxyz"
.. "0123456789"
.. "+/"
--Convert one octal digit to the corresponding trio of binary digits.
--Used only by the following function.
local octalToBinary = {
["0"] = "000",
["1"] = "001",
["2"] = "010",
["3"] = "011",
["4"] = "100",
["5"] = "101",
["6"] = "110",
["7"] = "111"
}
--[[
Convert "A" to "000000". First convert the "A" to two octal digits ("00").
Then convert each octal digit to three bits.
]]
local function charToSextet(char)
local n = urlChars:find(char)
local s = string.format("%02o", n - 1)
return s:gsub(".", octalToBinary)
end
--[[
Change the Celx URL encoding of a Position coordinate into a string of 128 "1"s
and "0"s.
]]
local function urltobin(url)
if type(url) ~= "string" then
error("std.urltobin requires string, not " .. tostring(url))
end
local startIndex, endIndex = url:find("[^%w+/ ]")
if startIndex ~= nil then
error("std.urltobin: string \"" .. url .. "\"cannot contain \""
.. url:sub(startIndex, endIndex) .. "\"")
end
local bin = url:gsub(" ", ""):gsub(".", charToSextet)
if bin:len() < 128 then
bin = bin .. ("0"):rep(128 - bin:len())
elseif bin:len() == 132 and bin:sub(-4) == "0000" then
bin = bin:sub(1, -5) --remove trailing "0000"
else
error("std.urltobin: bad string \"" .. bin .. "\" of length "
.. bin:len())
end
return bin:reverse():gsub("........", string.reverse)
end
--[[
Change a string of 128 "1"s and "0"s into the Celx URL encoding of a position
coordinate. The resulting string can be passed as an argument to
Celestia:newposition.
Most significant byte of binary is on the left.
Most significant bit of each byte is on the left.
]]
local function bintourl(binary)
if type(binary) ~= "string" then
error("std.bintourl demands string, not " .. tostring(binary))
end
if binary:len() ~= 2^7 then
error("std.bitourl demands string of length " .. 2^7
.. ", not " .. binary:len())
end
--Put the most significant bit of each byte on the right.
binary = binary:gsub("........", string.reverse)
--Put the most significant byte on the right.
--The most significant bit of each byte is now on the left again.
binary = binary:reverse()
binary = binary .. "0000" --Make length a multiple of 6.
local charCount = 0
local lastNon0 = 0
binary = binary:gsub("......", function(sextet)
charCount = charCount + 1
if sextet ~= "000000" then
lastNon0 = charCount
end
local n = tonumber(sextet, 2) + 1
return urlChars:sub(n, n)
end)
if 6 * lastNon0 % 8 > 0 then
--Remove all but one of the trailing "A"s.
--The "A" that we keep completes the last nonzero byte.
return binary:gsub("A+$", "A")
end
--Remove all of the trailing "A"s.
return binary:gsub("A*$", "")
end
--[[
An iterator for looping through the names of the three fields of a Position or
Vector.
local s = ""
for c in std.xyz() do
s = s .. string.format("v.%s == %.15g\n", c, v[c])
end
]]
function xyz()
local t = {"x", "y", "z"}
local i = 0 --the first key minus 1
return function()
i = i + 1
if i <= #t then
return t[i]
end
end
end
--[[
digitString is a string of digits in base base. Add n to the number spelled out
in this string and return the sum in the same base. For example,
add(2, "10", 2) returns "100".
add(10, "10", 2) returns "12".
]]
local function add(base, digitString, n)
if type(base) ~= "number" or base ~= 2 and base ~= 10 then
error("std.add: base must be 2 or 10, not " .. tostring(base))
end
if type(digitString) ~= "string" then
error("std.add rejects digitString " .. tostring(digitString))
end
if type(n) ~= "number" or n < 0 then
error("std.add demands nonnegative number, not "
.. tostring(n))
end
local sum = ""
for digit in digitString:reverse():gmatch(".") do --right to left
local s = digit + n
sum = s % base .. sum
n = math.floor(s / base)
end
while n > 0 do
sum = n % base .. sum
n = math.floor(n / base)
end
return sum
end
--[[
digitString is a string of digits in base base. Multiply the number spelled out
in this string by n and return the product in the same base. For example,
mult( 2, "11", 2) returns "110".
mult(10, "40", 3) returns "120".
]]
local function mult(base, digitString, n)
if type(digitString) ~= "string" then
error("std.mult rejects digitString " .. tostring(digitString))
end
if type(n) ~= "number" or n < 0 then
error("std.mult demands nonnegative numeric factor, not "
.. tostring(n))
end
local pattern = nil
if base == 2 then
pattern = "[01]"
elseif base == 10 then
pattern = "%d"
else
error("mult rejects base " .. tostring(base))
end
local carry = 0
local product = ""
for digit in digitString:reverse():gmatch(pattern) do
local p = digit * n + carry
product = p % base .. product
carry = math.floor(p / base)
end
while carry > 0 do
product = carry % base .. product
carry = math.floor(carry / base)
end
return product
end
--Divide the binary digitString by n. Discard any remainder.
--For example, div("101", 2) returns "010" (same number of characters).
local function div2(digitString, n)
if type(digitString) ~= "string" then
error("std.div2 rejects digitString " .. tostring(digitString))
end
if type(n) ~= "number" or n <= 0 then
error("std.div2 demands positive numeric divisor, not "
.. tostring(n))
end
local dividend = 0
local quotient = ""
for bit in digitString:gmatch("[01]") do
dividend = 2 * dividend + bit
quotient = quotient .. math.floor(dividend / n)
dividend = dividend % n
end
return quotient
end
--Divide the decimal string by n. For example, div("1", 2) returns ".5".
local function div10(digitString, n)
if type(digitString) ~= "string" then
error("std.div10 rejects digitString " .. tostring(digitString))
end
if type(n) ~= "number" or n <= 0 then
error("std.div10 demands positive numeric divisor, not "
.. tostring(n))
end
local dividend = 0
local quotient = ""
--Count the digits to the left of the decimal point.
--Then remove the decimal point.
local d = (digitString .. "."):find("%.") - 1
digitString:gsub("%.", "")
for digit in digitString:gmatch("%d") do
dividend = 10 * dividend + digit
quotient = quotient .. math.floor(dividend / n)
dividend = dividend % n
end
while dividend > 0 do
dividend = 10 * dividend
local q = math.floor(dividend / 2)
quotient = quotient .. q
dividend = dividend % n
end
if quotient:len() > d then
quotient = quotient:sub(1, d) .. "." .. quotient:sub(d + 1)
end
return quotient:gsub("^0*(%d)", "%1")
end
--[[
Return a table of three strings, each containing 128 "1"s and "0"s.
Each string begins with the most significant bit of the most significant byte.
]]
function positionMetatable:getbinary()
local bit = {
[false] = "0",
[true] = "1"
}
local binary = {}
for c in std.xyz() do
binary[c] = ""
end
--Examine the bits, one by one, from left to right.
for i = 1, 2^7 do
for c in std.xyz() do
--Test the sign bit.
--The sign bit is 1 if the number is negative.
binary[c] = binary[c] .. bit[self[c] < 0]
end
--Shift each bit in each coordinate one place to the left.
self = self + self
end
return binary
end
--Return a table of three strings, each containing 32 hex digits.
function positionMetatable:gethex()
local binary = self:getbinary()
local hex = {}
for c in std.xyz() do
hex[c] = binary[c]:gsub("....", function(nibble)
return string.format("%X", tonumber(nibble, 2))
end)
end
return hex
end
--Return three strings that can be passed to Celestia:newposition.
function positionMetatable:geturl()
--Leftmost byte is most significant.
--Leftmost bit in each byte is most significant.
local binary = self:getbinary()
local url = {}
for c in std.xyz() do
url[c] = bintourl(binary[c])
end
return url
end
--Return a table of three strings, each containing a decimal number.
function positionMetatable:getdecimal()
local binary = self:getbinary()
local flip = {
["0"] = "1",
["1"] = "0"
}
local negative = {}
for c in std.xyz() do
negative[c] = binary[c]:find("^1")
if negative[c] then
--Two's complement negation: flip the bits and add 1.
binary[c] = binary[c]:gsub("[01]", flip)
binary[c] = add(2, binary[c], 1):sub(-128)
end
end
local decimal = {}
for c in std.xyz() do
decimal[c] = ""
end
for c in std.xyz() do
for bit in binary[c]:gmatch("[01]") do
decimal[c] = mult(10, decimal[c], 2)
decimal[c] = add(10, decimal[c], tonumber(bit))
end
end
for i = 0, 64 - 1 do
for c in std.xyz() do
decimal[c] = div10(decimal[c], 2)
end
end
for c in std.xyz() do
if decimal[c] == "" then
decimal[c] = "0"
elseif negative[c] then
decimal[c] = "-" .. decimal[c]
end
end
return decimal
end
--[[
Accepts 1, 2, or 3 arguments. Each argument must be a string consisting of two
strings of decimal digits (at least one of which must be non-empty), separated
by an optional decimal point, and preceded by an optional negative sign.
Return the same number of strings, converted to URL format.
The three dots indicate a Lua vararg function.
]]
function tourl(...)
local a = {...}
if #a <= 0 then
error("std.tourl requires 1, 2, or 3 arguments")
end
local coordinate = {}
for i, c in ipairs(a) do
if type(c) ~= "string" then
error("std.tourl rejects non-string " .. tostring(c))
end
if not c:find("^-?%d*%.?%d*$") or not c:find("%d") then
error("std.tourl rejects malformed \"" .. c .. "\"")
end
table.insert(coordinate, c)
end
local binary = {}
local seenDecimal = {}
local decimalPlaces = {}
local negative = {}
for i, c in ipairs(coordinate) do
--Record and remove the optional leading negative sign.
c, nmatches = c:gsub("^-", "")
table.insert(negative, nmatches == 1)
--[[
Convert the decimal argument to a binary string.
decimalPlaces counts the places to the right of the decimal
point.
For example, "12" becomes "1100" with decimalPlaces == 0.
"1.2" also becomes "1100", but with decimalPlaces == 1.
And ".12" becomes "1100", with decimalPlaces == 2.
]]
table.insert(binary, "0")
table.insert(seenDecimal, false)
--number of digits to right of decimal point
table.insert(decimalPlaces, 0)
for char in c:gmatch(".") do
if char == "." then
seenDecimal[i] = true
else
binary[i] = mult(2, binary[i], 10)
binary[i] = add(2, binary[i], tonumber(char))
if seenDecimal[i] then
decimalPlaces[i] = decimalPlaces[i] + 1
end
end
end
--Multiply binary[i] by 2^64
binary[i] = binary[i] .. string.rep("0", 64)
--Divide binary[i] by 10^decimalPlaces[i].
--We do this by dividing binary[i] by 10 decimalPlaces[i] times.
for j = 1, decimalPlaces[i] do
binary[i] = div2(binary[i], 10)
end
--Remove leading zeroes.
binary[i] = binary[i]:gsub("^0*", "")
if binary[i]:len() >= 128 and
(not negative[i]
or binary[i] ~= "1" .. string.rep("0", 128 - 1)) then
error("std.tourl: argument must be of the form "
.. "n * 2^-64,\n"
.. "where n is an integer in the range "
.. "-2^127 to 2^127-1 inclusive")
end
if negative[i] then
--Make sure binary[i] is at least 128 bits long so that
--the two's complement will sign-extend far enough.
binary[i] = string.rep("0", 128) .. binary[i]
--Two's complement negation: flip the bits and add 1.
binary[i] = binary[i]:gsub("[01]",
{["0"] = "1", ["1"] = "0"})
binary[i] = add(2, binary[i], 1)
end
--Make sure binary[i] is no longer than 128 characters.
--Discard all but the rightmost 128 characters of binary[i].
binary[i] = binary[i]:sub(-128)
if binary[i]:len() < 128 then
binary[i] =
("0"):rep(128 - binary[i]:len()) .. binary[i]
end
binary[i] = bintourl(binary[i])
end
--Lua 5.1 does not have table.unpack.
if #a == 1 then
return binary[1]
end
if #a == 2 then
return binary[1], binary[2]
end
if #a == 3 then
return binary[1], binary[2], binary[3]
end
end
--[[
A Position for testing purposes: (-1, 1 - 2^-64, -(2^-64))
= (-1,
.9999999999999999999457898913757247782996273599565029144287109375,
-.0000000000000000000542101086242752217003726400434970855712890625)
x has an integer of all ones and a fraction of all zeroes.
y has an integer of all zeroes and a fraction of all ones.
z has an integer of all ones and a fraction of all ones.
]]
position1 = celestia:newposition(
(bintourl(("1"):rep(2^6) .. ("0"):rep(2^6))), --Lua needs extra parens
(bintourl(("0"):rep(2^6) .. ("1"):rep(2^6))),
(bintourl(("1"):rep(2^6) .. ("1"):rep(2^6)))
)
--Class Rotation
local rotationMetatable =
getmetatable(celestia:newrotation(celestia:newvector(1, 0, 0), 0))
--The Celx method Rotation:transform accepts a vector.
--Make it accept a position too.
rotationMetatable.oldtransform = rotationMetatable.transform
function rotationMetatable:transform(arg)
if type(arg) ~= "userdata" then
error("Rotation:transform rejects " .. tostring(arg))
end
if tostring(arg) == "[Vector]" then
return self:oldtransform(arg)
end
if tostring(arg) == "[Position]" then
return self:oldtransform(arg:tovector()):toposition()
end
error("Rotation:transform rejects " .. tostring(arg))
end
--[[
Return the same rotation, but in the opposite direction.
We have to negate the axis, not the angle, because the angle is always in the
range 0 to 2pi radians inclusive.
]]
function rotationMetatable:conjugate()
return celestia:newrotation(self.w, -self.x, -self.y, -self.z)
end
function rotationMetatable:__pow(n)
if type(n) ~= "number" or n ~= -1 then
error("Rotation:__pow right operand must be the number -1, "
.. "not " .. tostring(n))
end
return self:conjugate()
end
function rotationMetatable:getforwardup()
return self:transform(std.forward), self:transform(std.up)
end
--Class Vector
local vectorMetatable = getmetatable(celestia:newvector(0, 0, 0))
--[[
Make it easy to print the coordinates of a vector:
local s = string.format("(%.15g, %.15g, %.15g)", vector:getxyz())
The getxyz must be the last argument of the string.format.
]]
function vectorMetatable:getxyz()
return self:getx(), self:gety(), self:getz()
end
function vectorMetatable:getlonglat()
local x = self:getx()
local y = self:gety()
local z = self:getz()
local longitude = 0 --east is positive
if x ~= 0 or z ~= 0 then
longitude = math.atan2(-z, x)
if longitude < 0 then
longitude = longitude + 2 * math.pi
--If the original longitude was a tiny negative
--fraction, the above addition might result in
--2 * math.pi.
if longitude == 2 * math.pi then
longitude = 0
end
end
end
local latitude = 0 --north is positive
local d = math.sqrt(x*x + z*z)
if y ~= 0 or d ~= 0 then
latitude = math.atan2(y, d)
end
return {
latitude = latitude,
longitude = longitude,
distance = self:length()
}
end
function vectorMetatable:getaltaz()
local longlat = self:getlonglat()
local azimuth = math.pi / 2 - longlat.longitude
if azimuth < 0 then
azimuth = azimuth + 2 * math.pi
--If the original azimuth was a tiny negative fraction,
--the above addition might result in 2 * math.pi.
if azimuth == 2 * math.pi then
azimuth = 0
end
end
return {
altitude = longlat.latitude,
azimuth = azimuth,
distance = longlat.distance
}
end
--[[
Convert the Vector to a Position.
-2^63 is the only value that can be stored in a Celx number (64-bit floating
point) and in a position coordinate (128-bit fixed point), but that cannot be
passed in numeric form to Celestia:newposition. This value is handled
incorrectly in the constructor for class BigFix that takes a double in
version/src/celutil/bigfix.cpp.
]]
function vectorMetatable:toposition()
local a = {}
for c in std.xyz() do
local n = self[c]
if n == -2^63 then
table.insert(a, std.tourl("-9223372036854775808"))
elseif math.abs(n) < 2^63 then
table.insert(a, n)
else
error(string.format(
"Vector:toposition: %s coordinate in "
.. "(%.15g, %.15g, %.15g) too big or small to "
.. "convert",
c, self:getxyz()
))
end
end
return celestia:newposition(a[1], a[2], a[3])
end
--Return the angle in radians between two nonzero vectors.
function vectorMetatable:angle(v)
if type(v) ~= "userdata" or tostring(v) ~= "[Vector]" then
error("Vector:angle rejects non-vector " .. tostring(v))
end
local product = self:length() * v:length()
if product == 0 then
error(string.format(
"Vector:angle: vectors (%.15g, %.15g, %.15g), "
.. "(%.15g, %.15g, %.15g) are too short",
self:getx(), self:gety(), self:getz(),
v:getxyz()
))
end
local cosine = self * v / product
cosine = math.min( 1, cosine) --can be slightly greater than 1
cosine = math.max(-1, cosine)
return math.acos(cosine)
end
--[[
self is the forward vector.
If forward and up are nonzero and non-colinear, they define a plane.
Keep up in the plane, but make it a unit vector perpendicular to forward.
Rotate up less than 90 degrees from its original position.
]]
function vectorMetatable:erect(up)
if type(up) ~= "userdata" or tostring(up) ~= "[Vector]" then
error("Vector:erect rejects non-vector " .. tostring(up))
end
local n = self ^ up --n is perpendicular to self and up
local e = n ^ self --e lies in the same plane as self and up
if e:length() == 0 then
error(string.format(
"Vector:erect: (%.15g, %.15g, %.15g) and "
.. "(%.15g, %.15g, %.15g) do not define a plane",
self:getx(), self:gety(), self:getz(),
up:getxyz()
))
end
return e:normalize() --the new value for up
end
--Unary minus.
function vectorMetatable:__unm()
return -1 * self
end
function vectorMetatable:__div(divisor)
if type(divisor) ~= "number" then
error(string.format("vector (%.15g, %.15g, %.15g) "
.. "can't be divided by non-numeric %s",
self:getxyz(), tostring(divisor)))
end
if divisor == 0 then
error(string.format("vector (%.15g, %.15g, %.15g) "
.. "can't be divided by zero", self:getxyz()))
end
return self * (1 / divisor)
end
--Deduce the current version of Celestia from the metatables.
--Can't distinguish between 1.4.0 and 1.4.1; 1.5.0 and 1.5.1.
celestiaVersion = "1.3.1" --Celx introduced
if type(observerMetatable.cancelgoto) == "function" then
celestiaVersion = "1.3.2"
if type(celestiaMetatable.gettextwidth) == "function" then
celestiaVersion = "1.4.0" --or maybe 1.4.1
if type(celestiaMetatable.utctotdb) == "function" then
celestiaVersion = "1.5.0" --or maybe 1.5.1
if type(objectMetatable.addreferencemark) == "function"
then
celestiaVersion = "1.6.0"
if type(celestiaMetatable.seturl) == "function"
then
celestiaVersion = "1.6.1"
end
end
end
end
end
--The gl table for OpenGL.
--Constants taken from the header file GL/gl.h.
--gl already contains POINTS, LINES, LINE_LOOP, POLYGON, QUADS.
gl.LINE_STRIP = 3
--[[
When printing OpenGL text with Font:render, the first and third arguments of
glu.Ortho2D must be zero, and the amount of horizontal and vertcal translation
in effect with gl.Translate must be numbers that are 1/8 greater than an
integer. Otherwise, the left and bottom edges of the characters may be sliced
off.
gl.TexelRound returns its argument rounded to the closest number which is 1/8
greater than an integer. If tied, it rounds up (towards positive infinity).
]]
function gl.TexelRound(x)
if type(x) ~= "number" then
error("gl.TexelRound rejects non-numeric argument "
.. tostring(x))
end
local d = 1/8
return math.floor(x + 1/2 + d) + d
end
--Convert equatorial coordinates to universal.
radecRotation = celestia:newrotation(std.xaxis, std.tilt)
--[[
These functions return the field of view in radians that would be subtended by
the window when the user is 400 millimeters away.
See CelestiaCore::setFOVFromZoom.
width and height default to the window dimensions, but you'd want to supply a
different width and height if you called Observer:splitview and
Celestia:setwindowbordersvisible.
]]
function getverticalfov(width, height)
if width == nil and height == nil then
width, height = celestia:getscreendimension()
elseif type(width) ~= "number" or type(height) ~= "number" then
error("std.getverticalfov: requires numbers, not "
.. tostring(width) .. ", " .. tostring(height))
end
return 2 * math.atan2(std.mmPerIn * height, 2 * std.pixelsPerIn * 400)
end
function gethorizontalfov(width, height)
if width == nil and height == nil then
width, height = celestia:getscreendimension()
elseif type(width) ~= "number" or type(height) ~= "number" then
error("std.gethorizontalfov: requires numbers, not "
.. tostring(width) .. ", " .. tostring(height))
end
return 2 * math.atan2(std.mmPerIn * width, 2 * std.pixelsPerIn * 400)
end
--Round x to the nearest integer.
--If tied, round up (towards positive infinity).
function round(x)
if type(x) ~= "number" then
error("std.round rejects non-numeric " .. tostring(x))
end
return math.floor(.5 + x)
end
--Called by std.zero
local function signum(x)
if type(x) ~= "number" then
error("signum rejects " .. tostring(x))
end
if x > 0 then
return 1
end
if x < 0 then
return -1
end
return 0
end
--[[
Return a zero of the continuous function f between a and b,
i.e., a number t such that a <= t <= b and f(t) = 0.
a, b, and t will usually be TDB times.
The optional fourth argument is a table containing one or more terminating
conditions.
Each iteration halves the interval of uncertainty between a and b. Each
teration therefore doubles the precision of the answer, giving it one additional
correct bit. Our mantissa has only std.mantissa bits, so there's no reason to
iterate more than this number of times.
]]
function zero(f, a, b, terminate)
if type(f) ~= "function" then
error("std.zero rejects non-function " .. tostring(f))
end
if type(a) ~= "number" then
error("std.zero rejects non-numeric lower bound "
.. tostring(a))
end
if type(b) ~= "number" then
error("std.zero rejects non-numeric upper bound "
.. tostring(b))
end
if a >= b then
error(string.format(
"std.zero: a = %.15g must be < b = %.15g",
a, b
))
end
if terminate == nil then
terminate = {maxiter = std.mantissa}
else
if type(terminate) ~= "table" then
error("std.zero: optional 4th arg must be table, not "
.. tostring(terminate))
end
if type(terminate.maxiter) ~= "number"
and type(terminate.delta) ~= "number"
and type(terminate.epsilon) ~= "number" then
error("std.zero: table lacks maxiter, delta, epsilon")
end
if terminate.maxiter ~= nil then
if type(terminate.maxiter) ~= "number" then
error("std.zero rejects non-numeric "
.. "terminate.maxiter "
.. tostring(terminate.maxiter))
end
if terminate.maxiter > std.mantissa then
error(string.format(
"std.zero: terminate.maxiter %.15g "
.. "must be < std.mantissa %.15g",
terminate.maxiter, std.mantissa
))
end
end
if terminate.delta ~= nil
and type(terminate.delta) ~= "number" then
error("std.format rejects non-numeric terminate.delta "
.. tostring(terminate.delta))
end
if terminate.epsilon ~= nil
and type(terminate.epsilon) ~= "number" then
error("std.format rejects non-numeric "
.. "terminate.epsilon "
.. tostring(terminate.epsilon))
end
end
local fa = f(a)
if fa == 0 or terminate.epsilon and math.abs(fa) < terminate.epsilon
then
return a
end
local fb = f(b)
if fb == 0 or terminate.epsilon and math.abs(fb) < terminate.epsilon
then
return b
end
for i = 0, math.huge do
if signum(fa) == signum(fb) then
error(string.format("std.zero: f(%.15g) = %.15g "
.. "and f(%.15g) = %.15g have same sign",
a, f(a), b, f(b)
))
end
if terminate.delta and math.abs(a - b) < terminate.delta then
return a
end
local c = (a + b) / 2
if terminate.maxiter and i + 1 >= terminate.maxiter then
return c
end
local fc = f(c)
if terminate.epsilon
and math.abs(fc) < terminate.epsilon then
return c
end
--Halve the length of the interval (a, b).
if signum(fa) == signum(fc) then
a = c
fa = fc
else
b = c
fb = fc
end
end
end
--[[
Return four integers: x's sign bit (1 for negative, 0 for nonnegative), the
numerator and denominator of x's mantissa (both positive), and x's exponent.
For example, if x == 1/3 and std.mantissa == 53, then return
0, 6004799503160661, 9007199254740992, -1,
where 9007199254740992 == 2^std.mantissa.
]]
function fraction(x)
if type(x) ~= "number" then
error("std.fraction rejects non-numeric " .. tostring(x))
end
if x == 0 or math.abs(x) == math.huge then
error(string.format("std.fraction rejects out-of-range %.15g",
x))
end
local sign = 0
if x < 0 then
sign = 1
end
local mantissa, exponent = math.frexp(x)
return {
sign = sign,
numerator = math.abs(mantissa) * denominator,
denominator = 2^std.mantissa,
exponent = exponent
}
end
--[[
Return the next number, i.e., the smallest number that is bigger than x.
For example, assuming std.mantissa == 53,
if x == 1 == (2^52 / 2^53) * 2^1, return (2^52 + 1) / 2^53) * 2^1;
if x == ((2^53 - 1) / 2^53) * 2^1, return (2^52 / 2^53) * 2^2.
Do not confuse this function with the Lua function next.
]]
--minimum and maximum double exponents, from the C header file float.h
local dblMinExp = -1021
local dblMaxExp = 1024
--smallest and largest positive numbers that are not denormalized
local smallest = (1/2) * 2^dblMinExp
local largest = (2^std.mantissa - 1) * 2^(dblMaxExp - std.mantissa)
function next(x)
if type(x) ~= "number" then
error("std.next rejects non-numeric " .. tostring(x))
end
if x == -math.huge then
return -largest
end
if x < -smallest then
--x is negative and not denormalized.
local frac = std.fraction(x)
if frac.numerator > 2^(std.mantissa - 1) then
return -((frac.numerator - 1) / frac.denominator)
* 2^frac.exponent
end
return -((2^std.mantissa - 1) / frac.denominator)
* 2^(frac.exponent - 1)
end
if x < smallest then
--x is 0 or denormalized.
--Add the smallest positive denormalized number.
return x + 2^(dblMinExp - std.mantissa)
end
if x < largest then
--x is positive and not denormalized.
local frac = std.fraction(x)
if frac.numerator < 2^std.mantissa - 1 then
return ((frac.numerator + 1) / frac.denominator)
* 2^frac.exponent
end
return (2^(std.mantissa - 1) / frac.denominator)
* 2^(frac.exponent + 1)
end
if x == largest then
return math.huge
end
if x == math.huge then
error(string.format("std.next: no number comes after %.15g", x))
end
error(string.format("std.next: unknown number %.15g", x))
end
--[[
Return the previous number, i.e., the biggest number that is smaller than x.
For example, assuming std.mantissa == 53,
if x == 1 == (2^52 / 2^53) * 2^1, return (2^53 - 1) / 2^53) * 2^0.
]]
function prev(x)
if type(x) ~= "number" then
error("std.prev rejects non-numeric " .. tostring(x))
end
if x == -math.huge then
error(string.format("std.prev: no number comes before %.15g",
x))
end
if x <= -smallest then
--x is negative and not denormalized.
local frac = std.fraction(x)
if frac.numerator < 2^std.mantissa - 1 then
return -((frac.numerator + 1) / frac.denominator)
* 2^frac.exponent
end
return -((2^(std.mantissa - 1)) / frac.denominator)
* 2^(frac.exponent + 1)
end
if x <= smallest then
--x is 0 or denormalized.
--Subtract the smallest positive denormalized number.
return x - 2^(DBL_MIN_EXP - std.mantissa)
end
if x <= largest then
--x is positive and not denormalized.
local frac = std.fraction(x)
if frac.numerator > 2^(std.mantissa - 1) then
return ((frac.numerator - 1) / frac.denominator)
* 2^frac.exponent
end
return ((2^std.mantissa - 1) / frac.denominator)
* 2^(frac.exponent - 1)
end
if x == math.huge then
return largest
end
error(string.format("std.prev: unknown number %.15g", x))
end
--[[
Return an iterator that iterates through the consecutive 2 * n + 1 real numbers
centered at x, in increasing order.
]]
function consecutive(x, n)
local xend = x
for j = 0, n do
x = std.prev(x)
xend = std.next(xend)
end
local i = -n - 1
return function()
x = std.next(x)
i = i + 1
if x == xend then
return nil, nil
end
return i, x
end
end
--[[
Change the Unicode code number of a character into a string consisting of that
character.
Break the Unicode number into UTF-8 bytes and paste them back together
with string.char.
2^6 represents 2 to the 6th power == 64. When dividing a number by 64, the
quotient (producted by the operator /) will be the original number with the six
rightmost bits removed. The remainder (produced by the operator %) will be the
original number with all but the six rightmost bits removed. Together, these
operators let us dismantle a Unicode number into groups of 6 bits each. The
operators have equal precedence and associativity.
]]
function utf8(unicode)
if type(unicode) ~= "number" then
error("std.utf8 rejects non-numeric " .. tostring(unicode))
end
if unicode < 0x0 then
error(string.format("std.utf8 rejects negative number %.15g",
unicode))
end
if unicode ~= math.floor(unicode) then
error(string.format("std.utf8 rejects non-integer %.15g",
unicode))
end
if unicode <= 0x007F then
return string.char(unicode)
end
if unicode <= 0x07FF then
return string.char(
0xC0 + math.floor(unicode / 2^6),
0x80 + unicode % 2^6)
end
if unicode <= 0xFFFF then
return string.char(
0xE0 + math.floor(unicode / 2^12),
0x80 + math.floor(unicode / 2^6 % 2^6),
0x80 + unicode % 2^6)
end
if unicode <= 0x1FFFFF then
return string.char(
0xF0 + math.floor(unicode / 2^18),
0x80 + math.floor(unicode / 2^12 % 2^6),
0x80 + math.floor(unicode / 2^6 % 2^6),
0x80 + unicode % 2^6)
end
if unicode <= 0x3FFFFFF then
return string.char(
0xF8 + math.floor(unicode / 2^24),
0x80 + math.floor(unicode / 2^18 % 2^6),
0x80 + math.floor(unicode / 2^12 % 2^6),
0x80 + math.floor(unicode / 2^6 % 2^6),
0x80 + unicode % 2^6)
end
if unicode <= 0x7FFFFFFF then
return string.char(
0xFC + math.floor(unicode / 2^30),
0x80 + math.floor(unicode / 2^24 % 2^6),
0x80 + math.floor(unicode / 2^18 % 2^6),
0x80 + math.floor(unicode / 2^12 % 2^6),
0x80 + math.floor(unicode / 2^6 % 2^6),
0x80 + unicode % 2^6)
end
error(string.format("std.utf8: character code %.0f (decimal) too big",
unicode))
end
--Special characters. Planets, asteroids, and zodiac missing in some fonts.
char = {
degree = std.utf8(0x00B0),
minute = std.utf8(0x2032),
second = std.utf8(0x2033),
minus = std.utf8(0x2212),
middot = std.utf8(0x00B7), --dot product
times = std.utf8(0x00D7), --multiply; also means "by"
cross = std.utf8(0x00D7), --cross product of two vectors
ndash = std.utf8(0x2013), --en dash
--quotation marks, named after HTML character entities
lsquo = std.utf8(0x2018), --left single
rsquo = std.utf8(0x2019), --right single
ldquo = std.utf8(0x201C), --left double
rdquo = std.utf8(0x201D), --right double
--arrows, named after HTML character entities
larr = std.utf8(0x2190), --left
uarr = std.utf8(0x2191), --up
rarr = std.utf8(0x2192), --right
darr = std.utf8(0x2193), --down
--funny letters
aelig = std.utf8(0x00E6), --ligature for genitive constellations
ouml = std.utf8(0x00F6), --diaeresis (separate syllable): Bootes
l = std.utf8(0x2113), --script lowercase L for galactic latitude
--lowercase Greek letters for Bayer designation of stars
alpha = std.utf8(0x03B1),
beta = std.utf8(0x03B2),
gamma = std.utf8(0x03B3),
delta = std.utf8(0x03B4),
epsilon = std.utf8(0x03B5),
zeta = std.utf8(0x03B6),
eta = std.utf8(0x03B7),
theta = std.utf8(0x03B8),
iota = std.utf8(0x03B9),
kappa = std.utf8(0x03BA),
lambda = std.utf8(0x03BB),
mu = std.utf8(0x03BC),
nu = std.utf8(0x03BD),
xi = std.utf8(0x03BE),
omicron = std.utf8(0x03BF),
pi = std.utf8(0x03C0),
rho = std.utf8(0x03C1),
sigma = std.utf8(0x03C3), --not the final sigma
tau = std.utf8(0x03C4),
upsilon = std.utf8(0x03C5),
phi = std.utf8(0x03C6),
chi = std.utf8(0x03C7),
psi = std.utf8(0x03C8),
omega = std.utf8(0x03C9),
sun = std.utf8(0x2609),
mercury = std.utf8(0x263F), --planets of the Solar System
venus = std.utf8(0x2640),
earth = std.utf8(0x2641),
mars = std.utf8(0x2642),
jupiter = std.utf8(0x2643),
saturn = std.utf8(0x2644),
uranus = std.utf8(0x2645),
neptune = std.utf8(0x2646),
pluto = std.utf8(0x2647),
ceres = std.utf8(0x26B3), --asteroids
pallas = std.utf8(0x26B4),
juno = std.utf8(0x26B5),
vesta = std.utf8(0x26B6),
aries = std.utf8(0x2648), --constellations of the zodiac
taurus = std.utf8(0x2649),
gemini = std.utf8(0x264A),
cancer = std.utf8(0x264B),
leo = std.utf8(0x264C),
virgo = std.utf8(0x264D),
libra = std.utf8(0x264E),
scorpius = std.utf8(0x264F),
sagittarius = std.utf8(0x2650),
capricorn = std.utf8(0x2651), --Unicode char is not named capricornus
aquarius = std.utf8(0x2652),
pisces = std.utf8(0x2653)
}
--[[
Instead of hardcoding the month and day names into the Celx Standard Library,
we could have gotten them by saying
--Get the name of "January".
local t = os.time({year = 2000, month = 1, day = 1})
local name = os.date("%B", t)
And they would have been locale-specific, too. But this would have required the
library to call celestia:requestsystemaccess.
]]
monthName = {
"January", --key is 1
"February",
"March",
"April",
"May",
"June",
"July",
"August",
"September",
"October",
"November",
"December" --key is 12
}
--Start with Monday because January 1, 4713 B.C. (the first Julian date)
--would have been a Monday if our calendar went back that far.
dayName = {
"Monday", --key is 1
"Tuesday",
"Wednesday",
"Thursday",
"Friday",
"Saturday",
"Sunday" --key is 7
}
zodiac = {
"Aries", --key is 1
"Taurus",
"Gemini",
"Cancer",
"Leo",
"Virgo",
"Libra",
"Scorpius",
"Sagittarius",
"Capricornus",
"Aquarius",
"Pisces" --key is 12
}
--[[
88 constellation names from version/src/celengine/constellation.cpp.
There's only 88 because Serpens is not divided into Serpens Caput and
Serpens Cauda.
The three columns are the nominative case, genitive case (for Bayer and
Flamsteed designations), and abbreviation.
Trailing ae in the genitive case can be written with a ligature:
"Urs" .. std.char.aelig
Bootes can be written "Bo" .. std.char.ouml .. "tes".
The non-Latin names are in the .po files.
]]
constellations = {
{"Andromeda", "Andromedae", "And"},
{"Antlia", "Antliae", "Ant"},
{"Apus", "Apodis", "Aps"},
{"Aquarius", "Aquarii", "Aqr"},
{"Aquila", "Aquilae", "Aql"},
{"Ara", "Arae", "Ara"},
{"Aries", "Arietis", "Ari"},
{"Auriga", "Aurigae", "Aur"},
{"Bootes", "Bootis", "Boo"},
{"Caelum", "Caeli", "Cae"},
{"Camelopardalis", "Camelopardalis", "Cam"},
{"Cancer", "Cancri", "Cnc"},
{"Canes Venatici", "Canum Venaticorum", "CVn"},
{"Canis Major", "Canis Majoris", "CMa"},
{"Canis Minor", "Canis Minoris", "CMi"},
{"Capricornus", "Capricorni", "Cap"},
{"Carina", "Carinae", "Car"},
{"Cassiopeia", "Cassiopeiae", "Cas"},
{"Centaurus", "Centauri", "Cen"},
{"Cepheus", "Cephei", "Cep"},
{"Cetus", "Ceti", "Cet"},
{"Chamaeleon", "Chamaeleontis", "Cha"},
{"Circinus", "Circini", "Cir"},
{"Columba", "Columbae", "Col"},
{"Coma Berenices", "Comae Berenices", "Com"},
{"Corona Australis", "Coronae Australis", "CrA"},
{"Corona Borealis", "Coronae Borealis", "CrB"},
{"Corvus", "Corvi", "Crv"},
{"Crater", "Crateris", "Crt"},
{"Crux", "Crucis", "Cru"},
{"Cygnus", "Cygni", "Cyg"},
{"Delphinus", "Delphini", "Del"},
{"Dorado", "Doradus", "Dor"},
{"Draco", "Draconis", "Dra"},
{"Equuleus", "Equulei", "Equ"},
{"Eridanus", "Eridani", "Eri"},
{"Fornax", "Fornacis", "For"},
{"Gemini", "Geminorum", "Gem"},
{"Grus", "Gruis", "Gru"},
{"Hercules", "Herculis", "Her"},
{"Horologium", "Horologii", "Hor"},
{"Hydra", "Hydrae", "Hya"},
{"Hydrus", "Hydri", "Hyi"},
{"Indus", "Indi", "Ind"},
{"Lacerta", "Lacertae", "Lac"},
{"Leo Minor", "Leonis Minoris", "LMi"},
{"Leo", "Leonis", "Leo"},
{"Lepus", "Leporis", "Lep"},
{"Libra", "Librae", "Lib"},
{"Lupus", "Lupi", "Lup"},
{"Lynx", "Lyncis", "Lyn"},
{"Lyra", "Lyrae", "Lyr"},
{"Mensa", "Mensae", "Men"},
{"Microscopium", "Microscopii", "Mic"},
{"Monoceros", "Monocerotis", "Mon"},
{"Musca", "Muscae", "Mus"},
{"Norma", "Normae", "Nor"},
{"Octans", "Octantis", "Oct"},
{"Ophiuchus", "Ophiuchi", "Oph"},
{"Orion", "Orionis", "Ori"},
{"Pavo", "Pavonis", "Pav"},
{"Pegasus", "Pegasi", "Peg"},
{"Perseus", "Persei", "Per"},
{"Phoenix", "Phoenicis", "Phe"},
{"Pictor", "Pictoris", "Pic"},
{"Pisces", "Piscium", "Psc"},
{"Piscis Austrinus", "Piscis Austrini", "PsA"},
{"Puppis", "Puppis", "Pup"},
{"Pyxis", "Pyxidis", "Pyx"},
{"Reticulum", "Reticuli", "Ret"},
{"Sagitta", "Sagittae", "Sge"},
{"Sagittarius", "Sagittarii", "Sgr"},
{"Scorpius", "Scorpii", "Sco"},
{"Sculptor", "Sculptoris", "Scl"},
{"Scutum", "Scuti", "Sct"},
{"Serpens", "Serpentis", "Ser"},
{"Sextans", "Sextantis", "Sex"},
{"Taurus", "Tauri", "Tau"},
{"Telescopium", "Telescopii", "Tel"},
{"Triangulum Australe", "Trianguli Australis", "TrA"},
{"Triangulum", "Trianguli", "Tri"},
{"Tucana", "Tucanae", "Tuc"},
{"Ursa Major", "Ursae Majoris", "UMa"},
{"Ursa Minor", "Ursae Minoris", "UMi"},
{"Vela", "Velorum", "Vel"},
{"Virgo", "Virginis", "Vir"},
{"Volans", "Volantis", "Vol"},
{"Vulpecula", "Vulpeculae", "Vul"}
}
--[[
When t == starttime, returns startval.
When t == endtime, returns endval.
When t is in between, it returns a value between startval and endval,
increasing or decreasing gradually with no sudden start or stop.
]]
function spline(t, startTime, endTime, startVal, endVal, f)
if type(t) ~= "number" then
error("std.spline rejects non-numeric time " .. tostring(t))
end
if type(startTime) ~= "number" then
error("std.spline rejects non-numeric start time "
.. tostring(startTime))
end
if type(endTime) ~= "number" then
error("std.spline rejects non-numeric end time "
.. tostring(endTime))
end
if type(startVal) ~= "number" then
error("std.spline rejects non-numeric start value "
.. tostring(startVal))
end
if type(endVal) ~= "number" then
error("std.spline rejects non-numeric end value "
.. tostring(endVal))
end
if t < startTime then
error(string.format(
"std.spline: time %.15g must be >= start time %.15g",
t, startTime))
end
if t > endTime then
error(string.format(
"std.spline: time %.15g must be <= end time %.15g",
t, endTime))
end
if startTime == endTime then
return endVal
end
if f == nil then
--value at 0 is 0, at 1 is 1.
--derivative at 0 is 0, at 1 is 0.
f = function(x) return (3 - 2 * x) * x * x end
elseif type(f) ~= "function" then
error("std.spline rejects non-function " .. type(f) .. " "
.. tostring(f))
end
local fraction = (t - startTime) / (endTime - startTime) --in [0, 1]
return startVal + (endVal - startVal) * f(fraction)
end
--[[
Convert latitude (or altitude) from radians to degrees, minutes, seconds.
theta is positive for north, negative for south.
]]
function tolat(theta)
if type(theta) ~= "number" then
error("std.tolat rejects non-numeric " .. tostring(theta))
end
if math.abs(theta) > math.pi/2 then
error(string.format("std.tolat: absolute value of argument "
.. "%.15g must be <= pi/2", theta))
end
local signum = 0
if theta > 0 then
signum = 1 --north
elseif theta < 0 then
signum = -1 --south
end
local d = math.deg(math.abs(theta))
local m = 60 * math.fmod(d, 1) --math.fmod returns fractional part of d
return {
signum = signum,
degrees = math.floor(d), --math.floor returns integral part of d
minutes = math.floor(m),
seconds = 60 * math.fmod(m, 1)
}
end
--[[
Convert longitude from radians to degrees, minutes, seconds. theta is positive
for east, negative for west, and zero for on the prime meridian.
The result lies in the range 180 degrees West < result <= 180 degrees East.
]]
function tolong(theta)
if type(theta) ~= "number" then
error("std.tolong rejects non-numeric " .. tostring(theta))
end
--d is in the range -360 < d < 360.
local d = math.fmod(math.deg(theta), 360)
--Reduce d to the range -180 < d <= 180.
if d <= -180 then
d = d + 360
elseif d > 180 then
d = d - 360
end
local signum = 0
if d > 0 then
signum = 1 --east
elseif d < 0 then
signum = -1 --west
end
d = math.abs(d)
local m = 60 * math.fmod(d, 1) --math.fmod returns fractional part of d
return {
signum = signum,
degrees = math.floor(d), --math.floor returns integral part of d
minutes = math.floor(m),
seconds = 60 * math.fmod(m, 1)
}
end
--[[
Convert azimuth from radians to degrees, minutes, seconds.
theta is the angle to the right from due north.
]]
function toaz(theta)
if type(theta) ~= "number" then
error("std.toaz rejects non-numeric " .. tostring(theta))
end
--d is in the range -360 < d < 360.
local d = math.fmod(math.deg(theta), 360)
--Reduce d to the range 0 <= d < 360.
if d < 0 then
d = d + 360
--If the original d was a tiny negative fraction,
--the above addition might result in 360.
if d >= 360 then
d = d - 360
end
end
local m = 60 * math.fmod(d, 1) --math.fmod returns fractional part of d
return {
degrees = math.floor(d), --math.floor return integral part of d
minutes = math.floor(m),
seconds = 60 * math.fmod(m, 1)
}
end
--[[
Break d days into days, hours, minutes, seconds.
days, hours, and minutes are whole numbers.
math.floor(x) returns the integral part of x;
math.fmod(x, 1) returns the fractional part.
For example, math.floor(2.5) returns 2; math.fmod(2.5, 1) returns .5.
]]
function todhms(d)
if type(d) ~= "number" or d < 0 then
error("std.todhms requires nonnegative number, not "
.. tostring(d))
end
local h = 24 * math.fmod(d, 1)
local m = 60 * math.fmod(h, 1)
return {
days = math.floor(d),
hours = math.floor(h),
minutes = math.floor(m),
seconds = 60 * math.fmod(m, 1)
}
end
--[[
Convert right ascension in radians to hours, minutes, seconds.
1 hour of RA = 360/24 degrees of arc = 15 degrees of arc
1 minute of RA = 360/(24*60) degrees of arc = 15 minutes of arc
1 second of RA = 360/(24*60*60) degrees of arc = 15 seconds of arc
]]
function tora(theta)
if type(theta) ~= "number" then
error("std.tora rejects non-numeric " .. tostring(theta))
end
if theta < 0 or theta >= 2 * math.pi then
error(string.format(
"std.tora: argument %.15g must be >= 0 and < 2pi",
theta))
end
local h = math.deg(theta) * 24 / 360
local m = 60 * math.fmod(h, 1)
return {
hours = math.floor(h),
minutes = math.floor(m),
seconds = 60 * math.fmod(m, 1)
}
end
--Convert declination in radians to degrees, minutes, seconds.
function todec(theta)
if type(theta) ~= "number" then
error("std.todec rejects non-numeric " .. tostring(theta))
end
if math.abs(theta) > math.pi / 2 then
error(string.format("std.todec: absolute value of argument "
.. "%.15g must be <= pi/2", theta))
end
local signum = 0
if theta > 0 then
signum = 1
elseif theta < 0 then
signum = -1
end
local d = math.deg(math.abs(theta))
local m = 60 * math.fmod(d, 1)
return {
signum = signum,
degrees = math.floor(d),
minutes = math.floor(m),
seconds = 60 * math.fmod(m, 1)
}
end
--for printing the sign of a declination
function sign(x)
if type(x) ~= "number" then
error("std.sign rejects non-numeric " .. tostring(x))
end
if x > 0 then
return "+"
end
if x < 0 then
return "-"
end
return ""
end
http://www.donandcarla.com/Celestia/cel_scripting/guide/Cel_Script_Guide_v1_0g.htm
and
http://en.wikibooks.org/wiki/Celestia/Cel_Scripting.
http://celestia.h-schmidt.net/celx-summary-latest.html
and
http://en.wikibooks.org/wiki/Celestia/Celx_Scripting.
http://www.lua.org/manual/5.2/.
It’s short and dense,
and slightly different than 5.1.
The first edition of
Programming In Lua
by the creator of the language,
Roberto Ierusalimschy,
is at
http://www.lua.org/pil/contents.html.
It’s bigger and easier to read, but covers only Lua 5.0.
beginDate
and
endDate
of scripted orbit.
Celestia:utctotdb
current date
Celestia:geturl
has current date.Observer:gettime
has current date.std.zero
has the current year.context.stroke();
after the
for
loop.
context.stroke();
top → topper.CODE
font?
No.
on Chrome screen.screencapture -l<windowid>?
Also in appendix for
Celestia:takescreenshot.
Will
Celestia:takescreenshot
work on Mac compiled from source code?
/Applications/Celestia.app,
not
/Applications/Celestia/Celestia.app.
~/Library/Application Support/CelestiaResources.
This might eliminate the need to make the application’s
CelestiaResouces
directory read/write.
Unfortunately, it did not work for me.
I had the best results when I saved Celx scripts to my Documents folder.
Celestia had no problems finding them there,
provided they had the
.celx
extension.std.c,
std.G.